5.2运动的合成与分解 自主提升过关练(word版含答案)
文档属性
| 名称 | 5.2运动的合成与分解 自主提升过关练(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 473.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-19 02:04:22 | ||
图片预览




文档简介
5.2运动的合成与分解 自主提升过关练(解析版)
一、选择题
1.船在静水中的速度与时间的关系如图甲所示,河水的流速与离某一河岸距离的关系如图乙所示。已知两岸相互平行,若要使船以最短时间渡河(河宽为400m),则( )
A.船渡河的最短时间为80s
B.船在河水中的最大速度是5m/s
C.船渡河的位移为500m
D.船在行驶过程中船头必须与河岸垂直
2.关于不共线的两个直线运动的合运动的描述正确的是( )
A.两个匀速直线运动的合运动可能是曲线运动
B.一个匀速直线运动和一个匀加速直线运动的合运动一定是匀变速曲线运动
C.两个匀加速直线的合运动一定是匀加速直线运动
D.两个匀加速直线运动的合运动可能是直线运动也可能是曲线运动
3.甲、乙两船在同一河流中同时开始渡河,河水流速为,船在静水中的速率均为,甲、乙两船船头均与河岸成角,如图,已知甲船恰能垂直到达河正对岸的A点,乙船到达河对岸的点,之间的距离为,则正确的( )
A.若仅是河水流速增大,则两船的渡河时间都不变
B.乙船先到达对岸
C.不论河水流速如何改变,只要适当改变角,甲船总能到达正对岸的点
D.若仅是河水流速增大,则两船到达对岸时,两船之间的距离仍然为
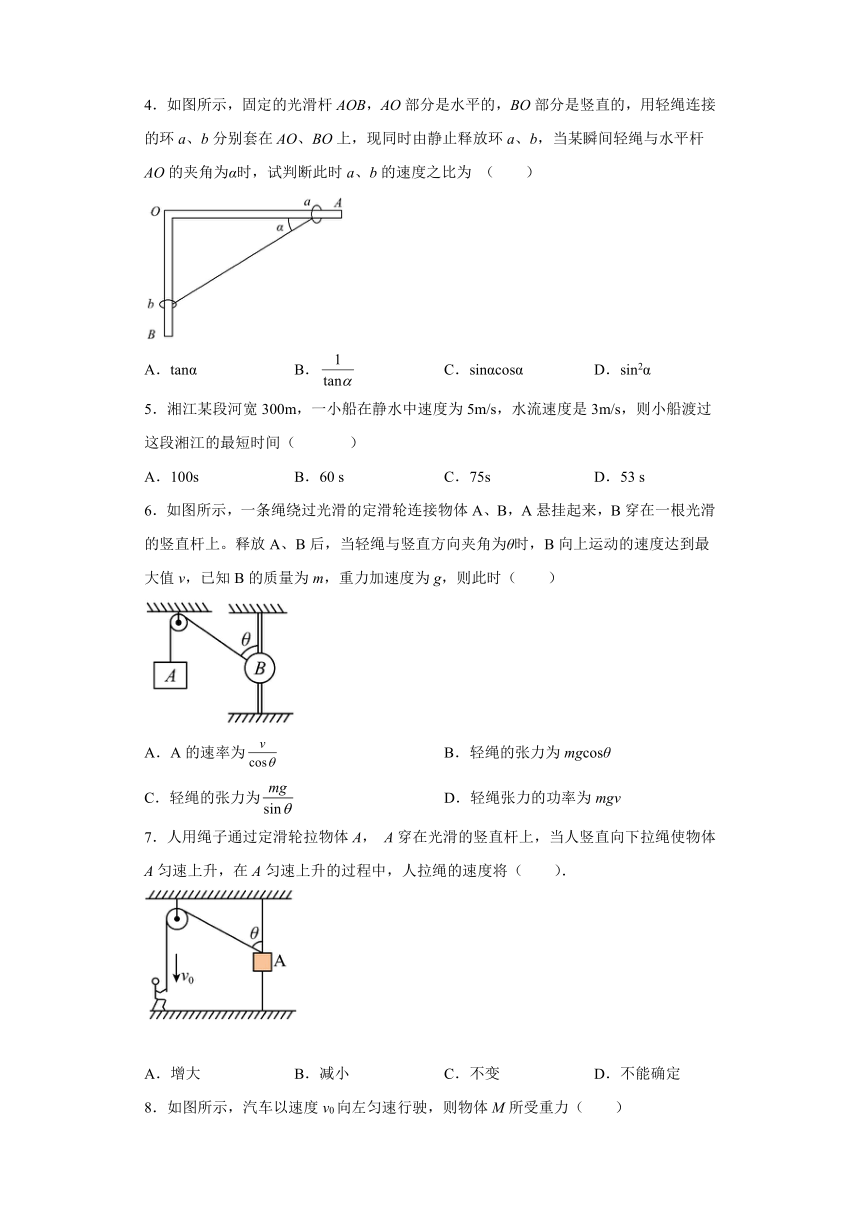
4.如图所示,固定的光滑杆AOB,AO部分是水平的,BO部分是竖直的,用轻绳连接的环a、b分别套在AO、BO上,现同时由静止释放环a、b,当某瞬间轻绳与水平杆AO的夹角为α时,试判断此时a、b的速度之比为 ( )
A.tanα B. C.sinαcosα D.sin2α
5.湘江某段河宽300m,一小船在静水中速度为5m/s,水流速度是3m/s,则小船渡过这段湘江的最短时间( )
A.100s B.60 s C.75s D.53 s
6.如图所示,一条绳绕过光滑的定滑轮连接物体A、B,A悬挂起来,B穿在一根光滑的竖直杆上。释放A、B后,当轻绳与竖直方向夹角为θ时,B向上运动的速度达到最大值v,已知B的质量为m,重力加速度为g,则此时( )
A.A的速率为 B.轻绳的张力为mgcosθ
C.轻绳的张力为 D.轻绳张力的功率为mgv
7.人用绳子通过定滑轮拉物体A, A穿在光滑的竖直杆上,当人竖直向下拉绳使物体A匀速上升,在A匀速上升的过程中,人拉绳的速度将( ).
A.增大 B.减小 C.不变 D.不能确定
8.如图所示,汽车以速度v0向左匀速行驶,则物体M所受重力( )
A.等于绳的拉力
B.大于绳的拉力
C.小于绳的拉力
D.条件不足,无法判定
9.2021年10月29日,华南师大附中校运会开幕式隆重举行,各班进行入场式表演时,无人机从地面开始起飞,在空中进行跟踪拍摄。若无人机在水平和竖直方向运动的速度随时间变化关系图像如图所示,则无人机( )
A.在的时间内,运动轨迹为曲线 B.在的时间内,运动轨迹为直线
C.在的时间内,速度均匀变化 D.在时刻的加速度方向竖直向上
10.如图所示,有一条宽为的河道,一小船从岸边的某点渡河,渡河过程中保持船头指向与河岸始终垂直。已知小船在静水中的速度大小为,水流速度大小为。下列说法正确的是( )
A.小船渡河过程中的位移大小为
B.小船渡河的时间是
C.小船在河水中航行的轨迹是曲线
D.小船在河水中的速度是
11.质量为2 kg的质点在直角坐标系xOy平面内做曲线运动,在x轴方向的速度—时间图像和y轴方向的位移—时间图像分别如图甲、乙所示,下列说法正确的是( )
A.质点的初速度大小为4 m/s
B.质点所受的合外力大小为4 N
C.质点初速度的方向与合外力方向垂直
D.2 s末质点速度大小为8 m/s
12.一小船渡河,河宽d=180m,水流的速度v1=5m/s,小船在静水中的速度v2=4m/s,下列说法正确的是( )
A.小船能垂直河岸渡过此河,位移大小为180m
B.小船渡河过程中保持船头方向不变,若水流速度变大,则渡河时间将变短
C.调整好船头方向且保持不变,小船渡河所用的时间可能为40s
D.调整好船头方向且保持不变,小船渡河的最小位移为225m
13.一个物体同时参与不在同一直线上的一个初速度为零的匀加速直线运动和一个匀速直线运动,它的合运动的轨迹是( )
A.直线 B.双曲线 C.抛物线 D.其他曲线
14.如图所示,粗糙的水平传送带的运行速度大小为v,一物块以从传送带的边缘垂直传送带运行方向滑上传送带。在物块达到与传送带共速前的过程中,下列说法正确的是( )
A.物块的速度一直增大 B.物块的速度一直减小
C.物块可能做直线运动 D.物块一定做曲线运动
15.在河面上方20m的岸上有人用长绳栓住一条小船,开始时绳与水面的夹角为30°。人以恒定的速率v=3m/s拉绳,使小船靠岸,那么( )
A.5s时绳与水面的夹角为60°
B.5s内小船前进了15m
C.5s时小船的速率为3.75m/s
D.5s时小船距离岸边15m
二、解答题
16.一艘小船在宽的河中横渡到对岸,已知水流速度,小船在静水中的速度,,,求:
(1)船渡河最短的时间,最短时间渡河船的位移;
(2)船过河位移最小时,船头与河岸间的夹角。
17.光滑水平面上,一个质量为2kg的物体从静止开始运动,在前5s受到一个沿正东方向、大小为4N的水平恒力作用;从第5s末开始改为受到正北方向、大小为2N的水平恒力作用了10s,求:
(1)物体在15s内的位移;
(2)物体在15s末的速度。
参考答案
1.BD
【详解】
AD.在行驶过程中船头与河岸垂直,指向正对岸时,渡河时间最短,且最短时间为
A错误,D正确;
B.船运动到河中央时,速度最大,且最大速度为
B正确;
C.从岸边运动到河中间的过程中,河水的流速与到岸边的距离成正比,而垂直河岸方向上,船匀速运动,即船到岸边的距离与时间成正比,可分析得出:船顺水漂流的速度与时间成正比,因此在前半程,沿河岸平均速度
同理后半程沿河岸的平均速度也相同,因此沿河运动的位移
可得船的总位移
C错误。
故选BD。
2.BD
【详解】
A.两个匀速直线运动的合运动是匀速直线运动,故A错误;
B.一个匀速直线运动和一个匀加速直线运动的合运动,由于不共线,则合外力大小不变,与速度方向不共线,则一定是匀变速曲线运动,故B正确;
CD.两个匀加速直线的合运动,由于不共线,则合外力大小不变,但合外力与速度方向关系未知,不一定是匀加速直线运动,可能是直线运动也可能是曲线运动,故C错误,D正确。
故选BD。
3.AD
【详解】
AB.将小船的运动分解为平行于河岸和垂直于河岸两个方向,抓住分运动和合运动具有等时性,知甲乙两船到达对岸的时间相等。渡河的时间
与河水流速v0无关。则增大v0,两船的渡河时间都不变,故B错误,A正确;
C.只有甲船速度大于水流速度时,不论水流速v0如何改变,只要适当改变θ角,甲船都可能到达河的正对岸A点,故C错误;
D.若仅是河水流速v0增大,则两船到达对岸时间不变,根据速度的分解,船在水平方向的分速度仍不变,则两船之间的距离
两船之间的距离和河水流速v0无关,大小不变,故D正确。
故选AD。
4.A
【详解】
根据速度的分解可知
则a、b的速度之比为
故选A。
5.B
【详解】
渡河的最短时间只与河宽和船速有关,当船头垂直渡河时时间最短,最短时间为
故选B。
6.D
【详解】
A.物体A、B沿绳方向的速度相等,则有
故A错误;
BC.B向上运动的速度达到最大值时,对于B,绳拉力的竖直分力与重力平衡,则有
解得
故BC错误;
D.轻绳张力的功率为B克服重力做功的功率,即为
故D正确。
故选D。
7.B
【详解】
由速度的分解可知
在A匀速上升的过程中,θ角变大,则人拉绳的速度将减小。
故选B。
8.C
【详解】
汽车参与两个分运动,即沿绳子拉伸方向和垂直绳子方向(绕滑轮转动)的两个分运动,如图所示
将汽车合速度v0正交分解,可知物体上升速度等于汽车沿绳子拉伸方向的分速度,即
汽车向左匀速运动,v0不变,θ越来越小,则越来越大,所以物体上升的速度v越来越大,即物体向上做加速运动,根据牛顿第二定律可知,轻绳的拉力大于物体受的重力。
故选C。
9.C
【详解】
A.在的时间内,无人机沿x方向和y方向均做初速度为零的匀加速度直线运动,其合运动仍是直线运动,故A错误;
B.在的时间内,无人机的加速度沿y轴负向,但初速度为时刻的末速度,方向不是沿y轴方向,初速度和加速度不共线,因此运动轨迹应是曲线,故B错误;
C.在的时间内,无人机加速度沿y轴负向,且为定值,因此其速度均匀变化,故C正确;
D.在时刻,无人机有x轴负方向和y轴正方向的加速度分量,合加速度方向不是竖直向上,故D错误。
故选C。
10.B
【详解】
A.小船参与了两个方向的运动,一个是垂直于河岸的运动,一个是沿着河岸的运动,小船到达河对岸时,垂直于河岸的位移为,总位移大于,A错误;
B.由于渡河过程中保持船头指向与河岸始终垂直,故
解得
选项B正确;
C.小船垂直于河岸方向做匀速直线运动,沿河岸方向也做匀速直线运动,所以小船的实际运动为匀速直线运动,C错误;
D.小船在河水中的速度为
D错误。
故选B。
11.B
【详解】
AD.x方向的初速度为4m/s,y方向做匀速直线运动,其速度为4m/s,质点的初速度
为
2s末速度为
AD错误;
B.y方向的加速度为0,x方向的加速度为
由牛顿第二定律可得
B正确;
C.由于只有x方向有加速度,所以合外力与x方向同向,而初速度与x方向不垂直,所以质点初速度的方向与合外力方向不垂直,C错误。
故选B。
12.D
【详解】
A.由于小船在静水中的速度v2=4m/s小于水流速度v1=5m/s,小船不能垂直河岸渡过此河,故A错误;
B.若保持船头方向不变,水流速度变大,垂直河岸方向的分运动速度不变,则渡河时间不变,故B错误;
CD.当小船在静水中的速度与河岸垂直,渡河时间最短,则最短时间为
故小船渡河所用的时间不可能为40s,故C错误;
D.由于小船在静水中的速度v2=4m/s小于水流速度v1=5m/s,则当合速度垂直于船速时,航程最短,有
故D正确。
故选D。
13.C
【详解】
不在同一直线上的匀加速直线运动和匀速直线运动合成时,只有一个方向有加速度,合加速度的方向就在该方向上,与合速度的方向不在同一直线上,因此合运动是曲线运动,即为抛物线。
故选C。
14.D
【详解】
AB.物块在沿着传送带的方向做匀加速直线运动,即由0加到v,在垂直传动带速度方向做匀减速直线运动,即由v0减到0,所以速度的大小由v0变到v,若,则物块速度先减小后增大,若,则速度一直减小,故AB错误;
CD.由上分析可知,物块受到的摩擦力有两个效果,一个是垂直传送带方向让物块减速,加一个是沿传送带方向让物块加速,故最终的摩擦力方向与初速度的方向存在夹角,不在同一直线上,故物块一定做曲线运动,故D正确,C错误。
故选D。
15.D
【详解】
开始时滑轮与船之间的绳长为
船头到河岸的距离为
5s时滑轮与船之间的绳长为
船头到河岸的距离为
5s内小船前进了
此时绳与水面的夹角θ的余弦值为
即θ不等于60°。
5s时小船的速率为
综上所述可知ABC错误,D正确。
故选D。
16.(1),;(2),指向上游
【详解】
(1)船渡河时,保持船头方向与河岸垂直时,渡河时间最短,有
最短时间渡河船的位移为
沿河岸方向位移为
联立解得
(2)船过河位移最小时,船头与河岸间的夹角为 ,则有
代入数据解得
解得
,指向上游
17.(1)135 m;(2) m/s
【详解】
(1)如下图所示,物体在前5 s内由坐标原点起沿x轴正方向(正东方向)做初速度为零的匀加速直线运动,其加速度为
5 s末物体沿x轴方向的位移
设5 s末物体到达P点,5 s末速度
从第5 s末开始,物体参与两个分运动:一是沿x轴正方向做速度为10 m/s的匀速直线运动,经10 s其位移
二是沿y轴正方向(正北方向)做初速度为零的匀加速直线运动,其加速度为
经10 s沿y轴正方向的位移
设15 s末物体到达Q点,则
方向为东偏北θ角,满足
(2)15 s末沿y轴正方向的速度
15 s末的速度为
设与x轴正方向夹角为
所以
即方向为东偏北45°角。
一、选择题
1.船在静水中的速度与时间的关系如图甲所示,河水的流速与离某一河岸距离的关系如图乙所示。已知两岸相互平行,若要使船以最短时间渡河(河宽为400m),则( )
A.船渡河的最短时间为80s
B.船在河水中的最大速度是5m/s
C.船渡河的位移为500m
D.船在行驶过程中船头必须与河岸垂直
2.关于不共线的两个直线运动的合运动的描述正确的是( )
A.两个匀速直线运动的合运动可能是曲线运动
B.一个匀速直线运动和一个匀加速直线运动的合运动一定是匀变速曲线运动
C.两个匀加速直线的合运动一定是匀加速直线运动
D.两个匀加速直线运动的合运动可能是直线运动也可能是曲线运动
3.甲、乙两船在同一河流中同时开始渡河,河水流速为,船在静水中的速率均为,甲、乙两船船头均与河岸成角,如图,已知甲船恰能垂直到达河正对岸的A点,乙船到达河对岸的点,之间的距离为,则正确的( )
A.若仅是河水流速增大,则两船的渡河时间都不变
B.乙船先到达对岸
C.不论河水流速如何改变,只要适当改变角,甲船总能到达正对岸的点
D.若仅是河水流速增大,则两船到达对岸时,两船之间的距离仍然为
4.如图所示,固定的光滑杆AOB,AO部分是水平的,BO部分是竖直的,用轻绳连接的环a、b分别套在AO、BO上,现同时由静止释放环a、b,当某瞬间轻绳与水平杆AO的夹角为α时,试判断此时a、b的速度之比为 ( )
A.tanα B. C.sinαcosα D.sin2α
5.湘江某段河宽300m,一小船在静水中速度为5m/s,水流速度是3m/s,则小船渡过这段湘江的最短时间( )
A.100s B.60 s C.75s D.53 s
6.如图所示,一条绳绕过光滑的定滑轮连接物体A、B,A悬挂起来,B穿在一根光滑的竖直杆上。释放A、B后,当轻绳与竖直方向夹角为θ时,B向上运动的速度达到最大值v,已知B的质量为m,重力加速度为g,则此时( )
A.A的速率为 B.轻绳的张力为mgcosθ
C.轻绳的张力为 D.轻绳张力的功率为mgv
7.人用绳子通过定滑轮拉物体A, A穿在光滑的竖直杆上,当人竖直向下拉绳使物体A匀速上升,在A匀速上升的过程中,人拉绳的速度将( ).
A.增大 B.减小 C.不变 D.不能确定
8.如图所示,汽车以速度v0向左匀速行驶,则物体M所受重力( )
A.等于绳的拉力
B.大于绳的拉力
C.小于绳的拉力
D.条件不足,无法判定
9.2021年10月29日,华南师大附中校运会开幕式隆重举行,各班进行入场式表演时,无人机从地面开始起飞,在空中进行跟踪拍摄。若无人机在水平和竖直方向运动的速度随时间变化关系图像如图所示,则无人机( )
A.在的时间内,运动轨迹为曲线 B.在的时间内,运动轨迹为直线
C.在的时间内,速度均匀变化 D.在时刻的加速度方向竖直向上
10.如图所示,有一条宽为的河道,一小船从岸边的某点渡河,渡河过程中保持船头指向与河岸始终垂直。已知小船在静水中的速度大小为,水流速度大小为。下列说法正确的是( )
A.小船渡河过程中的位移大小为
B.小船渡河的时间是
C.小船在河水中航行的轨迹是曲线
D.小船在河水中的速度是
11.质量为2 kg的质点在直角坐标系xOy平面内做曲线运动,在x轴方向的速度—时间图像和y轴方向的位移—时间图像分别如图甲、乙所示,下列说法正确的是( )
A.质点的初速度大小为4 m/s
B.质点所受的合外力大小为4 N
C.质点初速度的方向与合外力方向垂直
D.2 s末质点速度大小为8 m/s
12.一小船渡河,河宽d=180m,水流的速度v1=5m/s,小船在静水中的速度v2=4m/s,下列说法正确的是( )
A.小船能垂直河岸渡过此河,位移大小为180m
B.小船渡河过程中保持船头方向不变,若水流速度变大,则渡河时间将变短
C.调整好船头方向且保持不变,小船渡河所用的时间可能为40s
D.调整好船头方向且保持不变,小船渡河的最小位移为225m
13.一个物体同时参与不在同一直线上的一个初速度为零的匀加速直线运动和一个匀速直线运动,它的合运动的轨迹是( )
A.直线 B.双曲线 C.抛物线 D.其他曲线
14.如图所示,粗糙的水平传送带的运行速度大小为v,一物块以从传送带的边缘垂直传送带运行方向滑上传送带。在物块达到与传送带共速前的过程中,下列说法正确的是( )
A.物块的速度一直增大 B.物块的速度一直减小
C.物块可能做直线运动 D.物块一定做曲线运动
15.在河面上方20m的岸上有人用长绳栓住一条小船,开始时绳与水面的夹角为30°。人以恒定的速率v=3m/s拉绳,使小船靠岸,那么( )
A.5s时绳与水面的夹角为60°
B.5s内小船前进了15m
C.5s时小船的速率为3.75m/s
D.5s时小船距离岸边15m
二、解答题
16.一艘小船在宽的河中横渡到对岸,已知水流速度,小船在静水中的速度,,,求:
(1)船渡河最短的时间,最短时间渡河船的位移;
(2)船过河位移最小时,船头与河岸间的夹角。
17.光滑水平面上,一个质量为2kg的物体从静止开始运动,在前5s受到一个沿正东方向、大小为4N的水平恒力作用;从第5s末开始改为受到正北方向、大小为2N的水平恒力作用了10s,求:
(1)物体在15s内的位移;
(2)物体在15s末的速度。
参考答案
1.BD
【详解】
AD.在行驶过程中船头与河岸垂直,指向正对岸时,渡河时间最短,且最短时间为
A错误,D正确;
B.船运动到河中央时,速度最大,且最大速度为
B正确;
C.从岸边运动到河中间的过程中,河水的流速与到岸边的距离成正比,而垂直河岸方向上,船匀速运动,即船到岸边的距离与时间成正比,可分析得出:船顺水漂流的速度与时间成正比,因此在前半程,沿河岸平均速度
同理后半程沿河岸的平均速度也相同,因此沿河运动的位移
可得船的总位移
C错误。
故选BD。
2.BD
【详解】
A.两个匀速直线运动的合运动是匀速直线运动,故A错误;
B.一个匀速直线运动和一个匀加速直线运动的合运动,由于不共线,则合外力大小不变,与速度方向不共线,则一定是匀变速曲线运动,故B正确;
CD.两个匀加速直线的合运动,由于不共线,则合外力大小不变,但合外力与速度方向关系未知,不一定是匀加速直线运动,可能是直线运动也可能是曲线运动,故C错误,D正确。
故选BD。
3.AD
【详解】
AB.将小船的运动分解为平行于河岸和垂直于河岸两个方向,抓住分运动和合运动具有等时性,知甲乙两船到达对岸的时间相等。渡河的时间
与河水流速v0无关。则增大v0,两船的渡河时间都不变,故B错误,A正确;
C.只有甲船速度大于水流速度时,不论水流速v0如何改变,只要适当改变θ角,甲船都可能到达河的正对岸A点,故C错误;
D.若仅是河水流速v0增大,则两船到达对岸时间不变,根据速度的分解,船在水平方向的分速度仍不变,则两船之间的距离
两船之间的距离和河水流速v0无关,大小不变,故D正确。
故选AD。
4.A
【详解】
根据速度的分解可知
则a、b的速度之比为
故选A。
5.B
【详解】
渡河的最短时间只与河宽和船速有关,当船头垂直渡河时时间最短,最短时间为
故选B。
6.D
【详解】
A.物体A、B沿绳方向的速度相等,则有
故A错误;
BC.B向上运动的速度达到最大值时,对于B,绳拉力的竖直分力与重力平衡,则有
解得
故BC错误;
D.轻绳张力的功率为B克服重力做功的功率,即为
故D正确。
故选D。
7.B
【详解】
由速度的分解可知
在A匀速上升的过程中,θ角变大,则人拉绳的速度将减小。
故选B。
8.C
【详解】
汽车参与两个分运动,即沿绳子拉伸方向和垂直绳子方向(绕滑轮转动)的两个分运动,如图所示
将汽车合速度v0正交分解,可知物体上升速度等于汽车沿绳子拉伸方向的分速度,即
汽车向左匀速运动,v0不变,θ越来越小,则越来越大,所以物体上升的速度v越来越大,即物体向上做加速运动,根据牛顿第二定律可知,轻绳的拉力大于物体受的重力。
故选C。
9.C
【详解】
A.在的时间内,无人机沿x方向和y方向均做初速度为零的匀加速度直线运动,其合运动仍是直线运动,故A错误;
B.在的时间内,无人机的加速度沿y轴负向,但初速度为时刻的末速度,方向不是沿y轴方向,初速度和加速度不共线,因此运动轨迹应是曲线,故B错误;
C.在的时间内,无人机加速度沿y轴负向,且为定值,因此其速度均匀变化,故C正确;
D.在时刻,无人机有x轴负方向和y轴正方向的加速度分量,合加速度方向不是竖直向上,故D错误。
故选C。
10.B
【详解】
A.小船参与了两个方向的运动,一个是垂直于河岸的运动,一个是沿着河岸的运动,小船到达河对岸时,垂直于河岸的位移为,总位移大于,A错误;
B.由于渡河过程中保持船头指向与河岸始终垂直,故
解得
选项B正确;
C.小船垂直于河岸方向做匀速直线运动,沿河岸方向也做匀速直线运动,所以小船的实际运动为匀速直线运动,C错误;
D.小船在河水中的速度为
D错误。
故选B。
11.B
【详解】
AD.x方向的初速度为4m/s,y方向做匀速直线运动,其速度为4m/s,质点的初速度
为
2s末速度为
AD错误;
B.y方向的加速度为0,x方向的加速度为
由牛顿第二定律可得
B正确;
C.由于只有x方向有加速度,所以合外力与x方向同向,而初速度与x方向不垂直,所以质点初速度的方向与合外力方向不垂直,C错误。
故选B。
12.D
【详解】
A.由于小船在静水中的速度v2=4m/s小于水流速度v1=5m/s,小船不能垂直河岸渡过此河,故A错误;
B.若保持船头方向不变,水流速度变大,垂直河岸方向的分运动速度不变,则渡河时间不变,故B错误;
CD.当小船在静水中的速度与河岸垂直,渡河时间最短,则最短时间为
故小船渡河所用的时间不可能为40s,故C错误;
D.由于小船在静水中的速度v2=4m/s小于水流速度v1=5m/s,则当合速度垂直于船速时,航程最短,有
故D正确。
故选D。
13.C
【详解】
不在同一直线上的匀加速直线运动和匀速直线运动合成时,只有一个方向有加速度,合加速度的方向就在该方向上,与合速度的方向不在同一直线上,因此合运动是曲线运动,即为抛物线。
故选C。
14.D
【详解】
AB.物块在沿着传送带的方向做匀加速直线运动,即由0加到v,在垂直传动带速度方向做匀减速直线运动,即由v0减到0,所以速度的大小由v0变到v,若,则物块速度先减小后增大,若,则速度一直减小,故AB错误;
CD.由上分析可知,物块受到的摩擦力有两个效果,一个是垂直传送带方向让物块减速,加一个是沿传送带方向让物块加速,故最终的摩擦力方向与初速度的方向存在夹角,不在同一直线上,故物块一定做曲线运动,故D正确,C错误。
故选D。
15.D
【详解】
开始时滑轮与船之间的绳长为
船头到河岸的距离为
5s时滑轮与船之间的绳长为
船头到河岸的距离为
5s内小船前进了
此时绳与水面的夹角θ的余弦值为
即θ不等于60°。
5s时小船的速率为
综上所述可知ABC错误,D正确。
故选D。
16.(1),;(2),指向上游
【详解】
(1)船渡河时,保持船头方向与河岸垂直时,渡河时间最短,有
最短时间渡河船的位移为
沿河岸方向位移为
联立解得
(2)船过河位移最小时,船头与河岸间的夹角为 ,则有
代入数据解得
解得
,指向上游
17.(1)135 m;(2) m/s
【详解】
(1)如下图所示,物体在前5 s内由坐标原点起沿x轴正方向(正东方向)做初速度为零的匀加速直线运动,其加速度为
5 s末物体沿x轴方向的位移
设5 s末物体到达P点,5 s末速度
从第5 s末开始,物体参与两个分运动:一是沿x轴正方向做速度为10 m/s的匀速直线运动,经10 s其位移
二是沿y轴正方向(正北方向)做初速度为零的匀加速直线运动,其加速度为
经10 s沿y轴正方向的位移
设15 s末物体到达Q点,则
方向为东偏北θ角,满足
(2)15 s末沿y轴正方向的速度
15 s末的速度为
设与x轴正方向夹角为
所以
即方向为东偏北45°角。
