2021—2022学年人教版七年级数学下册5.1.1相交线课后练习(Word版含简答)
文档属性
| 名称 | 2021—2022学年人教版七年级数学下册5.1.1相交线课后练习(Word版含简答) |  | |
| 格式 | docx | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-18 23:48:54 | ||
图片预览


文档简介
5.1.1《相交线》课时练习
一、选择题
1.三条共点直线都与第四条直线相交,一共有( )对对顶角.
A.8 B.24 C.7 D.12
2.如图,点O在直线AB上,若∠1=40°,则∠2的度数是( )
A.50° B.60° C.140° D.150°
3.如图,直线与相交于点,,若,则的度数为( ).
A. B. C. D.
4.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠COE=140°,则∠BOC=( )
A.50° B.60° C.70° D.80°
5.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠COE=140°,则∠BOC=( )
A.50° B.60° C.70° D.80°
6.如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=34°,则∠BOD大小为( )
A.22° B.34° C.56° D.90°
7.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
8.下列说法正确的是( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两角之和为180°,则这两个角互为邻补角
D.—个角的邻补角可能是锐角、钝角或直角
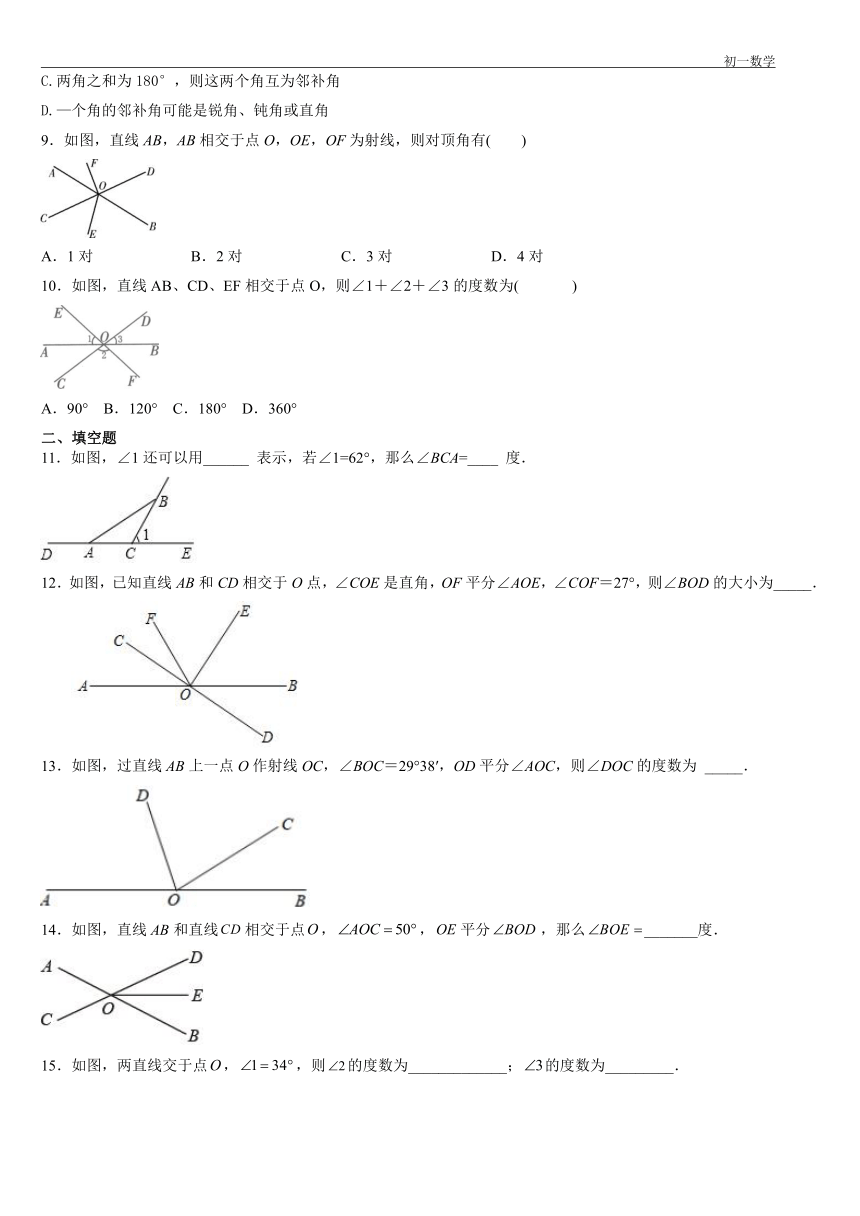
9.如图,直线AB,AB相交于点O,OE,OF为射线,则对顶角有( )
A.1对 B.2对 C.3对 D.4对
10.如图,直线AB、CD、EF相交于点O,则∠1+∠2+∠3的度数为( )
A.90° B.120° C.180° D.360°
二、填空题
11.如图,∠1还可以用______ 表示,若∠1=62°,那么∠BCA=____ 度.
12.如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=27°,则∠BOD的大小为_____.
13.如图,过直线AB上一点O作射线OC,∠BOC=29°38′,OD平分∠AOC,则∠DOC的度数为 _____.
14.如图,直线和直线相交于点,,平分,那么_______度.
15.如图,两直线交于点,,则的度数为_____________;的度数为_________.
三、解答题
16.直线、相交于点,平分,,,求与的度数.
17.如图,直线AB与直线CD相交于点O,射线OE在内部,OA平分.
(1)当时,写出图中所有与互补的角.
(2)当时,求的度数.
18.如图1,直线AB上任取一点O,过点O作射线OC(点C在直线AB上方),且∠BOC=2∠AOC,以O为顶点作∠MON=90°,点M在射线OB上,点N在直线AB下方,点D是射线ON反向延长线上的一点.
(1)求∠COD的度数;
(2)如图2,将∠MON绕点O逆时针旋转α度(0°<α<180°),若三条射线OD、OC、OA,当其中一条射线与另外两条射线所夹角的度数之比为1:2时,求∠BON的度数.
19.如图,直线、相交于点,平分,平分,.
(1)求的度数;
(2)求的度数.
20.如图,直线,相交于点,平分.
(1)若,求的度数;
(2)若,求的度数.
21.如图,已知直线,相交于点,与互余.
(1)若,求的度数;
(2)若,求的度数.
22.如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶5
(1)如图,若∠BOD=70°,求∠BOE
(2)如图,若OF平分∠BOE,∠BOF=∠AOC+10°,求∠EOF
23.已知点O为直线AB上一点,将直角三角板MON按如图所示放置,且直角顶点在O处,在内部作射线OC,且OC恰好平分.
(1)若,求的度数;
(2)若,求的度数
【参考答案】
1.D 2.C 3.C 4.D5.D 6.A 7.C 8.D 9.B 10.C
11.
12.36°
13.
14.25
15.
16.;
17.(1)、、;(2)36°.
18.(1)∠COD=30°;(2)40°或20°或30°
19.(1)30°,(2)45°.
20.(1);(2)
21.(1)58°;(2)120°
22.(1) 160°;(2) 80°
初一数学
23.(1)48°;(2)45°
一、选择题
1.三条共点直线都与第四条直线相交,一共有( )对对顶角.
A.8 B.24 C.7 D.12
2.如图,点O在直线AB上,若∠1=40°,则∠2的度数是( )
A.50° B.60° C.140° D.150°
3.如图,直线与相交于点,,若,则的度数为( ).
A. B. C. D.
4.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠COE=140°,则∠BOC=( )
A.50° B.60° C.70° D.80°
5.如图,直线AB、CD相交于点O,OE平分∠AOD,若∠COE=140°,则∠BOC=( )
A.50° B.60° C.70° D.80°
6.如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=34°,则∠BOD大小为( )
A.22° B.34° C.56° D.90°
7.如图,三条直线l1,l2,l3相交于一点,则∠1+∠2+∠3等于( )
A.90° B.120° C.180° D.360°
8.下列说法正确的是( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两角之和为180°,则这两个角互为邻补角
D.—个角的邻补角可能是锐角、钝角或直角
9.如图,直线AB,AB相交于点O,OE,OF为射线,则对顶角有( )
A.1对 B.2对 C.3对 D.4对
10.如图,直线AB、CD、EF相交于点O,则∠1+∠2+∠3的度数为( )
A.90° B.120° C.180° D.360°
二、填空题
11.如图,∠1还可以用______ 表示,若∠1=62°,那么∠BCA=____ 度.
12.如图,已知直线AB和CD相交于O点,∠COE是直角,OF平分∠AOE,∠COF=27°,则∠BOD的大小为_____.
13.如图,过直线AB上一点O作射线OC,∠BOC=29°38′,OD平分∠AOC,则∠DOC的度数为 _____.
14.如图,直线和直线相交于点,,平分,那么_______度.
15.如图,两直线交于点,,则的度数为_____________;的度数为_________.
三、解答题
16.直线、相交于点,平分,,,求与的度数.
17.如图,直线AB与直线CD相交于点O,射线OE在内部,OA平分.
(1)当时,写出图中所有与互补的角.
(2)当时,求的度数.
18.如图1,直线AB上任取一点O,过点O作射线OC(点C在直线AB上方),且∠BOC=2∠AOC,以O为顶点作∠MON=90°,点M在射线OB上,点N在直线AB下方,点D是射线ON反向延长线上的一点.
(1)求∠COD的度数;
(2)如图2,将∠MON绕点O逆时针旋转α度(0°<α<180°),若三条射线OD、OC、OA,当其中一条射线与另外两条射线所夹角的度数之比为1:2时,求∠BON的度数.
19.如图,直线、相交于点,平分,平分,.
(1)求的度数;
(2)求的度数.
20.如图,直线,相交于点,平分.
(1)若,求的度数;
(2)若,求的度数.
21.如图,已知直线,相交于点,与互余.
(1)若,求的度数;
(2)若,求的度数.
22.如图,直线AB和CD相交于点O,OE把∠AOC分成两部分,且∠AOE∶∠EOC=2∶5
(1)如图,若∠BOD=70°,求∠BOE
(2)如图,若OF平分∠BOE,∠BOF=∠AOC+10°,求∠EOF
23.已知点O为直线AB上一点,将直角三角板MON按如图所示放置,且直角顶点在O处,在内部作射线OC,且OC恰好平分.
(1)若,求的度数;
(2)若,求的度数
【参考答案】
1.D 2.C 3.C 4.D5.D 6.A 7.C 8.D 9.B 10.C
11.
12.36°
13.
14.25
15.
16.;
17.(1)、、;(2)36°.
18.(1)∠COD=30°;(2)40°或20°或30°
19.(1)30°,(2)45°.
20.(1);(2)
21.(1)58°;(2)120°
22.(1) 160°;(2) 80°
初一数学
23.(1)48°;(2)45°
