人教版五年级下册数学寒假提升真题卷(含答案)
文档属性
| 名称 | 人教版五年级下册数学寒假提升真题卷(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 117.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 10:49:17 | ||
图片预览



文档简介
人教版五年级下册数学寒假提升真题卷
一.选择题(共6题,共12分)
1.两个奇数的和是( )。
A.质数 B.合数 C.偶数
2.7□2是3的倍数,□里最大能填( )。
A.5 B.6 C.7 D.9
3.自然数中,凡是17的倍数( )。
A.都是偶数 B.有偶数有奇数 C.都是奇数
4.有13个乒乓球,其中12个的质量相同,另一个轻一点,如果用天平称,至少称( )次保证能找到这个较轻的乒乓球。
A.2 B.3 C.4 D.6
5.从12时到12时30分,分针绕中心点( )。
A.逆时针旋转了90° B.顺时针旋转了90° C.顺时针旋转了180°
6.下列数中,( )既是2的倍数,又是5的倍数。
A.12 B.15 C.20 D.37
二.判断题(共6题,共11分)
1.一个长方体,它的长、宽、高都扩大2倍,它的体积扩大6倍。( )
2.个位上是0的自然数一定是2和5的倍数。( )
3.一个三位数各位上的数字都相同,这个数一定是3的倍数。( )
4.所有的偶数都是合数,所有的奇数都是质数。( )
5.站在不同的位置观察长方体,每次最多能看到六个面。( )
6.一个数的倍数一定大于这个数的因数。( )
三.填空题(共6题,共23分)
1.三个连续的偶数,最小的是n,另外两个数分别是( )和( )。
2.在括号内填上合适的质数。
①16=( )+( ) ②35=( )×( )
③22=( )×( ) ④30=( )+( )
⑤32=( )+( ) ⑥65=( )×( )
3.一个30°的角,将它的一条边旋转( )°可得到一个直角。
4.在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为( ),这个定点称为( ),转动的角为( )。
5.下边的图形要拼成一个大正方体,至少还需要( )个。
6.填一填。
3.5m2=( )dm2 6.5L=( )mL
34000mL=( )cm3 =( )dm3
四.计算题(共1题,共4分)
1.算一算。
五.作图题(共3题,共17分)
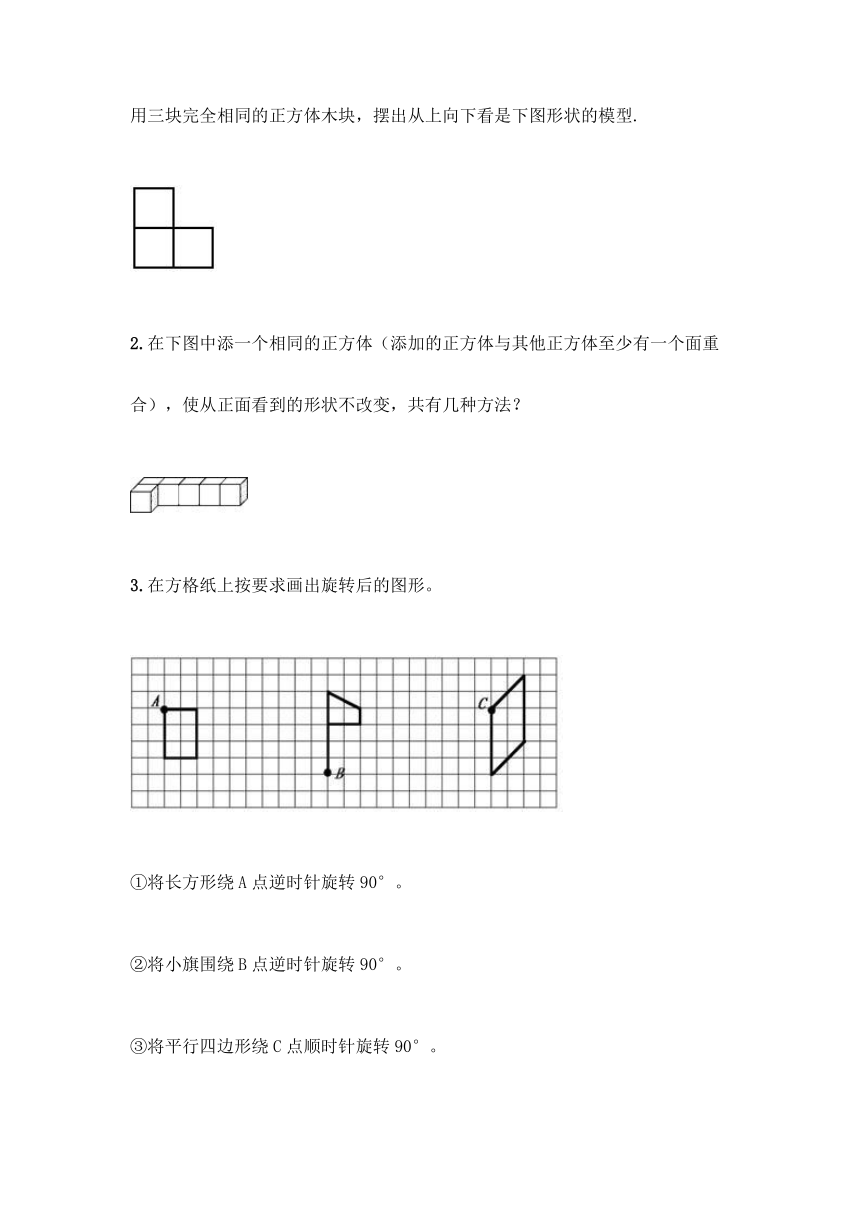
1.摆一摆.
用三块完全相同的正方体木块,摆出从上向下看是下图形状的模型.
2.在下图中添一个相同的正方体(添加的正方体与其他正方体至少有一个面重合),使从正面看到的形状不改变,共有几种方法?
3.在方格纸上按要求画出旋转后的图形。
①将长方形绕A点逆时针旋转90°。
②将小旗围绕B点逆时针旋转90°。
③将平行四边形绕C点顺时针旋转90°。
六.解答题(共6题,共31分)
1.教室里有一盏灯亮着,突然停电了,李老师拉了一下电灯的开关,如果这个班有36名同学,每人都拉一下开关,最后灯是亮着还是关着?请说出你的理由.
2.如下图,将三角形BAC顺时针旋转30°得到三角形B'A'C,若AC垂直于A'B',则∠A和∠BCB'的度数各是多少度?
3.有29瓶同样的纯净水,向其中一瓶中加入一些盐,如果用天平称,至少称几次能保证找出加盐的纯净水
4.有21个小铁球,其中一个是空心的,你如何利用天平找到它。
5.有3袋糖果,其中两袋每袋1千克,另一袋不是1千克,但不知道比1千克重还是轻,你能用天平找出来吗?写出简要过程。
6.今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币和真币的重量不同.现需弄清楚伪币究竟比真币轻还是重、但只有一架没有砝码的天平,那么怎样利用这架天平称两次,来达到目的?
参考答案
一.选择题
1.C
2.D
3.B
4.B
5.C
6.C
二.判断题
1.×
2.√
3.√
4.×
5.×
6.×
三.填空题
1.n+2;n+4
2.①5+11(或3+13);②5×7;③2×11;④13+17(或11+19,7+23);⑤13+19(或3+29);⑥13×5
3.60
4.旋转;旋转中心;旋转角
5.7
6.350;6500;34000;34
四.计算题
1.;0;
五.作图题
1.
2.解:共有10种方法.
3.
六.解答题
1.解:李老师拉了一下后,此时开关的状态为关闭.
此后第一位同学拉后:开;
第二位:关;
第三位:开;
第四位:关;
…,
由此可以发现,奇数个同学拉后,开关状态总为开启,偶数个同学拉后,开关状态总为关闭.
36为偶数,所以最后灯是关着的.
答:最后灯是关着的.
2.解:∠A=∠A'=90°-30°=60°,因为三角形B'A'C是三角形BAC旋转30°得到,所以∠BCB'=30°。
答:∠A是60°,∠BCB'是30°。
3.解:把29瓶分成10瓶、10瓶、9瓶;
第一次:两端各放10瓶,如果平衡次品就在9瓶中;如果不平衡,次品在下沉的那10瓶中;
第二次:①把9瓶平均分成3份,每份3瓶;称1次找出次品所在的3瓶,再称1次找出次品;共称3次;
②把次品所在的10瓶分成3、3、4,称1次找出次品所在的4瓶;再称1次找出次品所在的2瓶,再称1次找出次品,共称4次.
答:至少称4次能保证找出加盐的纯净水.
4.解:第一次,分成三组即7、7、7,将其中两组分别放在天平的两端,若天平平衡则空心球在没被选的一组中,若天平不平衡则轻的一端含有空心球;
第二次,分成三组即2、2、3,将其中相等两组分别放在天平的两端,若天平平衡则空心球在没被选的一组中,若天平不平衡则轻的一端含有空心球;
第三次,①若空心球在3个中,则任取2个球放在天平的两端,若天平平衡则空心球是没被选的个一个,若天平不平衡则轻的一端是空心球;②若空心球在2个中,则轻的一端是空心球。
5.能用天平找出来。将三袋糖果编号为甲、乙、丙;将甲、乙放在天平的两端,若天平平衡,则说明丙袋不是1千克;若天平不平衡,把较重的那一袋取下,并把丙袋放上去,若天平平衡,则说明刚才取下的那一袋不是1千克,若天平不平衡,则刚才未取下的那一袋不是1千克.
6.解:101枚硬币,如果进行称重的话应该保证天平两边的硬币数相等.因此应该首先拿掉一个,把剩下的100枚硬币在天平两边各放50个.如果这时天平两边重量相等的话,就说明剩下的那个是伪币.只要任意拿出一个真币和这个伪币再称一次就可以知道真币和伪币那种比较重了.
如果天平两边重量不相等的话,就是说伪币还在这100个硬币中.可以拿出其中比较轻的50个.这时同样还是把他们分成两个25枚,分到天平两边称重.
如果两边重量相等,说明这50个硬币都是真的.伪币在比较重的那50个中,因此伪币就应该比真币重.如果两边重量不相等,说明伪币就在这50个比较轻的硬币中,显然伪币就应该比真币轻.
同样道理,也可以把比较重的那50个硬币分成两个25进行称重,同样也可以得出结论
一.选择题(共6题,共12分)
1.两个奇数的和是( )。
A.质数 B.合数 C.偶数
2.7□2是3的倍数,□里最大能填( )。
A.5 B.6 C.7 D.9
3.自然数中,凡是17的倍数( )。
A.都是偶数 B.有偶数有奇数 C.都是奇数
4.有13个乒乓球,其中12个的质量相同,另一个轻一点,如果用天平称,至少称( )次保证能找到这个较轻的乒乓球。
A.2 B.3 C.4 D.6
5.从12时到12时30分,分针绕中心点( )。
A.逆时针旋转了90° B.顺时针旋转了90° C.顺时针旋转了180°
6.下列数中,( )既是2的倍数,又是5的倍数。
A.12 B.15 C.20 D.37
二.判断题(共6题,共11分)
1.一个长方体,它的长、宽、高都扩大2倍,它的体积扩大6倍。( )
2.个位上是0的自然数一定是2和5的倍数。( )
3.一个三位数各位上的数字都相同,这个数一定是3的倍数。( )
4.所有的偶数都是合数,所有的奇数都是质数。( )
5.站在不同的位置观察长方体,每次最多能看到六个面。( )
6.一个数的倍数一定大于这个数的因数。( )
三.填空题(共6题,共23分)
1.三个连续的偶数,最小的是n,另外两个数分别是( )和( )。
2.在括号内填上合适的质数。
①16=( )+( ) ②35=( )×( )
③22=( )×( ) ④30=( )+( )
⑤32=( )+( ) ⑥65=( )×( )
3.一个30°的角,将它的一条边旋转( )°可得到一个直角。
4.在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为( ),这个定点称为( ),转动的角为( )。
5.下边的图形要拼成一个大正方体,至少还需要( )个。
6.填一填。
3.5m2=( )dm2 6.5L=( )mL
34000mL=( )cm3 =( )dm3
四.计算题(共1题,共4分)
1.算一算。
五.作图题(共3题,共17分)
1.摆一摆.
用三块完全相同的正方体木块,摆出从上向下看是下图形状的模型.
2.在下图中添一个相同的正方体(添加的正方体与其他正方体至少有一个面重合),使从正面看到的形状不改变,共有几种方法?
3.在方格纸上按要求画出旋转后的图形。
①将长方形绕A点逆时针旋转90°。
②将小旗围绕B点逆时针旋转90°。
③将平行四边形绕C点顺时针旋转90°。
六.解答题(共6题,共31分)
1.教室里有一盏灯亮着,突然停电了,李老师拉了一下电灯的开关,如果这个班有36名同学,每人都拉一下开关,最后灯是亮着还是关着?请说出你的理由.
2.如下图,将三角形BAC顺时针旋转30°得到三角形B'A'C,若AC垂直于A'B',则∠A和∠BCB'的度数各是多少度?
3.有29瓶同样的纯净水,向其中一瓶中加入一些盐,如果用天平称,至少称几次能保证找出加盐的纯净水
4.有21个小铁球,其中一个是空心的,你如何利用天平找到它。
5.有3袋糖果,其中两袋每袋1千克,另一袋不是1千克,但不知道比1千克重还是轻,你能用天平找出来吗?写出简要过程。
6.今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币和真币的重量不同.现需弄清楚伪币究竟比真币轻还是重、但只有一架没有砝码的天平,那么怎样利用这架天平称两次,来达到目的?
参考答案
一.选择题
1.C
2.D
3.B
4.B
5.C
6.C
二.判断题
1.×
2.√
3.√
4.×
5.×
6.×
三.填空题
1.n+2;n+4
2.①5+11(或3+13);②5×7;③2×11;④13+17(或11+19,7+23);⑤13+19(或3+29);⑥13×5
3.60
4.旋转;旋转中心;旋转角
5.7
6.350;6500;34000;34
四.计算题
1.;0;
五.作图题
1.
2.解:共有10种方法.
3.
六.解答题
1.解:李老师拉了一下后,此时开关的状态为关闭.
此后第一位同学拉后:开;
第二位:关;
第三位:开;
第四位:关;
…,
由此可以发现,奇数个同学拉后,开关状态总为开启,偶数个同学拉后,开关状态总为关闭.
36为偶数,所以最后灯是关着的.
答:最后灯是关着的.
2.解:∠A=∠A'=90°-30°=60°,因为三角形B'A'C是三角形BAC旋转30°得到,所以∠BCB'=30°。
答:∠A是60°,∠BCB'是30°。
3.解:把29瓶分成10瓶、10瓶、9瓶;
第一次:两端各放10瓶,如果平衡次品就在9瓶中;如果不平衡,次品在下沉的那10瓶中;
第二次:①把9瓶平均分成3份,每份3瓶;称1次找出次品所在的3瓶,再称1次找出次品;共称3次;
②把次品所在的10瓶分成3、3、4,称1次找出次品所在的4瓶;再称1次找出次品所在的2瓶,再称1次找出次品,共称4次.
答:至少称4次能保证找出加盐的纯净水.
4.解:第一次,分成三组即7、7、7,将其中两组分别放在天平的两端,若天平平衡则空心球在没被选的一组中,若天平不平衡则轻的一端含有空心球;
第二次,分成三组即2、2、3,将其中相等两组分别放在天平的两端,若天平平衡则空心球在没被选的一组中,若天平不平衡则轻的一端含有空心球;
第三次,①若空心球在3个中,则任取2个球放在天平的两端,若天平平衡则空心球是没被选的个一个,若天平不平衡则轻的一端是空心球;②若空心球在2个中,则轻的一端是空心球。
5.能用天平找出来。将三袋糖果编号为甲、乙、丙;将甲、乙放在天平的两端,若天平平衡,则说明丙袋不是1千克;若天平不平衡,把较重的那一袋取下,并把丙袋放上去,若天平平衡,则说明刚才取下的那一袋不是1千克,若天平不平衡,则刚才未取下的那一袋不是1千克.
6.解:101枚硬币,如果进行称重的话应该保证天平两边的硬币数相等.因此应该首先拿掉一个,把剩下的100枚硬币在天平两边各放50个.如果这时天平两边重量相等的话,就说明剩下的那个是伪币.只要任意拿出一个真币和这个伪币再称一次就可以知道真币和伪币那种比较重了.
如果天平两边重量不相等的话,就是说伪币还在这100个硬币中.可以拿出其中比较轻的50个.这时同样还是把他们分成两个25枚,分到天平两边称重.
如果两边重量相等,说明这50个硬币都是真的.伪币在比较重的那50个中,因此伪币就应该比真币重.如果两边重量不相等,说明伪币就在这50个比较轻的硬币中,显然伪币就应该比真币轻.
同样道理,也可以把比较重的那50个硬币分成两个25进行称重,同样也可以得出结论
同课章节目录
