2021-2022学年人教版七年级数学下册5.1.2垂线课后练习(Word版含简答)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.1.2垂线课后练习(Word版含简答) |

|
|
| 格式 | docx | ||
| 文件大小 | 174.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览

文档简介
2021——2022学年度人教版七年级数学下册 第五章 相交线与平行线 5.1.2 垂线课后练习
一、选择题
1.为直线上一点,,若,则( )
A.30° B.40° C.50° D.60°
2.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为( )
A.35° B.45° C.55° D.25°
3.如图,直线AB,CD相交于点O,EO⊥AB,若∠AOC=24°,则∠DOE的度数是( )
A.24° B.54° C.66° D.76°
4.如图,AC⊥BC,AC=4.5,若点P在直线BC上,则AP的长可能是( ).
A.5 B.4 C.3 D.2
5.如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中:①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.其中正确的有( )
A.3个 B.4个 C.5个 D.6个
6.如图,学校举行运动会,为主席台位置,对面是观众席,甲、乙、丙、丁四位同学分别坐在观众席的点,,,的位置上,已知,,,四点在一条直线上,且,问距离主席台最近的同学是()
A.甲 B.乙 C.丙 D.丁
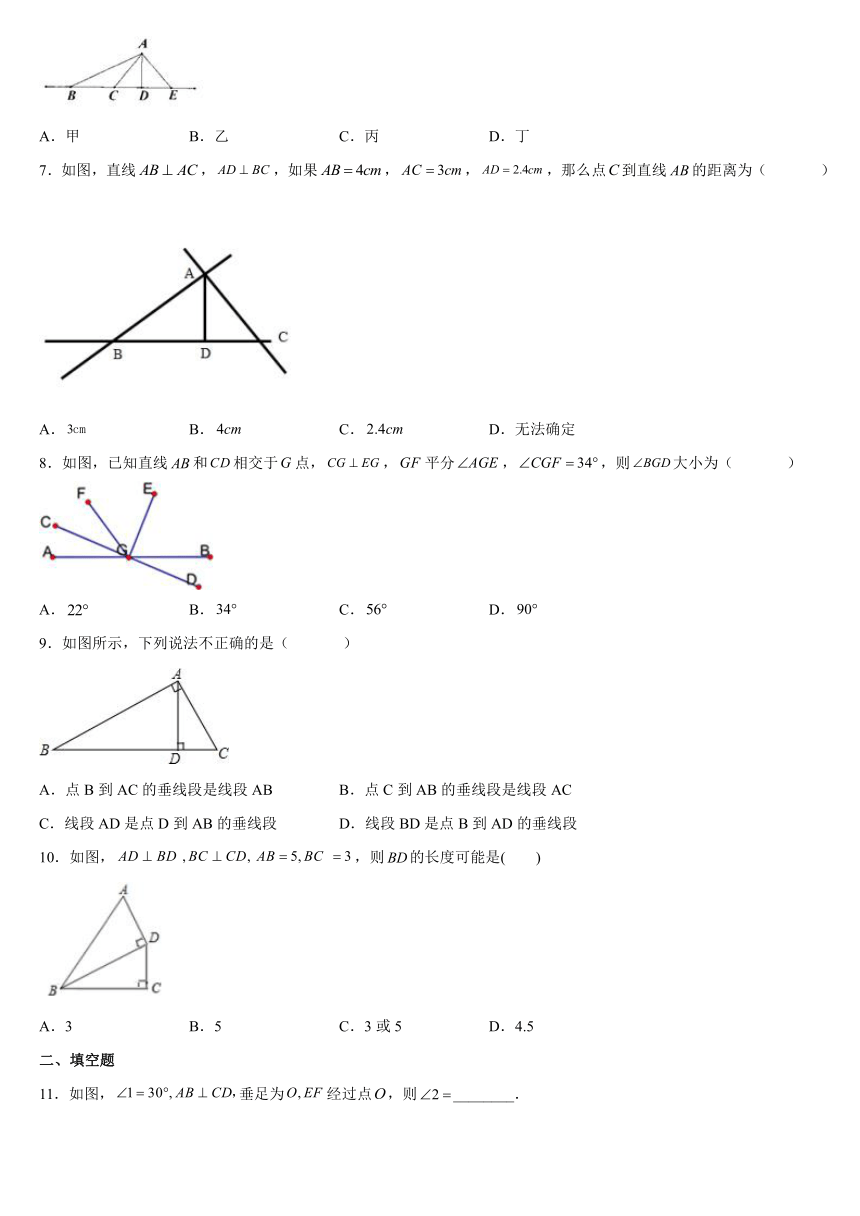
7.如图,直线,,如果,,,那么点到直线的距离为( )
A. B. C. D.无法确定
8.如图,已知直线和相交于点,,平分,,则大小为( )
A. B. C. D.
9.如图所示,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB B.点C到AB的垂线段是线段AC
C.线段AD是点D到AB的垂线段 D.线段BD是点B到AD的垂线段
10.如图,,则的长度可能是( )
A.3 B.5 C.3或5 D.4.5
二、填空题
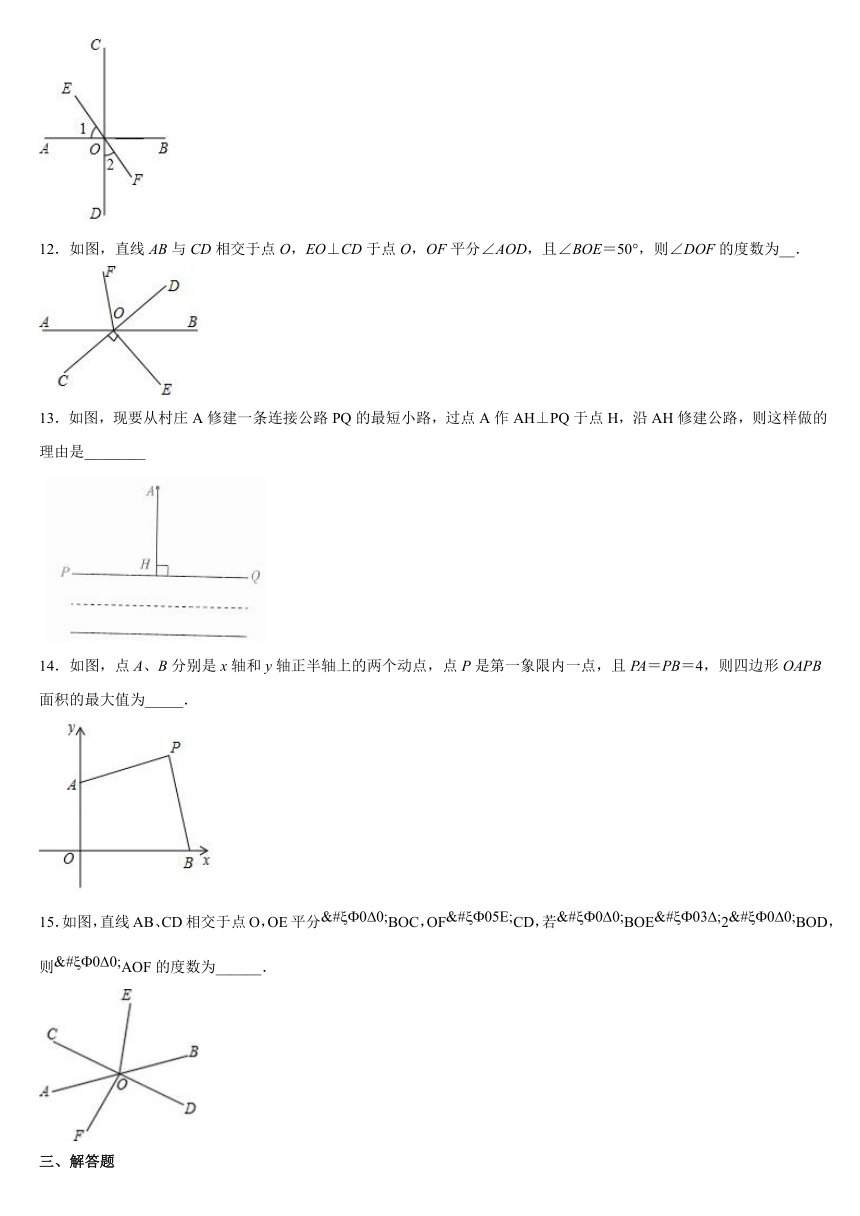
11.如图,垂足为经过点,则________.
12.如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°,则∠DOF的度数为__.
13.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是________
14.如图,点A、B分别是x轴和y轴正半轴上的两个动点,点P是第一象限内一点,且PA=PB=4,则四边形OAPB面积的最大值为_____.
15.如图,直线AB、CD相交于点O,OE平分BOC,OFCD,若BOE2BOD,则AOF的度数为______.
三、解答题
16.如图,直线AB、CD相交于点O,OC是∠AOE的平分线,OF⊥CD,∠BOD与∠EOF互余吗?为什么?
17.如图所示,直线与相交于点,于点,,求与的度数.
18.如图,已知直线相交于点O,.
(1)若,求的度数.
(2)若,求的度数.
19.已知:点是直线外一点,点、、是直线上三点,分别连接、、.
(1)通过测量的方法,比较、、的大小,直接用“”连接;
(2)在直线上能否找到一点,使的长度最短?如果有,请在图中作出线段,并说明它的理论依据;如果没有,请说明理由.
20.如图,直线,相交于点,,.
(1)若,求的度数;
(2)若,求和的度数.
21.如图,直线和直线相交于点,,垂足为,平分.
(1)若,求的度数;
(2)若,求的度数.
22.如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
23.如图,AC⊥CD,∠BED=90°.填空:
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
【参考答案】
1.C 2.A 3.C 4.A 5.A 6.C 7.A 8.A 9.C 10.D
11.60°.
12.
13.垂线段最短
14.16
15.54°
16.∠BOD与∠EOF互余.
17.
18.(1)53°;(2)150°
19.(1);(2)垂线段最短
20.(1)135°;(2)∠2 =60°,150°
21.(1);(2);
22.(1)略;(2)OF<OG;(3)∠AOD=70°,∠DOE=20°.
23.(1) 90 ;(2) 互相垂直 ;(3) BE,DC ;(4) DC, BE,连结直线外一点与直线上各点的所有线段中,垂线段最短
一、选择题
1.为直线上一点,,若,则( )
A.30° B.40° C.50° D.60°
2.如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠CON=55°,则∠AOM的度数为( )
A.35° B.45° C.55° D.25°
3.如图,直线AB,CD相交于点O,EO⊥AB,若∠AOC=24°,则∠DOE的度数是( )
A.24° B.54° C.66° D.76°
4.如图,AC⊥BC,AC=4.5,若点P在直线BC上,则AP的长可能是( ).
A.5 B.4 C.3 D.2
5.如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中:①AB⊥AC;②AD与AC互相垂直;③点C到AB的垂线段是线段AB;④点A到BC的距离是线段AD的长度;⑤线段AB的长度是点B到AC的距离;⑥线段AB是点B到AC的距离.其中正确的有( )
A.3个 B.4个 C.5个 D.6个
6.如图,学校举行运动会,为主席台位置,对面是观众席,甲、乙、丙、丁四位同学分别坐在观众席的点,,,的位置上,已知,,,四点在一条直线上,且,问距离主席台最近的同学是()
A.甲 B.乙 C.丙 D.丁
7.如图,直线,,如果,,,那么点到直线的距离为( )
A. B. C. D.无法确定
8.如图,已知直线和相交于点,,平分,,则大小为( )
A. B. C. D.
9.如图所示,下列说法不正确的是( )
A.点B到AC的垂线段是线段AB B.点C到AB的垂线段是线段AC
C.线段AD是点D到AB的垂线段 D.线段BD是点B到AD的垂线段
10.如图,,则的长度可能是( )
A.3 B.5 C.3或5 D.4.5
二、填空题
11.如图,垂足为经过点,则________.
12.如图,直线AB与CD相交于点O,EO⊥CD于点O,OF平分∠AOD,且∠BOE=50°,则∠DOF的度数为__.
13.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是________
14.如图,点A、B分别是x轴和y轴正半轴上的两个动点,点P是第一象限内一点,且PA=PB=4,则四边形OAPB面积的最大值为_____.
15.如图,直线AB、CD相交于点O,OE平分BOC,OFCD,若BOE2BOD,则AOF的度数为______.
三、解答题
16.如图,直线AB、CD相交于点O,OC是∠AOE的平分线,OF⊥CD,∠BOD与∠EOF互余吗?为什么?
17.如图所示,直线与相交于点,于点,,求与的度数.
18.如图,已知直线相交于点O,.
(1)若,求的度数.
(2)若,求的度数.
19.已知:点是直线外一点,点、、是直线上三点,分别连接、、.
(1)通过测量的方法,比较、、的大小,直接用“”连接;
(2)在直线上能否找到一点,使的长度最短?如果有,请在图中作出线段,并说明它的理论依据;如果没有,请说明理由.
20.如图,直线,相交于点,,.
(1)若,求的度数;
(2)若,求和的度数.
21.如图,直线和直线相交于点,,垂足为,平分.
(1)若,求的度数;
(2)若,求的度数.
22.如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
23.如图,AC⊥CD,∠BED=90°.填空:
(1)∠ACD=_____度;
(2)直线AD与BE的位置关系是__________;
(3)点B到直线AD的距离是线段________的长度,点D到直线AB的距离是线段______的长度;
(4)在线段DA,DB,DC中,最短的是线段______;在线段BA,BE,BD中,最短的是线段______,理由是_____________________________________.
【参考答案】
1.C 2.A 3.C 4.A 5.A 6.C 7.A 8.A 9.C 10.D
11.60°.
12.
13.垂线段最短
14.16
15.54°
16.∠BOD与∠EOF互余.
17.
18.(1)53°;(2)150°
19.(1);(2)垂线段最短
20.(1)135°;(2)∠2 =60°,150°
21.(1);(2);
22.(1)略;(2)OF<OG;(3)∠AOD=70°,∠DOE=20°.
23.(1) 90 ;(2) 互相垂直 ;(3) BE,DC ;(4) DC, BE,连结直线外一点与直线上各点的所有线段中,垂线段最短
