1.3.2函数的奇偶性(二)

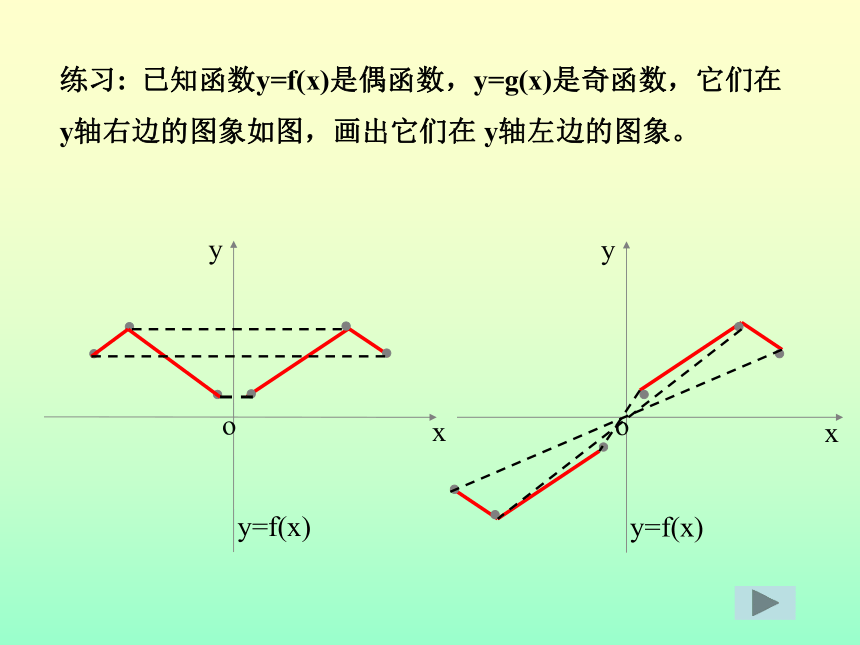
课件11张PPT。1.3.2函数的奇偶性(二)oyx练习: 已知函数y=f(x)是偶函数，y=g(x)是奇函数，它们在
y轴右边的图象如图，画出它们在 y轴左边的图象。y=f(x)oyxy=f(x)一.函数奇偶性的应用
1.已知f(x)是定义 在区间[a，a+1]上的奇函数
则 ①a = ; ②f(0) = .
结论:若f(x)是定义在R上的奇函数，则f(0)=0.2. 设函数 ，已知 是偶函数，求实数m的值.3.已知f（x）=x5+ax3+bx-8，且f（-2）=10，
且f（2）等于（ ）
A、-26 B、-18 C、-10 D、10例1 已知f(x)是偶函数，且当 时， ,求当 时f(x)的解析式.例2 (1)设f (x)是偶函数，g (x)是奇函数，
且求函数f (x)，g(x)的解析式；4. 如图⑴，给出了奇函数y＝f (x)的局部
图象，求f (－4).5. 如图⑵，给出了偶函数y＝f (x)的局部
图象，试比较f (1)与 f (3) 的大小.⑴⑵二.单调性与奇偶性综合例3．已知f(x)是奇函数，在(0，＋∞)上是增
函数，证明：f(x)在(－∞，0)上也是增函数规律：
偶函数在关于原点对称的区间上单调性相反；
奇函数在关于原点对称的区间上单调性一致． 练:奇函数在[3，5]上最大值是6，最小值是4，
则在[-5，-3]上的最大值（ ），最小值（ ）
例4.定义在（-2，2）上的奇函数f（x），满足 f(1+ a) + f(a) > 0，已知f（x）在（-2，2）是减函数，求a的取值范围。
?


变2.定义在（-2，2）上的偶函数f(x)在区间[0,2]上单调递减，若 f(1-m)?


变1.定义在（-2，2）上的奇函数f（x），满足 f(1+ a) + f(a) > 0， f（x）在
[0,2）是减函数，求a的取值范围。
?

变3. 已知f(x)是定义在R上的偶函数，且在 上是增函数，f(-2)=0，求不等式
的解集.例4．已知函数y=f(x)的定义域为R，对任意的x,y都满足f(x+y)=f(x)+f(y),当 x>0时，f(x)>0.
(1)试判断f(x)的奇偶性；
(2)试判断f(x)的单调性，并证明； 1.已知f(x)是定义在（-1，1）上的奇函数，且f(x)在区间（-1，1）上是增函数，求满足 的实数a的取值范围. 作业:2．定义在实数集上的函数f(x)，对任意x，y∈R，
有f(x+y)+f(x-y)=2f(x)·f(y)且f(0)≠0
①求证：f(0)=1　　　
②求证：y=f(x)是偶函数