1.1.2集合间的基本关系

课件15张PPT。1.1.2集合间的
基本关系 实数有相等关系，大小关系，类比
实数之间的关系，集合之间是否具备类
似的关系？知识点[设问]：观察下面几组集合，集合A与集合B具有什么关系？
(1) A={1，2，3}，B={1，2，3，4，5}.
(2) A={x|x>3},B={x|x-2>0}.
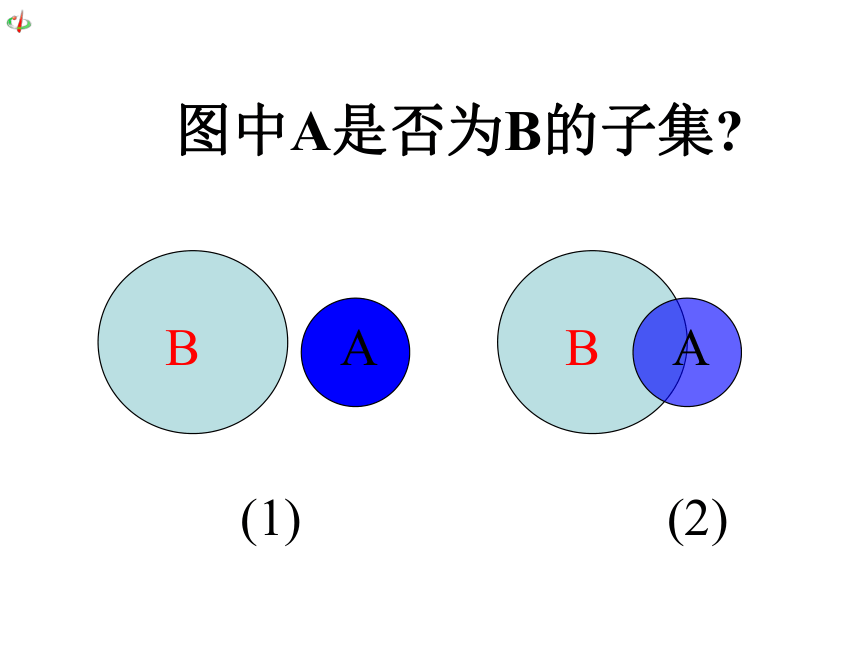
(3)A={x|x是龙港高中高一（7）班的女生}，B={x|x是龙港高中高一（7）班的学生}．1.子 集 一般地，对于两个集合，如果A中任意一个元素都是B的元素，称集合A是集合B的子集，记作A?B.读作“A包含于B”或“B包含A”.这时说集合A是集合B的子集.数学语言：若x∈A，都有x∈B，则A?B. 符号语言：BA图中A是否为B的子集?(1)BA(2)练习1．判断下列集合的关系.
(1) N_____Z; (2) N_____Q;
(3) R_____Z; (4) R_____Q;
(5) A={x| (x-1)2=0}， B={y|y2-3y+2=0};
问题3：观察（6）和（7），集合A与集合B的元素，有何关系？(6) A={-1,1}， B={x|x2-1=0};
(7)A={x|x是两条边相等的三角形} B={x|x是等腰三角形}。若A?B，B?A，则A＝B.2.集合相等定义：一般的，对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时集合B的任何一个元素都是集合A的元素，说集合A等于集合B，记作A=B。3.真子集 如果A?B，但存在元素x∈B，且
x A，称A是B的真子集.
记作A?B，或B?A.规定：空集是任何集合的子集，空集
是任何非空集合的真子集.练习2：在以下六个写法中
①{0}∈{0，1} ②??{0}
③{0，－1，1}?{－1，0，1}
④
⑤??{?}
⑥{(0，0)}＝{0}.
错误个数为 ( )A.3个 B.4个 C.5个 D.6个例1⑴写出集合{a，b}的所有子集；
⑵写出所有{a，b，c}的所有子集；
⑶写出所有{a，b，c，d}的所有子集.例题例2设集合A＝{1, a, b}，B＝{a, a2, ab}，
若A＝B，求实数a， b.例3已知A＝{x | x2－2x－3＝0}, B＝{x | ax－1＝0}, 若B?A, 求实数a的值．变题1：已知M={x|-2 }, N={x|a-1若N M 求a的取值范围
变题2：已知M={x|x2-3x+2=0}, N={x|x2-2x+a-1=0},若N M, 求a的值。
小结：当A ，且集合B已确定时，对集合
A要讨论
①A=Ф ② A≠Ф练习：
(1)已知集合A={x|5若 A B ,求m的取值范围.
(2)设集合A={x||x|2-3|x|+2=0},
B={x|(a-2)x=2},则满足B是A的真子集的a的值共有几个？
思考：若S={x|x= 2n+1, n∈Z}, T={x|x=4k±1, k∈Z}
试判断S与T的关系？
变题：若A={x|x= , n∈Z}

B={x|x=n- n∈Z}
C={x|x= n∈Z}

分析A，B，C之间的关系？ 子集：A?B?任意x∈A? x∈B.
真子集：课堂小结A?B ? x∈A，x∈B，但存在
x0∈A且x0?A.集合相等：A＝B? A?B且B?A.空集：?.性质：①??A，若A非空， 则??A.
②A?A. ③A?B，B?C?A?C.作业：1. 写出满足 的所有集 合A. 2. 设集合 ， ，若 A B，求实数m的值.4.设集合 ， ， 若 ，求实数 的取值范围.