江苏省某重点中学九年级数学上册《图形与证明(二)》章后复习
文档属性
| 名称 | 江苏省某重点中学九年级数学上册《图形与证明(二)》章后复习 |  | |
| 格式 | zip | ||
| 文件大小 | 42.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-16 19:29:38 | ||
图片预览


文档简介
一. 本周教学内容:
图形与证明(二)复习
教学目标:
(1)通过本节课的复习,归纳整理等腰三角形的性质和判定、直角三角形全等判定定
理、角平分线性质定理及逆定理、平行四边形的性质和判定、矩形、菱形、正方形
的性质和判定、等腰梯形的性质和判定、以及三角形、梯形中位线定理。
(2)探索三角形、特殊四边形及中位线的证明规律和方法,提高解题能力。
二. 重点、难点:
重点:梳理各知识要点,探索证明的规律和方法。
难点:探索证明的过程
课堂教学:
(一)知识要点:
1.
2.
3.
4.
5.
【典型例题】
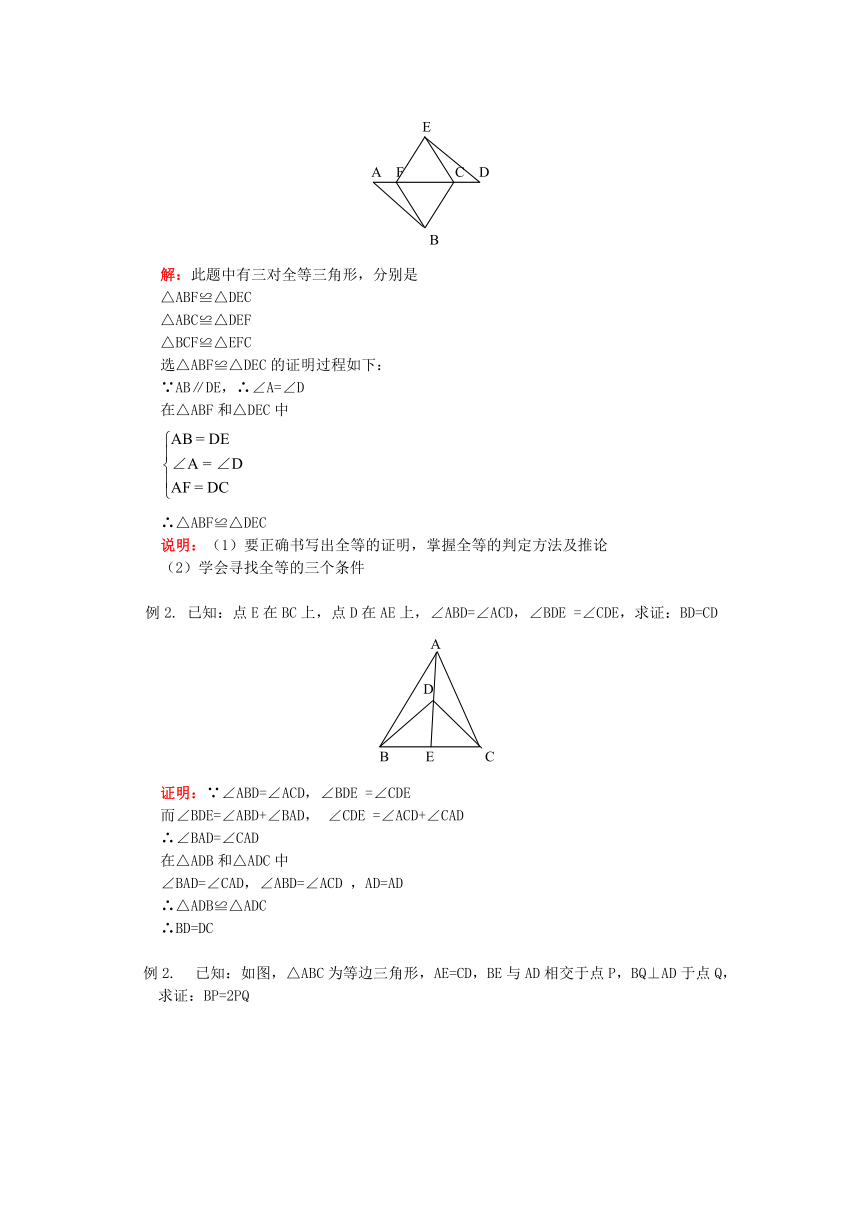
已知:AB//DE,AB=DE,AF=DC,请问图中有哪几对全等三角形?并任选其中一对给 予证明(安徽中考试题)
解:此题中有三对全等三角形,分别是
△ABF≌△DEC
△ABC≌△DEF
△BCF≌△EFC
选△ABF≌△DEC的证明过程如下:
∵AB∥DE,∴∠A=∠D
在△ABF和△DEC中
∴△ABF≌△DEC
说明:(1)要正确书写出全等的证明,掌握全等的判定方法及推论
(2)学会寻找全等的三个条件
例2. 已知:点E在BC上,点D在AE上,∠ABD=∠ACD,∠BDE =∠CDE,求证:BD=CD
证明:∵∠ABD=∠ACD,∠BDE =∠CDE
而∠BDE=∠ABD+∠BAD, ∠CDE =∠ACD+∠CAD
∴∠BAD=∠CAD
在△ADB和△ADC中
∠BAD=∠CAD,∠ABD=∠ACD ,AD=AD
∴△ADB≌△ADC
∴BD=DC
已知:如图,△ABC为等边三角形,AE=CD,BE与AD相交于点P,BQ⊥AD于点Q,
求证:BP=2PQ
证明:∵△ABC是等边三角形
∴∠BAC=∠C=60°,AB=AC
在ABE和CAD中
∵AB=CA,∠BAE=∠C,AE=CD
∴△ABE≌△CAD(SAS)
∴∠ABE=∠CAD
∴∠BPQ=∠ABE+∠BAP=∠CAD+∠BAP=∠BAC=60°
∵BQ⊥AD ,∴∠BQP=90°∴∠PBQ=30°
∴PQ=BP(直角三角形中,如果一个锐角等于30°,那么它所对直角边等于斜边的一
半)即BP=2PQ
例4. 已知:矩形ABCD的对角线AC,BD相交于点O,E、F分别是OA、OB 的中点,求证:
△A DE≌△BCF
证明:∵矩形ABCD,
∴AD=BC,OA=OC,OB=OD
AC=BD,AD∥BC
∴OA=OB=OC,∠DAE=∠OCB=∠OBC
∵E、F分别是OA,OB的中点
∴AE=OA,BF=OB
∵OA=OB
∴AE=BF
∴△ADE≌△BCF(SAS)
例5. 已知:正方形ABCD的对角线AC、BD交于点O,∠OCF=∠OBE,求证:OE=OF。
证明:∵正方形ABCD,∴AC⊥BD
∴∠AOB=∠BOC=90°
OB=OC
又∵∠OCF=∠OBE
∴△OCF≌△OBE
∴OE=OF
例6. 梯形ABCD中,AD∥BC,AB=DC,P为梯形ABCD外一点,PA、PD分别交线段BC于点
E、F,且PA=PD。
(1)写出图中三对全等的三角形(不再添加辅助线)
(2)选择其中一以加以证明。
解:(1)①△ABP≌△DCP,②△ABE≌△DCF ③△BEP≌△CFP
(2)下面就△ABP≌△DCP加以证明
∵AD∥BC,AB=DC
∴梯形ABCD为等腰梯形
∴∠BAD=∠CDA
∵PA=PD
∴∠PAD=∠PDA
∴∠BAD-∠PAD=∠CDA—∠PDA
即∠BAP=∠CDP
在△ABP和△DCP中
∴△ABP≌△DCP
例7. 已知:如图,在△ABC中,AB=BC,D、E、F分别是BC、AC、AB边上的中点。
(1)求证四边形BDEF是菱形。
(2)若AB=12cm,求菱形BDEF的周长。
证明:∵D、E、F分别是BC、AC、AB边上的中点
∴DE∥AB,EF∥BC,DE =AB , EF=BC
∴四边形BDEF是平行四边形
又∵AB=BC
∴DE=EF
∴四边形BDEF是菱形
解:(2)∵AB=12cm, F为AB的中点
∴BF=6cm
∴菱形BDEF的周长为6×4=24(cm)
【模拟试题】(答题时间:40分钟)
一. 选择题
1. 在△ABC与△DEF中,给出以下六个条件:①AB=DE ②BC=EF ③AC=DF ④∠A=∠D
⑤∠ B=∠E ⑥∠C=∠F,以其中三个条件作为已知,不能判断△ABC与△DEF全等的是
( )
A. ①②⑤ B. ①②③ C. ①④⑥ D. ②③④
2. 用两个边长为a的等边三角形纸片拼成的四边形是( )
A. 等腰梯形 B. 正方形 C. 矩形 D. 菱形
3. 用两个全等的直角三角形来拼下列图形①平行四边形(不包括菱形,矩形,正方形) ②
矩形 ③菱形 ④正方形 ⑤等腰三角形,一定可以拼成的图形是( )
A. ①②⑤ B. ②③⑤ C. ①④⑤ D. ①②③
4. A、B、C、D在同一平面内,从①AB=CD ②AB∥CD ③BC∥AD ④BC=AD这四个条件中任
选两个,能使四边形ABCD是平行四边形的选法有( )
A. 3种 B. 4种 C. 5种 D. 6种
5. 矩形两条对角线的夹角中,若钝角为120°,则短边与长边之比为( )
A. 1:2 B. 1: C. 1:3 D. 1:
二. 填空题
6. 矩形ABCD的对角线交于点O,若矩形的周长为68,△AOB与△BOC的周长之差为4,
则矩形的长和宽分别为 。
7. 等腰梯形的两条对角线互相垂直,中位线长为8cm,,则高为 。
8. 在活动课上,小丽已有两根长为4cm,8cm的小木棒,现在打算拼出一个等腰三角形,则
小丽应取的第三根小棒长是 cm。
三. 解答题
9. 如图,将平行四边形ABCD的对角线BD向两个方向延长至E和F,使BE=DF,求证:四
边形AECF是平行四边形。
10. 等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点。
(1)求证:四边形MENF是菱形。
(2)若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,并证
明你的结论。
11. 已知任意四边形ABCD(AB、DC不平行),E、F分别是AB、CD的中点,有人认为线段
EF的取值范围为:|AD-BC|<EF<(AD+BC),你同意吗?说一说你的看法。
12. 已知正方形ABCD中,M是AB的中点,E是AB延长线上的一点,MN垂直于DM且交
∠CBE的平分线于N。
(1)求证:MD=MN
(2)如果将上述条件中“M是AB中点”改为 “M是AB上的任意一点”,其余条件不
变,则结论“MD=MN”还成立吗?如果成立,请证明,如果不成立,请说明理由。
【试题答案】
1. D 2. D 3. A 4. B 5. D
6. 19和15
7. 8cm 8. 8
9. 证明:连接AC交BD于O
∵平行四边形ABCD
∴OA= OC OB=OD
∵BE=DF
∴OE=OF
∴四边形AECF是平行四边形
10. 提示:(1)先利用三角形中位线定理证四边形MENF是平行四边形,再证一组邻边相
等
(2)高是底边BC的一半
11. 同意
提示:连接BD,取BD的中点M,连接ME、MF则ME=AD、MF=BC,再利用三角形边
的不等关系证明。
12. (1)提示:在AD上截取DG=BM,连接MG,证△DGM≌△MBN
(2)成立。在DA上取点G,使DG=BM,连接MG,再证△DGM≌△MBN
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
