2021-2022学年黑龙江省哈尔滨市香坊区八年级(上)期末数学试卷(五四学制)(word解析版)
文档属性
| 名称 | 2021-2022学年黑龙江省哈尔滨市香坊区八年级(上)期末数学试卷(五四学制)(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 906.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览



文档简介
2021-2022学年黑龙江省哈尔滨市香坊区八年级第一学期期末数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.下面的图案中,不是轴对称图形的是( )
A. B. C. D.
2.下列计算一定正确的是( )
A.a2+a2=a4 B.a a4=a4 C.(a2)3=a6 D.a6÷a2=a3
3.若分式的值为0,则实数x的值为( )
A.﹣2 B.﹣1 C.0 D.1
4.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
5.化简结果正确的是( )
A.ab B.﹣ab C.a2﹣b2 D.b2﹣a2
6.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADE关于直线AD对称,点B的对称点是点E,则∠CAE的度数为( )
A.10° B.20° C.30° D.40°
7.如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD,△ABC的周长为26,△ABD的周长为16,则AE的长为( )
A.10 B.8 C.6 D.5
8.在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.(a+2b)(a﹣b)=a2+ab﹣2b2
D.a2﹣b2=(a+b)(a﹣b)
9.甲、乙两种机器人都被用来搬运货物,已知乙型机器人比甲型机器人每小时多搬运600千克,甲型机器人运5000千克所用的时间与乙型机器人搬运8000千克所用的时间相等,设甲型机器人每小时搬运x千克货物,则可列方程为( )
A. B.
C. D.
10.已知xm=a,xn=b,m,n均为正整数,则x2m+n的值为( )
A.2ab B.2a+b C.a2b D.a2+b
二、填空题(每小题3分,共计30分)
11.0.0012用科学记数法表示为 .
12.要使分式有意义,则x应满足的条件是 .
13.计算﹣的结果为 .
14.把3ax2﹣3ay2因式分解的结果是 .
15.计算(x+3)(x+4)﹣2(x+6)的结果为 .
16.若ab≠0,且a+b=5ab,则的值为 .
17.已知长方形的面积为12,其中一边长为,则该长方形的另一边长为 .
18.已知a+b=3,ab=10,则a2+b2的值为 .
19.如图,四边形ABCD中,AD∥BC,连接BD,BD平分∠ABC,E是直线AD上一点,AB=8,DE=2,则AE的长为 .
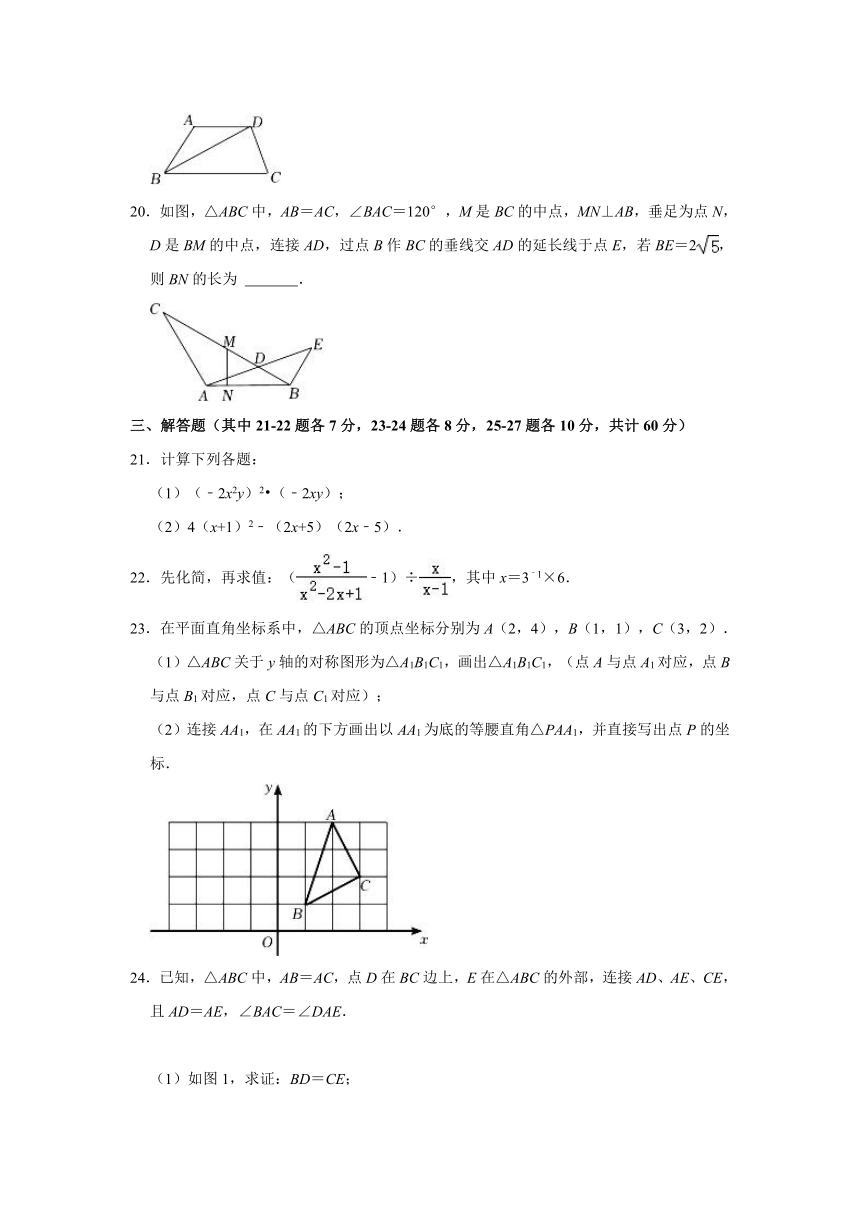
20.如图,△ABC中,AB=AC,∠BAC=120°,M是BC的中点,MN⊥AB,垂足为点N,D是BM的中点,连接AD,过点B作BC的垂线交AD的延长线于点E,若BE=2,则BN的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.计算下列各题:
(1)(﹣2x2y)2 (﹣2xy);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
22.先化简,再求值:(﹣1)÷,其中x=3﹣1×6.
23.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,1),C(3,2).
(1)△ABC关于y轴的对称图形为△A1B1C1,画出△A1B1C1,(点A与点A1对应,点B与点B1对应,点C与点C1对应);
(2)连接AA1,在AA1的下方画出以AA1为底的等腰直角△PAA1,并直接写出点P的坐标.
24.已知,△ABC中,AB=AC,点D在BC边上,E在△ABC的外部,连接AD、AE、CE,且AD=AE,∠BAC=∠DAE.
(1)如图1,求证:BD=CE;
(2)如图2,当∠BAC=108°,AD=BD时,连接DE交AC于点F,如果把顶角为36°的等腰三角形称为黄金三角形,在不添加任何辅助线的情况下,请直接写出图2中四个黄金三角形.
25.某商店第一次用600元购进一款中性笔若干支,第二次又用750元购进该款中性笔,但这次每支中性笔的进价比第一次多1元,所购进的中性笔数量与第一次相同.
(1)求第一次每支中性笔的进价是多少元?
(2)若要求这两次购进的中性笔按同一价格全部销售完毕后获利不低于450元,求每支中性笔售价至少是多少元?
26.已知,△ABC中,∠A+2∠B=180°.
(1)如图1,求证:AB=AC;
(2)如图2,D是△ABC外一点,连接AD、BD,且AB=AD,作∠CAD的平分线交BD于点E,若∠BAC=60°,求∠AED的度数;
(3)如图3,在(2)的条件下,连接CD交AE于点F,若AF=2,BE=3,求DE的长.
27.已知,在平面直角坐标系中,点O为坐标原点,A点坐标为(0,a),B点坐标为(b,0),且满足a2﹣12a+36+=0.
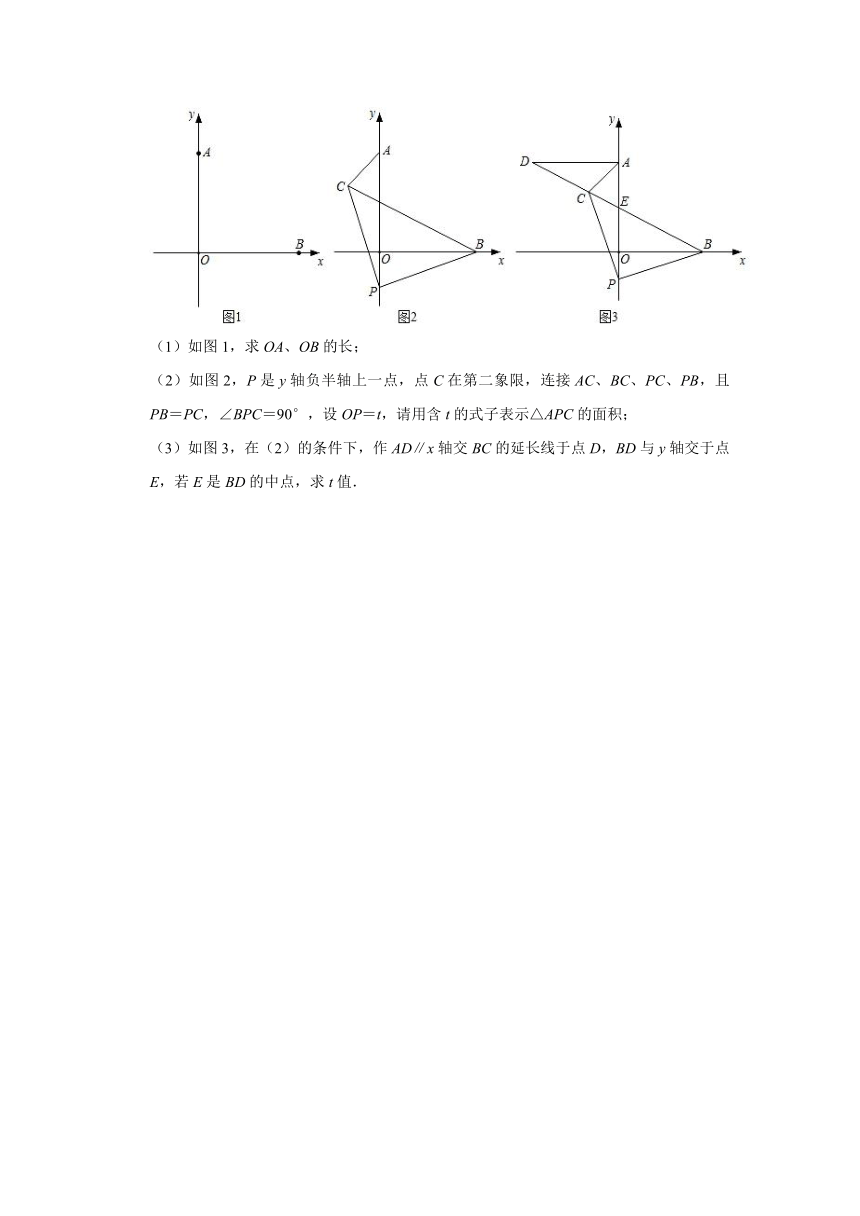
(1)如图1,求OA、OB的长;
(2)如图2,P是y轴负半轴上一点,点C在第二象限,连接AC、BC、PC、PB,且PB=PC,∠BPC=90°,设OP=t,请用含t的式子表示△APC的面积;
(3)如图3,在(2)的条件下,作AD∥x轴交BC的延长线于点D,BD与y轴交于点E,若E是BD的中点,求t值.
参考答案
一、选择题(每小题3分,共计30分)
1.下面的图案中,不是轴对称图形的是( )
A. B. C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:A、是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项符合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不合题意;
故选:B.
2.下列计算一定正确的是( )
A.a2+a2=a4 B.a a4=a4 C.(a2)3=a6 D.a6÷a2=a3
【分析】利用合并同类项的法则,同底数幂的乘法的法则,幂的乘方的法则,同底数幂的除法的法则对各项进行运算即可.
解:A、a2+a2=2a2,故A不符合题意;
B、a a4=a5,故B不符合题意;
C、(a2)3=a6,故C符合题意;
D、a6÷a2=a4,故D不符合题意;
故选:C.
3.若分式的值为0,则实数x的值为( )
A.﹣2 B.﹣1 C.0 D.1
【分析】分式值为零的条件是分子等于零且分母不等于零.
解:分式的值为0,
∴x+2=0且x﹣1≠0,
解得:x=﹣2.
故选:A.
4.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
【分析】利用最简二次根式的定义:被开方数不含分母,分母中不含根号,且被开方数不含能开的尽方的因数,判断即可.
解:A、原式=4,不符合题意;
B、原式=,不符合题意;
C、原式=2,不符合题意;
D、是最简二次根式,符合题意.
故选:D.
5.化简结果正确的是( )
A.ab B.﹣ab C.a2﹣b2 D.b2﹣a2
【分析】首先将分式的分子因式分解,进而约分求出即可.
解:==﹣ab.
故选:B.
6.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADE关于直线AD对称,点B的对称点是点E,则∠CAE的度数为( )
A.10° B.20° C.30° D.40°
【分析】求出∠C,∠AED,利用三角形的外角的性质求解即可.
解:∵∠B=50°,∠ABC=90°,
∴∠C=90°﹣50°=40°,
∵AD⊥BC,△ADB与△ADE关于直线AD对称,
∴∠AED=∠B=50°,
∵∠AED=∠C+∠CAE,
∴∠CAE=50°﹣40°=10°,
故选:A.
7.如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD,△ABC的周长为26,△ABD的周长为16,则AE的长为( )
A.10 B.8 C.6 D.5
【分析】根据线段垂直平分线的性质得到AE=AC,AD=CD,根据三角形的周长得到AC=26﹣16=10,于是得到结论.
解:∵AC的垂直平分线交BC于点D,
∴AE=AC,AD=CD,
∵△ABC的周长=AC+BC+AB=26,△ABD的周长=AB+AD+BD=AB+BC=16,
∴AC=26﹣16=10,
∴AE=AC=5,
故选:D.
8.在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.(a+2b)(a﹣b)=a2+ab﹣2b2
D.a2﹣b2=(a+b)(a﹣b)
【分析】图甲中阴影部分的面积为两正方形的面积之差,即为a2﹣b2,图乙中阴影部分为边长分别为(a+b)和(a﹣b),其面积为(a+b)(a﹣b),利用据两个图形中阴影部分的面积相等即可得到平方差公式.
解:∵图甲中阴影部分的面积=a2﹣b2,图乙中阴影部分的面积=(a+b)(a﹣b),
而两个图形中阴影部分的面积相等,
∴a2﹣b2=(a+b)(a﹣b).
故选:D.
9.甲、乙两种机器人都被用来搬运货物,已知乙型机器人比甲型机器人每小时多搬运600千克,甲型机器人运5000千克所用的时间与乙型机器人搬运8000千克所用的时间相等,设甲型机器人每小时搬运x千克货物,则可列方程为( )
A. B.
C. D.
【分析】设甲型机器人每小时搬运x千克,则乙型机器人每小时搬运(x+600)千克,根据工作时间=工作总量÷工作效率结合甲型机器人搬运5000千克所用的时间与乙型机器人搬运8000千克所用的时间相同,即可得出关于x的分式方程,此题得解.
解:设甲型机器人每小时搬运x千克,则乙型机器人每小时搬运(x+600)千克,
依题意,得:=.
故选:B.
10.已知xm=a,xn=b,m,n均为正整数,则x2m+n的值为( )
A.2ab B.2a+b C.a2b D.a2+b
【分析】逆向运用同底数幂的乘法法则以及利用幂的乘方运算法则解答即可.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加;幂的乘方法则:底数不变,指数相乘.
解:∵xm=a,xn=b,m,n均为正整数,
∴x2m+n=x2m xn=(xm)2 xn=a2b.
故选:C.
二、填空题(每小题3分,共计30分)
11.0.0012用科学记数法表示为 1.2×10﹣3 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:将0.0012用科学记数法表示为1.2×10﹣3,
故答案是:1.2×10﹣3.
12.要使分式有意义,则x应满足的条件是 x≠2 .
【分析】直接利用分式有意义则分母不等于零,进而得出答案.
解:∵分式有意义,
∴x﹣2≠0,
解得:x≠2.
故答案为:x≠2.
13.计算﹣的结果为 ﹣ .
【分析】直接利用二次根式的性质化简,再利用二次根式的加减运算法则计算即可.
解:原式=2﹣3
=﹣.
故答案为:﹣.
14.把3ax2﹣3ay2因式分解的结果是 3a(x﹣y)(x+y) .
【分析】先题3a,然后把x2﹣y2用平方差公式分解即可.
解:原式=3a(x2﹣y2)=3a(x﹣y)(x+y).
故答案为3a(x﹣y)(x+y).
15.计算(x+3)(x+4)﹣2(x+6)的结果为 x2+5x .
【分析】利用多项式乘多项式的法则及去括号的法则对所求的式子进行运算即可.
解:(x+3)(x+4)﹣2(x+6)
=x2+4x+3x+12﹣2x﹣12
=x2+5x.
故答案为:x2+5x.
16.若ab≠0,且a+b=5ab,则的值为 5 .
【分析】将a+b=5ab代入+=+=计算即可.
解:∵a+b=5ab,
∴+=+
=
=
=5,
故答案为:5.
17.已知长方形的面积为12,其中一边长为,则该长方形的另一边长为 3 .
【分析】直接利用二次根式的除法运算法则计算得出答案.
解:∵长方形的面积为12,其中一边长为,
∴该长方形的另一边长为:12÷2=3.
故答案为:3.
18.已知a+b=3,ab=10,则a2+b2的值为 25 .
【分析】由完全平方公式(a+b)2=a2+2ab+b2变形为a2+b2=(a+b)2﹣2ab后,就可以代入计算了.
解:∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab=(3)2﹣2×10=45﹣20=25,
故答案为:25.
19.如图,四边形ABCD中,AD∥BC,连接BD,BD平分∠ABC,E是直线AD上一点,AB=8,DE=2,则AE的长为 6或10 .
【分析】根据平行线的性质得到∠ADB=∠DBC,根据角平分线的定义得到∠ABD=∠CBD,求得∠ABD=∠ADB,得到AD=AB=8,根据线段的和差即可得到结论.
解:∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB=8,
∵E是直线AD上一点,DE=2,
∴AE=AD﹣DE=8﹣2=6或AE=AD+DE=8+2=10,
∴AE的长为6或10,
故答案为:6或10.
20.如图,△ABC中,AB=AC,∠BAC=120°,M是BC的中点,MN⊥AB,垂足为点N,D是BM的中点,连接AD,过点B作BC的垂线交AD的延长线于点E,若BE=2,则BN的长为 .
【分析】连接AM,根据等腰三角形的性质及含30°角的直角三角形的性质可求得AB=2AM,再证明△AMD≌△EBD可求得AM及AB的长,由勾股定理可求BM的长,进而利用含30° 角的直角三角形的性质及勾股定理可求解BN的长.
解:连接AM,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠C=30°,
∵M为BC的中点,
∴AM⊥BC,
∴AB=2AM,
∵BE⊥BC,
∴∠AMD=∠EBD=90°,
∵D为BM的中点,
∴DM=DB,
在△AMD和△EBD中,
∠AMD=∠EBD,DM=DB,∠ADM=∠EDB,
∴△AMD≌△EBD(ASA),
∴AM=BE=,
∴AB=,
∴BM=,
∵MN⊥AB,∠B=30°,
∴MN=BM=,
∴BN=.
故答案为:.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.计算下列各题:
(1)(﹣2x2y)2 (﹣2xy);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
【分析】(1)直接利用积的乘方运算法则化简,再利用单项式乘单项式计算得出答案;
(2)直接利用完全平方公式以及平方差公式化简,进而合并同类项得出答案.
解:(1)(﹣2x2y)2 (﹣2xy)
=4x4y2 (﹣2xy)
=﹣8x5y3;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
22.先化简,再求值:(﹣1)÷,其中x=3﹣1×6.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再由负整数指数幂计算出x的值,代入计算即可.
解:原式=[﹣1]
=(﹣)
=
=,
当x=3﹣1×6=×6=2时,
原式==1.
23.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,1),C(3,2).
(1)△ABC关于y轴的对称图形为△A1B1C1,画出△A1B1C1,(点A与点A1对应,点B与点B1对应,点C与点C1对应);
(2)连接AA1,在AA1的下方画出以AA1为底的等腰直角△PAA1,并直接写出点P的坐标.
【分析】(1)利用轴对称的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)根据等腰直角三角形的定义作出图形.
解:(1)如图,△A1B1C1即为所求;
(2)如图,△PAA1即为所求,P(0,2).
24.已知,△ABC中,AB=AC,点D在BC边上,E在△ABC的外部,连接AD、AE、CE,且AD=AE,∠BAC=∠DAE.
(1)如图1,求证:BD=CE;
(2)如图2,当∠BAC=108°,AD=BD时,连接DE交AC于点F,如果把顶角为36°的等腰三角形称为黄金三角形,在不添加任何辅助线的情况下,请直接写出图2中四个黄金三角形.
【分析】(1)根据∠BAC=∠DAE,可得∠BAD=∠CAE,然后再证明△ABD≌△ACE即可;
(2)根据题目的已知条件并结合图形,易证△CAD,△ADF,△DCE,△CEF都是顶角为36°的等腰三角形.
【解答】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)解:∵AB=AC,AD=AE,∠BAC=∠DAE=108°,
∴∠B=∠ACB=36°,∠ADE=∠AED=36°,
∵AD=BD,
∴∠B=∠BAD=36°,
∴∠DAC=∠BAC﹣∠BAD=108°﹣36°=72°,
∴∠ADC=180°﹣∠ACB﹣∠DAC=72°,
∴CA=CD,
∴△CAD是黄金三角形,
∵∠ADE=36°,∠DAC=72°,
∴∠AFD=180°﹣∠ADE﹣∠DAC=72°,
∴DA=DF,
∴△DAF是黄金三角形,
由(1)得:△ABD≌△ACE,
∴∠B=∠ACE=36°,
∵∠AFD=∠CFE=72°,
∴∠DEC=180°﹣∠CFE﹣∠ACE=72°,
∴CF=CE,
∴△CFE是黄金三角形,
∵∠ADC=72°,∠ADF=36°,
∴∠CDF=∠ADC﹣∠ADF=36°,
∴∠DCE=180°﹣∠CDF﹣∠DEC=72°,
∴DC=DE,
∴△CDE是黄金三角形,
∴△CAD,△ADF,△DCE,△CEF都是黄金三角形.
25.某商店第一次用600元购进一款中性笔若干支,第二次又用750元购进该款中性笔,但这次每支中性笔的进价比第一次多1元,所购进的中性笔数量与第一次相同.
(1)求第一次每支中性笔的进价是多少元?
(2)若要求这两次购进的中性笔按同一价格全部销售完毕后获利不低于450元,求每支中性笔售价至少是多少元?
【分析】(1)设第一次每支中性笔的进价是x元,则第二次每支中性笔的进价是(x+1)元,根据两次购进中性笔的数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)利用数量=总价÷单价可求出第一次购进中性笔的数量,进而可得出第二次购进中性笔的数量,设每支中性笔售价为y元,根据两次购进的中性笔全部销售完毕后获利不低于450元,即可得出关于y的一元一次不等式,解之取其中的最小值即可得出结论.
解:(1)设第一次每支中性笔的进价是x元,则第二次每支中性笔的进价是(x+1)元,
依题意得:=,
解得:x=4,
经检验,x=4是原方程的解且符合题意.
答:第一次每支中性笔的进价是4元.
(2)第一次购进中性笔的数量为600÷4=150(支),
∴第二次购进中性笔150支.
设每支中性笔售价为y元,
依题意得:(150+150)y﹣600﹣750≥450,
解得:y≥6.
答:每支中性笔售价至少是6元.
26.已知,△ABC中,∠A+2∠B=180°.
(1)如图1,求证:AB=AC;
(2)如图2,D是△ABC外一点,连接AD、BD,且AB=AD,作∠CAD的平分线交BD于点E,若∠BAC=60°,求∠AED的度数;
(3)如图3,在(2)的条件下,连接CD交AE于点F,若AF=2,BE=3,求DE的长.
【分析】(1)欲证明AB=AC,只要证明∠B=∠C即可;
(2)如图2中,连接CD交AE于点T,连接EC.设∠BAD=x.证明∠CDB=30°,AE⊥CD,可得结论;
(3)如图3中,连接CE,在CE上取一点R,使得AR=AE.首先证明△AER时等边三角形,再证明△AEB≌△ARC(SAS),推出BE=CR=3,设EF=x,则AE=ER=x+2,DE=EC=x+2+3=x+5,证明DE=2x,构建方程求解即可.
【解答】(1)证明:∵∠A+∠B+∠C=180°,∠A+2∠B=180°,
∴∠B=∠C,
∴AB=AC;
(2)解:如图2在,连接CD交AE于点T,连接EC.设∠BAD=x.
∵AB=AC=AD,
∴∠ADC=∠ACD=(180°﹣x﹣60°)=60°﹣x,∠ADB=∠ABD=(180°﹣x)=90°﹣x,
∴∠CDB=∠ADB﹣∠ADC=90°﹣x﹣(60°﹣x)=30°,
∵AD=AC,AE平分∠DAC,
∴AE⊥CD,
∴∠DTE=90°,
∴∠AED=90°﹣30°=60°;
(3)如图3中,连接CE,在CE上起一点R,使得AR=AE.
在△AED和△AEC中,
,
∴△AED≌△AEC(SAS),
∴∠AED=∠AEC=60°,DE=EC,
∵AE=AR,
∴△AER时等边三角形,
∴AE=ER,∠EAR=60°,
∵∠EAR=∠BAC=60°,
∴∠EAB=∠RAC,
∵AE=AR,AB=AC,
∴△AEB≌△ARC(SAS),
∴BE=CR=3,
设EF=x,则AE=ER=x+2,DE=EC=x+2+3=x+5,
∵∠DFE=90°,∠EDF=30°,
∴DE=2EF=2x,
∴2x=x+5,
∴x=5,
∴DE=2x=10.
27.已知,在平面直角坐标系中,点O为坐标原点,A点坐标为(0,a),B点坐标为(b,0),且满足a2﹣12a+36+=0.
(1)如图1,求OA、OB的长;
(2)如图2,P是y轴负半轴上一点,点C在第二象限,连接AC、BC、PC、PB,且PB=PC,∠BPC=90°,设OP=t,请用含t的式子表示△APC的面积;
(3)如图3,在(2)的条件下,作AD∥x轴交BC的延长线于点D,BD与y轴交于点E,若E是BD的中点,求t值.
【分析】(1)利用非负数的性质求出a,b的值可得结论;
(2)如图2中,过点C作CH⊥AP于点H.证明△PHC≌△BOP(AAS),推出CH=OP=t,可得结论;
(3)证明△ADE≌△OBE(ASA),推出AD=OB=6,AE=EO=3,由△PHC≌△BOP,推出PH=OB=OA=6,推出AH=OP=t,EH=3﹣t,由CH∥AD,推出=,可得=,解方程即可解决问题.
解:(1)∵a2﹣12a+36+=0,
∴(a﹣6)2+=0,
又∵(a﹣6)2≥0,≥0,
∴a=b=6,
∴A(0,6),B(6,0),
∴OA=OB=6;
(2)如图2中,过点C作CH⊥AP于点H.
∵∠BPC=∠CHP=∠BOP=90°,
∴∠CPH+∠BPO=90°,∠BPO+∠OBP=90°,
∴∠CPH=∠PBO,
∵PC=PB,
∴△PHC≌△BOP(AAS),
∴CH=OP=t,
∵AP=PO+OA=t+6,
∴S△ACP= AP CH=×(t+6)×t=t2+3t(t<0);
(3)如图3在,过点C作CH⊥OA于点H.
∵AD∥OB,
∴∠D=∠OBE,
∵∠AED=∠BEO,DE=EB,
∴△ADE≌△OBE(ASA),
∴AD=OB=6,AE=EO=3,
∵△PHC≌△BOP,
∴PH=OB=OA=6,
∴AH=OP=t,
∴EH=3﹣t,
∵CH∥AD,
∴=,
∴=,
解得t=2.
一、选择题(每小题3分,共计30分)
1.下面的图案中,不是轴对称图形的是( )
A. B. C. D.
2.下列计算一定正确的是( )
A.a2+a2=a4 B.a a4=a4 C.(a2)3=a6 D.a6÷a2=a3
3.若分式的值为0,则实数x的值为( )
A.﹣2 B.﹣1 C.0 D.1
4.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
5.化简结果正确的是( )
A.ab B.﹣ab C.a2﹣b2 D.b2﹣a2
6.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADE关于直线AD对称,点B的对称点是点E,则∠CAE的度数为( )
A.10° B.20° C.30° D.40°
7.如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD,△ABC的周长为26,△ABD的周长为16,则AE的长为( )
A.10 B.8 C.6 D.5
8.在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.(a+2b)(a﹣b)=a2+ab﹣2b2
D.a2﹣b2=(a+b)(a﹣b)
9.甲、乙两种机器人都被用来搬运货物,已知乙型机器人比甲型机器人每小时多搬运600千克,甲型机器人运5000千克所用的时间与乙型机器人搬运8000千克所用的时间相等,设甲型机器人每小时搬运x千克货物,则可列方程为( )
A. B.
C. D.
10.已知xm=a,xn=b,m,n均为正整数,则x2m+n的值为( )
A.2ab B.2a+b C.a2b D.a2+b
二、填空题(每小题3分,共计30分)
11.0.0012用科学记数法表示为 .
12.要使分式有意义,则x应满足的条件是 .
13.计算﹣的结果为 .
14.把3ax2﹣3ay2因式分解的结果是 .
15.计算(x+3)(x+4)﹣2(x+6)的结果为 .
16.若ab≠0,且a+b=5ab,则的值为 .
17.已知长方形的面积为12,其中一边长为,则该长方形的另一边长为 .
18.已知a+b=3,ab=10,则a2+b2的值为 .
19.如图,四边形ABCD中,AD∥BC,连接BD,BD平分∠ABC,E是直线AD上一点,AB=8,DE=2,则AE的长为 .
20.如图,△ABC中,AB=AC,∠BAC=120°,M是BC的中点,MN⊥AB,垂足为点N,D是BM的中点,连接AD,过点B作BC的垂线交AD的延长线于点E,若BE=2,则BN的长为 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.计算下列各题:
(1)(﹣2x2y)2 (﹣2xy);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
22.先化简,再求值:(﹣1)÷,其中x=3﹣1×6.
23.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,1),C(3,2).
(1)△ABC关于y轴的对称图形为△A1B1C1,画出△A1B1C1,(点A与点A1对应,点B与点B1对应,点C与点C1对应);
(2)连接AA1,在AA1的下方画出以AA1为底的等腰直角△PAA1,并直接写出点P的坐标.
24.已知,△ABC中,AB=AC,点D在BC边上,E在△ABC的外部,连接AD、AE、CE,且AD=AE,∠BAC=∠DAE.
(1)如图1,求证:BD=CE;
(2)如图2,当∠BAC=108°,AD=BD时,连接DE交AC于点F,如果把顶角为36°的等腰三角形称为黄金三角形,在不添加任何辅助线的情况下,请直接写出图2中四个黄金三角形.
25.某商店第一次用600元购进一款中性笔若干支,第二次又用750元购进该款中性笔,但这次每支中性笔的进价比第一次多1元,所购进的中性笔数量与第一次相同.
(1)求第一次每支中性笔的进价是多少元?
(2)若要求这两次购进的中性笔按同一价格全部销售完毕后获利不低于450元,求每支中性笔售价至少是多少元?
26.已知,△ABC中,∠A+2∠B=180°.
(1)如图1,求证:AB=AC;
(2)如图2,D是△ABC外一点,连接AD、BD,且AB=AD,作∠CAD的平分线交BD于点E,若∠BAC=60°,求∠AED的度数;
(3)如图3,在(2)的条件下,连接CD交AE于点F,若AF=2,BE=3,求DE的长.
27.已知,在平面直角坐标系中,点O为坐标原点,A点坐标为(0,a),B点坐标为(b,0),且满足a2﹣12a+36+=0.
(1)如图1,求OA、OB的长;
(2)如图2,P是y轴负半轴上一点,点C在第二象限,连接AC、BC、PC、PB,且PB=PC,∠BPC=90°,设OP=t,请用含t的式子表示△APC的面积;
(3)如图3,在(2)的条件下,作AD∥x轴交BC的延长线于点D,BD与y轴交于点E,若E是BD的中点,求t值.
参考答案
一、选择题(每小题3分,共计30分)
1.下面的图案中,不是轴对称图形的是( )
A. B. C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:A、是轴对称图形,故此选项不合题意;
B、不是轴对称图形,故此选项符合题意;
C、是轴对称图形,故此选项不合题意;
D、是轴对称图形,故此选项不合题意;
故选:B.
2.下列计算一定正确的是( )
A.a2+a2=a4 B.a a4=a4 C.(a2)3=a6 D.a6÷a2=a3
【分析】利用合并同类项的法则,同底数幂的乘法的法则,幂的乘方的法则,同底数幂的除法的法则对各项进行运算即可.
解:A、a2+a2=2a2,故A不符合题意;
B、a a4=a5,故B不符合题意;
C、(a2)3=a6,故C符合题意;
D、a6÷a2=a4,故D不符合题意;
故选:C.
3.若分式的值为0,则实数x的值为( )
A.﹣2 B.﹣1 C.0 D.1
【分析】分式值为零的条件是分子等于零且分母不等于零.
解:分式的值为0,
∴x+2=0且x﹣1≠0,
解得:x=﹣2.
故选:A.
4.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
【分析】利用最简二次根式的定义:被开方数不含分母,分母中不含根号,且被开方数不含能开的尽方的因数,判断即可.
解:A、原式=4,不符合题意;
B、原式=,不符合题意;
C、原式=2,不符合题意;
D、是最简二次根式,符合题意.
故选:D.
5.化简结果正确的是( )
A.ab B.﹣ab C.a2﹣b2 D.b2﹣a2
【分析】首先将分式的分子因式分解,进而约分求出即可.
解:==﹣ab.
故选:B.
6.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADE关于直线AD对称,点B的对称点是点E,则∠CAE的度数为( )
A.10° B.20° C.30° D.40°
【分析】求出∠C,∠AED,利用三角形的外角的性质求解即可.
解:∵∠B=50°,∠ABC=90°,
∴∠C=90°﹣50°=40°,
∵AD⊥BC,△ADB与△ADE关于直线AD对称,
∴∠AED=∠B=50°,
∵∠AED=∠C+∠CAE,
∴∠CAE=50°﹣40°=10°,
故选:A.
7.如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,连接AD,△ABC的周长为26,△ABD的周长为16,则AE的长为( )
A.10 B.8 C.6 D.5
【分析】根据线段垂直平分线的性质得到AE=AC,AD=CD,根据三角形的周长得到AC=26﹣16=10,于是得到结论.
解:∵AC的垂直平分线交BC于点D,
∴AE=AC,AD=CD,
∵△ABC的周长=AC+BC+AB=26,△ABD的周长=AB+AD+BD=AB+BC=16,
∴AC=26﹣16=10,
∴AE=AC=5,
故选:D.
8.在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图1),把余下的部分拼成一个长方形(如图2),根据两个图形中阴影部分的面积相等,可以验证( )
A.(a+b)2=a2+2ab+b2
B.(a﹣b)2=a2﹣2ab+b2
C.(a+2b)(a﹣b)=a2+ab﹣2b2
D.a2﹣b2=(a+b)(a﹣b)
【分析】图甲中阴影部分的面积为两正方形的面积之差,即为a2﹣b2,图乙中阴影部分为边长分别为(a+b)和(a﹣b),其面积为(a+b)(a﹣b),利用据两个图形中阴影部分的面积相等即可得到平方差公式.
解:∵图甲中阴影部分的面积=a2﹣b2,图乙中阴影部分的面积=(a+b)(a﹣b),
而两个图形中阴影部分的面积相等,
∴a2﹣b2=(a+b)(a﹣b).
故选:D.
9.甲、乙两种机器人都被用来搬运货物,已知乙型机器人比甲型机器人每小时多搬运600千克,甲型机器人运5000千克所用的时间与乙型机器人搬运8000千克所用的时间相等,设甲型机器人每小时搬运x千克货物,则可列方程为( )
A. B.
C. D.
【分析】设甲型机器人每小时搬运x千克,则乙型机器人每小时搬运(x+600)千克,根据工作时间=工作总量÷工作效率结合甲型机器人搬运5000千克所用的时间与乙型机器人搬运8000千克所用的时间相同,即可得出关于x的分式方程,此题得解.
解:设甲型机器人每小时搬运x千克,则乙型机器人每小时搬运(x+600)千克,
依题意,得:=.
故选:B.
10.已知xm=a,xn=b,m,n均为正整数,则x2m+n的值为( )
A.2ab B.2a+b C.a2b D.a2+b
【分析】逆向运用同底数幂的乘法法则以及利用幂的乘方运算法则解答即可.同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加;幂的乘方法则:底数不变,指数相乘.
解:∵xm=a,xn=b,m,n均为正整数,
∴x2m+n=x2m xn=(xm)2 xn=a2b.
故选:C.
二、填空题(每小题3分,共计30分)
11.0.0012用科学记数法表示为 1.2×10﹣3 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:将0.0012用科学记数法表示为1.2×10﹣3,
故答案是:1.2×10﹣3.
12.要使分式有意义,则x应满足的条件是 x≠2 .
【分析】直接利用分式有意义则分母不等于零,进而得出答案.
解:∵分式有意义,
∴x﹣2≠0,
解得:x≠2.
故答案为:x≠2.
13.计算﹣的结果为 ﹣ .
【分析】直接利用二次根式的性质化简,再利用二次根式的加减运算法则计算即可.
解:原式=2﹣3
=﹣.
故答案为:﹣.
14.把3ax2﹣3ay2因式分解的结果是 3a(x﹣y)(x+y) .
【分析】先题3a,然后把x2﹣y2用平方差公式分解即可.
解:原式=3a(x2﹣y2)=3a(x﹣y)(x+y).
故答案为3a(x﹣y)(x+y).
15.计算(x+3)(x+4)﹣2(x+6)的结果为 x2+5x .
【分析】利用多项式乘多项式的法则及去括号的法则对所求的式子进行运算即可.
解:(x+3)(x+4)﹣2(x+6)
=x2+4x+3x+12﹣2x﹣12
=x2+5x.
故答案为:x2+5x.
16.若ab≠0,且a+b=5ab,则的值为 5 .
【分析】将a+b=5ab代入+=+=计算即可.
解:∵a+b=5ab,
∴+=+
=
=
=5,
故答案为:5.
17.已知长方形的面积为12,其中一边长为,则该长方形的另一边长为 3 .
【分析】直接利用二次根式的除法运算法则计算得出答案.
解:∵长方形的面积为12,其中一边长为,
∴该长方形的另一边长为:12÷2=3.
故答案为:3.
18.已知a+b=3,ab=10,则a2+b2的值为 25 .
【分析】由完全平方公式(a+b)2=a2+2ab+b2变形为a2+b2=(a+b)2﹣2ab后,就可以代入计算了.
解:∵(a+b)2=a2+2ab+b2,
∴a2+b2=(a+b)2﹣2ab=(3)2﹣2×10=45﹣20=25,
故答案为:25.
19.如图,四边形ABCD中,AD∥BC,连接BD,BD平分∠ABC,E是直线AD上一点,AB=8,DE=2,则AE的长为 6或10 .
【分析】根据平行线的性质得到∠ADB=∠DBC,根据角平分线的定义得到∠ABD=∠CBD,求得∠ABD=∠ADB,得到AD=AB=8,根据线段的和差即可得到结论.
解:∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ABD=∠ADB,
∴AD=AB=8,
∵E是直线AD上一点,DE=2,
∴AE=AD﹣DE=8﹣2=6或AE=AD+DE=8+2=10,
∴AE的长为6或10,
故答案为:6或10.
20.如图,△ABC中,AB=AC,∠BAC=120°,M是BC的中点,MN⊥AB,垂足为点N,D是BM的中点,连接AD,过点B作BC的垂线交AD的延长线于点E,若BE=2,则BN的长为 .
【分析】连接AM,根据等腰三角形的性质及含30°角的直角三角形的性质可求得AB=2AM,再证明△AMD≌△EBD可求得AM及AB的长,由勾股定理可求BM的长,进而利用含30° 角的直角三角形的性质及勾股定理可求解BN的长.
解:连接AM,
∵AB=AC,∠BAC=120°,
∴∠ABC=∠C=30°,
∵M为BC的中点,
∴AM⊥BC,
∴AB=2AM,
∵BE⊥BC,
∴∠AMD=∠EBD=90°,
∵D为BM的中点,
∴DM=DB,
在△AMD和△EBD中,
∠AMD=∠EBD,DM=DB,∠ADM=∠EDB,
∴△AMD≌△EBD(ASA),
∴AM=BE=,
∴AB=,
∴BM=,
∵MN⊥AB,∠B=30°,
∴MN=BM=,
∴BN=.
故答案为:.
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.计算下列各题:
(1)(﹣2x2y)2 (﹣2xy);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
【分析】(1)直接利用积的乘方运算法则化简,再利用单项式乘单项式计算得出答案;
(2)直接利用完全平方公式以及平方差公式化简,进而合并同类项得出答案.
解:(1)(﹣2x2y)2 (﹣2xy)
=4x4y2 (﹣2xy)
=﹣8x5y3;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
22.先化简,再求值:(﹣1)÷,其中x=3﹣1×6.
【分析】先根据分式的混合运算顺序和运算法则化简原式,再由负整数指数幂计算出x的值,代入计算即可.
解:原式=[﹣1]
=(﹣)
=
=,
当x=3﹣1×6=×6=2时,
原式==1.
23.在平面直角坐标系中,△ABC的顶点坐标分别为A(2,4),B(1,1),C(3,2).
(1)△ABC关于y轴的对称图形为△A1B1C1,画出△A1B1C1,(点A与点A1对应,点B与点B1对应,点C与点C1对应);
(2)连接AA1,在AA1的下方画出以AA1为底的等腰直角△PAA1,并直接写出点P的坐标.
【分析】(1)利用轴对称的性质分别作出A,B,C的对应点A1,B1,C1即可;
(2)根据等腰直角三角形的定义作出图形.
解:(1)如图,△A1B1C1即为所求;
(2)如图,△PAA1即为所求,P(0,2).
24.已知,△ABC中,AB=AC,点D在BC边上,E在△ABC的外部,连接AD、AE、CE,且AD=AE,∠BAC=∠DAE.
(1)如图1,求证:BD=CE;
(2)如图2,当∠BAC=108°,AD=BD时,连接DE交AC于点F,如果把顶角为36°的等腰三角形称为黄金三角形,在不添加任何辅助线的情况下,请直接写出图2中四个黄金三角形.
【分析】(1)根据∠BAC=∠DAE,可得∠BAD=∠CAE,然后再证明△ABD≌△ACE即可;
(2)根据题目的已知条件并结合图形,易证△CAD,△ADF,△DCE,△CEF都是顶角为36°的等腰三角形.
【解答】(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)解:∵AB=AC,AD=AE,∠BAC=∠DAE=108°,
∴∠B=∠ACB=36°,∠ADE=∠AED=36°,
∵AD=BD,
∴∠B=∠BAD=36°,
∴∠DAC=∠BAC﹣∠BAD=108°﹣36°=72°,
∴∠ADC=180°﹣∠ACB﹣∠DAC=72°,
∴CA=CD,
∴△CAD是黄金三角形,
∵∠ADE=36°,∠DAC=72°,
∴∠AFD=180°﹣∠ADE﹣∠DAC=72°,
∴DA=DF,
∴△DAF是黄金三角形,
由(1)得:△ABD≌△ACE,
∴∠B=∠ACE=36°,
∵∠AFD=∠CFE=72°,
∴∠DEC=180°﹣∠CFE﹣∠ACE=72°,
∴CF=CE,
∴△CFE是黄金三角形,
∵∠ADC=72°,∠ADF=36°,
∴∠CDF=∠ADC﹣∠ADF=36°,
∴∠DCE=180°﹣∠CDF﹣∠DEC=72°,
∴DC=DE,
∴△CDE是黄金三角形,
∴△CAD,△ADF,△DCE,△CEF都是黄金三角形.
25.某商店第一次用600元购进一款中性笔若干支,第二次又用750元购进该款中性笔,但这次每支中性笔的进价比第一次多1元,所购进的中性笔数量与第一次相同.
(1)求第一次每支中性笔的进价是多少元?
(2)若要求这两次购进的中性笔按同一价格全部销售完毕后获利不低于450元,求每支中性笔售价至少是多少元?
【分析】(1)设第一次每支中性笔的进价是x元,则第二次每支中性笔的进价是(x+1)元,根据两次购进中性笔的数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)利用数量=总价÷单价可求出第一次购进中性笔的数量,进而可得出第二次购进中性笔的数量,设每支中性笔售价为y元,根据两次购进的中性笔全部销售完毕后获利不低于450元,即可得出关于y的一元一次不等式,解之取其中的最小值即可得出结论.
解:(1)设第一次每支中性笔的进价是x元,则第二次每支中性笔的进价是(x+1)元,
依题意得:=,
解得:x=4,
经检验,x=4是原方程的解且符合题意.
答:第一次每支中性笔的进价是4元.
(2)第一次购进中性笔的数量为600÷4=150(支),
∴第二次购进中性笔150支.
设每支中性笔售价为y元,
依题意得:(150+150)y﹣600﹣750≥450,
解得:y≥6.
答:每支中性笔售价至少是6元.
26.已知,△ABC中,∠A+2∠B=180°.
(1)如图1,求证:AB=AC;
(2)如图2,D是△ABC外一点,连接AD、BD,且AB=AD,作∠CAD的平分线交BD于点E,若∠BAC=60°,求∠AED的度数;
(3)如图3,在(2)的条件下,连接CD交AE于点F,若AF=2,BE=3,求DE的长.
【分析】(1)欲证明AB=AC,只要证明∠B=∠C即可;
(2)如图2中,连接CD交AE于点T,连接EC.设∠BAD=x.证明∠CDB=30°,AE⊥CD,可得结论;
(3)如图3中,连接CE,在CE上取一点R,使得AR=AE.首先证明△AER时等边三角形,再证明△AEB≌△ARC(SAS),推出BE=CR=3,设EF=x,则AE=ER=x+2,DE=EC=x+2+3=x+5,证明DE=2x,构建方程求解即可.
【解答】(1)证明:∵∠A+∠B+∠C=180°,∠A+2∠B=180°,
∴∠B=∠C,
∴AB=AC;
(2)解:如图2在,连接CD交AE于点T,连接EC.设∠BAD=x.
∵AB=AC=AD,
∴∠ADC=∠ACD=(180°﹣x﹣60°)=60°﹣x,∠ADB=∠ABD=(180°﹣x)=90°﹣x,
∴∠CDB=∠ADB﹣∠ADC=90°﹣x﹣(60°﹣x)=30°,
∵AD=AC,AE平分∠DAC,
∴AE⊥CD,
∴∠DTE=90°,
∴∠AED=90°﹣30°=60°;
(3)如图3中,连接CE,在CE上起一点R,使得AR=AE.
在△AED和△AEC中,
,
∴△AED≌△AEC(SAS),
∴∠AED=∠AEC=60°,DE=EC,
∵AE=AR,
∴△AER时等边三角形,
∴AE=ER,∠EAR=60°,
∵∠EAR=∠BAC=60°,
∴∠EAB=∠RAC,
∵AE=AR,AB=AC,
∴△AEB≌△ARC(SAS),
∴BE=CR=3,
设EF=x,则AE=ER=x+2,DE=EC=x+2+3=x+5,
∵∠DFE=90°,∠EDF=30°,
∴DE=2EF=2x,
∴2x=x+5,
∴x=5,
∴DE=2x=10.
27.已知,在平面直角坐标系中,点O为坐标原点,A点坐标为(0,a),B点坐标为(b,0),且满足a2﹣12a+36+=0.
(1)如图1,求OA、OB的长;
(2)如图2,P是y轴负半轴上一点,点C在第二象限,连接AC、BC、PC、PB,且PB=PC,∠BPC=90°,设OP=t,请用含t的式子表示△APC的面积;
(3)如图3,在(2)的条件下,作AD∥x轴交BC的延长线于点D,BD与y轴交于点E,若E是BD的中点,求t值.
【分析】(1)利用非负数的性质求出a,b的值可得结论;
(2)如图2中,过点C作CH⊥AP于点H.证明△PHC≌△BOP(AAS),推出CH=OP=t,可得结论;
(3)证明△ADE≌△OBE(ASA),推出AD=OB=6,AE=EO=3,由△PHC≌△BOP,推出PH=OB=OA=6,推出AH=OP=t,EH=3﹣t,由CH∥AD,推出=,可得=,解方程即可解决问题.
解:(1)∵a2﹣12a+36+=0,
∴(a﹣6)2+=0,
又∵(a﹣6)2≥0,≥0,
∴a=b=6,
∴A(0,6),B(6,0),
∴OA=OB=6;
(2)如图2中,过点C作CH⊥AP于点H.
∵∠BPC=∠CHP=∠BOP=90°,
∴∠CPH+∠BPO=90°,∠BPO+∠OBP=90°,
∴∠CPH=∠PBO,
∵PC=PB,
∴△PHC≌△BOP(AAS),
∴CH=OP=t,
∵AP=PO+OA=t+6,
∴S△ACP= AP CH=×(t+6)×t=t2+3t(t<0);
(3)如图3在,过点C作CH⊥OA于点H.
∵AD∥OB,
∴∠D=∠OBE,
∵∠AED=∠BEO,DE=EB,
∴△ADE≌△OBE(ASA),
∴AD=OB=6,AE=EO=3,
∵△PHC≌△BOP,
∴PH=OB=OA=6,
∴AH=OP=t,
∴EH=3﹣t,
∵CH∥AD,
∴=,
∴=,
解得t=2.
同课章节目录
