2021-2022学年苏科版七年级数学下册7.4认识三角形课前预习练 (word版含解析)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.4认识三角形课前预习练 (word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 407.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览


文档简介
7.4认识三角形【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、小明作△ABC中AC边上的高线,下列三角板的摆放位置正确的是( )
A.B. C.D.
2、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
4、若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
5、袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
6、下列说法正确的是( )
①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;④三角形的三条高都在三角形内部.
A.①② B.②③ C.③④ D.②④
7、如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
(7题) (8题) (9题)
8、如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
9、已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c B.2a+2b C.2c D.0
10、如图,在△ABC中,D、E分别是BC、AD的中点,点F在BE上,且EF=2BF,若S△BCF=2cm2,则S△ABC为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
二、填空题
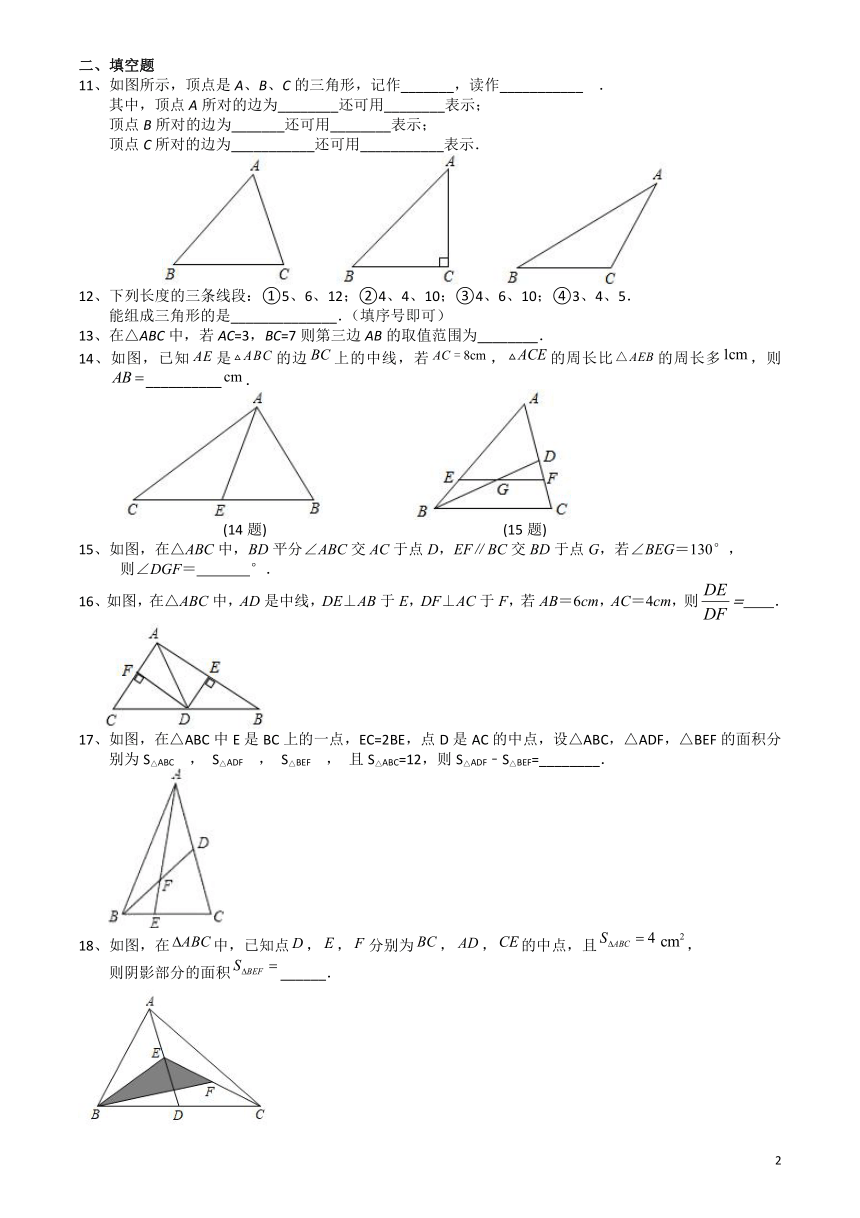
11、如图所示,顶点是A、B、C的三角形,记作_______,读作___________ .
其中,顶点A所对的边为________还可用________表示;
顶点B所对的边为_______还可用________表示;
顶点C所对的边为___________还可用___________表示.
12、下列长度的三条线段:①5、6、12;②4、4、10;③4、6、10;④3、4、5.
能组成三角形的是______________.(填序号即可)
13、在△ABC中,若AC=3,BC=7则第三边AB的取值范围为________.
14、如图,已知是的边上的中线,若,的周长比的周长多,则__________.
(14题) (15题)
15、如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,
则∠DGF= °.
16、如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则= .
17、如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=________.
18、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
三、解答题
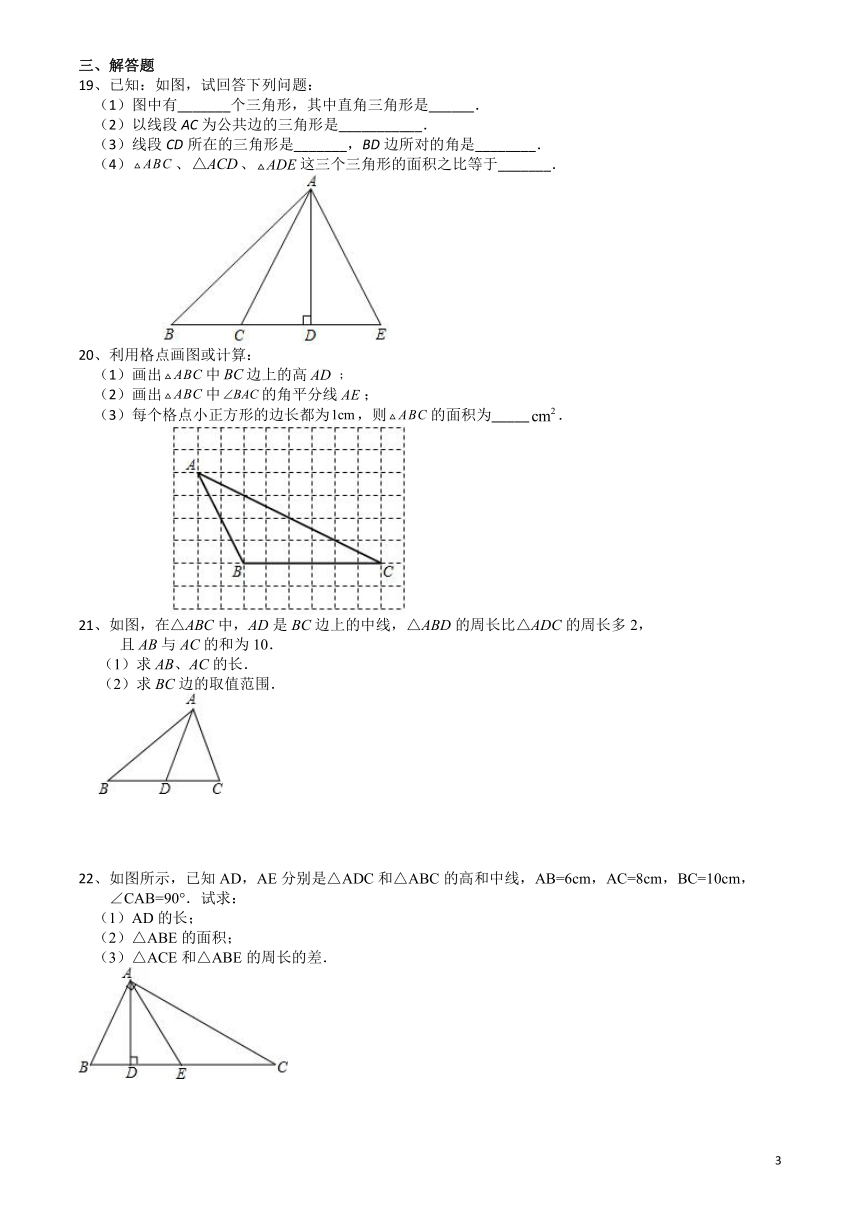
19、已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)、、这三个三角形的面积之比等于_______.
20、利用格点画图或计算:
(1)画出中边上的高﹔
(2)画出中的角平分线;
(3)每个格点小正方形的边长都为,则的面积为_____.
21、如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,
且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
22、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
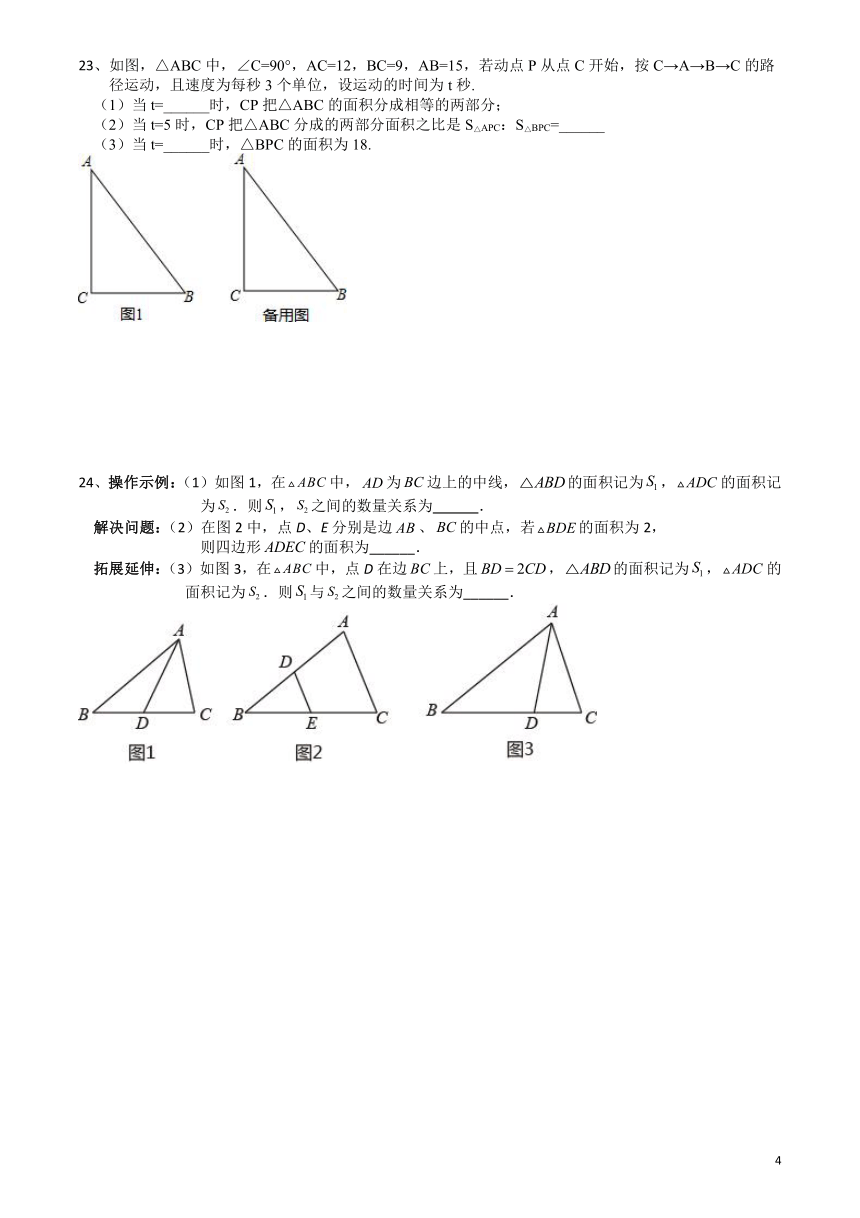
23、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
24、操作示例:(1)如图1,在中,为边上的中线,的面积记为,的面积记为.则,之间的数量关系为 .
解决问题:(2)在图2中,点D、E分别是边、的中点,若的面积为2,
则四边形的面积为______.
拓展延伸:(3)如图3,在中,点D在边上,且,的面积记为,的面积记为.则与之间的数量关系为______.
7.4认识三角形【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、小明作△ABC中AC边上的高线,下列三角板的摆放位置正确的是( )
A.B. C.D.
【分析】根据三角形高的定义进行判断.
【解答】解:作△ABC中AC边上的高线,即过B点作AC的垂线,垂线段为AC边上的高.
故选:D.
2、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
【答案】C
【解析】解:AC边上的高就是过B作垂线垂直AC交AC于某点,因此只有选项C符合条件;
故选C.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
【答案】A
【解析】
解:根据三角形的高的定义,AD为△ABC中BC边上的高.
故选:A.
4、若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
【分析】首先设第三边长为xcm,根据三角形的三边关系可得6﹣3<x<6+3,再解不等式即可.
【解析】设第三边长为xcm,根据三角形的三边关系可得:
6﹣3<x<6+3,
解得:3<x<9,
故选:C.
5、袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
【分析】先设第三根木棒的长为xcm,再根据三角形的三边关系求出x的取值范围,找出不符合条件的x的值即可.
【解析】设第三根木棒的长为xcm,
∵已经取了10cm和15cm两根木棍,
∴15﹣10<x<15+10,即5<x<25.
∴四个选项中只有D不在其范围内,符合题意.
故选:D.
6、下列说法正确的是( )
①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;④三角形的三条高都在三角形内部.
A.①② B.②③ C.③④ D.②④
【答案】B
【解析】
解:①三角形的角平分线是线段,故①说法错误;
②三角形的三条角平分线都在三角形内部,故②说法正确;
③因为三角形的一条中线把该三角形分成的两个三角形等底同高,所以这两部分的面积相等,故③说法正确;
④锐角三角形的三条高都在三角形内部;直角三角形有两条高与直角边重合,另一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部.故④说法错误.
故正确的有②③.
故选:B.
7、如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
【答案】C
【解析】
解:AD是三角形ABC的角平分线,
则是∠BAC的角平分线,
所以AO是△ABE的角平分线,故①正确;
BE是三角形ABC的中线,
则E是AC是中点,而O不一定是AD的中点,故②错误.
故选:C.
8、如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
【分析】根据三角形的角平分线、中线和高的概念判断.
【解析】∵AF是△ABC的中线,
∴BF=CF,A说法正确,不符合题意;
∵AD是高,
∴∠ADC=90°,
∴∠C+∠CAD=90°,B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF,D说法正确,不符合题意;
故选:C.
9、已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c B.2a+2b C.2c D.0
【分析】根据三角形的三边关系“两边之和>第三边,两边之差<第三边”,判断式子的符号,再根据绝对值的意义去掉绝对值即可.
【解答】解:根据三角形的三边关系,两边之和大于第三边,
得a+b﹣c>0,c﹣a﹣b<0,
故|a+b﹣c|﹣|c﹣a﹣b|=a+b﹣c+c﹣a﹣b=0.
故选:D.
10、如图,在△ABC中,D、E分别是BC、AD的中点,点F在BE上,且EF=2BF,若S△BCF=2cm2,则S△ABC为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
【分析】根据EF=2BF,S△BCF=2cm2,求得S△BEC=3S△BCF=6cm2,根据三角形中线把三角形分成两个面积相等的三角形可得S△BDE=S△CDE=S△BEC=3cm2,从而求出S△ABD=S△ACD=2S△BDE=6cm2,再根据S△ABC=2S△ABD计算即可得解.
【解析】如图,∵EF=2BF,若S△BCF=2cm2,
∴S△BEC=3S△BCF=3×2=6cm2,
∵D是BD的中点,
∴S△BDE=S△CDE=S△BEC=3cm2,
∵E是AD的中点,
∴S△ABD=S△ACD=2S△BDE=6cm2,
∴△ABC的面积为12cm2,
故选:C.
二、填空题
11、如图所示,顶点是A、B、C的三角形,记作_______,读作___________ .
其中,顶点A所对的边为________还可用________表示;
顶点B所对的边为_______还可用________表示;
顶点C所对的边为___________还可用___________表示.
【答案】 三角形ABC BC a AC b AB c
【解析】
解:如图所示,顶点是A、B、C的三角形,记作△ABC,读作三角形ABC.其中,顶点A所对的边为BC还可用a表示;顶点B所对的边为AC还可用b表示;顶点C所对的边为AB还可用c表示.
故答案为:△ABC;三角形ABC;BC;a;AC;b;AB;c.
12、下列长度的三条线段:①5、6、12;②4、4、10;③4、6、10;④3、4、5.
能组成三角形的是______________.(填序号即可)
【答案】④
【解析】解:①5+6<12,不能组成三角形;
②4+4<10,不能组成三角形;
③4+6=10,不能组成三角形;
④3+4>5,能组成三角形.
故答案为:④.
13、在△ABC中,若AC=3,BC=7则第三边AB的取值范围为________.
【答案】4<AB<10
【解析】
解:∵在△ABC中,AC=3,BC=7,
,
即,
解得.
故答案为:.
14、如图,已知是的边上的中线,若,的周长比的周长多,则__________.
【答案】7
【解析】
解:是的边上的中线,
,
的周长比的周长多,且,
,即,
解得,
故答案为:7.
15、如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,
则∠DGF= °.
【分析】根据角平分线的定义得到∠EBG=∠CBG,根据平行线的性质得到∠EGB=∠CBG,等量代换得到∠EBG=∠EGB,再根据三角形的内角和定理和对顶角的性质于是得到结论.
【解答】解:∵EF∥BC,
∴∠EGB=∠CBG,
∵BD平分∠ABC,
∴∠EBG=∠CBG,
∴∠EBG=∠EGB,
∵∠BEG=130°,
∴∠EGB==25°,
∴∠DGF=∠EGB=25°.
故答案为:25.
16、如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则= .
【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.
【解答】解:∵△ABC中,AD为中线,
∴BD=DC.
∴S△ABD=S△ADC.
∵DE⊥AB于E,DF⊥AC于F,AB=6,AC=4.
∴ AB ED= AC DF,
∴×6×ED=×4×DF,
∴.
故答案为:.
17、如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=________.
【答案】2
【分析】S△ADF﹣S△BEF=S△ABD﹣S△ABE , 所以求出三角形ABD的面积和三角形ABE的面积即可,因为EC=2BE,点D是AC的中点,且S△ABC=12,就可以求出三角形ABD的面积和三角形ABE的面积.
【解析】【解答】解:∵点D是AC的中点,
∴AD= AC,
∵S△ABC=12,
∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE= S△ABC= ×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF ,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:2.
18、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
【答案】
【解析】
解:∵AD为△ABC中线
∴S△ABD=S△ACD,
又∵E为AD中点,
故,
∴,
∵BF为△BEC中线,
∴cm2.
故答案为:1cm2.
三、解答题
19、已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)、、这三个三角形的面积之比等于_______.
【答案】6 ,, ,,
BC:CD:DE
【解析】
(1)由图可知,
图中三角形有△ABC、△ADB、△AEB、△ACD、△ACE、△ADE,
图中有6个三角形,
由图可知,直角三角形有,,;
(2)由图可知,
以线段AC为公共边的三角形是,,;
(3)由图可知,
线段CD所在的三角形是,
BD边所对的角是;
(4)
故答案为:6;,,;,,;;;BC:CD:DE.
20、利用格点画图或计算:
(1)画出中边上的高﹔
(2)画出中的角平分线;
(3)每个格点小正方形的边长都为,则的面积为_____.
【答案】(1)见解析;(2)见解析;(3)12
【解析】解:(1)画出CB边上的高AD,如图所示;
(2)画出△ABC中∠BAC的角平分线AE,如图所示;
(3)由网格得:AD=4cm,BC=6cm,
则S△ABC=BC AD=×6×4=12cm2.
故答案为:12.
21、如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,
且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
【分析】(1)根据三角形中线的定义,BD=CD.所以△ABD和△ADC的周长之差也就是AB与AC的差,然后联立关于AB、AC的二元一次方程组,利用加减消元法求解即可.
(2)根据三角形三边关系解答即可.
【解答】解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
22、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
【答案】⑴4.8cm;⑵12cm ;⑶2cm.
【分析】
(1)利用直角三角形面积的两种求法求线段AD的长度即可;(2)先求△ABC的面积,再根据△AEC与△ABE是等底同高的两个三角形,它们的面积相等,由此即可求得△ABE的面;(3)由AE是中线,可得BE=CE,根据△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,即可求解.
【详解】
∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD= =4.8(cm),
即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm.
23、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
【答案】(1)6.5;(2)1:4;(3)或.
【分析】
(1)根据中线的性质可知,点P在AB中点,CP把△ABC的面积分成相等的两部分,进而求解即可;
(2)求出当时,与的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①当P在AC上时;②当P在AB上时.
【详解】
(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时
∵点P在AB中点∴
∴CA+AP=12+7.5=19.5(cm),∴3t=19.5,解得t=6.5.
故当t=6.5时,CP把△ABC的面积分成相等的两部分;
(2)5×3=15,AP=15-12=3,BP=15-3=12,则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=18,∴×9×CP=18,∴CP=4,∴3t=4,∴t=;
②当P在AB上时,
∵△BCP的面积=18,△ABC面积=,
∴,∴3t=12+15×=22,解得t=.
故t=或秒时,△BCP的面积为18.
故答案为: 或.
24、操作示例:(1)如图1,在中,为边上的中线,的面积记为,的面积记为.则,之间的数量关系为 .
解决问题:(2)在图2中,点D、E分别是边、的中点,若的面积为2,
则四边形的面积为______.
拓展延伸:(3)如图3,在中,点D在边上,且,的面积记为,的面积记为.则与之间的数量关系为______.
【答案】(1);(2)6;(3).
【解析】解:(1)如图,过点作于点,
,
为边上的中线,,,
故答案为:;
(2)如图,连接,
由(1)得:,
,
则四边形的面积为,
故答案为:6;
(3)如图,取的中点,连接,则,
,
,即,,
,,即,
故答案为:.
(
1
)
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、小明作△ABC中AC边上的高线,下列三角板的摆放位置正确的是( )
A.B. C.D.
2、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
4、若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
5、袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
6、下列说法正确的是( )
①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;④三角形的三条高都在三角形内部.
A.①② B.②③ C.③④ D.②④
7、如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
(7题) (8题) (9题)
8、如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
9、已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c B.2a+2b C.2c D.0
10、如图,在△ABC中,D、E分别是BC、AD的中点,点F在BE上,且EF=2BF,若S△BCF=2cm2,则S△ABC为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
二、填空题
11、如图所示,顶点是A、B、C的三角形,记作_______,读作___________ .
其中,顶点A所对的边为________还可用________表示;
顶点B所对的边为_______还可用________表示;
顶点C所对的边为___________还可用___________表示.
12、下列长度的三条线段:①5、6、12;②4、4、10;③4、6、10;④3、4、5.
能组成三角形的是______________.(填序号即可)
13、在△ABC中,若AC=3,BC=7则第三边AB的取值范围为________.
14、如图,已知是的边上的中线,若,的周长比的周长多,则__________.
(14题) (15题)
15、如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,
则∠DGF= °.
16、如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则= .
17、如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=________.
18、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
三、解答题
19、已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)、、这三个三角形的面积之比等于_______.
20、利用格点画图或计算:
(1)画出中边上的高﹔
(2)画出中的角平分线;
(3)每个格点小正方形的边长都为,则的面积为_____.
21、如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,
且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
22、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
23、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
24、操作示例:(1)如图1,在中,为边上的中线,的面积记为,的面积记为.则,之间的数量关系为 .
解决问题:(2)在图2中,点D、E分别是边、的中点,若的面积为2,
则四边形的面积为______.
拓展延伸:(3)如图3,在中,点D在边上,且,的面积记为,的面积记为.则与之间的数量关系为______.
7.4认识三角形【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、小明作△ABC中AC边上的高线,下列三角板的摆放位置正确的是( )
A.B. C.D.
【分析】根据三角形高的定义进行判断.
【解答】解:作△ABC中AC边上的高线,即过B点作AC的垂线,垂线段为AC边上的高.
故选:D.
2、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
【答案】C
【解析】解:AC边上的高就是过B作垂线垂直AC交AC于某点,因此只有选项C符合条件;
故选C.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
【答案】A
【解析】
解:根据三角形的高的定义,AD为△ABC中BC边上的高.
故选:A.
4、若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是( )
A.2cm B.3cm C.6cm D.9cm
【分析】首先设第三边长为xcm,根据三角形的三边关系可得6﹣3<x<6+3,再解不等式即可.
【解析】设第三边长为xcm,根据三角形的三边关系可得:
6﹣3<x<6+3,
解得:3<x<9,
故选:C.
5、袁老师在课堂上组织学生用小棍摆三角形,小棍的长度有10cm,15cm,20cm和25cm四种规格,小朦同学已经取了10cm和15cm两根木棍,那么第三根木棍不可能取( )
A.10cm B.15cm C.20cm D.25cm
【分析】先设第三根木棒的长为xcm,再根据三角形的三边关系求出x的取值范围,找出不符合条件的x的值即可.
【解析】设第三根木棒的长为xcm,
∵已经取了10cm和15cm两根木棍,
∴15﹣10<x<15+10,即5<x<25.
∴四个选项中只有D不在其范围内,符合题意.
故选:D.
6、下列说法正确的是( )
①三角形的角平分线是射线;②三角形的三条角平分线都在三角形内部;
③三角形的一条中线把该三角形分成面积相等的两部分;④三角形的三条高都在三角形内部.
A.①② B.②③ C.③④ D.②④
【答案】B
【解析】
解:①三角形的角平分线是线段,故①说法错误;
②三角形的三条角平分线都在三角形内部,故②说法正确;
③因为三角形的一条中线把该三角形分成的两个三角形等底同高,所以这两部分的面积相等,故③说法正确;
④锐角三角形的三条高都在三角形内部;直角三角形有两条高与直角边重合,另一条高在三角形内部;钝角三角形有两条高在三角形外部,一条高在三角形内部.故④说法错误.
故正确的有②③.
故选:B.
7、如图,△ABC的角平分线AD,中线BE交于点O,则结论:①AO是△ABE的角平分线;②BO是△ABD的中线.其中( )
A.①、②都正确 B.①、②都不正确
C.①正确②不正确 D.①不正确,②正确
【答案】C
【解析】
解:AD是三角形ABC的角平分线,
则是∠BAC的角平分线,
所以AO是△ABE的角平分线,故①正确;
BE是三角形ABC的中线,
则E是AC是中点,而O不一定是AD的中点,故②错误.
故选:C.
8、如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是( )
A.BF=CF B.∠C+∠CAD=90°
C.∠BAF=∠CAF D.S△ABC=2S△ABF
【分析】根据三角形的角平分线、中线和高的概念判断.
【解析】∵AF是△ABC的中线,
∴BF=CF,A说法正确,不符合题意;
∵AD是高,
∴∠ADC=90°,
∴∠C+∠CAD=90°,B说法正确,不符合题意;
∵AE是角平分线,
∴∠BAE=∠CAE,C说法错误,符合题意;
∵BF=CF,
∴S△ABC=2S△ABF,D说法正确,不符合题意;
故选:C.
9、已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c B.2a+2b C.2c D.0
【分析】根据三角形的三边关系“两边之和>第三边,两边之差<第三边”,判断式子的符号,再根据绝对值的意义去掉绝对值即可.
【解答】解:根据三角形的三边关系,两边之和大于第三边,
得a+b﹣c>0,c﹣a﹣b<0,
故|a+b﹣c|﹣|c﹣a﹣b|=a+b﹣c+c﹣a﹣b=0.
故选:D.
10、如图,在△ABC中,D、E分别是BC、AD的中点,点F在BE上,且EF=2BF,若S△BCF=2cm2,则S△ABC为( )
A.4cm2 B.8cm2 C.12cm2 D.16cm2
【分析】根据EF=2BF,S△BCF=2cm2,求得S△BEC=3S△BCF=6cm2,根据三角形中线把三角形分成两个面积相等的三角形可得S△BDE=S△CDE=S△BEC=3cm2,从而求出S△ABD=S△ACD=2S△BDE=6cm2,再根据S△ABC=2S△ABD计算即可得解.
【解析】如图,∵EF=2BF,若S△BCF=2cm2,
∴S△BEC=3S△BCF=3×2=6cm2,
∵D是BD的中点,
∴S△BDE=S△CDE=S△BEC=3cm2,
∵E是AD的中点,
∴S△ABD=S△ACD=2S△BDE=6cm2,
∴△ABC的面积为12cm2,
故选:C.
二、填空题
11、如图所示,顶点是A、B、C的三角形,记作_______,读作___________ .
其中,顶点A所对的边为________还可用________表示;
顶点B所对的边为_______还可用________表示;
顶点C所对的边为___________还可用___________表示.
【答案】 三角形ABC BC a AC b AB c
【解析】
解:如图所示,顶点是A、B、C的三角形,记作△ABC,读作三角形ABC.其中,顶点A所对的边为BC还可用a表示;顶点B所对的边为AC还可用b表示;顶点C所对的边为AB还可用c表示.
故答案为:△ABC;三角形ABC;BC;a;AC;b;AB;c.
12、下列长度的三条线段:①5、6、12;②4、4、10;③4、6、10;④3、4、5.
能组成三角形的是______________.(填序号即可)
【答案】④
【解析】解:①5+6<12,不能组成三角形;
②4+4<10,不能组成三角形;
③4+6=10,不能组成三角形;
④3+4>5,能组成三角形.
故答案为:④.
13、在△ABC中,若AC=3,BC=7则第三边AB的取值范围为________.
【答案】4<AB<10
【解析】
解:∵在△ABC中,AC=3,BC=7,
,
即,
解得.
故答案为:.
14、如图,已知是的边上的中线,若,的周长比的周长多,则__________.
【答案】7
【解析】
解:是的边上的中线,
,
的周长比的周长多,且,
,即,
解得,
故答案为:7.
15、如图,在△ABC中,BD平分∠ABC交AC于点D,EF∥BC交BD于点G,若∠BEG=130°,
则∠DGF= °.
【分析】根据角平分线的定义得到∠EBG=∠CBG,根据平行线的性质得到∠EGB=∠CBG,等量代换得到∠EBG=∠EGB,再根据三角形的内角和定理和对顶角的性质于是得到结论.
【解答】解:∵EF∥BC,
∴∠EGB=∠CBG,
∵BD平分∠ABC,
∴∠EBG=∠CBG,
∴∠EBG=∠EGB,
∵∠BEG=130°,
∴∠EGB==25°,
∴∠DGF=∠EGB=25°.
故答案为:25.
16、如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=4cm,则= .
【分析】由题意,△ABC中,AD为中线,可知△ABD和△ADC的面积相等;利用面积相等,问题可求.
【解答】解:∵△ABC中,AD为中线,
∴BD=DC.
∴S△ABD=S△ADC.
∵DE⊥AB于E,DF⊥AC于F,AB=6,AC=4.
∴ AB ED= AC DF,
∴×6×ED=×4×DF,
∴.
故答案为:.
17、如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=________.
【答案】2
【分析】S△ADF﹣S△BEF=S△ABD﹣S△ABE , 所以求出三角形ABD的面积和三角形ABE的面积即可,因为EC=2BE,点D是AC的中点,且S△ABC=12,就可以求出三角形ABD的面积和三角形ABE的面积.
【解析】【解答】解:∵点D是AC的中点,
∴AD= AC,
∵S△ABC=12,
∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,
∴S△ABE= S△ABC= ×12=4,
∵S△ABD﹣S△ABE=(S△ADF+S△ABF)﹣(S△ABF+S△BEF)=S△ADF﹣S△BEF ,
即S△ADF﹣S△BEF=S△ABD﹣S△ABE=6﹣4=2.
故答案为:2.
18、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
【答案】
【解析】
解:∵AD为△ABC中线
∴S△ABD=S△ACD,
又∵E为AD中点,
故,
∴,
∵BF为△BEC中线,
∴cm2.
故答案为:1cm2.
三、解答题
19、已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)、、这三个三角形的面积之比等于_______.
【答案】6 ,, ,,
BC:CD:DE
【解析】
(1)由图可知,
图中三角形有△ABC、△ADB、△AEB、△ACD、△ACE、△ADE,
图中有6个三角形,
由图可知,直角三角形有,,;
(2)由图可知,
以线段AC为公共边的三角形是,,;
(3)由图可知,
线段CD所在的三角形是,
BD边所对的角是;
(4)
故答案为:6;,,;,,;;;BC:CD:DE.
20、利用格点画图或计算:
(1)画出中边上的高﹔
(2)画出中的角平分线;
(3)每个格点小正方形的边长都为,则的面积为_____.
【答案】(1)见解析;(2)见解析;(3)12
【解析】解:(1)画出CB边上的高AD,如图所示;
(2)画出△ABC中∠BAC的角平分线AE,如图所示;
(3)由网格得:AD=4cm,BC=6cm,
则S△ABC=BC AD=×6×4=12cm2.
故答案为:12.
21、如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,
且AB与AC的和为10.
(1)求AB、AC的长.
(2)求BC边的取值范围.
【分析】(1)根据三角形中线的定义,BD=CD.所以△ABD和△ADC的周长之差也就是AB与AC的差,然后联立关于AB、AC的二元一次方程组,利用加减消元法求解即可.
(2)根据三角形三边关系解答即可.
【解答】解:(1)∵AD是BC边上的中线,
∴BD=CD,
∴△ABD的周长﹣△ADC的周长=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC=2,
即AB﹣AC=2①,
又AB+AC=10②,
①+②得.2AB=12,
解得AB=6,
②﹣①得,2AC=8,
解得AC=4,
∴AB和AC的长分别为:AB=6,AC=4;
(2)∵AB=6,AC=4,
∴2<BC<10.
22、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
【答案】⑴4.8cm;⑵12cm ;⑶2cm.
【分析】
(1)利用直角三角形面积的两种求法求线段AD的长度即可;(2)先求△ABC的面积,再根据△AEC与△ABE是等底同高的两个三角形,它们的面积相等,由此即可求得△ABE的面;(3)由AE是中线,可得BE=CE,根据△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE),化简可得△ACE的周长-△ABE的周长=AC-AB,即可求解.
【详解】
∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD= =4.8(cm),
即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm.
23、如图,△ABC中,∠C=90°,AC=12,BC=9,AB=15,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3个单位,设运动的时间为t秒.
(1)当t=______时,CP把△ABC的面积分成相等的两部分;
(2)当t=5时,CP把△ABC分成的两部分面积之比是S△APC:S△BPC=______
(3)当t=______时,△BPC的面积为18.
【答案】(1)6.5;(2)1:4;(3)或.
【分析】
(1)根据中线的性质可知,点P在AB中点,CP把△ABC的面积分成相等的两部分,进而求解即可;
(2)求出当时,与的长,再根据等高的三角形面积比等于底边的比求解即可;
(3)分两种情况:①当P在AC上时;②当P在AB上时.
【详解】
(1)当点P在AB中点时,CP把△ABC的面积分成相等的两部分,此时
∵点P在AB中点∴
∴CA+AP=12+7.5=19.5(cm),∴3t=19.5,解得t=6.5.
故当t=6.5时,CP把△ABC的面积分成相等的两部分;
(2)5×3=15,AP=15-12=3,BP=15-3=12,则S△APC:S△BPC=3:12=1:4;
(3)分两种情况:
①当P在AC上时,
∵△BCP的面积=18,∴×9×CP=18,∴CP=4,∴3t=4,∴t=;
②当P在AB上时,
∵△BCP的面积=18,△ABC面积=,
∴,∴3t=12+15×=22,解得t=.
故t=或秒时,△BCP的面积为18.
故答案为: 或.
24、操作示例:(1)如图1,在中,为边上的中线,的面积记为,的面积记为.则,之间的数量关系为 .
解决问题:(2)在图2中,点D、E分别是边、的中点,若的面积为2,
则四边形的面积为______.
拓展延伸:(3)如图3,在中,点D在边上,且,的面积记为,的面积记为.则与之间的数量关系为______.
【答案】(1);(2)6;(3).
【解析】解:(1)如图,过点作于点,
,
为边上的中线,,,
故答案为:;
(2)如图,连接,
由(1)得:,
,
则四边形的面积为,
故答案为:6;
(3)如图,取的中点,连接,则,
,
,即,,
,,即,
故答案为:.
(
1
)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
