2021-2022学年苏科版七年级数学下册第7章 平面图形的认识(二) 测试题 (word版含解析)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册第7章 平面图形的认识(二) 测试题 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 728.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 12:48:43 | ||
图片预览


文档简介
7章:平面图形的认识(二) 章末整合提升(2)【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、如图所示,下列说法错误的是( )
A.∠1和∠3是同位角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠5和∠6是内错角
(1题) (3题) (4题)
2、下列各组图形中,一个图形经过平移能得到另一个图形的是( )
A. B. C. D.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
4、如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
5、如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
(5题) (6题) (7题)
6、如图,下列条件能判断直线l1//l2有( )
①;②;③;④;⑤
A. 1个 B. 2个 C. 3个 D. 4个
7、如图,把纸片沿折叠,当点落在四边形的外部时,此时测得,,则的度数为
A. B. C. D.
8、如图,若AB∥CD,CD∥EF,那么BCE=( )
A. 180°-2+1 B. 180°-1-2 C. 2=21 D. 1+2
(8题) (9题)
9、如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3=( )
A.70° B.180° C.110° D.80°
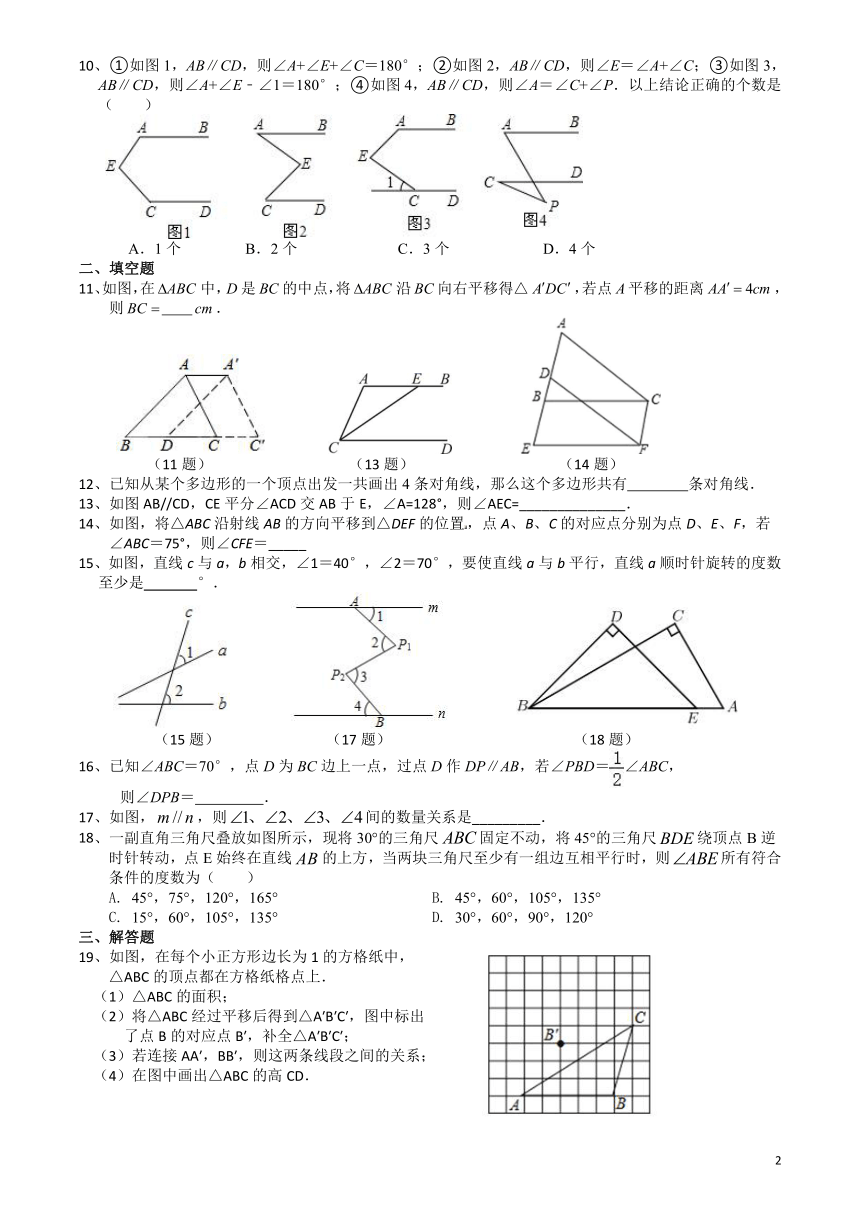
10、①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠E=∠A+∠C;③如图3,AB∥CD,则∠A+∠E﹣∠1=180°;④如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11、如图,在中,是的中点,将沿向右平移得△,若点平移的距离,则 .
(11题) (13题) (14题)
12、已知从某个多边形的一个顶点出发一共画出4条对角线,那么这个多边形共有 条对角线.
13、如图AB//CD,CE平分∠ACD交AB于E,∠A=128°,则∠AEC=______________.
14、如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=_____
15、如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
(15题) (17题) (18题)
16、已知∠ABC=70°,点D为BC边上一点,过点D作DP∥AB,若∠PBD=∠ABC,
则∠DPB= .
17、如图,,则间的数量关系是_________.
18、一副直角三角尺叠放如图所示,现将30°的三角尺固定不动,将45°的三角尺绕顶点B逆时针转动,点E始终在直线的上方,当两块三角尺至少有一组边互相平行时,则所有符合条件的度数为( )
A. 45°,75°,120°,165° B. 45°,60°,105°,135°
C. 15°,60°,105°,135° D. 30°,60°,90°,120°
三、解答题
19、如图,在每个小正方形边长为1的方格纸中,
△ABC的顶点都在方格纸格点上.
(1)△ABC的面积;
(2)将△ABC经过平移后得到△A′B′C′,图中标出
了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系;
(4)在图中画出△ABC的高CD.
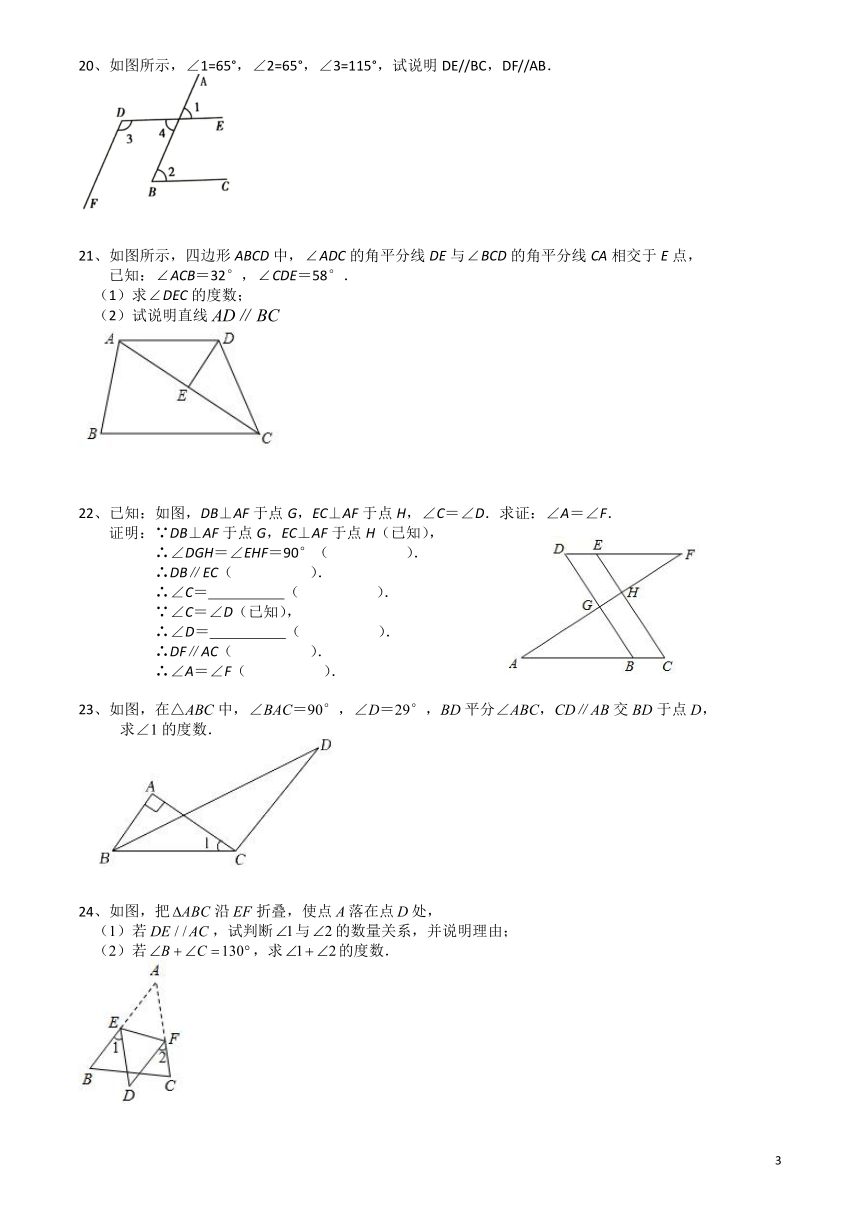
20、如图所示,∠1=65°,∠2=65°,∠3=115°,试说明DE//BC,DF//AB.
21、如图所示,四边形ABCD中,ADC的角平分线DE与BCD的角平分线CA相交于E点,
已知:ACB=32°,CDE=58°.
(1)求DEC的度数;
(2)试说明直线
22、已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
23、如图,在△ABC中,∠BAC=90°,∠D=29°,BD平分∠ABC,CD∥AB交BD于点D,
求∠1的度数.
24、如图,把沿折叠,使点落在点处,
(1)若,试判断与的数量关系,并说明理由;
(2)若,求的度数.
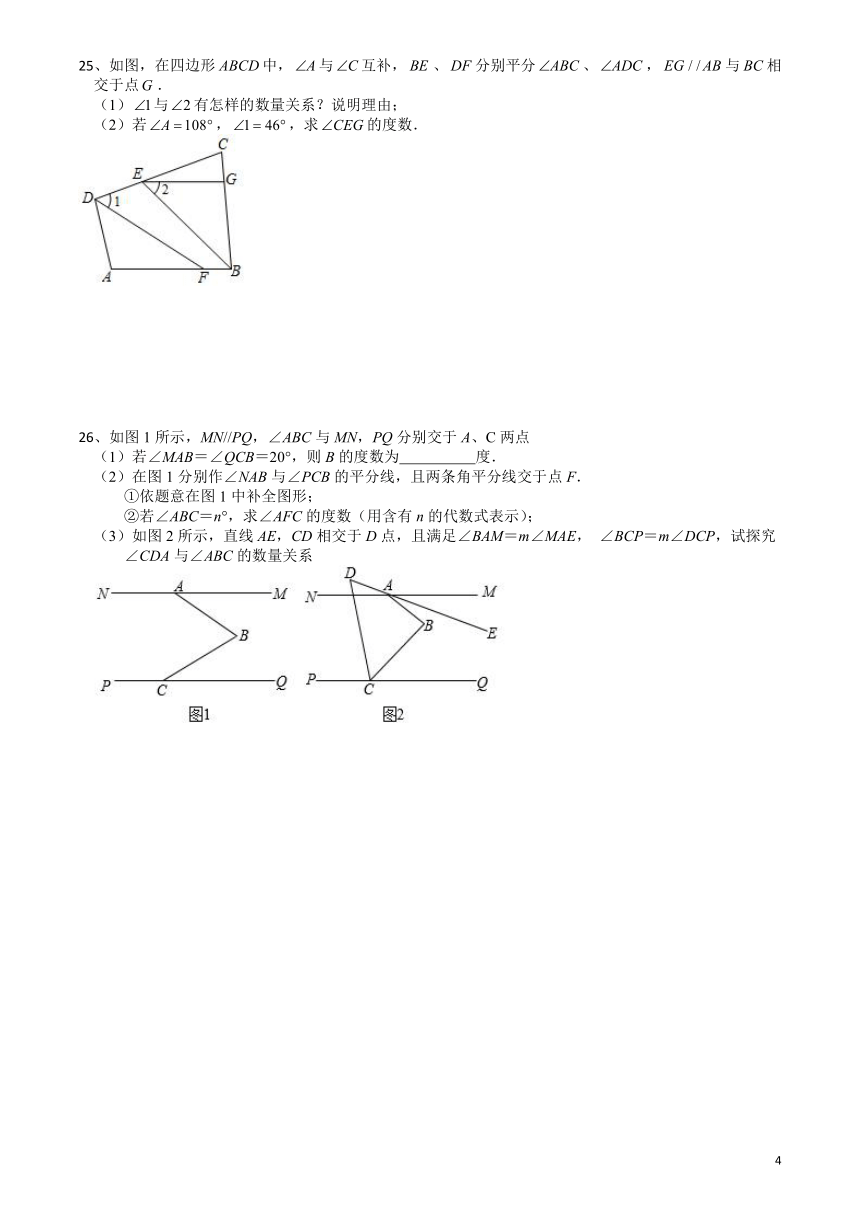
25、如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
26、如图1所示,MN//PQ,∠ABC与MN,PQ分别交于A、C两点
(1)若∠MAB=∠QCB=20°,则B的度数为 度.
(2)在图1分别作∠NAB与∠PCB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②若∠ABC=n°,求∠AFC的度数(用含有n的代数式表示);
(3)如图2所示,直线AE,CD相交于D点,且满足∠BAM=m∠MAE, ∠BCP=m∠DCP,试探究∠CDA与∠ABC的数量关系
7章:平面图形的认识(二) 章末整合提升(2)【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、如图所示,下列说法错误的是( )
A.∠1和∠3是同位角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠5和∠6是内错角
【答案】B
【解析】
解:A、∠1和∠3是同位角,故此选项不符合题意;
B、∠1和∠5不存在直接联系,故此选项符合题意;
C、∠1和∠2是同旁内角,故此选项不符合题意;
D、∠1和∠6是内错角,故此选项不符合题意;
故选B.
2、下列各组图形中,一个图形经过平移能得到另一个图形的是( )
A. B. C. D.
【答案】D
【解析】
解:各组图形中,选项D中的图形是一个图形经过平移能得到另一个图形,
故选:D.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
【答案】A
【解析】
解:根据三角形的高的定义,AD为△ABC中BC边上的高.
故选:A.
4、如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
【答案】D
【解析】
根据内错角相等,两直线平行,
∵∠A=∠2,
∴AB∥CD,
故选:D.
5、如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
【答案】A
【分析】
根据平行线的判定条件:同位角相等,两直线平行,同旁内角互补,两直线平行,内错角相等,两直线平行,进行逐一判断即可.
【详解】
解:A选项:当∠1=∠A时,可知是DE和AC被AB所截得到的同位角,可得到DE∥AC,而不是AB∥DF,故符合题意;
B选项:当∠A=∠3时,可知是AB、DF被AC所截得到的同位角,可得AB∥DF,故不符合题意;
C选项:当∠1=∠4时,可知是AB、DF被DE所截得到的内错角,可得AB∥DF,故不符合题意;
D选项:当∠2+∠A=180°时,是一对同旁内角,可得AB∥DF;故不符合题意;
故选A.
6、如图,下列条件能判断直线l1//l2有( )
①;②;③;④;⑤
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
【分析】根据平行线的判定定理进行依次判断即可.
【详解】①∵∠1,∠3互为内错角,∠1=∠3,∴;
②∵∠2,∠4互为同旁内角,∠2+∠4=180° ,∴;
③∠4,∠5互为同位角,∠4=∠5,∴;
④∠2,∠3没有位置关系,故不能证明 ,
⑤,,
∴∠1=∠3,
∴,
故选D.
7、如图,把纸片沿折叠,当点落在四边形的外部时,此时测得,,则的度数为
A. B. C. D.
【分析】根据折叠性质得出,根据三角形外角性质得出,.
【解析】如图,设与交于点,
,,
,,
,
,.
故选:.
8、如图,若AB∥CD,CD∥EF,那么BCE=( )
A. 180°-2+1 B. 180°-1-2 C. 2=21 D. 1+2
【答案】A
【解析】
【分析】根据两直线平行,内错角相等,同旁内角互补,这两条性质解答.
【详解】∵AB∥CD,CD∥EF,
∴∠1=∠BCD,∠ECD+∠2=180°,
∴BCE=∠BCD+∠ECD=180°-2+1,
故选A.
9、如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3=( )
A.70° B.180° C.110° D.80°
【分析】法一:延长直线后根据平行线的性质解答即可;
法二:过∠2的顶点作直线b的平行线,由平行线的性质可求解.
【解答】解:法一:延长直线,如图:
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故选:C.
法二:如图,过∠2的顶点作直线c∥b,
得∠3=∠4,
∴∠2﹣∠3=∠2﹣∠4,
∵a∥b,b∥c,
∴a∥c,
∴∠2﹣∠4=180°﹣∠1=180°﹣70°=110°,
即∠2﹣∠3=110°,
故选:C.
10、①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠E=∠A+∠C;③如图3,AB∥CD,则∠A+∠E﹣∠1=180°;④如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】①过点E作直线EF∥AB,由平行线的性质即可得出结论;
②过点E作直线EF∥AB,由平行线的性质即可得出结论;
③过点E作直线EF∥AB,由平行线的性质可得出∠A+∠E﹣∠1=180°;
④先根据三角形外角的性质得出∠1=∠C+∠P,再根据两直线平行,内错角相等即可作出判断.
【解答】解:①过点E作直线EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,
∴∠A+∠1=180°,∠2+∠C=180°,∴∠A+∠B+∠E=360°,故本小题错误;
②过点E作直线EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,∴∠A=∠1,∠2=∠C,
∴∠AEC=∠A+∠C,即∠E=∠A+∠C,故本小题正确;
③过点E作直线EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC﹣∠1=180°,即∠A+∠E﹣∠1=180°,故本选项正确;
④∵∠1是△CEP的外角,∴∠1=∠C+∠P,
∵AB∥CD,∴∠A=∠1,即∠A=∠C﹣∠P,故本小题正确.
综上所述,正确的小题有②③④共3个.
故选:C.
二、填空题
11、如图,在中,是的中点,将沿向右平移得△,若点平移的距离,则 .
【分析】利用平移的性质得到,然后根据是的中点可得到的长.
【解析】沿向右平移得△,
,
是的中点,
.
故答案为8.
12、已知从某个多边形的一个顶点出发一共画出4条对角线,那么这个多边形共有 条对角线.
【分析】根据对角线的概念,知一个多边形从一个顶点出发有条对角线,求出的值,再根据多边形对角线的总数为,即可解答.
【解析】从某个多边形的一个顶点出发一共画出4条对角线,
,
,
那么这个多边形对角线的总条数为:.
故答案为:14.
13、如图AB//CD,CE平分∠ACD交AB于E,∠A=128°,则∠AEC=______________.
【分析】首先根据ABCD,得到∠ACD=52°,再由CE平分∠ACD,得到∠ACE=∠DCE=26°,最后由两直线平行内错角相等,得到∠AEC=26°.
解:∵ABCD,∴∠AEC=∠DCE,∠A+∠ACD=180°,∴∠ACD=180°﹣∠A=180°﹣128°=52°,
∵CE平分∠ACD,∴∠ACE=∠DCE==26°,∴∠AEC=∠DCE=26°;
故答案为:26°.
14、如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=_____
【答案】105°
【解析】
解:由平移可知∠DEF=∠ABC=75°,
∵BE∥CF,
∴∠EFC=180°﹣∠DEF=180﹣75=105°
故答案是:105°.
15、如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
【分析】根据同位角相等两直线平行,求出旋转后∠2的同位角的度数,然后用∠3减去∠1即可得到直线a顺时针旋转的度数.
【解析】如图.
∵∠3=∠2=70°时,a∥b,
∴要使直线a与b平行,直线a顺时针旋转的度数至少是70°﹣40°=30°.
故答案为:30.
16、已知∠ABC=70°,点D为BC边上一点,过点D作DP∥AB,若∠PBD=∠ABC,则∠DPB= .
【分析】此题有两种情况,根据∠PBD=∠ABC,∠ABC=70°,得到∠PBD=35°,根据平行线的性质和三角形的外角的性质即可得到结论.
【解答】解:如图,∵∠PBD=∠ABC,∠ABC=70°,
∴∠PBD=35°,
∵PD∥AB,
∴∠P1DC=∠BDP2=70°,
∴∠DP1B=35°,∠DP2B=75°,
∴∠DPB=35°或75°,
故答案为:35°或75°.
17、如图,,则间的数量关系是_________.
【分析】分别过点P1、P2作P1C∥m,P2D∥m,由平行线的性质可知,∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,所以∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
18、一副直角三角尺叠放如图所示,现将30°的三角尺固定不动,将45°的三角尺绕顶点B逆时针转动,点E始终在直线的上方,当两块三角尺至少有一组边互相平行时,则所有符合条件的度数为( )
A. 45°,75°,120°,165° B. 45°,60°,105°,135°
C. 15°,60°,105°,135° D. 30°,60°,90°,120°
【答案】A
【解析】
【分析】分DE∥AB,DE∥AC,BE∥AC,AC∥BD,分别画出图形,根据平行线性质和三角板的特点求解.
【详解】解:如图,
①DE∥AB,∴∠D+∠ABD=180°
∴∠ABD=90°∴∠ABE=45°;
②DE∥AC,
∵∠D=∠C=90°,∴B,C,D共线,
∴∠ABE=∠CBE+∠ABC=180°-45°+30°=165°;
③BE∥AC,∴∠C=∠CBE=90°,
∴∠ABE=∠ABC+∠CBE=120°;
④AC∥BD,
∴∠ABD=180°-∠A=120°,∴∠ABE=∠ABD-∠DBE=75°,
综上:∠ABE的度数为:45°或75°或120°或165°.
三、解答题
19、如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系;
(4)在图中画出△ABC的高CD.
【答案】 解:(1)S△ABC=×5×4=10;
(2)如图所示:
(3)平行且相等;
(4)如图所示:
20、如图所示,∠1=65°,∠2=65°,∠3=115°,试说明DE//BC,DF//AB.
【答案】见解析
【解析】
解:∵∠1=65°,∠2=65°,
∴∠1=∠2,
∴DE∥BC ,
∵∠1=∠4=65°,∠3=115°,
∴∠3+∠4=65°+115°=180°,
∴DF∥AB.
21、如图所示,四边形ABCD中,ADC的角平分线DE与BCD的角平分线CA相交于E点,
已知:ACB=32°,CDE=58°.
(1)求DEC的度数;
(2)试说明直线
【答案】(1)90°;(2)见解析
【解析】
【分析】(1)根据三角形内角和定理即可求解;
(2)首先求得∠ADC的度数和∠DCB的度数,根据同旁内角互补,两直线平行即可证得.
【详解】解:(1)∵AC是BCD的平分线
∴
∵
∴∠DEC=180°-∠ACD-∠CDE=180°-32°-58°=90°;
(2)∵DE平分∠ADC,CA平分∠BCD
∴∠ADC=2∠CDE=116°,∠BCD=2∠ACD=64°
∵∠ADC+∠BCD=116°+64°=180°
∴
22、已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
【答案】垂直的定义;同位角相等,两直线平行;∠DBA;两直线平行,同位角相等;∠DBA;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
【解析】
【分析】先证DB∥EC,得∠C=∠DBA,再证∠D=∠DBA,得DF∥AC,然后由平行线的性质即可得出结论.
【详解】解:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°(垂直的定义),
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠DBA(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠DBA,两直线平行,同位角相等;∠DBA,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
23、如图,在△ABC中,∠BAC=90°,∠D=29°,BD平分∠ABC,CD∥AB交BD于点D,
求∠1的度数.
【分析】由平行线的性质可得∠ABD=∠D=29°,再由角平分线的定义得∠ABC=58°,结合∠BAC=90°,即可求∠1的度数.
解:∵CD∥AB,∴∠ABD=∠D=29°,
∵BD平分∠ABDC,∴∠ABC=2∠ABD=58°,
∵∠BAC=90°,∴∠1与∠ABC互余,
∴∠1=90°﹣58°=32°.
故∠1的度数为32°.
24、如图,把沿折叠,使点落在点处,
(1)若,试判断与的数量关系,并说明理由;
(2)若,求的度数.
【分析】(1)根据折叠的性质得到,根据平行线的性质得到,,所等量代换得到.
(2)根据三角形的内角和定理得到,根据折叠的性质得到,,所根据四边形的内角和等于得到,于是得到结论.
【解析】(1),理由如下:
是由翻折得到,,
,,,.
(2),,,
是由翻折得到,,,
,
,.
25、如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
【分析】(1)根据四边形的内角和为以及补角的定义可得,再根据角平分线的定义以及平行线的性质即可得出;
(2)根据与互补可得的度数,根据与互余可得的度数,根据平行线的性质可得的度数,然后根据三角形的内角和以及角的和差关系计算即可.
【解析】(1)与互余.
四边形的内角和为,与互补,
,
、分别平分、,,,
,,
,即与互余.
(2)由(1)知,,
,,与互补,,,
,,
平分,,
,.
26、如图1所示,MN//PQ,∠ABC与MN,PQ分别交于A、C两点
(1)若∠MAB=∠QCB=20°,则B的度数为 度.
(2)在图1分别作∠NAB与∠PCB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②若∠ABC=n°,求∠AFC的度数(用含有n的代数式表示);
(3)如图2所示,直线AE,CD相交于D点,且满足∠BAM=m∠MAE, ∠BCP=m∠DCP,试探究∠CDA与∠ABC的数量关系
【答案】(1)40;(2)①见解析;②;(3)m∠CDA+∠ABC=180°
【解析】
【分析】(1)作MN、PQ的平行线HG,根据两直线平行,内错角相等即可解答;
(2)①根据题意作图即可,②过F作 ,根据两直线平行,同旁内角互补和内错角相等即可解答;
(3)延长AE交PQ于点G,设∠MAE=x°,∠DCP=y°,知∠BAM=m∠MAE=mx°,∠BCP=m∠DCP=my°,∠BCQ=180° my°,根据(1)中所得结论知∠ABC=mx°+180° my°,即y° x°= ,由MNPQ知∠MAE=∠DGP=x°,根据∠CDA=∠DCP ∠DGC可得答案.
【详解】解:(1)作 ,
∵MN//PQ,∴,
∴ ,∴ ;
(2)①如图所示,
②过点F作 ,
∴ ,
∴ ,
∵ ,
∴ ,
∵∴ ,
∴ ,
∵ ,∴ ;
(3)延长AE交PQ于点G,
设∠MAE=x°,∠DCP=y°,则∠BAM=m∠MAE=mx°,∠BCP=m∠DCP=my°,
∴∠BCQ=180° my°,
由(1)知,∠ABC=mx°+180° my°,
∴y° x°=,
∵MNPQ,∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP ∠DGC=y° x°=,
即m∠CDA+∠ABC=180°.
(
1
)
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、如图所示,下列说法错误的是( )
A.∠1和∠3是同位角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠5和∠6是内错角
(1题) (3题) (4题)
2、下列各组图形中,一个图形经过平移能得到另一个图形的是( )
A. B. C. D.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
4、如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
5、如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
(5题) (6题) (7题)
6、如图,下列条件能判断直线l1//l2有( )
①;②;③;④;⑤
A. 1个 B. 2个 C. 3个 D. 4个
7、如图,把纸片沿折叠,当点落在四边形的外部时,此时测得,,则的度数为
A. B. C. D.
8、如图,若AB∥CD,CD∥EF,那么BCE=( )
A. 180°-2+1 B. 180°-1-2 C. 2=21 D. 1+2
(8题) (9题)
9、如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3=( )
A.70° B.180° C.110° D.80°
10、①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠E=∠A+∠C;③如图3,AB∥CD,则∠A+∠E﹣∠1=180°;④如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11、如图,在中,是的中点,将沿向右平移得△,若点平移的距离,则 .
(11题) (13题) (14题)
12、已知从某个多边形的一个顶点出发一共画出4条对角线,那么这个多边形共有 条对角线.
13、如图AB//CD,CE平分∠ACD交AB于E,∠A=128°,则∠AEC=______________.
14、如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=_____
15、如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
(15题) (17题) (18题)
16、已知∠ABC=70°,点D为BC边上一点,过点D作DP∥AB,若∠PBD=∠ABC,
则∠DPB= .
17、如图,,则间的数量关系是_________.
18、一副直角三角尺叠放如图所示,现将30°的三角尺固定不动,将45°的三角尺绕顶点B逆时针转动,点E始终在直线的上方,当两块三角尺至少有一组边互相平行时,则所有符合条件的度数为( )
A. 45°,75°,120°,165° B. 45°,60°,105°,135°
C. 15°,60°,105°,135° D. 30°,60°,90°,120°
三、解答题
19、如图,在每个小正方形边长为1的方格纸中,
△ABC的顶点都在方格纸格点上.
(1)△ABC的面积;
(2)将△ABC经过平移后得到△A′B′C′,图中标出
了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系;
(4)在图中画出△ABC的高CD.
20、如图所示,∠1=65°,∠2=65°,∠3=115°,试说明DE//BC,DF//AB.
21、如图所示,四边形ABCD中,ADC的角平分线DE与BCD的角平分线CA相交于E点,
已知:ACB=32°,CDE=58°.
(1)求DEC的度数;
(2)试说明直线
22、已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
23、如图,在△ABC中,∠BAC=90°,∠D=29°,BD平分∠ABC,CD∥AB交BD于点D,
求∠1的度数.
24、如图,把沿折叠,使点落在点处,
(1)若,试判断与的数量关系,并说明理由;
(2)若,求的度数.
25、如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
26、如图1所示,MN//PQ,∠ABC与MN,PQ分别交于A、C两点
(1)若∠MAB=∠QCB=20°,则B的度数为 度.
(2)在图1分别作∠NAB与∠PCB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②若∠ABC=n°,求∠AFC的度数(用含有n的代数式表示);
(3)如图2所示,直线AE,CD相交于D点,且满足∠BAM=m∠MAE, ∠BCP=m∠DCP,试探究∠CDA与∠ABC的数量关系
7章:平面图形的认识(二) 章末整合提升(2)【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、如图所示,下列说法错误的是( )
A.∠1和∠3是同位角 B.∠1和∠5是同位角
C.∠1和∠2是同旁内角 D.∠5和∠6是内错角
【答案】B
【解析】
解:A、∠1和∠3是同位角,故此选项不符合题意;
B、∠1和∠5不存在直接联系,故此选项符合题意;
C、∠1和∠2是同旁内角,故此选项不符合题意;
D、∠1和∠6是内错角,故此选项不符合题意;
故选B.
2、下列各组图形中,一个图形经过平移能得到另一个图形的是( )
A. B. C. D.
【答案】D
【解析】
解:各组图形中,选项D中的图形是一个图形经过平移能得到另一个图形,
故选:D.
3、如图,在△ABC中,BC边上的高为( )
A.AD B.BE C.BF D.CG
【答案】A
【解析】
解:根据三角形的高的定义,AD为△ABC中BC边上的高.
故选:A.
4、如图,能判定AB∥CD的条件是( )
A.∠2=∠B B.∠3=∠A C.∠1=∠A D.∠A=∠2
【答案】D
【解析】
根据内错角相等,两直线平行,
∵∠A=∠2,
∴AB∥CD,
故选:D.
5、如图,下列给定的条件中,不能判定的是( )
A. B. C. D.
【答案】A
【分析】
根据平行线的判定条件:同位角相等,两直线平行,同旁内角互补,两直线平行,内错角相等,两直线平行,进行逐一判断即可.
【详解】
解:A选项:当∠1=∠A时,可知是DE和AC被AB所截得到的同位角,可得到DE∥AC,而不是AB∥DF,故符合题意;
B选项:当∠A=∠3时,可知是AB、DF被AC所截得到的同位角,可得AB∥DF,故不符合题意;
C选项:当∠1=∠4时,可知是AB、DF被DE所截得到的内错角,可得AB∥DF,故不符合题意;
D选项:当∠2+∠A=180°时,是一对同旁内角,可得AB∥DF;故不符合题意;
故选A.
6、如图,下列条件能判断直线l1//l2有( )
①;②;③;④;⑤
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】
【分析】根据平行线的判定定理进行依次判断即可.
【详解】①∵∠1,∠3互为内错角,∠1=∠3,∴;
②∵∠2,∠4互为同旁内角,∠2+∠4=180° ,∴;
③∠4,∠5互为同位角,∠4=∠5,∴;
④∠2,∠3没有位置关系,故不能证明 ,
⑤,,
∴∠1=∠3,
∴,
故选D.
7、如图,把纸片沿折叠,当点落在四边形的外部时,此时测得,,则的度数为
A. B. C. D.
【分析】根据折叠性质得出,根据三角形外角性质得出,.
【解析】如图,设与交于点,
,,
,,
,
,.
故选:.
8、如图,若AB∥CD,CD∥EF,那么BCE=( )
A. 180°-2+1 B. 180°-1-2 C. 2=21 D. 1+2
【答案】A
【解析】
【分析】根据两直线平行,内错角相等,同旁内角互补,这两条性质解答.
【详解】∵AB∥CD,CD∥EF,
∴∠1=∠BCD,∠ECD+∠2=180°,
∴BCE=∠BCD+∠ECD=180°-2+1,
故选A.
9、如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3=( )
A.70° B.180° C.110° D.80°
【分析】法一:延长直线后根据平行线的性质解答即可;
法二:过∠2的顶点作直线b的平行线,由平行线的性质可求解.
【解答】解:法一:延长直线,如图:
,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故选:C.
法二:如图,过∠2的顶点作直线c∥b,
得∠3=∠4,
∴∠2﹣∠3=∠2﹣∠4,
∵a∥b,b∥c,
∴a∥c,
∴∠2﹣∠4=180°﹣∠1=180°﹣70°=110°,
即∠2﹣∠3=110°,
故选:C.
10、①如图1,AB∥CD,则∠A+∠E+∠C=180°;②如图2,AB∥CD,则∠E=∠A+∠C;③如图3,AB∥CD,则∠A+∠E﹣∠1=180°;④如图4,AB∥CD,则∠A=∠C+∠P.以上结论正确的个数是( )
A.1个 B.2个 C.3个 D.4个
【分析】①过点E作直线EF∥AB,由平行线的性质即可得出结论;
②过点E作直线EF∥AB,由平行线的性质即可得出结论;
③过点E作直线EF∥AB,由平行线的性质可得出∠A+∠E﹣∠1=180°;
④先根据三角形外角的性质得出∠1=∠C+∠P,再根据两直线平行,内错角相等即可作出判断.
【解答】解:①过点E作直线EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,
∴∠A+∠1=180°,∠2+∠C=180°,∴∠A+∠B+∠E=360°,故本小题错误;
②过点E作直线EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,∴∠A=∠1,∠2=∠C,
∴∠AEC=∠A+∠C,即∠E=∠A+∠C,故本小题正确;
③过点E作直线EF∥AB,
∵AB∥CD,∴AB∥CD∥EF,∴∠A+∠3=180°,∠1=∠2,
∴∠A+∠AEC﹣∠1=180°,即∠A+∠E﹣∠1=180°,故本选项正确;
④∵∠1是△CEP的外角,∴∠1=∠C+∠P,
∵AB∥CD,∴∠A=∠1,即∠A=∠C﹣∠P,故本小题正确.
综上所述,正确的小题有②③④共3个.
故选:C.
二、填空题
11、如图,在中,是的中点,将沿向右平移得△,若点平移的距离,则 .
【分析】利用平移的性质得到,然后根据是的中点可得到的长.
【解析】沿向右平移得△,
,
是的中点,
.
故答案为8.
12、已知从某个多边形的一个顶点出发一共画出4条对角线,那么这个多边形共有 条对角线.
【分析】根据对角线的概念,知一个多边形从一个顶点出发有条对角线,求出的值,再根据多边形对角线的总数为,即可解答.
【解析】从某个多边形的一个顶点出发一共画出4条对角线,
,
,
那么这个多边形对角线的总条数为:.
故答案为:14.
13、如图AB//CD,CE平分∠ACD交AB于E,∠A=128°,则∠AEC=______________.
【分析】首先根据ABCD,得到∠ACD=52°,再由CE平分∠ACD,得到∠ACE=∠DCE=26°,最后由两直线平行内错角相等,得到∠AEC=26°.
解:∵ABCD,∴∠AEC=∠DCE,∠A+∠ACD=180°,∴∠ACD=180°﹣∠A=180°﹣128°=52°,
∵CE平分∠ACD,∴∠ACE=∠DCE==26°,∴∠AEC=∠DCE=26°;
故答案为:26°.
14、如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=_____
【答案】105°
【解析】
解:由平移可知∠DEF=∠ABC=75°,
∵BE∥CF,
∴∠EFC=180°﹣∠DEF=180﹣75=105°
故答案是:105°.
15、如图,直线c与a,b相交,∠1=40°,∠2=70°,要使直线a与b平行,直线a顺时针旋转的度数至少是 °.
【分析】根据同位角相等两直线平行,求出旋转后∠2的同位角的度数,然后用∠3减去∠1即可得到直线a顺时针旋转的度数.
【解析】如图.
∵∠3=∠2=70°时,a∥b,
∴要使直线a与b平行,直线a顺时针旋转的度数至少是70°﹣40°=30°.
故答案为:30.
16、已知∠ABC=70°,点D为BC边上一点,过点D作DP∥AB,若∠PBD=∠ABC,则∠DPB= .
【分析】此题有两种情况,根据∠PBD=∠ABC,∠ABC=70°,得到∠PBD=35°,根据平行线的性质和三角形的外角的性质即可得到结论.
【解答】解:如图,∵∠PBD=∠ABC,∠ABC=70°,
∴∠PBD=35°,
∵PD∥AB,
∴∠P1DC=∠BDP2=70°,
∴∠DP1B=35°,∠DP2B=75°,
∴∠DPB=35°或75°,
故答案为:35°或75°.
17、如图,,则间的数量关系是_________.
【分析】分别过点P1、P2作P1C∥m,P2D∥m,由平行线的性质可知,∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,所以∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,∠CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
18、一副直角三角尺叠放如图所示,现将30°的三角尺固定不动,将45°的三角尺绕顶点B逆时针转动,点E始终在直线的上方,当两块三角尺至少有一组边互相平行时,则所有符合条件的度数为( )
A. 45°,75°,120°,165° B. 45°,60°,105°,135°
C. 15°,60°,105°,135° D. 30°,60°,90°,120°
【答案】A
【解析】
【分析】分DE∥AB,DE∥AC,BE∥AC,AC∥BD,分别画出图形,根据平行线性质和三角板的特点求解.
【详解】解:如图,
①DE∥AB,∴∠D+∠ABD=180°
∴∠ABD=90°∴∠ABE=45°;
②DE∥AC,
∵∠D=∠C=90°,∴B,C,D共线,
∴∠ABE=∠CBE+∠ABC=180°-45°+30°=165°;
③BE∥AC,∴∠C=∠CBE=90°,
∴∠ABE=∠ABC+∠CBE=120°;
④AC∥BD,
∴∠ABD=180°-∠A=120°,∴∠ABE=∠ABD-∠DBE=75°,
综上:∠ABE的度数为:45°或75°或120°或165°.
三、解答题
19、如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′,补全△A′B′C′;
(3)若连接AA′,BB′,则这两条线段之间的关系;
(4)在图中画出△ABC的高CD.
【答案】 解:(1)S△ABC=×5×4=10;
(2)如图所示:
(3)平行且相等;
(4)如图所示:
20、如图所示,∠1=65°,∠2=65°,∠3=115°,试说明DE//BC,DF//AB.
【答案】见解析
【解析】
解:∵∠1=65°,∠2=65°,
∴∠1=∠2,
∴DE∥BC ,
∵∠1=∠4=65°,∠3=115°,
∴∠3+∠4=65°+115°=180°,
∴DF∥AB.
21、如图所示,四边形ABCD中,ADC的角平分线DE与BCD的角平分线CA相交于E点,
已知:ACB=32°,CDE=58°.
(1)求DEC的度数;
(2)试说明直线
【答案】(1)90°;(2)见解析
【解析】
【分析】(1)根据三角形内角和定理即可求解;
(2)首先求得∠ADC的度数和∠DCB的度数,根据同旁内角互补,两直线平行即可证得.
【详解】解:(1)∵AC是BCD的平分线
∴
∵
∴∠DEC=180°-∠ACD-∠CDE=180°-32°-58°=90°;
(2)∵DE平分∠ADC,CA平分∠BCD
∴∠ADC=2∠CDE=116°,∠BCD=2∠ACD=64°
∵∠ADC+∠BCD=116°+64°=180°
∴
22、已知:如图,DB⊥AF于点G,EC⊥AF于点H,∠C=∠D.求证:∠A=∠F.
证明:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°( ).
∴DB∥EC( ).
∴∠C= ( ).
∵∠C=∠D(已知),
∴∠D= ( ).
∴DF∥AC( ).
∴∠A=∠F( ).
【答案】垂直的定义;同位角相等,两直线平行;∠DBA;两直线平行,同位角相等;∠DBA;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
【解析】
【分析】先证DB∥EC,得∠C=∠DBA,再证∠D=∠DBA,得DF∥AC,然后由平行线的性质即可得出结论.
【详解】解:∵DB⊥AF于点G,EC⊥AF于点H(已知),
∴∠DGH=∠EHF=90°(垂直的定义),
∴DB∥EC(同位角相等,两直线平行),
∴∠C=∠DBA(两直线平行,同位角相等),
∵∠C=∠D(已知),
∴∠D=∠DBA(等量代换),
∴DF∥AC(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠DBA,两直线平行,同位角相等;∠DBA,等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
23、如图,在△ABC中,∠BAC=90°,∠D=29°,BD平分∠ABC,CD∥AB交BD于点D,
求∠1的度数.
【分析】由平行线的性质可得∠ABD=∠D=29°,再由角平分线的定义得∠ABC=58°,结合∠BAC=90°,即可求∠1的度数.
解:∵CD∥AB,∴∠ABD=∠D=29°,
∵BD平分∠ABDC,∴∠ABC=2∠ABD=58°,
∵∠BAC=90°,∴∠1与∠ABC互余,
∴∠1=90°﹣58°=32°.
故∠1的度数为32°.
24、如图,把沿折叠,使点落在点处,
(1)若,试判断与的数量关系,并说明理由;
(2)若,求的度数.
【分析】(1)根据折叠的性质得到,根据平行线的性质得到,,所等量代换得到.
(2)根据三角形的内角和定理得到,根据折叠的性质得到,,所根据四边形的内角和等于得到,于是得到结论.
【解析】(1),理由如下:
是由翻折得到,,
,,,.
(2),,,
是由翻折得到,,,
,
,.
25、如图,在四边形中,与互补,、分别平分、,与相交于点.
(1)与有怎样的数量关系?说明理由;
(2)若,,求的度数.
【分析】(1)根据四边形的内角和为以及补角的定义可得,再根据角平分线的定义以及平行线的性质即可得出;
(2)根据与互补可得的度数,根据与互余可得的度数,根据平行线的性质可得的度数,然后根据三角形的内角和以及角的和差关系计算即可.
【解析】(1)与互余.
四边形的内角和为,与互补,
,
、分别平分、,,,
,,
,即与互余.
(2)由(1)知,,
,,与互补,,,
,,
平分,,
,.
26、如图1所示,MN//PQ,∠ABC与MN,PQ分别交于A、C两点
(1)若∠MAB=∠QCB=20°,则B的度数为 度.
(2)在图1分别作∠NAB与∠PCB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②若∠ABC=n°,求∠AFC的度数(用含有n的代数式表示);
(3)如图2所示,直线AE,CD相交于D点,且满足∠BAM=m∠MAE, ∠BCP=m∠DCP,试探究∠CDA与∠ABC的数量关系
【答案】(1)40;(2)①见解析;②;(3)m∠CDA+∠ABC=180°
【解析】
【分析】(1)作MN、PQ的平行线HG,根据两直线平行,内错角相等即可解答;
(2)①根据题意作图即可,②过F作 ,根据两直线平行,同旁内角互补和内错角相等即可解答;
(3)延长AE交PQ于点G,设∠MAE=x°,∠DCP=y°,知∠BAM=m∠MAE=mx°,∠BCP=m∠DCP=my°,∠BCQ=180° my°,根据(1)中所得结论知∠ABC=mx°+180° my°,即y° x°= ,由MNPQ知∠MAE=∠DGP=x°,根据∠CDA=∠DCP ∠DGC可得答案.
【详解】解:(1)作 ,
∵MN//PQ,∴,
∴ ,∴ ;
(2)①如图所示,
②过点F作 ,
∴ ,
∴ ,
∵ ,
∴ ,
∵∴ ,
∴ ,
∵ ,∴ ;
(3)延长AE交PQ于点G,
设∠MAE=x°,∠DCP=y°,则∠BAM=m∠MAE=mx°,∠BCP=m∠DCP=my°,
∴∠BCQ=180° my°,
由(1)知,∠ABC=mx°+180° my°,
∴y° x°=,
∵MNPQ,∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP ∠DGC=y° x°=,
即m∠CDA+∠ABC=180°.
(
1
)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
