课前预习练 第7章 平面图形的认识(二) 章末整合提升(1) -2021-2022学年七年级数学下册 (苏科版)
文档属性
| 名称 | 课前预习练 第7章 平面图形的认识(二) 章末整合提升(1) -2021-2022学年七年级数学下册 (苏科版) |  | |
| 格式 | docx | ||
| 文件大小 | 615.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 15:04:09 | ||
图片预览

文档简介
7章:平面图形的认识(二) 章末整合提升(1)【课前预习练】
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、如图,下列两个角是同旁内角的是( )
A.与 B.与 C.与 D.与
(1题) (5题) (7题)
2、下列图形不能通过平移变换得到的是( )
A. B. C. D.
3、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
4、若一个多边形的每个内角都等于与它相邻外角的2倍,则它的边数为( )
A.4 B.5 C.6 D.8
5、如图,下面哪个条件不能判断EF∥DC的是( )
A.∠1=∠2 B.∠4=∠C C.∠1+∠3=180° D.∠3+∠C=180°
6、一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
A.第一次向右拐40°,第二次向右拐140°. B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°. D.第一次向右拐140°,第二次向左拐40°.
7、如图所示,BE平分∠CBA,DE//BC,∠ADE=50°,则∠DEB的度数为( )
A.10° B.25° C.15° D.20°
8、如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
(8题) (9题) (10题)
9、如图,直线,∠2+∠3=210°,则∠1=( )
A.30° B.35° C.40° D.45°
10、如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,
则∠E= 度.
二、填空题
11、如图,∠3的同旁内角是________,∠2的同位角是_________.
12、一个多边形的内角和是它外角和的2倍,则它的边数是 .
13、如图,将三角形沿直线平移得到三角形,其中点与点是对应点,点与点是对应点,点与点是对应点.如果,,那么线段的长是_______.
(13题) (14题) (15题)
14、如图,已知,,则____________度
15、如图,,AE平分∠CAB交CD于点E,若,则___.
16、如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC= °.
(16题) (17题)
17、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
18、一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为().在旋转过程中,当两块三角板有两边平行时,的度数为______.
三、解答题
19、在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示,将先向右平移5格,再向上平移2格得△.
(1)画出平移后的△;
(2)画出的高(借助格点,留下作图痕迹);
(3)图中与的关系是 ;
(4)平移中线段扫过部分的面积是 .
20、已知:,点G在上,B、C、G三点在同一条直线上,且,,求证:.
21、如图,,,试求的度数.
22、推理填空:如图,直线,并且被直线所截,交和于点,平分,平分,使说明.
解:∵,
∴( )
∵平分,平分.
∴, ( )
∵
∴( )
∵
∴( )
23、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
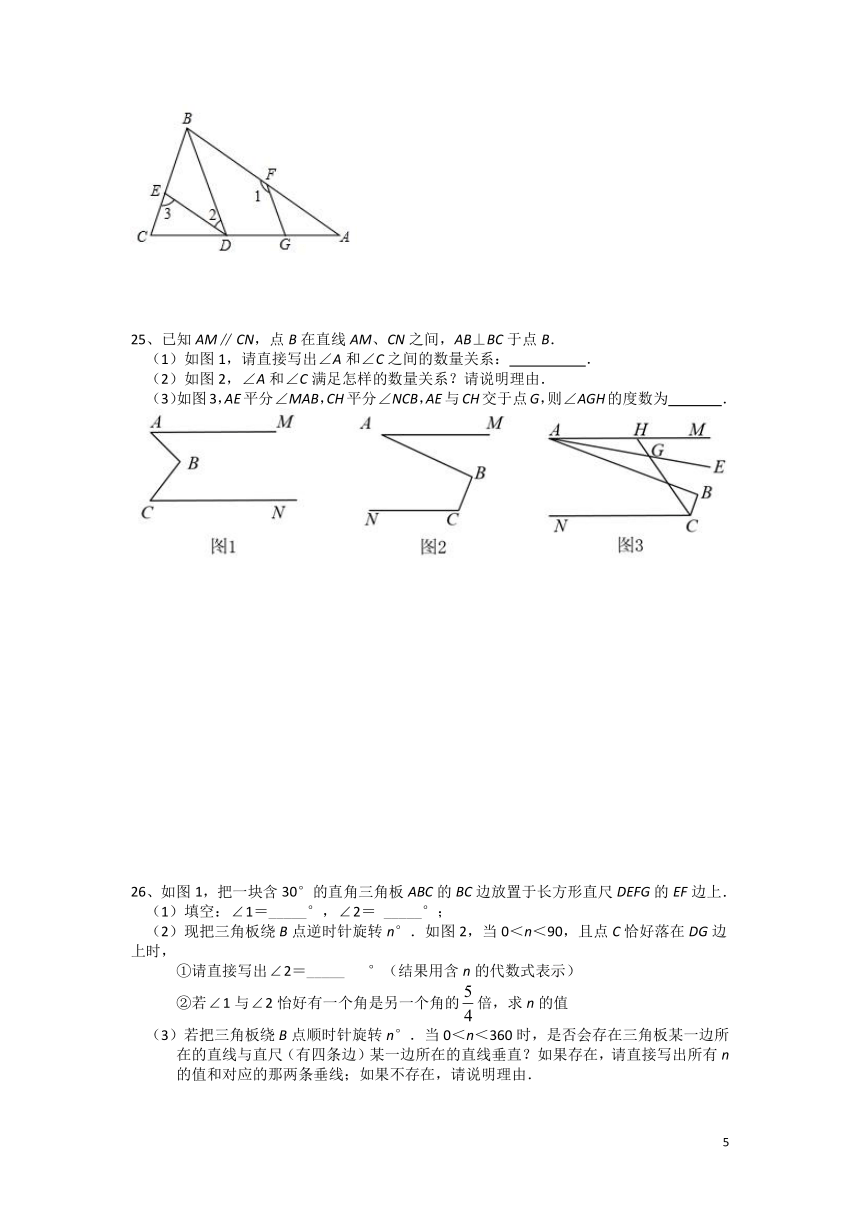
24、如图,点D、E、F、G均在的边上,连接BD、DE、FG,∠3=∠CBA,FG//BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
25、已知AMCN,点B在直线AM、CN之间,AB⊥BC于点B.
(1)如图1,请直接写出∠A和∠C之间的数量关系: .
(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.
(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 .
26、如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:1=_____°,2= _____°;
(2)现把三角板绕B点逆时针旋转n°.如图2,当0<n<90,且点C恰好落在DG边上时,
①请直接写出2=_____ °(结果用含n的代数式表示)
②若1与2怡好有一个角是另一个角的倍,求n的值
(3)若把三角板绕B点顺时针旋转n°.当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.
7章:平面图形的认识(二) 章末整合提升(1)
【课前预习练】-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、如图,下列两个角是同旁内角的是( )
A.与 B.与 C.与 D.与
【答案】B
【解析】
解:由图可知,∠1与∠3是同旁内角,
∠1与∠2是内错角,
∠4与∠2是同位角,
故选:B.
2、下列图形不能通过平移变换得到的是( )
A. B. C. D.
【答案】B
【解析】
解:根据平移的性质可知:不能用平移变换得到的是选项B,
故选:B.
3、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
【答案】C
【解析】解:AC边上的高就是过B作垂线垂直AC交AC于某点,因此只有选项C符合条件;
故选C.
4、若一个多边形的每个内角都等于与它相邻外角的2倍,则它的边数为( )
A.4 B.5 C.6 D.8
【解析】设边数为n,
∵多边形的内角和公式为:(n﹣2)×180°,∴多边形的每个内角为:,
∵多边形的外角和公式为:360°,∴多边形的每个外角为:,
∵一个多边形的每个内角都等于与它相邻外角的2倍,
∴=×2,∴n=6,故选:C.
5、如图,下面哪个条件不能判断EF∥DC的是( )
A.∠1=∠2 B.∠4=∠C C.∠1+∠3=180° D.∠3+∠C=180°
【答案】C
【解析】
选项A:因为∠1=∠2,所以EF∥DC,故本选项能判断EF∥DC;
选项B:因为∠4=∠C,所以EF∥DC,故本选项能判断EF∥DC;
选项C:因为∠1+∠3=180°,所以ED∥BC,故本选项能不判断EF∥DC;
选项D:因为∠3+∠C=180°,所以EF∥DC,故本选项能判断EF∥DC,
故选:C
6、一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
A.第一次向右拐40°,第二次向右拐140°. B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°. D.第一次向右拐140°,第二次向左拐40°.
【答案】B
【解析】
A.如图,由内错角相等可知,第二次拐弯后与原来平行,但方向相反,故不符合题意;
B.如图,由同位角相等可知,第二次拐弯后与原来平行,且方向相同,故符合题意;
C.如图,由内错角不相等可知,第二次拐弯后与原来不平行,故不符合题意;
D.如图,由同位角不相等可知,第二次拐弯后与原来不平行,故不符合题意.
故选:B.
7、如图所示,BE平分∠CBA,DE//BC,∠ADE=50°,则∠DEB的度数为( )
A.10° B.25° C.15° D.20°
【分析】先由平行线的性质得出∠ABC的度数,再由角平分线的性质得出∠EBC.
解:∵DE∥BC,∴∠ABC=∠ADE=50°,∠DEB=∠EBC,
∵BE是∠ABC的平分线,∴∠DEB=∠EBC= ∠ABC=25°.
故答案为:25.故选:B
8、如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】
根据平行线的判定定理进行依次判断即可.
【详解】
①∵∠1,∠3互为内错角,∠1=∠3,∴;
②∵∠2,∠4互为同旁内角,∠2+∠4=180° ,∴;
③∠4,∠5互为同位角,∠4=∠5,∴;
④∠2,∠3没有位置关系,故不能证明 ,
⑤,,
∴∠1=∠3,
∴,
故选D.
9、如图,直线,∠2+∠3=210°,则∠1=( )
A.30° B.35° C.40° D.45°
【分析】作,根据两直线平行内错角相等,得到,再由平行线的传递性得到,根据两直线平行同旁内角互补,得到,结合题目已知条件可证,解得的度数即可解得的度数.
解:如图,作,,
,∠2+∠3=210°,
,故选:A.
10、如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,
则∠E= 度.
【分析】设∠EPC=2x,∠EBA=2y,根据角平分线的性质得到∠CPF=∠EPF=x,∠EBF=∠FBA=y,根据外角的性质得到∠1=∠F+∠ABF=42°+y,∠2=∠EBA+∠E=2y+∠E,由平行线的性质得到∠1=∠CPF=x,∠2=∠EPC=2x,于是得到方程2y+∠E=2(42°+y),即可得到结论.
【解答】解:设∠EPC=2x,∠EBA=2y,
∵∠EBA、∠EPC的角平分线交于点F
∴∠CPF=∠EPF=x,∠EBF=∠FBA=y,
∵∠1=∠F+∠ABF=40°+y,
∠2=∠EBA+∠E=2y+∠E,
∵AB∥CD,
∴∠1=∠CPF=x,∠2=∠EPC=2x,
∴∠2=2∠1,
∴2y+∠E=2(40°+y),
∴∠E=80°.
故答案为:80.
二、填空题
11、如图,∠3的同旁内角是________,∠2的同位角是_________.
【分析】根据同位角,同旁内角的定义逐个判断即可.
解:∠3的同旁内角是∠8, ∠2的同位角是∠5,
故答案为:∠8,∠5.
12、一个多边形的内角和是它外角和的2倍,则它的边数是 .
【分析】根据多边形的内角和公式以及外角和定理列出方程,然后求解即可.
【解析】设这个多边形的边数是,
根据题意得,,
解得.
答:这个多边形的边数是6.
故答案为:6.
13、如图,将三角形沿直线平移得到三角形,其中点与点是对应点,点与点是对应点,点与点是对应点.如果,,那么线段的长是_______.
【答案】3
【解析】
解:根据平移的性质可得:BE=CF
∵BE=BC-EC,,,
∴CF=BE=5-2=3,,
故答案为:3
14、如图,已知,,则____________度
【分析】结合题意,根据平行线的判定定理,得,从而得到,结合,通过计算,即可得到答案.
解:∵∴ ∴
∵,∴
故答案为:110.
15、如图,,AE平分∠CAB交CD于点E,若,则___.
【分析】根据,证得,,求出,利用AE平分∠CAB,求得,计算即可得解.
解:∵,∴,,
∵,∴,
∵AE平分∠CAB,∴,∴,
故答案为:125°.
16、如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC= °.
【分析】根据平行线的性质,先求出∠BEF和∠CEF的度数,再求出它们的差即可.
【解答】解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°﹣∠ECD=180°﹣150°=30°,
∴∠BEC=∠BEF﹣∠CEF=40°;
故答案为:40.
17、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
【答案】
【解析】
解:∵AD为△ABC中线
∴S△ABD=S△ACD,
又∵E为AD中点,
故,
∴,
∵BF为△BEC中线,
∴cm2.
故答案为:1cm2.
18、一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为().在旋转过程中,当两块三角板有两边平行时,的度数为______.
【分析】分五种情况进行讨论,分别依据平行线的性质进行计算即可得到∠α的度数.
解:①当CD∥OB时,∠α=∠D=30°
②当OC∥AB时,∠OEB=∠COD=90°,此时∠α=90°-∠B=90°-45°=45°
③当DC∥OA时,∠DOA=∠D=30°,此时∠α=∠AOB+∠AOD=90°+30°=120°
④当OD∥AB时,∠AOD=∠A=45°,此时∠α=∠A+∠AOD=90°+45°=135°
⑤当CD∥AB时,延长BO交CD于点E,则∠CEO=∠B=45°
∴∠DEO=180°-∠CEO=135°, ∴∠DOE=180°-∠DEO-∠D=15°
此时∠α=180°-∠DOE=180°-15°=165°
综上,在旋转过程中,当两块三角板有两边平行时,的度数为30°或45°或120°或135°或165°
三、解答题
19、在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示,将先向右平移5格,再向上平移2格得△.
(1)画出平移后的△;
(2)画出的高(借助格点,留下作图痕迹);
(3)图中与的关系是 ;
(4)平移中线段扫过部分的面积是 .
【分析】(1)利用平移变换的性质分别作出,,的对应点,,即可.
(2)根据三角形的高的定义,画出图形即可.
(3)利用平移变换的性质判断即可.
(4)平移中线段扫过部分的面积是两个平行四边形的面积之和.
【解析】(1)如图,△即为所求.
(2)如图,线段即为所求.
(3)图中与的关系是,.
故答案为:,.
(4)平移中线段扫过部分的面积是.
20、已知:,点G在上,B、C、G三点在同一条直线上,且,,求证:.
【答案】见解析
【解析】
证明:,,、、三点在同一条直线上,
,
,
又,
.
21、如图,,,试求的度数.
【分析】由题意可直接证得AB∥CD,得到∠BAP=∠APC,结合∠1=∠2,可得∠EAP=∠APF,从而得到AE∥FP,最终得到∠E=∠F,即可得到答案.
【详解】∵∠BAP+∠APD=180°,∴AB∥CD,∴∠BAP=∠APC,
∵∠1=∠2,∴∠BAP-∠1=∠APC-∠2,即:∠EAP=∠APF,
∴AE∥FP,∴∠E=∠F,∴∠F=40°.
22、推理填空:如图,直线,并且被直线所截,交和于点,平分,平分,使说明.
解:∵,
∴( )
∵平分,平分.
∴, ( )
∵
∴( )
∵
∴( )
【答案】两直线平行,同位角相等;∠CNE,角平分线的定义;等量代换;同位角相等,两直线平行.
【解析】
【分析】利用平行线的性质定理和判定定理解答即可.
【详解】解:∵AB∥CD,
∴∠AME=∠CNE.(两直线平行,同位角相等),
∵MP平分∠AME,NQ平分∠CNE,
∴∠1=∠AME,=∠CNE.( 角平分线的定义),
∵∠AME=∠CNE,
∴∠1=∠2.(等量代换),
∵∠1=∠2,
∴MP∥NQ.(同位角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠CNE,角平分线的定义;等量代换;同位角相等,两直线平行.
23、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
【答案】⑴4.8cm;⑵12cm ;⑶2cm.
【解析】
∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD= =4.8(cm),
即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm.
24、如图,点D、E、F、G均在的边上,连接BD、DE、FG,∠3=∠CBA,FG//BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
【答案】(1)见解析;(2)75°
【解析】解:(1)∵∠3=∠CBA,
∴DE∥AB,
∴∠2=∠DBA,
∵FG//BD,
∴∠DBA+∠1=180°
∴∠1+∠2=180°;
(2)由(1)得DE∥AB,∠2=∠DBA,
∵∠A=35°,
∴∠EDC=∠A=35°,
∵DE平分∠BDC,
∴∠EDC=∠2=35°,
∴∠DBA=35°,
∵BD平分∠ABC
∴∠ABC=2∠DAB=70°
∵∠A+∠C+∠ABC=180°
∴∠C=180°-∠A-∠ABC=75°
25、已知AMCN,点B在直线AM、CN之间,AB⊥BC于点B.
(1)如图1,请直接写出∠A和∠C之间的数量关系: .
(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.
(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 .
【答案】(1)∠A+∠C=90°;(2)∠C﹣∠A=90°,见解析;(3)45°
【解析】
【分析】(1)过点B作BE∥AM,利用平行线的性质即可求得结论;
(2)过点B作BE∥AM,利用平行线的性质即可求得结论;
(3)利用(2)的结论和三角形的外角等于和它不相邻的两个内角的和即可求得结论.
【详解】(1)过点B作BE∥AM,如图,
∵BE∥AM,∴∠A=∠ABE,
∵BE∥AM,AM∥CN,∴BE∥CN,∴∠C=∠CBE,
∵AB⊥BC,∴∠ABC=90°,∴∠A+∠C=∠ABE+∠CBE=∠ABC=90°.
故答案为:∠A+∠C=90°;
(2)∠A和∠C满足:∠C﹣∠A=90°.理由:
过点B作BE∥AM,如图,
∵BE∥AM,∴∠A=∠ABE,
∵BE∥AM,AM∥CN,∴BE∥CN,∴∠C+∠CBE=180°,∴∠CBE=180°﹣∠C,
∵AB⊥BC,∴∠ABC=90°,∴∠ABE+∠CBE=90°,
∴∠A+180°﹣∠C=90°,∴∠C﹣∠A=90°;
(3)设CH与AB交于点F,如图,
∵AE平分∠MAB,∴∠GAF=∠MAB,
∵CH平分∠NCB,∴∠BCF=∠BCN,
∵∠B=90°,∴∠BFC=90°﹣∠BCF,
∵∠AFG=∠BFC,∴∠AFG=90°﹣∠BCF.
∵∠AGH=∠GAF+∠AFG,∴∠AGH=∠MAB+90°﹣∠BCN=90°﹣(∠BCN﹣∠MAB).
由(2)知:∠BCN﹣∠MAB=90°,∴∠AGH=90°﹣45°=45°.
故答案为:45°.
26、如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:1=_____°,2= _____°;
(2)现把三角板绕B点逆时针旋转n°.如图2,当0<n<90,且点C恰好落在DG边上时,
①请直接写出2=_____ °(结果用含n的代数式表示)
②若1与2怡好有一个角是另一个角的倍,求n的值
(3)若把三角板绕B点顺时针旋转n°.当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.
【答案】(1)120°,90°;(2)①90°+n°;②n的值为或;(3)当n=30°时,AB⊥DG(EF);当n=90°时,BC⊥DG(EF),AC⊥DE(GF);当n=120°时,AB⊥DE(GF);当n=180°时,AC⊥DG (EF),BC⊥DE(GF);当n=210°时,AB⊥DG (EF);当n=270°时,BC⊥DG (EF),AC⊥DE(GF);当n=300°时,AB⊥DE (GF).
【解析】
【分析】(1)根据邻补角的定义和平行线的性质解答;
(2)①根据两直线平行,同旁内角互补求出∠BCG,然后根据周角等于360°计算即可得到∠2;②根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相等可得∠1=∠ABE,再分∠1=∠2和∠2=∠1分别求解即可;
(3)结合图形,分AB、BC、AC三条边与直尺垂直讨论求解.
【详解】解:(1)∠1=180° 60°=120°,∠2=90°;
故答案为:120,90;
(2)①如图2,∵DG∥EF,∴∠BCG=180° ∠CBF=180° n°,
∵∠ACB+∠BCG+∠2=360°,
∴∠2=360° ∠ACB ∠BCG=360° 90° (180° n°)=90°+n°;
故答案为:90°+n°;
②∵∠ABC=60°,∴∠ABE=180° 60° n°=120° n°,
∵DG∥EF,∴∠1=∠ABE=120° n°,
若∠1=∠2,则120° n°=(90°+n°),解得n=;
若∠2=∠1,则90°+n°=(120° n°),解得n=;
所以n的值为或;
(3)当n=30°时,AB⊥DG(EF);
当n=90°时,BC⊥DG(EF),AC⊥DE(GF);
当n=120°时,AB⊥DE(GF);
当n=180°时,AC⊥DG (EF),BC⊥DE(GF);
当n=210°时,AB⊥DG (EF);
当n=270°时,BC⊥DG (EF),AC⊥DE(GF);
当n=300°时,AB⊥DE (GF).
(
1
)
-2021-2022学年七年级数学下册 (苏科版)
一、选择题
1、如图,下列两个角是同旁内角的是( )
A.与 B.与 C.与 D.与
(1题) (5题) (7题)
2、下列图形不能通过平移变换得到的是( )
A. B. C. D.
3、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
4、若一个多边形的每个内角都等于与它相邻外角的2倍,则它的边数为( )
A.4 B.5 C.6 D.8
5、如图,下面哪个条件不能判断EF∥DC的是( )
A.∠1=∠2 B.∠4=∠C C.∠1+∠3=180° D.∠3+∠C=180°
6、一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
A.第一次向右拐40°,第二次向右拐140°. B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°. D.第一次向右拐140°,第二次向左拐40°.
7、如图所示,BE平分∠CBA,DE//BC,∠ADE=50°,则∠DEB的度数为( )
A.10° B.25° C.15° D.20°
8、如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
(8题) (9题) (10题)
9、如图,直线,∠2+∠3=210°,则∠1=( )
A.30° B.35° C.40° D.45°
10、如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,
则∠E= 度.
二、填空题
11、如图,∠3的同旁内角是________,∠2的同位角是_________.
12、一个多边形的内角和是它外角和的2倍,则它的边数是 .
13、如图,将三角形沿直线平移得到三角形,其中点与点是对应点,点与点是对应点,点与点是对应点.如果,,那么线段的长是_______.
(13题) (14题) (15题)
14、如图,已知,,则____________度
15、如图,,AE平分∠CAB交CD于点E,若,则___.
16、如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC= °.
(16题) (17题)
17、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
18、一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为().在旋转过程中,当两块三角板有两边平行时,的度数为______.
三、解答题
19、在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示,将先向右平移5格,再向上平移2格得△.
(1)画出平移后的△;
(2)画出的高(借助格点,留下作图痕迹);
(3)图中与的关系是 ;
(4)平移中线段扫过部分的面积是 .
20、已知:,点G在上,B、C、G三点在同一条直线上,且,,求证:.
21、如图,,,试求的度数.
22、推理填空:如图,直线,并且被直线所截,交和于点,平分,平分,使说明.
解:∵,
∴( )
∵平分,平分.
∴, ( )
∵
∴( )
∵
∴( )
23、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
24、如图,点D、E、F、G均在的边上,连接BD、DE、FG,∠3=∠CBA,FG//BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
25、已知AMCN,点B在直线AM、CN之间,AB⊥BC于点B.
(1)如图1,请直接写出∠A和∠C之间的数量关系: .
(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.
(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 .
26、如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:1=_____°,2= _____°;
(2)现把三角板绕B点逆时针旋转n°.如图2,当0<n<90,且点C恰好落在DG边上时,
①请直接写出2=_____ °(结果用含n的代数式表示)
②若1与2怡好有一个角是另一个角的倍,求n的值
(3)若把三角板绕B点顺时针旋转n°.当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.
7章:平面图形的认识(二) 章末整合提升(1)
【课前预习练】-2021-2022学年七年级数学下册 (苏科版)(解析)
一、选择题
1、如图,下列两个角是同旁内角的是( )
A.与 B.与 C.与 D.与
【答案】B
【解析】
解:由图可知,∠1与∠3是同旁内角,
∠1与∠2是内错角,
∠4与∠2是同位角,
故选:B.
2、下列图形不能通过平移变换得到的是( )
A. B. C. D.
【答案】B
【解析】
解:根据平移的性质可知:不能用平移变换得到的是选项B,
故选:B.
3、在下列各图中,正确画出AC边上的高的图形是( )
A.B.C.D.
【答案】C
【解析】解:AC边上的高就是过B作垂线垂直AC交AC于某点,因此只有选项C符合条件;
故选C.
4、若一个多边形的每个内角都等于与它相邻外角的2倍,则它的边数为( )
A.4 B.5 C.6 D.8
【解析】设边数为n,
∵多边形的内角和公式为:(n﹣2)×180°,∴多边形的每个内角为:,
∵多边形的外角和公式为:360°,∴多边形的每个外角为:,
∵一个多边形的每个内角都等于与它相邻外角的2倍,
∴=×2,∴n=6,故选:C.
5、如图,下面哪个条件不能判断EF∥DC的是( )
A.∠1=∠2 B.∠4=∠C C.∠1+∠3=180° D.∠3+∠C=180°
【答案】C
【解析】
选项A:因为∠1=∠2,所以EF∥DC,故本选项能判断EF∥DC;
选项B:因为∠4=∠C,所以EF∥DC,故本选项能判断EF∥DC;
选项C:因为∠1+∠3=180°,所以ED∥BC,故本选项能不判断EF∥DC;
选项D:因为∠3+∠C=180°,所以EF∥DC,故本选项能判断EF∥DC,
故选:C
6、一辆汽车在广阔的草原上行驶,两次拐弯后,行驶的方向与原来的方向相同,那么这两次拐弯的角度可能是( )
A.第一次向右拐40°,第二次向右拐140°. B.第一次向右拐40°,第二次向左拐40°.
C.第一次向左拐40°,第二次向右拐140°. D.第一次向右拐140°,第二次向左拐40°.
【答案】B
【解析】
A.如图,由内错角相等可知,第二次拐弯后与原来平行,但方向相反,故不符合题意;
B.如图,由同位角相等可知,第二次拐弯后与原来平行,且方向相同,故符合题意;
C.如图,由内错角不相等可知,第二次拐弯后与原来不平行,故不符合题意;
D.如图,由同位角不相等可知,第二次拐弯后与原来不平行,故不符合题意.
故选:B.
7、如图所示,BE平分∠CBA,DE//BC,∠ADE=50°,则∠DEB的度数为( )
A.10° B.25° C.15° D.20°
【分析】先由平行线的性质得出∠ABC的度数,再由角平分线的性质得出∠EBC.
解:∵DE∥BC,∴∠ABC=∠ADE=50°,∠DEB=∠EBC,
∵BE是∠ABC的平分线,∴∠DEB=∠EBC= ∠ABC=25°.
故答案为:25.故选:B
8、如图,下列条件能判断直线l1//l2的有( )
①;②;③;④;⑤
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】
根据平行线的判定定理进行依次判断即可.
【详解】
①∵∠1,∠3互为内错角,∠1=∠3,∴;
②∵∠2,∠4互为同旁内角,∠2+∠4=180° ,∴;
③∠4,∠5互为同位角,∠4=∠5,∴;
④∠2,∠3没有位置关系,故不能证明 ,
⑤,,
∴∠1=∠3,
∴,
故选D.
9、如图,直线,∠2+∠3=210°,则∠1=( )
A.30° B.35° C.40° D.45°
【分析】作,根据两直线平行内错角相等,得到,再由平行线的传递性得到,根据两直线平行同旁内角互补,得到,结合题目已知条件可证,解得的度数即可解得的度数.
解:如图,作,,
,∠2+∠3=210°,
,故选:A.
10、如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,
则∠E= 度.
【分析】设∠EPC=2x,∠EBA=2y,根据角平分线的性质得到∠CPF=∠EPF=x,∠EBF=∠FBA=y,根据外角的性质得到∠1=∠F+∠ABF=42°+y,∠2=∠EBA+∠E=2y+∠E,由平行线的性质得到∠1=∠CPF=x,∠2=∠EPC=2x,于是得到方程2y+∠E=2(42°+y),即可得到结论.
【解答】解:设∠EPC=2x,∠EBA=2y,
∵∠EBA、∠EPC的角平分线交于点F
∴∠CPF=∠EPF=x,∠EBF=∠FBA=y,
∵∠1=∠F+∠ABF=40°+y,
∠2=∠EBA+∠E=2y+∠E,
∵AB∥CD,
∴∠1=∠CPF=x,∠2=∠EPC=2x,
∴∠2=2∠1,
∴2y+∠E=2(40°+y),
∴∠E=80°.
故答案为:80.
二、填空题
11、如图,∠3的同旁内角是________,∠2的同位角是_________.
【分析】根据同位角,同旁内角的定义逐个判断即可.
解:∠3的同旁内角是∠8, ∠2的同位角是∠5,
故答案为:∠8,∠5.
12、一个多边形的内角和是它外角和的2倍,则它的边数是 .
【分析】根据多边形的内角和公式以及外角和定理列出方程,然后求解即可.
【解析】设这个多边形的边数是,
根据题意得,,
解得.
答:这个多边形的边数是6.
故答案为:6.
13、如图,将三角形沿直线平移得到三角形,其中点与点是对应点,点与点是对应点,点与点是对应点.如果,,那么线段的长是_______.
【答案】3
【解析】
解:根据平移的性质可得:BE=CF
∵BE=BC-EC,,,
∴CF=BE=5-2=3,,
故答案为:3
14、如图,已知,,则____________度
【分析】结合题意,根据平行线的判定定理,得,从而得到,结合,通过计算,即可得到答案.
解:∵∴ ∴
∵,∴
故答案为:110.
15、如图,,AE平分∠CAB交CD于点E,若,则___.
【分析】根据,证得,,求出,利用AE平分∠CAB,求得,计算即可得解.
解:∵,∴,,
∵,∴,
∵AE平分∠CAB,∴,∴,
故答案为:125°.
16、如图,已知AB,CD,EF互相平行,且∠ABE=70°,∠ECD=150°,则∠BEC= °.
【分析】根据平行线的性质,先求出∠BEF和∠CEF的度数,再求出它们的差即可.
【解答】解:∵AB∥EF,
∴∠BEF=∠ABE=70°;
又∵EF∥CD,
∴∠CEF=180°﹣∠ECD=180°﹣150°=30°,
∴∠BEC=∠BEF﹣∠CEF=40°;
故答案为:40.
17、如图,在中,已知点,,分别为,,的中点,且,
则阴影部分的面积______.
【答案】
【解析】
解:∵AD为△ABC中线
∴S△ABD=S△ACD,
又∵E为AD中点,
故,
∴,
∵BF为△BEC中线,
∴cm2.
故答案为:1cm2.
18、一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为().在旋转过程中,当两块三角板有两边平行时,的度数为______.
【分析】分五种情况进行讨论,分别依据平行线的性质进行计算即可得到∠α的度数.
解:①当CD∥OB时,∠α=∠D=30°
②当OC∥AB时,∠OEB=∠COD=90°,此时∠α=90°-∠B=90°-45°=45°
③当DC∥OA时,∠DOA=∠D=30°,此时∠α=∠AOB+∠AOD=90°+30°=120°
④当OD∥AB时,∠AOD=∠A=45°,此时∠α=∠A+∠AOD=90°+45°=135°
⑤当CD∥AB时,延长BO交CD于点E,则∠CEO=∠B=45°
∴∠DEO=180°-∠CEO=135°, ∴∠DOE=180°-∠DEO-∠D=15°
此时∠α=180°-∠DOE=180°-15°=165°
综上,在旋转过程中,当两块三角板有两边平行时,的度数为30°或45°或120°或135°或165°
三、解答题
19、在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示,将先向右平移5格,再向上平移2格得△.
(1)画出平移后的△;
(2)画出的高(借助格点,留下作图痕迹);
(3)图中与的关系是 ;
(4)平移中线段扫过部分的面积是 .
【分析】(1)利用平移变换的性质分别作出,,的对应点,,即可.
(2)根据三角形的高的定义,画出图形即可.
(3)利用平移变换的性质判断即可.
(4)平移中线段扫过部分的面积是两个平行四边形的面积之和.
【解析】(1)如图,△即为所求.
(2)如图,线段即为所求.
(3)图中与的关系是,.
故答案为:,.
(4)平移中线段扫过部分的面积是.
20、已知:,点G在上,B、C、G三点在同一条直线上,且,,求证:.
【答案】见解析
【解析】
证明:,,、、三点在同一条直线上,
,
,
又,
.
21、如图,,,试求的度数.
【分析】由题意可直接证得AB∥CD,得到∠BAP=∠APC,结合∠1=∠2,可得∠EAP=∠APF,从而得到AE∥FP,最终得到∠E=∠F,即可得到答案.
【详解】∵∠BAP+∠APD=180°,∴AB∥CD,∴∠BAP=∠APC,
∵∠1=∠2,∴∠BAP-∠1=∠APC-∠2,即:∠EAP=∠APF,
∴AE∥FP,∴∠E=∠F,∴∠F=40°.
22、推理填空:如图,直线,并且被直线所截,交和于点,平分,平分,使说明.
解:∵,
∴( )
∵平分,平分.
∴, ( )
∵
∴( )
∵
∴( )
【答案】两直线平行,同位角相等;∠CNE,角平分线的定义;等量代换;同位角相等,两直线平行.
【解析】
【分析】利用平行线的性质定理和判定定理解答即可.
【详解】解:∵AB∥CD,
∴∠AME=∠CNE.(两直线平行,同位角相等),
∵MP平分∠AME,NQ平分∠CNE,
∴∠1=∠AME,=∠CNE.( 角平分线的定义),
∵∠AME=∠CNE,
∴∠1=∠2.(等量代换),
∵∠1=∠2,
∴MP∥NQ.(同位角相等,两直线平行).
故答案为:两直线平行,同位角相等;∠CNE,角平分线的定义;等量代换;同位角相等,两直线平行.
23、如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.
【答案】⑴4.8cm;⑵12cm ;⑶2cm.
【解析】
∵∠BAC=90°,AD是边BC上的高,
∴AB AC=BC AD,
∴AD= =4.8(cm),
即AD的长度为4.8cm;
(2)如图,∵△ABC是直角三角形,∠BAC=90°,AB=6cm,AC=8cm,
∴S△ABC=AB AC=×6×8=24(cm2).
又∵AE是边BC的中线,
∴BE=EC,
∴BE AD=EC AD,即S△ABE=S△AEC,
∴S△ABE=S△ABC=12(cm2).
∴△ABE的面积是12cm2.
(3)∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+CE-(AB+BE+AE)=AC-AB=8-6=2(cm),
即△ACE和△ABE的周长的差是2cm.
24、如图,点D、E、F、G均在的边上,连接BD、DE、FG,∠3=∠CBA,FG//BD.
(1)求证:∠1+∠2=180°;
(2)若BD平分∠CBA,DE平分∠BDC,∠A=35°,求∠C的度数.
【答案】(1)见解析;(2)75°
【解析】解:(1)∵∠3=∠CBA,
∴DE∥AB,
∴∠2=∠DBA,
∵FG//BD,
∴∠DBA+∠1=180°
∴∠1+∠2=180°;
(2)由(1)得DE∥AB,∠2=∠DBA,
∵∠A=35°,
∴∠EDC=∠A=35°,
∵DE平分∠BDC,
∴∠EDC=∠2=35°,
∴∠DBA=35°,
∵BD平分∠ABC
∴∠ABC=2∠DAB=70°
∵∠A+∠C+∠ABC=180°
∴∠C=180°-∠A-∠ABC=75°
25、已知AMCN,点B在直线AM、CN之间,AB⊥BC于点B.
(1)如图1,请直接写出∠A和∠C之间的数量关系: .
(2)如图2,∠A和∠C满足怎样的数量关系?请说明理由.
(3)如图3,AE平分∠MAB,CH平分∠NCB,AE与CH交于点G,则∠AGH的度数为 .
【答案】(1)∠A+∠C=90°;(2)∠C﹣∠A=90°,见解析;(3)45°
【解析】
【分析】(1)过点B作BE∥AM,利用平行线的性质即可求得结论;
(2)过点B作BE∥AM,利用平行线的性质即可求得结论;
(3)利用(2)的结论和三角形的外角等于和它不相邻的两个内角的和即可求得结论.
【详解】(1)过点B作BE∥AM,如图,
∵BE∥AM,∴∠A=∠ABE,
∵BE∥AM,AM∥CN,∴BE∥CN,∴∠C=∠CBE,
∵AB⊥BC,∴∠ABC=90°,∴∠A+∠C=∠ABE+∠CBE=∠ABC=90°.
故答案为:∠A+∠C=90°;
(2)∠A和∠C满足:∠C﹣∠A=90°.理由:
过点B作BE∥AM,如图,
∵BE∥AM,∴∠A=∠ABE,
∵BE∥AM,AM∥CN,∴BE∥CN,∴∠C+∠CBE=180°,∴∠CBE=180°﹣∠C,
∵AB⊥BC,∴∠ABC=90°,∴∠ABE+∠CBE=90°,
∴∠A+180°﹣∠C=90°,∴∠C﹣∠A=90°;
(3)设CH与AB交于点F,如图,
∵AE平分∠MAB,∴∠GAF=∠MAB,
∵CH平分∠NCB,∴∠BCF=∠BCN,
∵∠B=90°,∴∠BFC=90°﹣∠BCF,
∵∠AFG=∠BFC,∴∠AFG=90°﹣∠BCF.
∵∠AGH=∠GAF+∠AFG,∴∠AGH=∠MAB+90°﹣∠BCN=90°﹣(∠BCN﹣∠MAB).
由(2)知:∠BCN﹣∠MAB=90°,∴∠AGH=90°﹣45°=45°.
故答案为:45°.
26、如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:1=_____°,2= _____°;
(2)现把三角板绕B点逆时针旋转n°.如图2,当0<n<90,且点C恰好落在DG边上时,
①请直接写出2=_____ °(结果用含n的代数式表示)
②若1与2怡好有一个角是另一个角的倍,求n的值
(3)若把三角板绕B点顺时针旋转n°.当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.
【答案】(1)120°,90°;(2)①90°+n°;②n的值为或;(3)当n=30°时,AB⊥DG(EF);当n=90°时,BC⊥DG(EF),AC⊥DE(GF);当n=120°时,AB⊥DE(GF);当n=180°时,AC⊥DG (EF),BC⊥DE(GF);当n=210°时,AB⊥DG (EF);当n=270°时,BC⊥DG (EF),AC⊥DE(GF);当n=300°时,AB⊥DE (GF).
【解析】
【分析】(1)根据邻补角的定义和平行线的性质解答;
(2)①根据两直线平行,同旁内角互补求出∠BCG,然后根据周角等于360°计算即可得到∠2;②根据邻补角的定义求出∠ABE,再根据两直线平行,同位角相等可得∠1=∠ABE,再分∠1=∠2和∠2=∠1分别求解即可;
(3)结合图形,分AB、BC、AC三条边与直尺垂直讨论求解.
【详解】解:(1)∠1=180° 60°=120°,∠2=90°;
故答案为:120,90;
(2)①如图2,∵DG∥EF,∴∠BCG=180° ∠CBF=180° n°,
∵∠ACB+∠BCG+∠2=360°,
∴∠2=360° ∠ACB ∠BCG=360° 90° (180° n°)=90°+n°;
故答案为:90°+n°;
②∵∠ABC=60°,∴∠ABE=180° 60° n°=120° n°,
∵DG∥EF,∴∠1=∠ABE=120° n°,
若∠1=∠2,则120° n°=(90°+n°),解得n=;
若∠2=∠1,则90°+n°=(120° n°),解得n=;
所以n的值为或;
(3)当n=30°时,AB⊥DG(EF);
当n=90°时,BC⊥DG(EF),AC⊥DE(GF);
当n=120°时,AB⊥DE(GF);
当n=180°时,AC⊥DG (EF),BC⊥DE(GF);
当n=210°时,AB⊥DG (EF);
当n=270°时,BC⊥DG (EF),AC⊥DE(GF);
当n=300°时,AB⊥DE (GF).
(
1
)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
