5.2.2 平行线的判定 同步练习(含答案)
文档属性
| 名称 | 5.2.2 平行线的判定 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 133.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 16:13:15 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第五章 相交线与平行线
5.2.2 平行线的判定
一、选择题
1.如图所示,能说明AD∥BC,下列条件成立的是( )
A.∠2=∠3 B.∠1=∠4
C.∠1+∠2=∠3+∠4 D.∠A+∠C=180°
2.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC B.BC∥CD
C.AB∥DC D.AB与CD相交
3.下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
4.如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的定理是( )
A.同位角相等两直线平行 B.同旁内角互补,两直线平行
C.内错角相等两直线平行 D.平行于同一条直线的两直线平行
5.如图,下列条件中,不能判断直线 ∥ 的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
填空题
如图所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
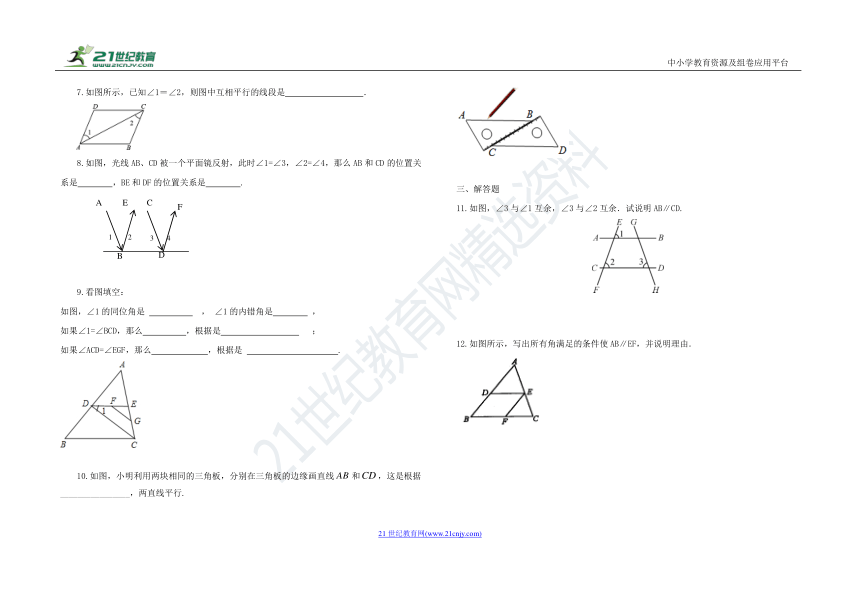
7.如图所示,已知∠1=∠2,则图中互相平行的线段是 .
8.如图,光线AB、CD被一个平面镜反射,此时∠1=∠3,∠2=∠4,那么AB和CD的位置关系是 ,BE和DF的位置关系是 .
(
B
A
C
D
E
F
1
2
3
4
)
9.看图填空:
如图,∠1的同位角是 , ∠1的内错角是 ,
如果∠1=∠BCD,那么 ,根据是 ;
如果∠ACD=∠EGF,那么 ,根据是 .
10.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线和,这是根据________________,两直线平行.
三、解答题
11.如图,∠3与∠1互余,∠3与∠2互余.试说明AB∥CD.
12.如图所示,写出所有角满足的条件使AB∥EF,并说明理由.
13.将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
14.如图,∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,那么AB∥CD,AD∥BC.请说明理由.
15.如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600,∠E=30°,试说明AB∥CD.
16.如图,∠1=∠3,∠1=∠2,那么DE与BC有怎样的位置关系?为什么?
17.如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).
18.(1)如图(1)所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.
判断AB与CD的位置关系,并说明理由;
(2)如图(2)所示在(1)的条件下,若小路OM平分∠EOB.通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N位置关系.
参考答案:
一、1.A 2.C 3.C 4.C 5.B
二、6.CD
7.AD∥BC(或AD与BC平行)
8.平行 平行
9.∠EFG ∠BCD,∠AED DE∥BC 内错角相等,两直线平行 CD∥GF 同位角相等,两直线平行
10.内错角相等
三、11.解:∵∠3与∠1互余,∠3与∠2互余,
∴∠1=∠2.
∴AB∥CD.
12.①同位角∠A=∠CEF,∠B=∠EFC,
②内错角∠ADE=∠DEF,
③同旁内角.∠A+∠AEF=180°,∠B+∠BFE=180°,∠BDE+∠DEF=180°
思路点拨:AB,EF被AC所截,AB,EF被BC所截,AB,EF被DE所截,三个方面的关系中存在同位角,内错角,同旁内角来判定AB∥EF的条件.
13.解:CF∥AB.理由如下:
∵图中是一副直角三角板,
∴∠BAC=45°.
∵CF平分∠DCE,∠DCE=90°,
∴∠DCF=∠DCE=45°.
∴∠DCF=∠BAC.
∴CF∥AB.
14.解:∵∠A=∠C,∠B=∠D,
∴∠B+∠C=∠D+∠A
=360°÷2=180°.
∴AB∥CD.
∵∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D=360°÷2=180°.
∴AD∥BC.
15.解:∵EG⊥AB,∠E=30°,
∴∠AKF=∠EKG=60°=∠CHF,
∴AB∥CD.
16.DE∥BC. ∵∠1=∠3,∠1=∠2,∴∠2=∠3(等量代换)∴DE∥BC(内错角相等,两直线平行)。
17.提示:
这是一道结论开放的探究性问题,由于E点位置的不确定性,可引起对E点不同位置的分类讨论.本题可分为AB,CD之间或之外.
如:
结论:①∠AEC=∠A+∠C ②∠AEC+∠A+∠C=360°
③∠AEC=∠C-∠A ④∠AEC=∠A-∠C
⑤∠AEC=∠A-∠C ⑥∠AEC=∠C-∠A.
18.(1)∵AB⊥EF,CD⊥EF
∴AB∥CD(两条直线都垂直于同一条直线,这两条直线平行)
(2)延长NO′至P,可证∠EOM=∠EO′P=45°,得OM∥O′N.
解题技巧:(1)中由垂线定义及平行线判定推理来证,
(2)中要作辅助线延长NO′至P,运用同位角相等来证明.
21世纪教育网(www.21cnjy.com)
第五章 相交线与平行线
5.2.2 平行线的判定
一、选择题
1.如图所示,能说明AD∥BC,下列条件成立的是( )
A.∠2=∠3 B.∠1=∠4
C.∠1+∠2=∠3+∠4 D.∠A+∠C=180°
2.如图,工人师傅在工程施工中,需在同一平面内弯制一个变形管道ABCD,使其拐角∠ABC=150°,∠BCD=30°,则( )
A.AB∥BC B.BC∥CD
C.AB∥DC D.AB与CD相交
3.下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠5=180°,则a∥c
4.如图,用两个相同的三角板按照如图方式作平行线,能解释其中道理的定理是( )
A.同位角相等两直线平行 B.同旁内角互补,两直线平行
C.内错角相等两直线平行 D.平行于同一条直线的两直线平行
5.如图,下列条件中,不能判断直线 ∥ 的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
填空题
如图所示,若∠1=30°,∠2=80°,∠3=30°,∠4=70°,若AB∥____.
7.如图所示,已知∠1=∠2,则图中互相平行的线段是 .
8.如图,光线AB、CD被一个平面镜反射,此时∠1=∠3,∠2=∠4,那么AB和CD的位置关系是 ,BE和DF的位置关系是 .
(
B
A
C
D
E
F
1
2
3
4
)
9.看图填空:
如图,∠1的同位角是 , ∠1的内错角是 ,
如果∠1=∠BCD,那么 ,根据是 ;
如果∠ACD=∠EGF,那么 ,根据是 .
10.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线和,这是根据________________,两直线平行.
三、解答题
11.如图,∠3与∠1互余,∠3与∠2互余.试说明AB∥CD.
12.如图所示,写出所有角满足的条件使AB∥EF,并说明理由.
13.将一副直角三角尺拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F,试判断CF与AB是否平行,并说明理由.
14.如图,∠A+∠B+∠C+∠D=360°,且∠A=∠C,∠B=∠D,那么AB∥CD,AD∥BC.请说明理由.
15.如图所示,已知直线EF和AB,CD分别相交于K,H,且EG⊥AB,∠CHF=600,∠E=30°,试说明AB∥CD.
16.如图,∠1=∠3,∠1=∠2,那么DE与BC有怎样的位置关系?为什么?
17.如图,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A,∠AEC,∠C之间具有怎样的关系并说明理由.(提示:先画出示意图,再说明理由).
18.(1)如图(1)所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.
判断AB与CD的位置关系,并说明理由;
(2)如图(2)所示在(1)的条件下,若小路OM平分∠EOB.通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N位置关系.
参考答案:
一、1.A 2.C 3.C 4.C 5.B
二、6.CD
7.AD∥BC(或AD与BC平行)
8.平行 平行
9.∠EFG ∠BCD,∠AED DE∥BC 内错角相等,两直线平行 CD∥GF 同位角相等,两直线平行
10.内错角相等
三、11.解:∵∠3与∠1互余,∠3与∠2互余,
∴∠1=∠2.
∴AB∥CD.
12.①同位角∠A=∠CEF,∠B=∠EFC,
②内错角∠ADE=∠DEF,
③同旁内角.∠A+∠AEF=180°,∠B+∠BFE=180°,∠BDE+∠DEF=180°
思路点拨:AB,EF被AC所截,AB,EF被BC所截,AB,EF被DE所截,三个方面的关系中存在同位角,内错角,同旁内角来判定AB∥EF的条件.
13.解:CF∥AB.理由如下:
∵图中是一副直角三角板,
∴∠BAC=45°.
∵CF平分∠DCE,∠DCE=90°,
∴∠DCF=∠DCE=45°.
∴∠DCF=∠BAC.
∴CF∥AB.
14.解:∵∠A=∠C,∠B=∠D,
∴∠B+∠C=∠D+∠A
=360°÷2=180°.
∴AB∥CD.
∵∠A=∠C,∠B=∠D,
∴∠A+∠B=∠C+∠D=360°÷2=180°.
∴AD∥BC.
15.解:∵EG⊥AB,∠E=30°,
∴∠AKF=∠EKG=60°=∠CHF,
∴AB∥CD.
16.DE∥BC. ∵∠1=∠3,∠1=∠2,∴∠2=∠3(等量代换)∴DE∥BC(内错角相等,两直线平行)。
17.提示:
这是一道结论开放的探究性问题,由于E点位置的不确定性,可引起对E点不同位置的分类讨论.本题可分为AB,CD之间或之外.
如:
结论:①∠AEC=∠A+∠C ②∠AEC+∠A+∠C=360°
③∠AEC=∠C-∠A ④∠AEC=∠A-∠C
⑤∠AEC=∠A-∠C ⑥∠AEC=∠C-∠A.
18.(1)∵AB⊥EF,CD⊥EF
∴AB∥CD(两条直线都垂直于同一条直线,这两条直线平行)
(2)延长NO′至P,可证∠EOM=∠EO′P=45°,得OM∥O′N.
解题技巧:(1)中由垂线定义及平行线判定推理来证,
(2)中要作辅助线延长NO′至P,运用同位角相等来证明.
21世纪教育网(www.21cnjy.com)
