北师大版九年级下册2.5二次函数与一元二次方程 同步检测卷(word版含答案)
文档属性
| 名称 | 北师大版九年级下册2.5二次函数与一元二次方程 同步检测卷(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 218.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览


文档简介
北师大版同步检测卷:二次函数与一元二次方程
一、选择题(共10小题;共50分)
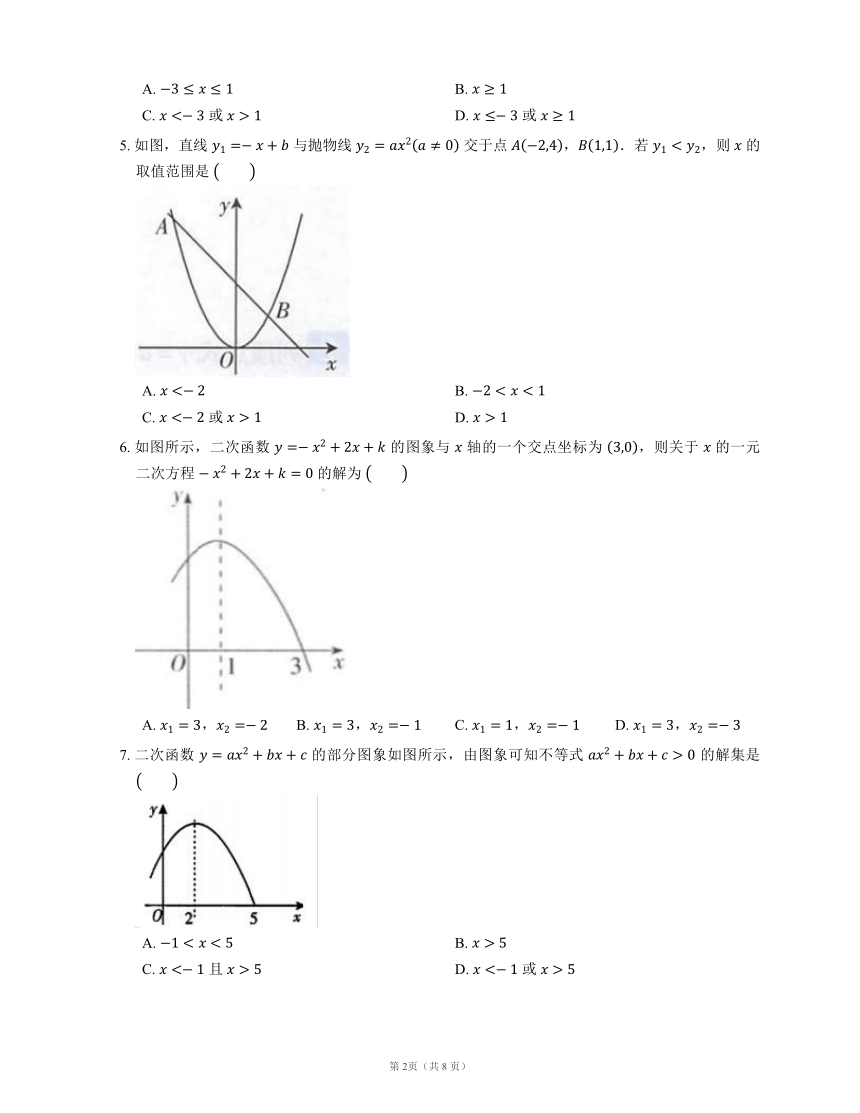
1. 二次函数 的图象如图所示,则方程 的根是
A. , B. , C. , D. ,
2. 如图,二次函数 的图象与 轴相交于 和 两点,当函数值 时,自变量 的取值范围是
A. B.
C. D. 或
3. 二次函数 的图象与 轴的交点个数
A. 有 个 B. 有 个 C. 有 个 D. 无法判断
4. 如图所示是二次函数 的图象,若 ,则 的取值范围是
A. B.
C. 或 D. 或
5. 如图,直线 与抛物线 交于点 ,.若 ,则 的取值范围是
A. B.
C. 或 D.
6. 如图所示,二次函数 的图象与 轴的一个交点坐标为 ,则关于 的一元二次方程 的解为
A. , B. , C. , D. ,
7. 二次函数 的部分图象如图所示,由图象可知不等式 的解集是
A. B.
C. 且 D. 或
8. 在平面直角坐标系中,已知 ,设函数 的图象与 轴有 个交点,函数 的图象与 轴有 个交点,则
A. 或 B. 或
C. 或 D. 或
9. 已知二次函数 ( 为常数)的图象与 轴有交点,且当 时, 随 的增大而增大,则 的取值范围是
A. B. C. D.
10. 如图,在平面直角坐标系中,直线 与抛物线 交于 , 两点,则关于 的不等式 的解集是
A. B.
C. D. 或
二、填空题(共5小题;共25分)
11. 如图,抛物线 与直线 的两个交点坐标分别为 ,,则关于 的方程 的解为 .
12. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
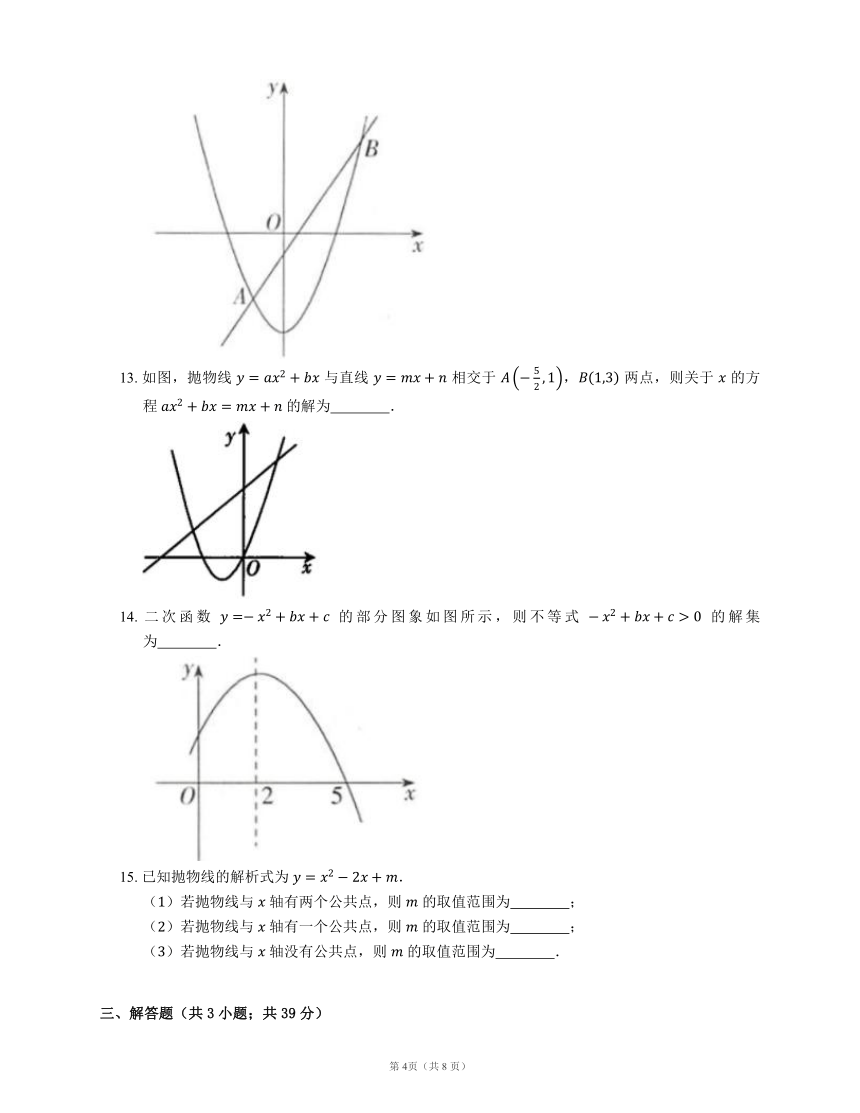
13. 如图,抛物线 与直线 相交于 , 两点,则关于 的方程 的解为 .
14. 二次函数 的部分图象如图所示,则不等式 的解集为 .
15. 已知抛物线的解析式为 .
()若抛物线与 轴有两个公共点,则 的取值范围为 ;
()若抛物线与 轴有一个公共点,则 的取值范围为 ;
()若抛物线与 轴没有公共点,则 的取值范围为 .
三、解答题(共3小题;共39分)
16. 已知抛物线 .
(1)求证:无论 为何值,该抛物线与 轴总有两个交点;
(2)该抛物线与 轴交于 , 两点,点 在点 的左侧,且 ,求 的值.
17. 在平面直角坐标系 (如图)中,二次函数 (其中 是常数,且 )的图象是开口向上的抛物线.
(1)求该抛物线的顶点 的坐标;
(2)我们将横、纵坐标都是整数的点叫做“整点”,将抛物线 与 轴的交点记为 ,如果线段 上的“整点”的个数小于 ,试求 的取值范围;
(3)如果 ,,, 这四个函数值中有且只有一个值大于 ,试写出符合题意的一个函数解析式;结合函数图象,求 的取值范围.
18. 已知函数 ( 是常数).
(1)当 时,该函数图象与直线 有几个公共点
(2)若函数图象与 轴只有一个公共点,求 的值.
答案
第一部分
1. C 【解析】由题图得抛物线与 轴的交点坐标为 ,,
所以方程 的根为 ,.
2. D
3. C
4. A
5. C
6. B 【解析】因为二次函数 的图象与 轴的一个交点坐标为 ,
所以 是方程 的一个根,由题图得,二次函数 的图象的对称轴为直线 ,
所以方程 的另一个根为 .
7. A
8. C 【解析】,,
函数 的图象与 轴有 个交点,即 ,
函数 ,
当 时,,
函数 的图象与 轴有 个交点,即 ,此时 ;
当 时,不妨令 ,
,
,函数 为一次函数,与 轴有一个交点,即 ,此时 .
综上可知, 或 .
故选C.
9. D 【解析】 二次函数 ( 为常数)的图象与 轴有交点,
,解得 .
抛物线的对称轴为直线 ,
抛物线开口向上,且当 时, 随 的增大而增大,
,
实数 的取值范围是 .
10. D
【解析】观察题图可知,当 或 时,直线 在拋物线 的上方,
不等式 的解集为 或 .
第二部分
11. ,
12.
【解析】抛物线 与直线 交于 , 两点,观察图象可知:当 时,直线 在抛物线 的上方,
不等式 的解集为 ,即不等式 的解集是 .
13. ,
14.
【解析】抛物线的对称轴为直线 ,而抛物线与 轴的一个交点坐标为 ,
所以抛物线与 轴的另一个交点坐标为 ,
当 时,抛物线在 轴上方,
所以不等式 的解集为 .
15. ,,
第三部分
16. (1) ,
无论 为何值时,该抛物线与 轴总有两个交点
(2) 令 ,得 .
解得 ,.
,点 在点 的左侧,
.解得 或 ,即 的值为 或 .
17. (1) 抛物线的方程为 ,
抛物线的顶点坐标为 ;
(2) 为抛物线与 轴的交点,
点坐标为 ,
线段 上的整点个数小于 ,
则可知 ,,
故 的取值范围为 ;
(3) 已知 ,,, 有且只有一个大于 ,(即其余的小于或等于 )
由题可知该函数对称轴为 ,开口方向向上,
故有 ,
,
得 ,
得 ,
,
得 ,
得 ,
取 ,
,
的取值范围为 .
18. (1) 当 时,.
令 .化简,得 .
.
方程有两个不相等的实数根.
函数 的图象与直线 有两个不同的公共点.
(2) ①当 时,函数 的图象与 轴只有一个公共点 .
②当 时,若函数 的图象与 轴只有一个公共点,则方程 有两个相等的实数根.
.
.
综上所述, 的值为 或 .
第1页(共1 页)
一、选择题(共10小题;共50分)
1. 二次函数 的图象如图所示,则方程 的根是
A. , B. , C. , D. ,
2. 如图,二次函数 的图象与 轴相交于 和 两点,当函数值 时,自变量 的取值范围是
A. B.
C. D. 或
3. 二次函数 的图象与 轴的交点个数
A. 有 个 B. 有 个 C. 有 个 D. 无法判断
4. 如图所示是二次函数 的图象,若 ,则 的取值范围是
A. B.
C. 或 D. 或
5. 如图,直线 与抛物线 交于点 ,.若 ,则 的取值范围是
A. B.
C. 或 D.
6. 如图所示,二次函数 的图象与 轴的一个交点坐标为 ,则关于 的一元二次方程 的解为
A. , B. , C. , D. ,
7. 二次函数 的部分图象如图所示,由图象可知不等式 的解集是
A. B.
C. 且 D. 或
8. 在平面直角坐标系中,已知 ,设函数 的图象与 轴有 个交点,函数 的图象与 轴有 个交点,则
A. 或 B. 或
C. 或 D. 或
9. 已知二次函数 ( 为常数)的图象与 轴有交点,且当 时, 随 的增大而增大,则 的取值范围是
A. B. C. D.
10. 如图,在平面直角坐标系中,直线 与抛物线 交于 , 两点,则关于 的不等式 的解集是
A. B.
C. D. 或
二、填空题(共5小题;共25分)
11. 如图,抛物线 与直线 的两个交点坐标分别为 ,,则关于 的方程 的解为 .
12. 如图,抛物线 与直线 交于 , 两点,则不等式 的解集是 .
13. 如图,抛物线 与直线 相交于 , 两点,则关于 的方程 的解为 .
14. 二次函数 的部分图象如图所示,则不等式 的解集为 .
15. 已知抛物线的解析式为 .
()若抛物线与 轴有两个公共点,则 的取值范围为 ;
()若抛物线与 轴有一个公共点,则 的取值范围为 ;
()若抛物线与 轴没有公共点,则 的取值范围为 .
三、解答题(共3小题;共39分)
16. 已知抛物线 .
(1)求证:无论 为何值,该抛物线与 轴总有两个交点;
(2)该抛物线与 轴交于 , 两点,点 在点 的左侧,且 ,求 的值.
17. 在平面直角坐标系 (如图)中,二次函数 (其中 是常数,且 )的图象是开口向上的抛物线.
(1)求该抛物线的顶点 的坐标;
(2)我们将横、纵坐标都是整数的点叫做“整点”,将抛物线 与 轴的交点记为 ,如果线段 上的“整点”的个数小于 ,试求 的取值范围;
(3)如果 ,,, 这四个函数值中有且只有一个值大于 ,试写出符合题意的一个函数解析式;结合函数图象,求 的取值范围.
18. 已知函数 ( 是常数).
(1)当 时,该函数图象与直线 有几个公共点
(2)若函数图象与 轴只有一个公共点,求 的值.
答案
第一部分
1. C 【解析】由题图得抛物线与 轴的交点坐标为 ,,
所以方程 的根为 ,.
2. D
3. C
4. A
5. C
6. B 【解析】因为二次函数 的图象与 轴的一个交点坐标为 ,
所以 是方程 的一个根,由题图得,二次函数 的图象的对称轴为直线 ,
所以方程 的另一个根为 .
7. A
8. C 【解析】,,
函数 的图象与 轴有 个交点,即 ,
函数 ,
当 时,,
函数 的图象与 轴有 个交点,即 ,此时 ;
当 时,不妨令 ,
,
,函数 为一次函数,与 轴有一个交点,即 ,此时 .
综上可知, 或 .
故选C.
9. D 【解析】 二次函数 ( 为常数)的图象与 轴有交点,
,解得 .
抛物线的对称轴为直线 ,
抛物线开口向上,且当 时, 随 的增大而增大,
,
实数 的取值范围是 .
10. D
【解析】观察题图可知,当 或 时,直线 在拋物线 的上方,
不等式 的解集为 或 .
第二部分
11. ,
12.
【解析】抛物线 与直线 交于 , 两点,观察图象可知:当 时,直线 在抛物线 的上方,
不等式 的解集为 ,即不等式 的解集是 .
13. ,
14.
【解析】抛物线的对称轴为直线 ,而抛物线与 轴的一个交点坐标为 ,
所以抛物线与 轴的另一个交点坐标为 ,
当 时,抛物线在 轴上方,
所以不等式 的解集为 .
15. ,,
第三部分
16. (1) ,
无论 为何值时,该抛物线与 轴总有两个交点
(2) 令 ,得 .
解得 ,.
,点 在点 的左侧,
.解得 或 ,即 的值为 或 .
17. (1) 抛物线的方程为 ,
抛物线的顶点坐标为 ;
(2) 为抛物线与 轴的交点,
点坐标为 ,
线段 上的整点个数小于 ,
则可知 ,,
故 的取值范围为 ;
(3) 已知 ,,, 有且只有一个大于 ,(即其余的小于或等于 )
由题可知该函数对称轴为 ,开口方向向上,
故有 ,
,
得 ,
得 ,
,
得 ,
得 ,
取 ,
,
的取值范围为 .
18. (1) 当 时,.
令 .化简,得 .
.
方程有两个不相等的实数根.
函数 的图象与直线 有两个不同的公共点.
(2) ①当 时,函数 的图象与 轴只有一个公共点 .
②当 时,若函数 的图象与 轴只有一个公共点,则方程 有两个相等的实数根.
.
.
综上所述, 的值为 或 .
第1页(共1 页)
