安徽省滁州市定远县育才学校2021-2022学年九年级上学期第三次月考数学试题(PDF版含答案解析)
文档属性
| 名称 | 安徽省滁州市定远县育才学校2021-2022学年九年级上学期第三次月考数学试题(PDF版含答案解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 680.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览


文档简介
育才学校 2021-2022 学年度第一学期第三次月考卷
九年级数学
一、选择题(本大题共 10 小题,每小题 4 分,满分 40 分)
1.已知关于 x 的方程 x2 3x a 0有一个根为-2,则 a 的值为( )
A.5 B.2 C.-2 D.-5
k
2.已知反比例函数 y 的图象经过点 (3,2),小良说了四句话,其中正确的是( )
x
A.当 x 0时, y 0 B.函数的图象只在第一象限
C. y随 x的增大而增大 D.点 ( 3,2)不在此函数的图象上
3.如图,在 ABC中,DE∥AC,BD=6cm,DA=3cm,BE=4cm,则 EC的长为( )
A.1cm B.2cm C.3cm D.4cm
4.如图,有一块边长为 6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的
虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
2 3 3 2 9 3 2 27A. 3 cm B. cm C. cm D. 32 cm
2
2 2
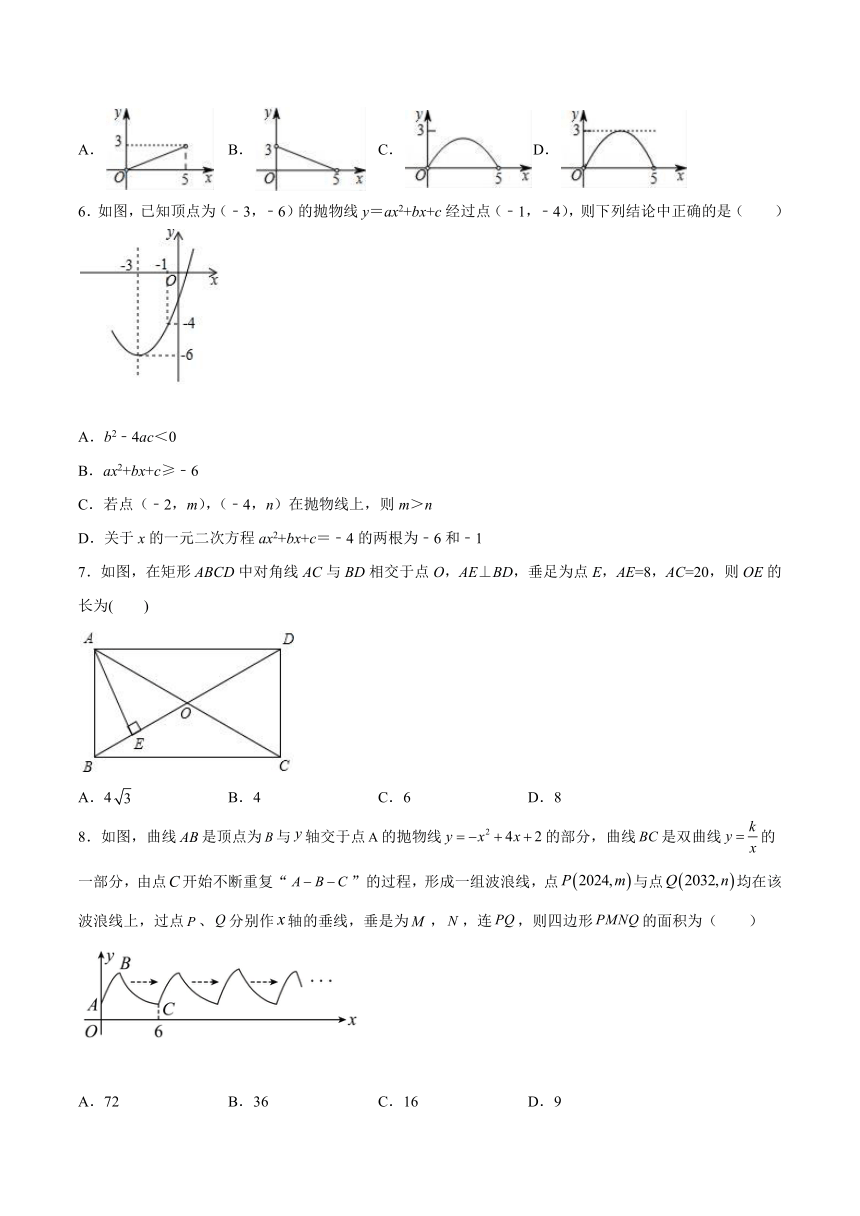
5.如图,矩形 ABCD中,AB=3,BC=5,点 P是 BC边上的一个动点(点 P不与点 B,C重合),现将△PCD
沿直线 PD折叠,使点 C落下点 C1处;作∠BPC1的平分线交 AB于点 E.设 BP=x,BE=y,那么 y关于 x
的函数图象大致应为( )
A. B. C. D.
6.如图,已知顶点为(﹣3,﹣6)的抛物线 y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中正确的是( )
A.b2﹣4ac<0
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣4,n)在抛物线上,则 m>n
D.关于 x的一元二次方程 ax2+bx+c=﹣4的两根为﹣6和﹣1
7.如图,在矩形 ABCD中对角线 AC与 BD相交于点 O,AE⊥BD,垂足为点 E,AE=8,AC=20,则 OE的
长为( )
A.4 3 B.4 C.6 D.8
k
8.如图,曲线 AB是顶点为 B与 y轴交于点A的抛物线 y x2 4x 2的部分,曲线 BC是双曲线 y 的
x
一部分,由点C开始不断重复“ A B C”的过程,形成一组波浪线,点 P 2024,m 与点Q 2032,n 均在该
波浪线上,过点 P、Q分别作 x轴的垂线,垂是为M ,N ,连 PQ,则四边形 PMNQ的面积为( )
A.72 B.36 C.16 D.9
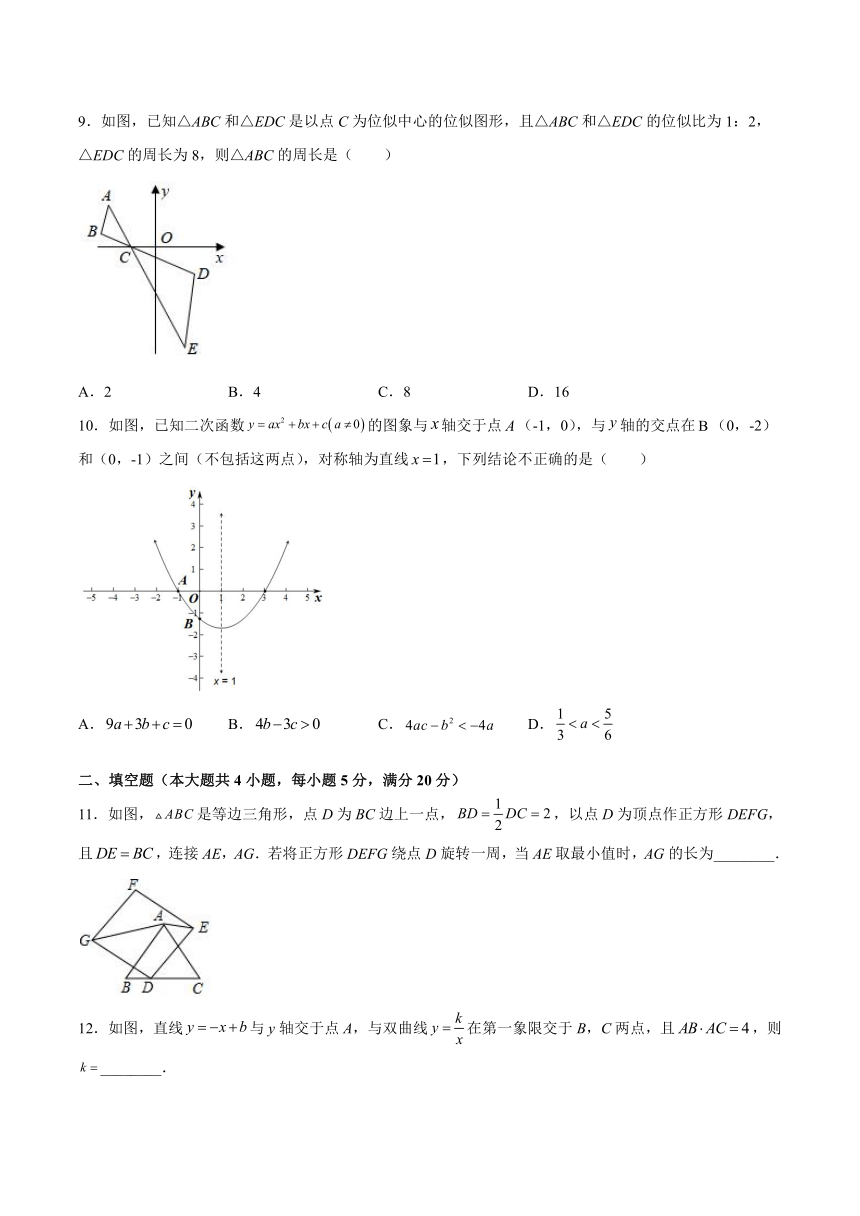
9.如图,已知△ABC和△EDC是以点 C为位似中心的位似图形,且△ABC和△EDC的位似比为 1:2,
△EDC的周长为 8,则△ABC的周长是( )
A.2 B.4 C.8 D.16
10.如图,已知二次函数 y ax2 bx c a 0 的图象与 x轴交于点 A(-1,0),与 y轴的交点在B(0,-2)
和(0,-1)之间(不包括这两点),对称轴为直线 x 1,下列结论不正确的是( )
A.9a 3b c 0 B.4b 3c 0 C. 4ac b2
1 5
4a D. a
3 6
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
1
11.如图, ABC是等边三角形,点 D为 BC边上一点, BD DC 2,以点 D为顶点作正方形 DEFG,
2
且DE BC,连接 AE,AG.若将正方形 DEFG绕点 D旋转一周,当 AE取最小值时,AG的长为________.
12.如图,直线 y x b
k
与 y轴交于点 A,与双曲线 y 在第一象限交于 B,C两点,且 AB AC 4,则
x
k ________.
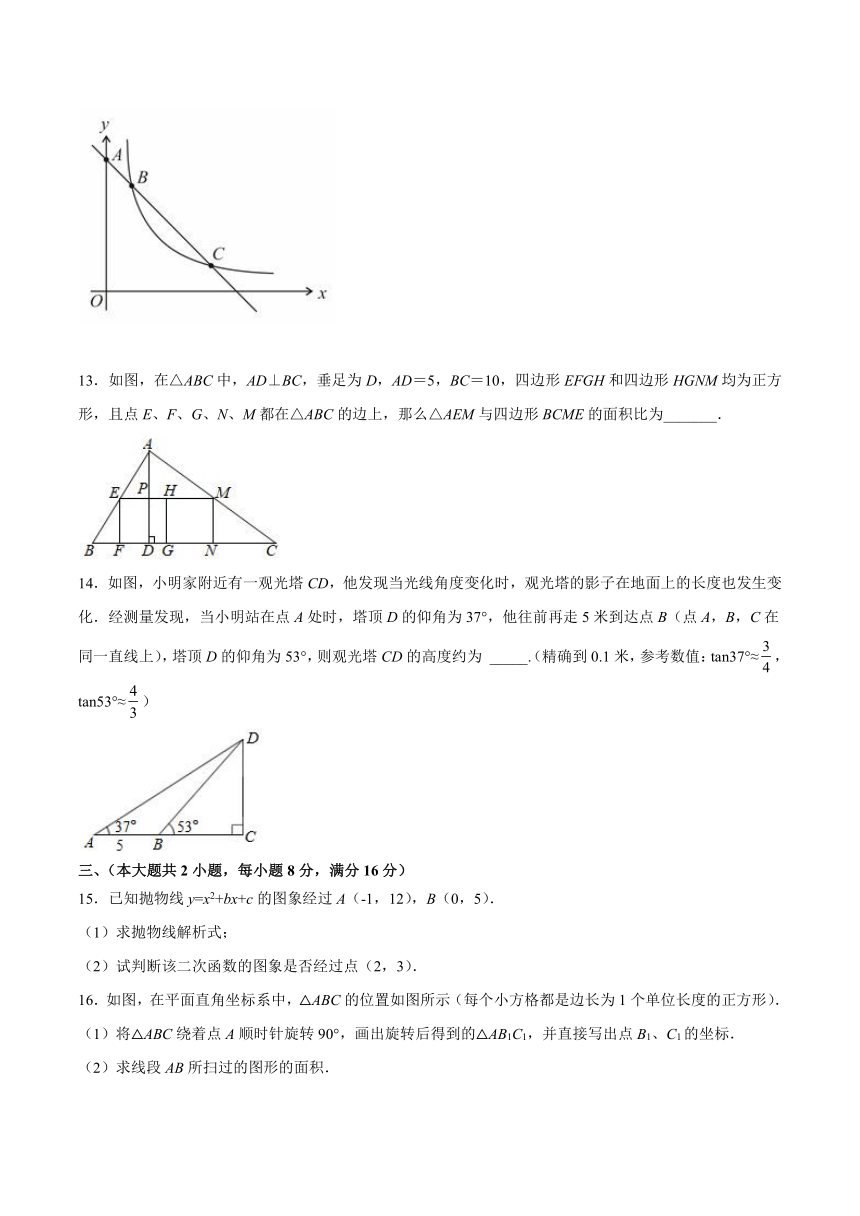
13.如图,在△ABC中,AD⊥BC,垂足为 D,AD=5,BC=10,四边形 EFGH和四边形 HGNM均为正方
形,且点 E、F、G、N、M都在△ABC的边上,那么△AEM与四边形 BCME的面积比为_______.
14.如图,小明家附近有一观光塔 CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变
化.经测量发现,当小明站在点 A处时,塔顶 D的仰角为 37°,他往前再走 5米到达点 B(点 A,B,C在
3
同一直线上),塔顶 D的仰角为 53°,则观光塔 CD的高度约为 _____(. 精确到 0.1米,参考数值:tan37°≈ ,
4
4
tan53°≈ )
3
三、(本大题共 2 小题,每小题 8 分,满分 16 分)
15.已知抛物线 y=x2+bx+c的图象经过 A(-1,12),B(0,5).
(1)求抛物线解析式;
(2)试判断该二次函数的图象是否经过点(2,3).
16.如图,在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为 1个单位长度的正方形).
(1)将△ABC绕着点 A顺时针旋转 90°,画出旋转后得到的△AB1C1,并直接写出点 B1、C1的坐标.
(2)求线段 AB所扫过的图形的面积.
四、(本大题共 2 小题,每小题 6 分,满分 12 分)
17.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销 x件.已知产销两种产品的有关信息
如表:
其中 a为常数,且 5≤a≤7.
(1)若产销甲、乙两种产品的年利润分别为 y1万元、 y2万元,直.接.写出 y1、 y2与 x的函数关系式;(注:
年利润=总售价﹣总成本﹣每年其他费用)
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
18.已知二次函数 y=x2﹣4x+3.
(1)用配方法求出顶点坐标;
(2)求该二次函数与坐标轴的交点坐标;
(3)在所给坐标系中画出该二次函数的大致图象,并写出当 y<0时,x的取值范围.
五、(本大题共 1 小题,满分 12 分)
19.通过计算几何图形的面积可以解释代数恒等式的正确性,同样利用几何图形的面积也可以解释不等式
的正确性,请解答下列问题:
(1)根据图①,写出一个代数恒等式,得
(2)两个边长为 a、 b、 c的直角三角形和一个两条直角边均为 c的直角三角形拼成图②,请根据图②中图
形面积的关系写出一个代数恒等式,并写出推导过程;
(3)已知 a、 b、c、a'、b'、 c'均为正数,且满足 a a ' b b ' c c ' m,请画出一个图形,然后利用
该图形面积关系说明 ab ' a 'c bc ' m 2
六、(本大题共 1 小题,满分 14 分)
20.如图,已知抛物线 y ax2 bx 3经过点 A 1,0 和点 B 3,0 ,点 C为抛物线与 y轴的交点.
1 求抛物线的解析式;
2 若点 E为直线 BC上方抛物线上的一点,请求出 BCE面积的最大值.
3 在 2 条件下,是否存在这样的点D 0,m ,使得 BDE为等腰三角形?如果有,请直接写出点 D的坐标;
如果没有,请说明理由.
七、(本大题共 1 小题,满分 8 分)
21.如图,在 ABC中,点D, E,F分别在 AB, BC, AC 边上,DE / /AC,EF / /AB.
(1)求证: BDE∽△EFC.
AF 1
(2)设 ,
FC 2
①若 BC 12,求线段 BE的长;
②若△EFC的面积是 20,求 ABC的面积.
八、(本大题共 1 小题,满分 12 分)
m
22.如图,在平面直角坐标系中,一次函数 y1=kx+b(k≠0)的图象与反比例函数 y2= (m≠0)的图象x
相交于第一、三象限内的 A(3,5),B(a,﹣3)两点,与 x轴交于点 C.
(1)求该反比例函数和一次函数的解析式;
(2)在 y轴上找一点 P使 PB﹣PC最大,求 PB﹣PC的最大值及点 P的坐标;
m
(3)直接写出不等式 kx+b> 的解集.
x
八、(本大题共 1 小题,满分 16 分)
23.如图,在△ABC中,AB=AC=10,BC=16,点 D为 BC边上的动点(点 D不与点 B、C重合). 以点 D
为顶点作∠ADE=∠B,射线 DE交 AC边于点 E,过点 A作 AF⊥AD交射线 DE于点 F,连接 CF.
(1)求证:△ABD∽△DCE;
AD
(2)探索:点 D在 BC边上运动的过程中, 的值是否发生变化?若变化,请说明理由;若不变化,请
DF
求出其值;
(3)当△ABD为等腰三角形时,线段 EF的长为__________.
参考答案
1.B
【解析】根据题意,将 x=-2代入方程 x2+3x+a=0,得:4-6+a=0,
解得:a=2,故选:B.
2.D
k
解:∵反比例函数 y 的图象经过点(3,2),
x
∴k=2×3=6,
y 6∴ ,
x
∴图象在一、三象限,在每个象限 y随 x的增大而减小,故 A,B,C错误,
∴点 ( 3,2)不在此函数的图象上,选项 D正确;
故选:D.
3.B
解:∵DE∥AC,
∴BD:DA=BE:EC,即 6:3=4:EC,
解得:EC=2(cm).故选:B.
4.C
试题解析:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形 ADOK≌筝形 BEPF≌筝形 AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形 ODEP、四边形 PFGQ、四边形 QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结 AO,
在 Rt△AOD和 Rt△AOK中,
AO AO
{
OD OK,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设 OD=x,则 AO=2x,由勾股定理就可以求出 AD= 3 x,
∴DE=6-2 3 x,
∴纸盒侧面积=3x(6-2 3 x)=-6 3 x2+18x,
=-6 3 3 9 3(x- )2+ ,
2 2
∴当 x= 3 9 3时,纸盒侧面积最大为 .
2 2
故选 C.
考点:1.二次函数的应用;2.展开图折叠成几何体;3.等边三角形的性质.
5.C
【详解】由翻折的性质得,∠CPD=∠C′PD,
∵PE平分∠BPC1,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=90°,
∵∠C=90°,
∴∠CPD+∠PDC=90°,
∴∠BPE=∠PDC,
又∵∠B=∠C=90°,
∴△PCD∽△EBP,
BE PB
∴ ,
PC CD
y x
即 ,
5 x 3
1 1 5 25
∴y= x(5﹣x)=﹣ (x﹣ )2+ ,
3 3 2 12
∴函数图象为 C选项图象.
故选 C.
6.B
【详解】A、图象与 x轴有两个交点,方程 ax2+bx+c=0有两个不相等的实数根,b2﹣4ac>0,
所以 b2>4ac,故 A选项不符合题意;
B、抛物线的开口向上,函数有最小值,因为抛物线的最小值为﹣6,所以 ax2+bx+c≥﹣6,
故 B选项符合题意;
C、抛物线的对称轴为直线 x=﹣3,因为﹣4离对称轴的距离等于﹣2离对称轴的距离,所以
m=n,故 C选项不符合题意;
D、根据抛物线的对称性可知,(﹣1,﹣4)关于对称轴的对称点为(﹣5,﹣4),所以关于
x的一元二次方程 ax2+bx+c=﹣4的两根为﹣5和﹣1,故 D选项不符合题意.
故选 B.
7.C
解:∵四边形 ABCD是矩形,
1
∴AO=CO AC=10,
2
∴OE AO2 AE2 100 64 6.
故选:C.
8.B
【详解】
如图,过点 B作 x轴的垂线交于M ,取 DE的中点Q ,过点Q 作 x轴的垂线交于 N ,
y x2 4x 2 (x 2)2 6,
B(2,6),
把 B(2, 6)
k
代入 y 中得: k 12,
x
12反比例函数解析式为 y ,
x
由图可知,每经过 6为一次循环,
2024 6 337 2, 2032 6 338 4,
点 P离 x轴的距离与点 B离 x轴的距离相同,点 Q离 x轴距离与点Q 离 x轴距离相同,
12
令 x 4代入 y 中得: y 3,
x
Q N 3, BM 6,M N 2032 2024 8,
S 1PMNQ S BM N Q (6 3) 8 36四边形 四边形 .2
故选:B.
9.B
【详解】∵△ABC和△EDC的位似比为 1:2,
∴△ABC和△EDC的相似比为 1:2,
又∵△EDC的周长为 8,
C△ABC C △ABC 1∴ C ,△EDC 8 2
∴△ABC的周长为 4.故选 B.
10.D
【详解】∵ A(-1,0),对称轴为 x 1
∴二次函数与 x 轴的另一个交点为 3,0
将 3,0 2代入 y ax bx c a 0 中
0 9a 3b c,故 A正确
2
将 1,0 , 3,0 代入 y ax bx c a 0 中
0 a b c①
0 9a 3b c②
② 9 ①
0 12b 8c
2c 3b
4b 8 1∴ 3c c 3c c
3 3
∵二次函数与 y轴的交点在B(0,-2)和(0,-1)之间(不包括这两点)
∴ 2 c 1
∴4b 3c
1
c 0
3
∴4b 3c 0,故 B正确;
∵二次函数与 y轴的交点在B(0,-2)和(0,-1)之间(不包括这两点)
4ac b2
∴抛物线顶点纵坐标 1
4a
∵抛物线开口向上
∴ a 0
∴ 4ac b2 4a,故 C正确
∵二次函数与 y轴的交点在B(0,-2)和(0,-1)之间(不包括这两点)
∴ 2 c 1
将 1,0 , 3,0 代入 y ax2 bx c a 0 中
0 a b c①
0 9a 3b c②
① 3 ②
0 12a 4c
c 3a
∴ 2 3a 1
1 a 2∴ ,故 D错误,符合题意
3 3
故答案为:D.
11.8
【详解】过点 A作 AM BC 于 M,
BD 1∵ DC 2,
2
∴DC 4,
∴ BC BD DC 2 4 6,
∵ ABC是等边三角形,
∴ AB AC BC 6,
∵ AM BC ,
BM 1 BC 1∴ 6 3,
2 2
∴DM BM BD 3 2 1,
在RtVABM 中, AM AB2 BM 2 62 32 3 3,
当正方形 DEFG绕点 D旋转到点 E、A、D在同一条直线上时, AD AE DE,
即此时 AE取最小值,
在RtVADM 中, AD DM 2 AM 2 12 (3 3)2 2 7,
∴在RtVADG中, AG AD2 DG2 (2 7)2 62 8;
故答案为 8.
12.2
解:如图所示,过点 B作 BE⊥AO于 E,过点 C作 CF⊥AO于 F,设直线 y x b与 x轴
的交点为 G,
∵A、G分别是直线 y x b与 y轴,x轴的交点,
∴A点坐标为(0,b),G点坐标为(b,0),
∴OA=OG,
∴∠OAG=∠OGA=45°,
∴∠ABE=45°,
∴AE=BE,
∴ AB 2BE,
同理可得 AC 2CF,
设 B点坐标为(m,-m+b),C点坐标为(n,-n+b),
y x b
联立 k 得 x2y bx k 0
,
x
∴mn k,
∵ AB AC 4,
∴ 2m 2n 4,即 2k 4,
∴ k 2.
13.1:3
【详解】
∵四边形 EFGH和四边形 HGNM均为正方形,AD⊥BC,
∴四边形 EFDP是矩形, AP EM ,
∴PD EF EH HM ,
∴设 PD EF EH HM x,
∴ EM 2x, AP 5 x,
∵ EM∥BC,
∴ AEM B, AME C,
∴ AEM∽ ABC,
∵AP和 AD分别是 AEM 和 ABC的高,
AP EM 5 x 2x
∴ ,代入得: ,
AD BC 5 10
x 5 5解得: ,即 PD ,
2 2
∴ AP 5
5 5
,
2 2
5
∴ AP 2 1 ,
AD 5 2
S AEM AP 2 1 2 1
∴ ( ) ( ) S , ABC AD 2 4
∵ S ABC S AEM S四边形BCME,
∴ S AEM : S BCME 1:3四边形 .
故答案为:1:3.
14.8.6米
解:由题意知,∠A=37°,∠DBC=53°,∠D=90°,AB=5,
CD
在 Rt△CBD中,tan∠DBC= ,
BC
CD 3
∴BC= ≈ CD,
tan 53 4
CD CD 3
在 Rt△CAD中,tan∠A= ,即 3
AC 5 CD
=tan37°≈
4 4
60
∴解得:CD= ≈8.6,
7
答:观光塔 CD的高度约为 8.6米.
15.(1) y x2 6x 5;(2)该二次函数的图像不经过点(2,3)
解:(1)抛物线 y x2 bx c的图像经过 A(-1,12),B(0,5).
1 b c 12 b 6
∴ c 5 ,解得: , c 5
二次函数解析式为: y x2 6x 5;
(2)当 x=2时,y=x2-6x+5=4-12+5=-3,
∴该二次函数的图象不经过点(2,3).
16.
【详解】(1)如图所示,△AB1C1即为所求;
由图可知点 B1的坐标为(4,﹣2)、C1的坐标为(1,﹣3);
(2)∵AB= 32 32 =3 2,且∠BAB1=90°,
2
AB 90 3 2
9
∴线段 所扫过的图形的面积为 = π.
360 2
17.【解析】
(1) 解:(1)y1=(8-a)x-20,(0<x≤200)
y 10x 30 0.05x22 = 0.05x2 10x 30.(0<x≤90).
(2)对于 y1=(8-a)x-20.
∵8-a>0,∴x=200时,y1的值最大=(1580-200a)万元.
对于 y2 0.05 x 100
2 470.
∵0<x≤90,∴x=90时, y2最大值=465万元.
(3)①(1580-200a)=465,解得 a=5.575,②(1580-200a)>465,解得 a<5.575,③(1580-200a)
<465,解得 a>5.575.
∵5≤a≤7,∴当 a=5.575时,生产甲乙两种产品的利润相同.
当 5≤a<5.575时,生产甲产品利润比较高.
当 5.575<a≤7时,生产乙产品利润比较高.
18.(1)顶点坐标为(2,-1);(2)该二次函数与 x轴的交点坐标为(1,0)(3,0);(3)
当 y<0时,1<x<3.
解:(1)因为 y=x2-4x+3=x2-4x+4-1=(x-2)2-1,
所以抛物线的顶点坐标为(2,-1);
(2)当 y=0时,x2-4x+3=0,解得 x1=1,x2=3,
所以该二次函数与 x轴的交点坐标为(1,0)(3,0);
(2)当 x=0时,y=3,当 x=4时,y= 42-4 4+3=3,
描点,连线,函数图象如图:
由图象可知,当 y<0时,1<x<3.
19.(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;(2)过程见详解;(3)过程见详解
解:(1)由图①可得:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)a2+b2=c2,证明如下:
1
梯形的面积为: 2 (a+b)(a+b
1 1
)= 2 ab×2+
2
2 c ,
化简即可得:a2+b2=c2;
(3)构造一个边长为 m的正方形,如图所示:
显然 a a ' b b ' c c ' m,
根据图形可知,正方形内部 3个矩形的面积和小于正方形的面积,
ab ' a 'c bc ' m2.
20.(1) y x2 2x 3.(2)当 n
3
时, BCE 27面积取最大值,最大值为 .(3)点 D
2 8
的坐标为 0,0 、 0,
15
、 0,
39
、 0,
3 13 3 13
或 0,
2 40 4 4
详解: 1 将 A 1,0 、B 3,0 代入 y ax2 bx 3,
a b 3 0 a 1得: 9a 3b 3 0,解得: b 2,
抛物线的解析式为 y x2 2x 3.
2 过点 E作 EF / / y轴,交 BC于点 F,如图 1所示.
当 x 0时, y x2 2x 3 3,
点 C的坐标为 0,3 .
设直线 BC的解析式为 y kx c,
将B 3,0 、C 0,3 代入 y kx c,得:
3k b 0 k 1b 3,解得: b 3,
直线 BC的解析式为 y x 3.
2
设点 E的坐标为 n, n 2n 3 ,则点 F的坐标为 n, n 3 ,
EF n2 2n 3 n 3 n2 3n,
S 1 3 2 9 3 3 2 27 BCE EF OB n n (n ) ,2 2 2 2 2 8
n 3 BCE 27当 时, 面积取最大值,最大值为 .
2 8
3 2 3由 可知点 E的坐标为 ,
15
2 4
.
BDE为等腰三角形分三种情况 (如图 2):
3
①当 ED EB时,有 ( )2 (
15
m)2 (3 3)2 (15)2 ,
2 4 2 4
解得:m 0 m
15
1 , 2 ,2
15
点 D的坐标为 0,0 或 0, 2 ;
② DE DB (3 0)2 2
3 15
当 时,有 (0 m) ( 0)2 ( m)2,
2 4
39
解得:m3 ,40
39 点 D的坐标为 0, ;
40
2 2 3 15③当 BD BE时,有 (3 0) (0 m) ( 3)2 ( )2,
2 4
m 3 13 m 3 13解得: 4 , 5 ,4 4
点 D的坐标为 0,
3 13 0, 3 13
4
或 4
.
0,0 0,15 0, 39
0, 3 13
3 13
综上所述:当点 D的坐标为 、 2 、 、 或
0, 时,
40 4
BDE
4
为等腰三角形.
21.
( 1)证明:∵DE∥AC,
∴∠BED=∠C,
又∵EF∥AB,
∴∠B=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
BE AF 1
∴ ,
EC FC 2
∵BC=12,
BE 1
∴ ,
12 BE 2
∴BE=4;
AF 1
②∵ ,
FC 2
CF 2
∴ ,
AC 3
∵EF∥AB,
∴∠CEF=∠B,
∵∠C=∠C.
∴△EFC∽△BAC,
S EFC CF 2 4
∴ ( ) S , ABC AC 9
∵S△EFC=20,
4
∴S△ABC=20÷ =45.9
15
22.(1)y1=x+2,y2= ;(2)最大值3 2,P(0,2);(3)﹣5<x<0或 x>3x
m
解:(1)把 A(3,5)代入 y2= (m≠0),可得 m=3×5=15,x
15
∴反比例函数的解析式为 y2= ,x
把点 B(a,﹣3)代入,可得 a=﹣5,
∴B(﹣5,﹣3).
把 A(3,5),B(﹣5,﹣3)代入 y1=kx+b,
3k+b=5
可得 ,
5k+b=3
k=1
解得 ,
b=2
∴一次函数的解析式为 y1=x+2;
(2)一次函数的解析式为 y1=x+2,令 x=0,则 y=2,
∴一次函数与 y轴的交点为 P(0,2),
此时,PB﹣PC=BC最大,P即为所求,
令 y=0,则 x=﹣2,
∴C(﹣2,0),
过 B点向 x轴作垂线,由勾股定理可得:
BC 5 2 2 32 3 2;
(3)∵A(3,5),B(﹣5,﹣3)
∴根据函数图象可知,当 y1>y2时,﹣5<x<0或 x>3.
m
即 kx+b> 的解集为:﹣5<x<0或 x>3.
x
AD AD 4 25 55 13
23.(1)见解析;(2) 的值不发生变化, 的值为 ;(3) 或 或 10
DF DF 5 2 32 10
(1)证明: AB AC
ABD DCE
ADC BAD ABD ADE EDC,∠ADE=∠B,
BAD CDE
△ABD∽△DCE
AD
(2)点 D在 BC边上运动的过程中, 的值不变化,理由如下,
DF
如图,过点A作 AM BC
在Rt ABM 中, AB 10,BM 1 BC 8
2
∠ADE=∠B,
cos BM 4 ADE cos B
AB 5
AF⊥AD
在Rt ADF中
cos ADF AD 4
DF 5
(3)①当 AB AD时,如图,
此时C,D,E重合,
则 AD AC 10
AD 4
由(2)可知
DF 5
EF DF AD 5 25 4 10 则 4 2
5
②当DA DB时,如图,
则 DAB B, ADC 2 B
ADF B
∴ EDC B
DE//AB
CDE∽ CBA
CD DE
CB BA
即DE
AB CD 10 CD 5
CD
CB 16 8
又 ABD∽ DCE
DE DC
AD AB
DE AD DC AD CD即
AB 10
5CD AD CD
8 10
解得 AD
25
4
DE 5 (BC BD) 5 (BC AD) 5 16 25 5 39 195 8 8 8 4 8 4 32
AD 4
DF 5
DF 5 25 125
4 4 16
EF DF DE 125 195 55
16 32 32
③当 BA BD 10,如图,作 AM BC 于M
则 AM 6,MD BD BM 10 8 2 ,CD BC BD BC AB 16 10 6
AD AM 2 MD2 22 62 2 10
AD 4
DF 5
DF AD 4 2 10
5 5
10
4 2
5
又 ABD∽ DCE
DE DC
AD AB
DE AD DC 2 10 6 6则 10
AB 10 5
EF 5 DF DE 10 6 10 13 10
2 5 10
25 55 13
综上所述, EF 的长为 或 或 10
2 32 10
25 55 13
故答案为: 或 或 10
2 32 10
九年级数学
一、选择题(本大题共 10 小题,每小题 4 分,满分 40 分)
1.已知关于 x 的方程 x2 3x a 0有一个根为-2,则 a 的值为( )
A.5 B.2 C.-2 D.-5
k
2.已知反比例函数 y 的图象经过点 (3,2),小良说了四句话,其中正确的是( )
x
A.当 x 0时, y 0 B.函数的图象只在第一象限
C. y随 x的增大而增大 D.点 ( 3,2)不在此函数的图象上
3.如图,在 ABC中,DE∥AC,BD=6cm,DA=3cm,BE=4cm,则 EC的长为( )
A.1cm B.2cm C.3cm D.4cm
4.如图,有一块边长为 6cm的正三角形纸板,在它的三个角处分别截去一个彼此全等的筝形,再沿图中的
虚线折起,做成一个无盖的直三棱柱纸盒,则该纸盒侧面积的最大值是( )
2 3 3 2 9 3 2 27A. 3 cm B. cm C. cm D. 32 cm
2
2 2
5.如图,矩形 ABCD中,AB=3,BC=5,点 P是 BC边上的一个动点(点 P不与点 B,C重合),现将△PCD
沿直线 PD折叠,使点 C落下点 C1处;作∠BPC1的平分线交 AB于点 E.设 BP=x,BE=y,那么 y关于 x
的函数图象大致应为( )
A. B. C. D.
6.如图,已知顶点为(﹣3,﹣6)的抛物线 y=ax2+bx+c经过点(﹣1,﹣4),则下列结论中正确的是( )
A.b2﹣4ac<0
B.ax2+bx+c≥﹣6
C.若点(﹣2,m),(﹣4,n)在抛物线上,则 m>n
D.关于 x的一元二次方程 ax2+bx+c=﹣4的两根为﹣6和﹣1
7.如图,在矩形 ABCD中对角线 AC与 BD相交于点 O,AE⊥BD,垂足为点 E,AE=8,AC=20,则 OE的
长为( )
A.4 3 B.4 C.6 D.8
k
8.如图,曲线 AB是顶点为 B与 y轴交于点A的抛物线 y x2 4x 2的部分,曲线 BC是双曲线 y 的
x
一部分,由点C开始不断重复“ A B C”的过程,形成一组波浪线,点 P 2024,m 与点Q 2032,n 均在该
波浪线上,过点 P、Q分别作 x轴的垂线,垂是为M ,N ,连 PQ,则四边形 PMNQ的面积为( )
A.72 B.36 C.16 D.9
9.如图,已知△ABC和△EDC是以点 C为位似中心的位似图形,且△ABC和△EDC的位似比为 1:2,
△EDC的周长为 8,则△ABC的周长是( )
A.2 B.4 C.8 D.16
10.如图,已知二次函数 y ax2 bx c a 0 的图象与 x轴交于点 A(-1,0),与 y轴的交点在B(0,-2)
和(0,-1)之间(不包括这两点),对称轴为直线 x 1,下列结论不正确的是( )
A.9a 3b c 0 B.4b 3c 0 C. 4ac b2
1 5
4a D. a
3 6
二、填空题(本大题共 4 小题,每小题 5 分,满分 20 分)
1
11.如图, ABC是等边三角形,点 D为 BC边上一点, BD DC 2,以点 D为顶点作正方形 DEFG,
2
且DE BC,连接 AE,AG.若将正方形 DEFG绕点 D旋转一周,当 AE取最小值时,AG的长为________.
12.如图,直线 y x b
k
与 y轴交于点 A,与双曲线 y 在第一象限交于 B,C两点,且 AB AC 4,则
x
k ________.
13.如图,在△ABC中,AD⊥BC,垂足为 D,AD=5,BC=10,四边形 EFGH和四边形 HGNM均为正方
形,且点 E、F、G、N、M都在△ABC的边上,那么△AEM与四边形 BCME的面积比为_______.
14.如图,小明家附近有一观光塔 CD,他发现当光线角度变化时,观光塔的影子在地面上的长度也发生变
化.经测量发现,当小明站在点 A处时,塔顶 D的仰角为 37°,他往前再走 5米到达点 B(点 A,B,C在
3
同一直线上),塔顶 D的仰角为 53°,则观光塔 CD的高度约为 _____(. 精确到 0.1米,参考数值:tan37°≈ ,
4
4
tan53°≈ )
3
三、(本大题共 2 小题,每小题 8 分,满分 16 分)
15.已知抛物线 y=x2+bx+c的图象经过 A(-1,12),B(0,5).
(1)求抛物线解析式;
(2)试判断该二次函数的图象是否经过点(2,3).
16.如图,在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为 1个单位长度的正方形).
(1)将△ABC绕着点 A顺时针旋转 90°,画出旋转后得到的△AB1C1,并直接写出点 B1、C1的坐标.
(2)求线段 AB所扫过的图形的面积.
四、(本大题共 2 小题,每小题 6 分,满分 12 分)
17.某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销 x件.已知产销两种产品的有关信息
如表:
其中 a为常数,且 5≤a≤7.
(1)若产销甲、乙两种产品的年利润分别为 y1万元、 y2万元,直.接.写出 y1、 y2与 x的函数关系式;(注:
年利润=总售价﹣总成本﹣每年其他费用)
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
18.已知二次函数 y=x2﹣4x+3.
(1)用配方法求出顶点坐标;
(2)求该二次函数与坐标轴的交点坐标;
(3)在所给坐标系中画出该二次函数的大致图象,并写出当 y<0时,x的取值范围.
五、(本大题共 1 小题,满分 12 分)
19.通过计算几何图形的面积可以解释代数恒等式的正确性,同样利用几何图形的面积也可以解释不等式
的正确性,请解答下列问题:
(1)根据图①,写出一个代数恒等式,得
(2)两个边长为 a、 b、 c的直角三角形和一个两条直角边均为 c的直角三角形拼成图②,请根据图②中图
形面积的关系写出一个代数恒等式,并写出推导过程;
(3)已知 a、 b、c、a'、b'、 c'均为正数,且满足 a a ' b b ' c c ' m,请画出一个图形,然后利用
该图形面积关系说明 ab ' a 'c bc ' m 2
六、(本大题共 1 小题,满分 14 分)
20.如图,已知抛物线 y ax2 bx 3经过点 A 1,0 和点 B 3,0 ,点 C为抛物线与 y轴的交点.
1 求抛物线的解析式;
2 若点 E为直线 BC上方抛物线上的一点,请求出 BCE面积的最大值.
3 在 2 条件下,是否存在这样的点D 0,m ,使得 BDE为等腰三角形?如果有,请直接写出点 D的坐标;
如果没有,请说明理由.
七、(本大题共 1 小题,满分 8 分)
21.如图,在 ABC中,点D, E,F分别在 AB, BC, AC 边上,DE / /AC,EF / /AB.
(1)求证: BDE∽△EFC.
AF 1
(2)设 ,
FC 2
①若 BC 12,求线段 BE的长;
②若△EFC的面积是 20,求 ABC的面积.
八、(本大题共 1 小题,满分 12 分)
m
22.如图,在平面直角坐标系中,一次函数 y1=kx+b(k≠0)的图象与反比例函数 y2= (m≠0)的图象x
相交于第一、三象限内的 A(3,5),B(a,﹣3)两点,与 x轴交于点 C.
(1)求该反比例函数和一次函数的解析式;
(2)在 y轴上找一点 P使 PB﹣PC最大,求 PB﹣PC的最大值及点 P的坐标;
m
(3)直接写出不等式 kx+b> 的解集.
x
八、(本大题共 1 小题,满分 16 分)
23.如图,在△ABC中,AB=AC=10,BC=16,点 D为 BC边上的动点(点 D不与点 B、C重合). 以点 D
为顶点作∠ADE=∠B,射线 DE交 AC边于点 E,过点 A作 AF⊥AD交射线 DE于点 F,连接 CF.
(1)求证:△ABD∽△DCE;
AD
(2)探索:点 D在 BC边上运动的过程中, 的值是否发生变化?若变化,请说明理由;若不变化,请
DF
求出其值;
(3)当△ABD为等腰三角形时,线段 EF的长为__________.
参考答案
1.B
【解析】根据题意,将 x=-2代入方程 x2+3x+a=0,得:4-6+a=0,
解得:a=2,故选:B.
2.D
k
解:∵反比例函数 y 的图象经过点(3,2),
x
∴k=2×3=6,
y 6∴ ,
x
∴图象在一、三象限,在每个象限 y随 x的增大而减小,故 A,B,C错误,
∴点 ( 3,2)不在此函数的图象上,选项 D正确;
故选:D.
3.B
解:∵DE∥AC,
∴BD:DA=BE:EC,即 6:3=4:EC,
解得:EC=2(cm).故选:B.
4.C
试题解析:∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC.
∵筝形 ADOK≌筝形 BEPF≌筝形 AGQH,
∴AD=BE=BF=CG=CH=AK.
∵折叠后是一个三棱柱,
∴DO=PE=PF=QG=QH=OK,四边形 ODEP、四边形 PFGQ、四边形 QHKO都为矩形.
∴∠ADO=∠AKO=90°.
连结 AO,
在 Rt△AOD和 Rt△AOK中,
AO AO
{
OD OK,
∴Rt△AOD≌Rt△AOK(HL).
∴∠OAD=∠OAK=30°.
设 OD=x,则 AO=2x,由勾股定理就可以求出 AD= 3 x,
∴DE=6-2 3 x,
∴纸盒侧面积=3x(6-2 3 x)=-6 3 x2+18x,
=-6 3 3 9 3(x- )2+ ,
2 2
∴当 x= 3 9 3时,纸盒侧面积最大为 .
2 2
故选 C.
考点:1.二次函数的应用;2.展开图折叠成几何体;3.等边三角形的性质.
5.C
【详解】由翻折的性质得,∠CPD=∠C′PD,
∵PE平分∠BPC1,
∴∠BPE=∠C′PE,
∴∠BPE+∠CPD=90°,
∵∠C=90°,
∴∠CPD+∠PDC=90°,
∴∠BPE=∠PDC,
又∵∠B=∠C=90°,
∴△PCD∽△EBP,
BE PB
∴ ,
PC CD
y x
即 ,
5 x 3
1 1 5 25
∴y= x(5﹣x)=﹣ (x﹣ )2+ ,
3 3 2 12
∴函数图象为 C选项图象.
故选 C.
6.B
【详解】A、图象与 x轴有两个交点,方程 ax2+bx+c=0有两个不相等的实数根,b2﹣4ac>0,
所以 b2>4ac,故 A选项不符合题意;
B、抛物线的开口向上,函数有最小值,因为抛物线的最小值为﹣6,所以 ax2+bx+c≥﹣6,
故 B选项符合题意;
C、抛物线的对称轴为直线 x=﹣3,因为﹣4离对称轴的距离等于﹣2离对称轴的距离,所以
m=n,故 C选项不符合题意;
D、根据抛物线的对称性可知,(﹣1,﹣4)关于对称轴的对称点为(﹣5,﹣4),所以关于
x的一元二次方程 ax2+bx+c=﹣4的两根为﹣5和﹣1,故 D选项不符合题意.
故选 B.
7.C
解:∵四边形 ABCD是矩形,
1
∴AO=CO AC=10,
2
∴OE AO2 AE2 100 64 6.
故选:C.
8.B
【详解】
如图,过点 B作 x轴的垂线交于M ,取 DE的中点Q ,过点Q 作 x轴的垂线交于 N ,
y x2 4x 2 (x 2)2 6,
B(2,6),
把 B(2, 6)
k
代入 y 中得: k 12,
x
12反比例函数解析式为 y ,
x
由图可知,每经过 6为一次循环,
2024 6 337 2, 2032 6 338 4,
点 P离 x轴的距离与点 B离 x轴的距离相同,点 Q离 x轴距离与点Q 离 x轴距离相同,
12
令 x 4代入 y 中得: y 3,
x
Q N 3, BM 6,M N 2032 2024 8,
S 1PMNQ S BM N Q (6 3) 8 36四边形 四边形 .2
故选:B.
9.B
【详解】∵△ABC和△EDC的位似比为 1:2,
∴△ABC和△EDC的相似比为 1:2,
又∵△EDC的周长为 8,
C△ABC C △ABC 1∴ C ,△EDC 8 2
∴△ABC的周长为 4.故选 B.
10.D
【详解】∵ A(-1,0),对称轴为 x 1
∴二次函数与 x 轴的另一个交点为 3,0
将 3,0 2代入 y ax bx c a 0 中
0 9a 3b c,故 A正确
2
将 1,0 , 3,0 代入 y ax bx c a 0 中
0 a b c①
0 9a 3b c②
② 9 ①
0 12b 8c
2c 3b
4b 8 1∴ 3c c 3c c
3 3
∵二次函数与 y轴的交点在B(0,-2)和(0,-1)之间(不包括这两点)
∴ 2 c 1
∴4b 3c
1
c 0
3
∴4b 3c 0,故 B正确;
∵二次函数与 y轴的交点在B(0,-2)和(0,-1)之间(不包括这两点)
4ac b2
∴抛物线顶点纵坐标 1
4a
∵抛物线开口向上
∴ a 0
∴ 4ac b2 4a,故 C正确
∵二次函数与 y轴的交点在B(0,-2)和(0,-1)之间(不包括这两点)
∴ 2 c 1
将 1,0 , 3,0 代入 y ax2 bx c a 0 中
0 a b c①
0 9a 3b c②
① 3 ②
0 12a 4c
c 3a
∴ 2 3a 1
1 a 2∴ ,故 D错误,符合题意
3 3
故答案为:D.
11.8
【详解】过点 A作 AM BC 于 M,
BD 1∵ DC 2,
2
∴DC 4,
∴ BC BD DC 2 4 6,
∵ ABC是等边三角形,
∴ AB AC BC 6,
∵ AM BC ,
BM 1 BC 1∴ 6 3,
2 2
∴DM BM BD 3 2 1,
在RtVABM 中, AM AB2 BM 2 62 32 3 3,
当正方形 DEFG绕点 D旋转到点 E、A、D在同一条直线上时, AD AE DE,
即此时 AE取最小值,
在RtVADM 中, AD DM 2 AM 2 12 (3 3)2 2 7,
∴在RtVADG中, AG AD2 DG2 (2 7)2 62 8;
故答案为 8.
12.2
解:如图所示,过点 B作 BE⊥AO于 E,过点 C作 CF⊥AO于 F,设直线 y x b与 x轴
的交点为 G,
∵A、G分别是直线 y x b与 y轴,x轴的交点,
∴A点坐标为(0,b),G点坐标为(b,0),
∴OA=OG,
∴∠OAG=∠OGA=45°,
∴∠ABE=45°,
∴AE=BE,
∴ AB 2BE,
同理可得 AC 2CF,
设 B点坐标为(m,-m+b),C点坐标为(n,-n+b),
y x b
联立 k 得 x2y bx k 0
,
x
∴mn k,
∵ AB AC 4,
∴ 2m 2n 4,即 2k 4,
∴ k 2.
13.1:3
【详解】
∵四边形 EFGH和四边形 HGNM均为正方形,AD⊥BC,
∴四边形 EFDP是矩形, AP EM ,
∴PD EF EH HM ,
∴设 PD EF EH HM x,
∴ EM 2x, AP 5 x,
∵ EM∥BC,
∴ AEM B, AME C,
∴ AEM∽ ABC,
∵AP和 AD分别是 AEM 和 ABC的高,
AP EM 5 x 2x
∴ ,代入得: ,
AD BC 5 10
x 5 5解得: ,即 PD ,
2 2
∴ AP 5
5 5
,
2 2
5
∴ AP 2 1 ,
AD 5 2
S AEM AP 2 1 2 1
∴ ( ) ( ) S , ABC AD 2 4
∵ S ABC S AEM S四边形BCME,
∴ S AEM : S BCME 1:3四边形 .
故答案为:1:3.
14.8.6米
解:由题意知,∠A=37°,∠DBC=53°,∠D=90°,AB=5,
CD
在 Rt△CBD中,tan∠DBC= ,
BC
CD 3
∴BC= ≈ CD,
tan 53 4
CD CD 3
在 Rt△CAD中,tan∠A= ,即 3
AC 5 CD
=tan37°≈
4 4
60
∴解得:CD= ≈8.6,
7
答:观光塔 CD的高度约为 8.6米.
15.(1) y x2 6x 5;(2)该二次函数的图像不经过点(2,3)
解:(1)抛物线 y x2 bx c的图像经过 A(-1,12),B(0,5).
1 b c 12 b 6
∴ c 5 ,解得: , c 5
二次函数解析式为: y x2 6x 5;
(2)当 x=2时,y=x2-6x+5=4-12+5=-3,
∴该二次函数的图象不经过点(2,3).
16.
【详解】(1)如图所示,△AB1C1即为所求;
由图可知点 B1的坐标为(4,﹣2)、C1的坐标为(1,﹣3);
(2)∵AB= 32 32 =3 2,且∠BAB1=90°,
2
AB 90 3 2
9
∴线段 所扫过的图形的面积为 = π.
360 2
17.【解析】
(1) 解:(1)y1=(8-a)x-20,(0<x≤200)
y 10x 30 0.05x22 = 0.05x2 10x 30.(0<x≤90).
(2)对于 y1=(8-a)x-20.
∵8-a>0,∴x=200时,y1的值最大=(1580-200a)万元.
对于 y2 0.05 x 100
2 470.
∵0<x≤90,∴x=90时, y2最大值=465万元.
(3)①(1580-200a)=465,解得 a=5.575,②(1580-200a)>465,解得 a<5.575,③(1580-200a)
<465,解得 a>5.575.
∵5≤a≤7,∴当 a=5.575时,生产甲乙两种产品的利润相同.
当 5≤a<5.575时,生产甲产品利润比较高.
当 5.575<a≤7时,生产乙产品利润比较高.
18.(1)顶点坐标为(2,-1);(2)该二次函数与 x轴的交点坐标为(1,0)(3,0);(3)
当 y<0时,1<x<3.
解:(1)因为 y=x2-4x+3=x2-4x+4-1=(x-2)2-1,
所以抛物线的顶点坐标为(2,-1);
(2)当 y=0时,x2-4x+3=0,解得 x1=1,x2=3,
所以该二次函数与 x轴的交点坐标为(1,0)(3,0);
(2)当 x=0时,y=3,当 x=4时,y= 42-4 4+3=3,
描点,连线,函数图象如图:
由图象可知,当 y<0时,1<x<3.
19.(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;(2)过程见详解;(3)过程见详解
解:(1)由图①可得:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)a2+b2=c2,证明如下:
1
梯形的面积为: 2 (a+b)(a+b
1 1
)= 2 ab×2+
2
2 c ,
化简即可得:a2+b2=c2;
(3)构造一个边长为 m的正方形,如图所示:
显然 a a ' b b ' c c ' m,
根据图形可知,正方形内部 3个矩形的面积和小于正方形的面积,
ab ' a 'c bc ' m2.
20.(1) y x2 2x 3.(2)当 n
3
时, BCE 27面积取最大值,最大值为 .(3)点 D
2 8
的坐标为 0,0 、 0,
15
、 0,
39
、 0,
3 13 3 13
或 0,
2 40 4 4
详解: 1 将 A 1,0 、B 3,0 代入 y ax2 bx 3,
a b 3 0 a 1得: 9a 3b 3 0,解得: b 2,
抛物线的解析式为 y x2 2x 3.
2 过点 E作 EF / / y轴,交 BC于点 F,如图 1所示.
当 x 0时, y x2 2x 3 3,
点 C的坐标为 0,3 .
设直线 BC的解析式为 y kx c,
将B 3,0 、C 0,3 代入 y kx c,得:
3k b 0 k 1b 3,解得: b 3,
直线 BC的解析式为 y x 3.
2
设点 E的坐标为 n, n 2n 3 ,则点 F的坐标为 n, n 3 ,
EF n2 2n 3 n 3 n2 3n,
S 1 3 2 9 3 3 2 27 BCE EF OB n n (n ) ,2 2 2 2 2 8
n 3 BCE 27当 时, 面积取最大值,最大值为 .
2 8
3 2 3由 可知点 E的坐标为 ,
15
2 4
.
BDE为等腰三角形分三种情况 (如图 2):
3
①当 ED EB时,有 ( )2 (
15
m)2 (3 3)2 (15)2 ,
2 4 2 4
解得:m 0 m
15
1 , 2 ,2
15
点 D的坐标为 0,0 或 0, 2 ;
② DE DB (3 0)2 2
3 15
当 时,有 (0 m) ( 0)2 ( m)2,
2 4
39
解得:m3 ,40
39 点 D的坐标为 0, ;
40
2 2 3 15③当 BD BE时,有 (3 0) (0 m) ( 3)2 ( )2,
2 4
m 3 13 m 3 13解得: 4 , 5 ,4 4
点 D的坐标为 0,
3 13 0, 3 13
4
或 4
.
0,0 0,15 0, 39
0, 3 13
3 13
综上所述:当点 D的坐标为 、 2 、 、 或
0, 时,
40 4
BDE
4
为等腰三角形.
21.
( 1)证明:∵DE∥AC,
∴∠BED=∠C,
又∵EF∥AB,
∴∠B=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
BE AF 1
∴ ,
EC FC 2
∵BC=12,
BE 1
∴ ,
12 BE 2
∴BE=4;
AF 1
②∵ ,
FC 2
CF 2
∴ ,
AC 3
∵EF∥AB,
∴∠CEF=∠B,
∵∠C=∠C.
∴△EFC∽△BAC,
S EFC CF 2 4
∴ ( ) S , ABC AC 9
∵S△EFC=20,
4
∴S△ABC=20÷ =45.9
15
22.(1)y1=x+2,y2= ;(2)最大值3 2,P(0,2);(3)﹣5<x<0或 x>3x
m
解:(1)把 A(3,5)代入 y2= (m≠0),可得 m=3×5=15,x
15
∴反比例函数的解析式为 y2= ,x
把点 B(a,﹣3)代入,可得 a=﹣5,
∴B(﹣5,﹣3).
把 A(3,5),B(﹣5,﹣3)代入 y1=kx+b,
3k+b=5
可得 ,
5k+b=3
k=1
解得 ,
b=2
∴一次函数的解析式为 y1=x+2;
(2)一次函数的解析式为 y1=x+2,令 x=0,则 y=2,
∴一次函数与 y轴的交点为 P(0,2),
此时,PB﹣PC=BC最大,P即为所求,
令 y=0,则 x=﹣2,
∴C(﹣2,0),
过 B点向 x轴作垂线,由勾股定理可得:
BC 5 2 2 32 3 2;
(3)∵A(3,5),B(﹣5,﹣3)
∴根据函数图象可知,当 y1>y2时,﹣5<x<0或 x>3.
m
即 kx+b> 的解集为:﹣5<x<0或 x>3.
x
AD AD 4 25 55 13
23.(1)见解析;(2) 的值不发生变化, 的值为 ;(3) 或 或 10
DF DF 5 2 32 10
(1)证明: AB AC
ABD DCE
ADC BAD ABD ADE EDC,∠ADE=∠B,
BAD CDE
△ABD∽△DCE
AD
(2)点 D在 BC边上运动的过程中, 的值不变化,理由如下,
DF
如图,过点A作 AM BC
在Rt ABM 中, AB 10,BM 1 BC 8
2
∠ADE=∠B,
cos BM 4 ADE cos B
AB 5
AF⊥AD
在Rt ADF中
cos ADF AD 4
DF 5
(3)①当 AB AD时,如图,
此时C,D,E重合,
则 AD AC 10
AD 4
由(2)可知
DF 5
EF DF AD 5 25 4 10 则 4 2
5
②当DA DB时,如图,
则 DAB B, ADC 2 B
ADF B
∴ EDC B
DE//AB
CDE∽ CBA
CD DE
CB BA
即DE
AB CD 10 CD 5
CD
CB 16 8
又 ABD∽ DCE
DE DC
AD AB
DE AD DC AD CD即
AB 10
5CD AD CD
8 10
解得 AD
25
4
DE 5 (BC BD) 5 (BC AD) 5 16 25 5 39 195 8 8 8 4 8 4 32
AD 4
DF 5
DF 5 25 125
4 4 16
EF DF DE 125 195 55
16 32 32
③当 BA BD 10,如图,作 AM BC 于M
则 AM 6,MD BD BM 10 8 2 ,CD BC BD BC AB 16 10 6
AD AM 2 MD2 22 62 2 10
AD 4
DF 5
DF AD 4 2 10
5 5
10
4 2
5
又 ABD∽ DCE
DE DC
AD AB
DE AD DC 2 10 6 6则 10
AB 10 5
EF 5 DF DE 10 6 10 13 10
2 5 10
25 55 13
综上所述, EF 的长为 或 或 10
2 32 10
25 55 13
故答案为: 或 或 10
2 32 10
同课章节目录
