4.4比的应用(课件)- 数学六年级上册(共20张PPT)人教版
文档属性
| 名称 | 4.4比的应用(课件)- 数学六年级上册(共20张PPT)人教版 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 16:16:35 | ||
图片预览








文档简介
(共20张PPT)
4.3 比的应用
驻马店市第十八中学 六(1)班 张铭哲
四大发明——火药
火药的发现,是一个美丽的意外。
相传南北朝著名的炼丹师葛洪,因为又一次炼丹在炼丹炉中无意放入了硫磺、硝石等,造成炼丹炉爆炸。但是,这样的意外并没有促进黑火药的诞生,随着炼丹意外的增加,人们逐渐发现了火药的成分。
到唐朝中期,人们终于摸索出黑火药配方:“一硫二硝三木炭”,即一份硫磺,加两份硝石配合三份木炭。
而黑火药真正用于战场则是在唐朝末期。904年,江南军阀杨行密的军队围攻豫章城,部将郑瑶“以所部发机飞火,烧龙沙门,带领壮士突火先登入城,焦灼被体”,这就是“豫章飞火”的来历,也是世界上最早的火药运用于战争的记载。
温故知新
(1)2020年是新冠疫情肆虐的一年,为了保护师生的身体健康,我校决定对校园进行全面消杀。消杀工作需要“84”消毒液,在使用之前需要把浓缩液加水稀释成稀释液,每10ml浓缩液需要加水1000ml,请回答下列问题:
配制好的消毒液中,浓缩液和水的比是多少?
浓缩液和水的最简整数比是多少?它的比值是多少?
(2)六(1)班64名同学参加大扫除,其中的同学打扫教室,的同学打扫操场。
(1)打扫教室、操场的同学各有多少人?
打扫教室 打扫操场
(2)写出打扫教室、操场的人数比。
问题提出
(1)在上面的题目中,有的同学去打扫教室, 有的同学去打扫操场。
(2)打扫教室和打扫操场的同学的人数之比为 ( ): ( )
(3)在分配打扫教室和打扫操场的同学时,我们把全班同学分成了( )组,其中( )组去打扫教室,( )组去打扫操场。
3 5
8 3 5
问题提出
在完成分配工作时,我们怎么样才能做到按比例分配?
典例探究
这是某种清洁剂浓缩
液的稀释瓶,瓶子上
标明的比表示浓缩液
和水的体积之比。按
照这些比,可以配制
出不同浓度的稀释液。
阅读理解
配置好的稀释液有多少mL?
500ml
“1:4”的前项和后项分别代表的是谁的体积?为了做到1:4的分配,应该把总体积分为几份?
前项是浓缩液的体积,后项是水的体积
1:4指的是1份浓缩液需要搭配4份水
总体积被分为5份
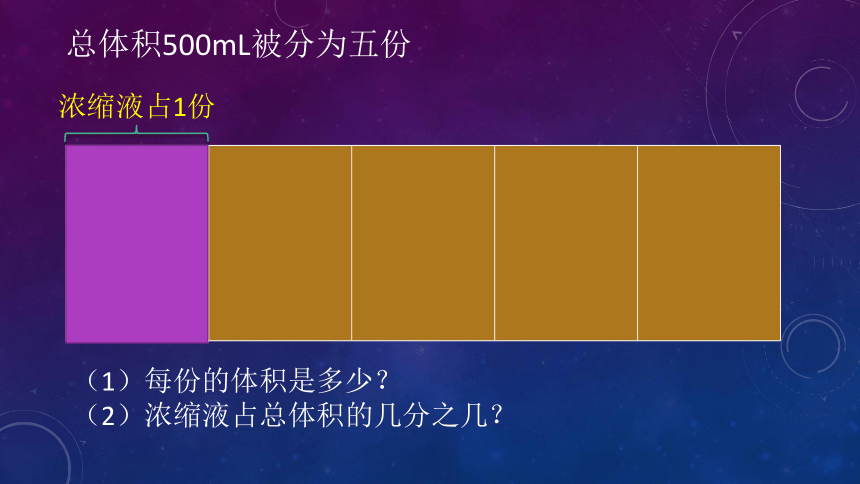
总体积500mL被分为五份
浓缩液占1份
(1)每份的体积是多少?
(2)浓缩液占总体积的几分之几?
先算每份代表的体积?(浓缩液有几份?水有几份?)
先算两个分量占整体的几分之几?(浓缩液的体积占了总体积的几分之几?水的体积又占了总体积的几分之几?)
先算每份的体积
每份是:
浓缩液有:
水有:
答:浓缩液有,水有
利用浓缩液占总体积的几分之几计算
浓缩液有:
水有:
答:浓缩液有,水有
归纳总结
在解决按比例分配问题时:
①阅读条件,弄清楚题目中的比例是哪两个或者哪几个量之比。
②把比例式转换成每个量所占的份数
例如:桃树和李树的比例是2:3,那么:
桃树占2份,李树占3份,一共有5份
③确定每一份是多少,或者是每个部分的量各占整体的几分之几,根据条件列出算式求解。
初试身手(试着先算算每份有多少人?)
某妇产医院上月新生婴儿303名,男女婴儿人数之比是51︰50。上月新生男、女婴儿各有多少人?
所有的婴儿
每份
女婴
男婴
答:上月新生男婴153人,女婴150人。
初试身手(试着写出蜂蜜和水分别占一杯的几分之几?)
蜂蜜有:
水有:
答:需要蜂蜜,需要水。
可以用1份蜂蜜和9份水来冲兑蜂蜜水。
这个杯子的容积正好是200mL,要冲兑一满杯这样的蜂蜜水,需要蜂蜜和水各多少毫升?
我发现了
整体的份数,就相当于所有分量的份数之和。所以,要每个分量占整体的几分之几,只需要求:
分量的份数除以总份数。
即:
分量占整体的几分之几=
挑战自我
学校买回120本新图书,按3:4:5分给三、四、五年级,三、四、五年级各分得多少本?
提示:三、四、五年级各占了几份?那么,一共有多少份?
三年级分得:
四年级分得:
五年级分得:
答:三年级份30本,四年级份40本,五年级分50本。
挑战自我
2、幼儿园午饭分包子,按3:4:5的比分配给小班、中班、大班,中班分了60个,一共有多少个包子?
提示:中班分得了几份?每份有多少个?
每份有:
一共有包子:
答:一共有180个包子。
挑战自我——也可以这么做……
求解“一共有多少个包子”,就是求解单位“1”是多少,所以我可以列方程求解这个问题。
2、幼儿园午饭分包子,按3:4:5的比分配给小班、中班、大班,中班分了60个,一共有多少个包子?
解: 设一共有个包子。
答:一共有个包子。
fin
Thanks for listening!
学习数学和学习一切科学一样,是没有什么捷径可走的。学习数学,人人都得独立思考,就像种庄稼一样,不耕耘是不会有收获的。
——第一位系统阐述“黄金分割比”的数学家,欧几里得。
4.3 比的应用
驻马店市第十八中学 六(1)班 张铭哲
四大发明——火药
火药的发现,是一个美丽的意外。
相传南北朝著名的炼丹师葛洪,因为又一次炼丹在炼丹炉中无意放入了硫磺、硝石等,造成炼丹炉爆炸。但是,这样的意外并没有促进黑火药的诞生,随着炼丹意外的增加,人们逐渐发现了火药的成分。
到唐朝中期,人们终于摸索出黑火药配方:“一硫二硝三木炭”,即一份硫磺,加两份硝石配合三份木炭。
而黑火药真正用于战场则是在唐朝末期。904年,江南军阀杨行密的军队围攻豫章城,部将郑瑶“以所部发机飞火,烧龙沙门,带领壮士突火先登入城,焦灼被体”,这就是“豫章飞火”的来历,也是世界上最早的火药运用于战争的记载。
温故知新
(1)2020年是新冠疫情肆虐的一年,为了保护师生的身体健康,我校决定对校园进行全面消杀。消杀工作需要“84”消毒液,在使用之前需要把浓缩液加水稀释成稀释液,每10ml浓缩液需要加水1000ml,请回答下列问题:
配制好的消毒液中,浓缩液和水的比是多少?
浓缩液和水的最简整数比是多少?它的比值是多少?
(2)六(1)班64名同学参加大扫除,其中的同学打扫教室,的同学打扫操场。
(1)打扫教室、操场的同学各有多少人?
打扫教室 打扫操场
(2)写出打扫教室、操场的人数比。
问题提出
(1)在上面的题目中,有的同学去打扫教室, 有的同学去打扫操场。
(2)打扫教室和打扫操场的同学的人数之比为 ( ): ( )
(3)在分配打扫教室和打扫操场的同学时,我们把全班同学分成了( )组,其中( )组去打扫教室,( )组去打扫操场。
3 5
8 3 5
问题提出
在完成分配工作时,我们怎么样才能做到按比例分配?
典例探究
这是某种清洁剂浓缩
液的稀释瓶,瓶子上
标明的比表示浓缩液
和水的体积之比。按
照这些比,可以配制
出不同浓度的稀释液。
阅读理解
配置好的稀释液有多少mL?
500ml
“1:4”的前项和后项分别代表的是谁的体积?为了做到1:4的分配,应该把总体积分为几份?
前项是浓缩液的体积,后项是水的体积
1:4指的是1份浓缩液需要搭配4份水
总体积被分为5份
总体积500mL被分为五份
浓缩液占1份
(1)每份的体积是多少?
(2)浓缩液占总体积的几分之几?
先算每份代表的体积?(浓缩液有几份?水有几份?)
先算两个分量占整体的几分之几?(浓缩液的体积占了总体积的几分之几?水的体积又占了总体积的几分之几?)
先算每份的体积
每份是:
浓缩液有:
水有:
答:浓缩液有,水有
利用浓缩液占总体积的几分之几计算
浓缩液有:
水有:
答:浓缩液有,水有
归纳总结
在解决按比例分配问题时:
①阅读条件,弄清楚题目中的比例是哪两个或者哪几个量之比。
②把比例式转换成每个量所占的份数
例如:桃树和李树的比例是2:3,那么:
桃树占2份,李树占3份,一共有5份
③确定每一份是多少,或者是每个部分的量各占整体的几分之几,根据条件列出算式求解。
初试身手(试着先算算每份有多少人?)
某妇产医院上月新生婴儿303名,男女婴儿人数之比是51︰50。上月新生男、女婴儿各有多少人?
所有的婴儿
每份
女婴
男婴
答:上月新生男婴153人,女婴150人。
初试身手(试着写出蜂蜜和水分别占一杯的几分之几?)
蜂蜜有:
水有:
答:需要蜂蜜,需要水。
可以用1份蜂蜜和9份水来冲兑蜂蜜水。
这个杯子的容积正好是200mL,要冲兑一满杯这样的蜂蜜水,需要蜂蜜和水各多少毫升?
我发现了
整体的份数,就相当于所有分量的份数之和。所以,要每个分量占整体的几分之几,只需要求:
分量的份数除以总份数。
即:
分量占整体的几分之几=
挑战自我
学校买回120本新图书,按3:4:5分给三、四、五年级,三、四、五年级各分得多少本?
提示:三、四、五年级各占了几份?那么,一共有多少份?
三年级分得:
四年级分得:
五年级分得:
答:三年级份30本,四年级份40本,五年级分50本。
挑战自我
2、幼儿园午饭分包子,按3:4:5的比分配给小班、中班、大班,中班分了60个,一共有多少个包子?
提示:中班分得了几份?每份有多少个?
每份有:
一共有包子:
答:一共有180个包子。
挑战自我——也可以这么做……
求解“一共有多少个包子”,就是求解单位“1”是多少,所以我可以列方程求解这个问题。
2、幼儿园午饭分包子,按3:4:5的比分配给小班、中班、大班,中班分了60个,一共有多少个包子?
解: 设一共有个包子。
答:一共有个包子。
fin
Thanks for listening!
学习数学和学习一切科学一样,是没有什么捷径可走的。学习数学,人人都得独立思考,就像种庄稼一样,不耕耘是不会有收获的。
——第一位系统阐述“黄金分割比”的数学家,欧几里得。
