2021-2022学年人教版八年级数学下册16.3二次根式的加减 知识点分类训练(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册16.3二次根式的加减 知识点分类训练(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学下册《16-3二次根式的加减》知识点分类训练(附答案)
一.可以合并的二次根式
1.下列二次根式中,与可以合并的是( )
A. B. C. D.
2.若最简二次根式和能合并,则a、b的值分别是( )
A.2和1 B.1和2 C.2和2 D.1和1
3.如果最简二次根式与可以合并,那么3的值为 .
4.最简二次根式和可以合并,则a= ,b= .
5.如果最简二次根式与可以合并,那么a= .
6.已知二次根式﹣.
(1)求使得该二次根式有意义的x的取值范围;
(2)已知﹣为最简二次根式,且与可以合并,求x的值,并求出这两个二次根式的积.
二.二次根式的加减法
7.下列运算正确的是( )
A.+= B.﹣x2y3 2xy2=﹣2x2y6
C.(m﹣n)2=m2﹣n2 D.
8.实数a、b在数轴上的位置如图所示,化简代数式,结果为( )
A.2a B.2b C.﹣2a D.2
9.已知a,b为实数,ab=3,a+b=﹣6.
(1)a2b+ab2= ;
(2)a+b= .
10.已知a+b=﹣5,ab=2,且a≠b,则化简b+a= .
11.已知x=+,y=+,比较x与y的大小.
12.计算:
(1)+;
(2)(+)+( ﹣).
三.二次根式的混合运算
13.下列计算中,正确的是( )
A.
B.
C.
D.
14.已知:,则ab3+a3b的值为 .
15.计算:(﹣)(+)= .
16.计算:
(1)÷+2×﹣(2+)2
(2)(﹣)﹣2﹣(﹣1)2022×﹣+
17.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:.
四.二次根式的化简求值
18.若x﹣y=+1,xy=,则代数式(x﹣1)(y+1)的值等于( )
A.2+2 B.2﹣2 C.2 D.2
19.已知x=+1,y=﹣1,则x2﹣y2的值为 .
20.若a=,b=,则= .(结果用含t的式子表示)
21.已知:a=﹣1,求÷(2﹣)的值.
22.小明在解决问题:已知a=,求2a2﹣8a+1的值,他是这样分析与解的:
∵a===2﹣,
∴a﹣2=﹣,
∴(a﹣2)2=3,a2﹣4a+4=3,
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)化简+++…+;
(2)若a=,求4a2﹣8a+1的值.
五.二次根式的应用
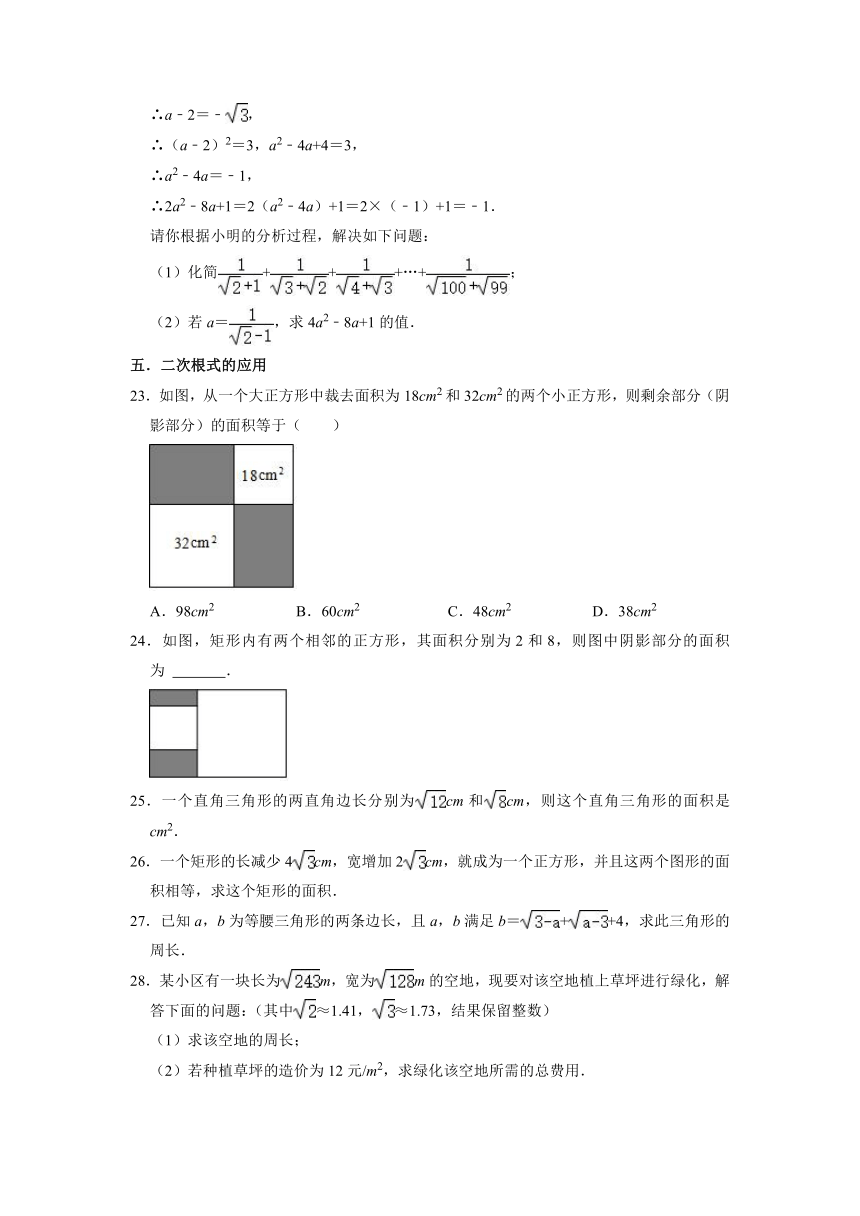
23.如图,从一个大正方形中裁去面积为18cm2和32cm2的两个小正方形,则剩余部分(阴影部分)的面积等于( )
A.98cm2 B.60cm2 C.48cm2 D.38cm2
24.如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为 .
25.一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的面积是 cm2.
26.一个矩形的长减少4cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等,求这个矩形的面积.
27.已知a,b为等腰三角形的两条边长,且a,b满足b=++4,求此三角形的周长.
28.某小区有一块长为m,宽为m的空地,现要对该空地植上草坪进行绿化,解答下面的问题:(其中≈1.41,≈1.73,结果保留整数)
(1)求该空地的周长;
(2)若种植草坪的造价为12元/m2,求绿化该空地所需的总费用.
参考答案
一.可以合并的二次根式
1.解:A、原式=,不符合题意;
B、原式=3,符合题意;
C、原式=,不符合题意;
D、原式=3,不符合题意.
故选:B.
2.解:∵最简二次根式和能合并,
∴,即,
①×2+②得:7a=7,
解得:a=1,
把a=1代入②得:1+2b=3,
解得:b=1.
故选:D.
3.解:由题意得3a+8=12﹣a,
解得a=1,
当a=1时3=3.
故答案为:3.
4.解:由最简二次根式和可以合并,得
,
解得,
故答案为:2,0.
5.解:∵最简二次根式与可以合并,
∴1+a=4a﹣2,
解得a=1.
故答案为1.
6.解:(1)要使﹣有意义,必须x﹣2≥0,
即x≥2,
所以使得该二次根式有意义的x的取值范围是x≥2;
(2)=,
所以x﹣2=10,
解得:x=12,
这两个二次根式的积为﹣×=﹣5.
二.二次根式的加减法
7.解:A选项,与不是同类二次根式,不能合并,故该选项不符合题意;
B选项,原式=﹣2x3y5,故该选项不符合题意;
C选项,原式=m2﹣2mn+n2,故该选项不符合题意;
D选项,原式= =a﹣2,故该选项符合题意;
故选:D.
8.解:∵
=|a﹣b|+|b﹣|﹣a﹣
=b﹣a+﹣b﹣a﹣
=﹣2a;
故选:C.
9.解:(1)原式=ab(a+b)
=3×(﹣6)
=﹣18;
(2)∵ab=3>0,
∴a,b同号,
又∵a+b=﹣6<0,
∴a<0,b<0.
原式=﹣(﹣a)﹣(﹣b)
=﹣﹣
=﹣﹣
=﹣2
=﹣2.
故答案为:(1)﹣18;(2)﹣2.
10.解:∵a+b=﹣5,ab=2,
∴b+a=﹣b ﹣
=﹣
=﹣
=﹣
=﹣.
故答案为:﹣.
11.解:x2=12+2、y2=12+2,
因为大于,
所以 x>y.
12.解:(1)+
=2+5
=7;
(2)(+)+( ﹣)
=4+2+2﹣
=6+.
三.二次根式的混合运算(共5小题)
13.解:A、原式=5﹣2+3=8﹣2,故A不符合题意.
B、原式=×+×=+,故B不符合题意.
C、原式=a﹣+﹣,故C不符合题意.
D、原式=3﹣2=1,故D符合题意.
故选:D.
14.解:∵,
∴a+b=+=,
ab=×==,
则原式=ab(a2+b2)
=ab[(a+b)2﹣2ab]
=×(3﹣2×)
=×
=,
故答案为:.
15.解:原式=5﹣3=2,
故答案为2.
16.解:(1)原式=+2﹣(8+4+3)
=4+2﹣11﹣4
=﹣7﹣2;
(2)原式=4﹣1×1﹣4+5
=4﹣1﹣4+5
=4.
17.解:(1)a+b=(m+n)2,
∵a+b=m2+3n2+2mn,
∴a=m2+3n2,b=2mn,
故答案为:m2+3n2;2mn;
(2)7+4=(2+)2;
(3)∵a是216的立方根,b是16的平方根,
∴a=6,b=±4,
∴===2±.
四.二次根式的化简求值(共5小题)
18.解:当x﹣y=+1,xy=时,
原式=xy+x﹣y﹣1
=++1﹣1
=2,
故选:C.
19.解:∵x=+1,y=﹣1,
∴x+y=+1+﹣1=2,
x﹣y=+1﹣+1=2,
则原式=(x+y)(x﹣y)
=2×2
=4,
故答案为:4.
20.解:∵a=,b=,
∴a+b=+=﹣1,
ab=×
==t,
∴=
=﹣t,
故答案为:﹣t.
21.解:原式=÷(﹣),
=÷,
= ,
=a(a+2),
当a=﹣1时,
原式=(﹣1)(﹣1+2)=(﹣1)(1)=2﹣1=1.
22.解:(1)原式=(﹣1)+(﹣)+(﹣)+…+(﹣)=﹣1=10﹣1=9;
(2)a==+1,
∴a﹣1=,
∴(a﹣1)2=2,a2﹣2a+1=2,
∴a2﹣2a=1,
∴原式=4(a2﹣2a)+1=4×1+1=5.
五.二次根式的应用(共6小题)
23.解:如图.
由题意知:,.
∴BC=(cm),HG=(cm).
∵四边形BCDM是正方形,四边形HMFG是正方形,
∴BC=BM=MD=cm,HM=HG=MF=cm.
∴S阴影部分=S矩形ABMH+S矩形MDEF
=BM HM+MD MF
=
=48(cm2).
故选:C.
24.解:由题意可得,
大正方形的边长为,小正方形的边长为,
∴图中阴影部分的面积为:×(2﹣)=2,
故答案为:2.
25.解:这个直角三角形的面积=cm2,
故答案为:2
26.解:设矩形的长为xcm,宽为ycm,
根据题意,得,
解这个方程组得:,
所以,矩形的面积为8×2=16×3=48cm2.
27.解:
∵b=++4,
∴a﹣3≥0且3﹣a≥0,
∴a=3,
∴b=4,
当a为等腰三角形的腰时,则此三角形周长为3+3+4=10,
当b为等腰三角形的腰时,则此三角形周长为4+4+3=11.
28.解:(1)由题意可得,
该空地的周长是:(+)×2=(9+8)×2≈(9×1.73+8×1.41)×2=53.7≈54(m),
即该空地的周长是54m;
(2)由题意可得,
绿化该空地所需的总费用是:=≈9×1.73×8×1.41×12≈2108(元),
答:绿化该空地所需的总费用是2108元.
一.可以合并的二次根式
1.下列二次根式中,与可以合并的是( )
A. B. C. D.
2.若最简二次根式和能合并,则a、b的值分别是( )
A.2和1 B.1和2 C.2和2 D.1和1
3.如果最简二次根式与可以合并,那么3的值为 .
4.最简二次根式和可以合并,则a= ,b= .
5.如果最简二次根式与可以合并,那么a= .
6.已知二次根式﹣.
(1)求使得该二次根式有意义的x的取值范围;
(2)已知﹣为最简二次根式,且与可以合并,求x的值,并求出这两个二次根式的积.
二.二次根式的加减法
7.下列运算正确的是( )
A.+= B.﹣x2y3 2xy2=﹣2x2y6
C.(m﹣n)2=m2﹣n2 D.
8.实数a、b在数轴上的位置如图所示,化简代数式,结果为( )
A.2a B.2b C.﹣2a D.2
9.已知a,b为实数,ab=3,a+b=﹣6.
(1)a2b+ab2= ;
(2)a+b= .
10.已知a+b=﹣5,ab=2,且a≠b,则化简b+a= .
11.已知x=+,y=+,比较x与y的大小.
12.计算:
(1)+;
(2)(+)+( ﹣).
三.二次根式的混合运算
13.下列计算中,正确的是( )
A.
B.
C.
D.
14.已知:,则ab3+a3b的值为 .
15.计算:(﹣)(+)= .
16.计算:
(1)÷+2×﹣(2+)2
(2)(﹣)﹣2﹣(﹣1)2022×﹣+
17.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为整数),则有a+b=m2+2n2+2mn.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:.
四.二次根式的化简求值
18.若x﹣y=+1,xy=,则代数式(x﹣1)(y+1)的值等于( )
A.2+2 B.2﹣2 C.2 D.2
19.已知x=+1,y=﹣1,则x2﹣y2的值为 .
20.若a=,b=,则= .(结果用含t的式子表示)
21.已知:a=﹣1,求÷(2﹣)的值.
22.小明在解决问题:已知a=,求2a2﹣8a+1的值,他是这样分析与解的:
∵a===2﹣,
∴a﹣2=﹣,
∴(a﹣2)2=3,a2﹣4a+4=3,
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)化简+++…+;
(2)若a=,求4a2﹣8a+1的值.
五.二次根式的应用
23.如图,从一个大正方形中裁去面积为18cm2和32cm2的两个小正方形,则剩余部分(阴影部分)的面积等于( )
A.98cm2 B.60cm2 C.48cm2 D.38cm2
24.如图,矩形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为 .
25.一个直角三角形的两直角边长分别为cm和cm,则这个直角三角形的面积是 cm2.
26.一个矩形的长减少4cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等,求这个矩形的面积.
27.已知a,b为等腰三角形的两条边长,且a,b满足b=++4,求此三角形的周长.
28.某小区有一块长为m,宽为m的空地,现要对该空地植上草坪进行绿化,解答下面的问题:(其中≈1.41,≈1.73,结果保留整数)
(1)求该空地的周长;
(2)若种植草坪的造价为12元/m2,求绿化该空地所需的总费用.
参考答案
一.可以合并的二次根式
1.解:A、原式=,不符合题意;
B、原式=3,符合题意;
C、原式=,不符合题意;
D、原式=3,不符合题意.
故选:B.
2.解:∵最简二次根式和能合并,
∴,即,
①×2+②得:7a=7,
解得:a=1,
把a=1代入②得:1+2b=3,
解得:b=1.
故选:D.
3.解:由题意得3a+8=12﹣a,
解得a=1,
当a=1时3=3.
故答案为:3.
4.解:由最简二次根式和可以合并,得
,
解得,
故答案为:2,0.
5.解:∵最简二次根式与可以合并,
∴1+a=4a﹣2,
解得a=1.
故答案为1.
6.解:(1)要使﹣有意义,必须x﹣2≥0,
即x≥2,
所以使得该二次根式有意义的x的取值范围是x≥2;
(2)=,
所以x﹣2=10,
解得:x=12,
这两个二次根式的积为﹣×=﹣5.
二.二次根式的加减法
7.解:A选项,与不是同类二次根式,不能合并,故该选项不符合题意;
B选项,原式=﹣2x3y5,故该选项不符合题意;
C选项,原式=m2﹣2mn+n2,故该选项不符合题意;
D选项,原式= =a﹣2,故该选项符合题意;
故选:D.
8.解:∵
=|a﹣b|+|b﹣|﹣a﹣
=b﹣a+﹣b﹣a﹣
=﹣2a;
故选:C.
9.解:(1)原式=ab(a+b)
=3×(﹣6)
=﹣18;
(2)∵ab=3>0,
∴a,b同号,
又∵a+b=﹣6<0,
∴a<0,b<0.
原式=﹣(﹣a)﹣(﹣b)
=﹣﹣
=﹣﹣
=﹣2
=﹣2.
故答案为:(1)﹣18;(2)﹣2.
10.解:∵a+b=﹣5,ab=2,
∴b+a=﹣b ﹣
=﹣
=﹣
=﹣
=﹣.
故答案为:﹣.
11.解:x2=12+2、y2=12+2,
因为大于,
所以 x>y.
12.解:(1)+
=2+5
=7;
(2)(+)+( ﹣)
=4+2+2﹣
=6+.
三.二次根式的混合运算(共5小题)
13.解:A、原式=5﹣2+3=8﹣2,故A不符合题意.
B、原式=×+×=+,故B不符合题意.
C、原式=a﹣+﹣,故C不符合题意.
D、原式=3﹣2=1,故D符合题意.
故选:D.
14.解:∵,
∴a+b=+=,
ab=×==,
则原式=ab(a2+b2)
=ab[(a+b)2﹣2ab]
=×(3﹣2×)
=×
=,
故答案为:.
15.解:原式=5﹣3=2,
故答案为2.
16.解:(1)原式=+2﹣(8+4+3)
=4+2﹣11﹣4
=﹣7﹣2;
(2)原式=4﹣1×1﹣4+5
=4﹣1﹣4+5
=4.
17.解:(1)a+b=(m+n)2,
∵a+b=m2+3n2+2mn,
∴a=m2+3n2,b=2mn,
故答案为:m2+3n2;2mn;
(2)7+4=(2+)2;
(3)∵a是216的立方根,b是16的平方根,
∴a=6,b=±4,
∴===2±.
四.二次根式的化简求值(共5小题)
18.解:当x﹣y=+1,xy=时,
原式=xy+x﹣y﹣1
=++1﹣1
=2,
故选:C.
19.解:∵x=+1,y=﹣1,
∴x+y=+1+﹣1=2,
x﹣y=+1﹣+1=2,
则原式=(x+y)(x﹣y)
=2×2
=4,
故答案为:4.
20.解:∵a=,b=,
∴a+b=+=﹣1,
ab=×
==t,
∴=
=﹣t,
故答案为:﹣t.
21.解:原式=÷(﹣),
=÷,
= ,
=a(a+2),
当a=﹣1时,
原式=(﹣1)(﹣1+2)=(﹣1)(1)=2﹣1=1.
22.解:(1)原式=(﹣1)+(﹣)+(﹣)+…+(﹣)=﹣1=10﹣1=9;
(2)a==+1,
∴a﹣1=,
∴(a﹣1)2=2,a2﹣2a+1=2,
∴a2﹣2a=1,
∴原式=4(a2﹣2a)+1=4×1+1=5.
五.二次根式的应用(共6小题)
23.解:如图.
由题意知:,.
∴BC=(cm),HG=(cm).
∵四边形BCDM是正方形,四边形HMFG是正方形,
∴BC=BM=MD=cm,HM=HG=MF=cm.
∴S阴影部分=S矩形ABMH+S矩形MDEF
=BM HM+MD MF
=
=48(cm2).
故选:C.
24.解:由题意可得,
大正方形的边长为,小正方形的边长为,
∴图中阴影部分的面积为:×(2﹣)=2,
故答案为:2.
25.解:这个直角三角形的面积=cm2,
故答案为:2
26.解:设矩形的长为xcm,宽为ycm,
根据题意,得,
解这个方程组得:,
所以,矩形的面积为8×2=16×3=48cm2.
27.解:
∵b=++4,
∴a﹣3≥0且3﹣a≥0,
∴a=3,
∴b=4,
当a为等腰三角形的腰时,则此三角形周长为3+3+4=10,
当b为等腰三角形的腰时,则此三角形周长为4+4+3=11.
28.解:(1)由题意可得,
该空地的周长是:(+)×2=(9+8)×2≈(9×1.73+8×1.41)×2=53.7≈54(m),
即该空地的周长是54m;
(2)由题意可得,
绿化该空地所需的总费用是:=≈9×1.73×8×1.41×12≈2108(元),
答:绿化该空地所需的总费用是2108元.
