2021-2022学年冀教版数学八年级下册19.2平面直角坐标系 同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版数学八年级下册19.2平面直角坐标系 同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 205.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 07:18:19 | ||
图片预览



文档简介
冀教版数学八年级下册第十九章19.2平面直角坐标系
一、选择题
在平面直角坐标系中,点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
与平面直角坐标系中的点具有一一对应关系的是
A. 实数 B. 有理数 C. 有序实数对 D. 有序有理数对
直角坐标系中,、两点的横坐标相同但均不为零,则直线
A. 平行于轴 B. 平行于轴 C. 经过原点 D. 以上都不对
在平面直角坐标系中,点所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
一只跳蚤在第一象限及轴、轴上跳动,在第一秒钟,它从原点跳动到,然后接着按图中箭头所示方向跳动即,且每秒跳动一个单位,那么第秒时跳蚤所在位置的坐标是
A.
B.
C.
D.
已知点在轴上,点在轴上,则点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
下列坐标点在第四象限内的是
A. B. C. D.
点在轴上方,轴左侧,距离轴个单位长度,距离轴个单位长度,则点的坐标为
A. B. C. D.
在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,则点的坐标为
A. B. C. D.
若点在第四象限,且到轴的距离是,到轴的距离是,则点的坐标为
A. B. C. D.
二、填空题
在轴上,位于原点的下方,且距离原点个单位长度的点的坐标是_____.
平面直角坐标系中,点到原点的距离是______.
已知点在第四象限,则的取值范围是______.
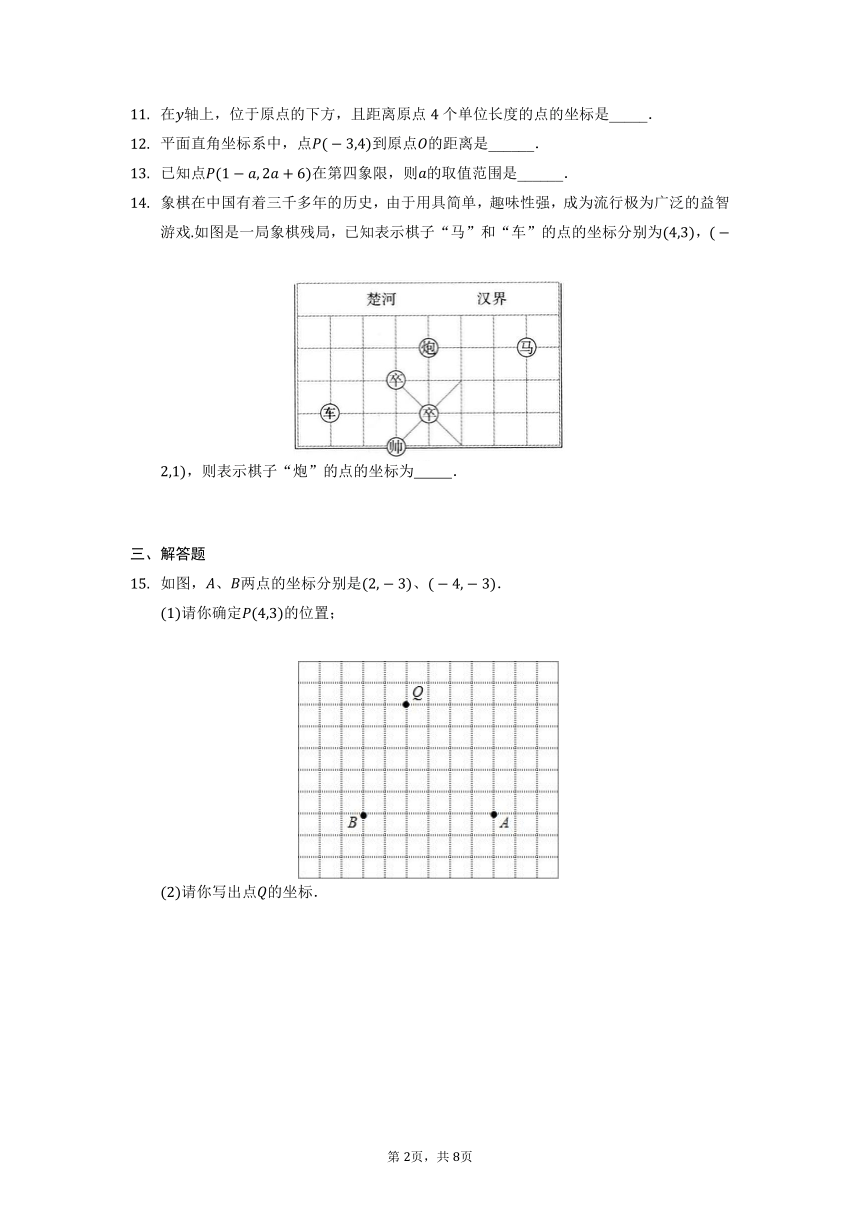
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏如图是一局象棋残局,已知表示棋子“马”和“车”的点的坐标分别为,,则表示棋子“炮”的点的坐标为 .
三、解答题
如图,、两点的坐标分别是、.
请你确定的位置;
请你写出点的坐标.
已知点,分别根据下列条件求出点的坐标.
点在轴上.
点到轴与轴的距离相等.
已知点.
若点在轴上,求的值.
若点到两坐标轴的距离相等,求点的坐标.
知当,都是实数,且满足时,称为“开心点”例如点为“开心点”.
因为当时,,,得,,
所以,,
所以.
所以是“开心点”.
判断点是否为“开心点”,并说明理由;
若点是“开心点”,请判断点在第几象限?并说明理由.
答案和解析
1.【答案】
【解析】解:根据点的坐标,横坐标为,纵坐标为,所以在第四象限.
故选D
2.【答案】
【解析】略
3.【答案】
【解析】解:直角坐标系下两个点的横坐标相同且不为零,
则说明这两点到轴的距离相等,且在轴的同一侧,
所以过这两点的直线平行于轴.
4.【答案】
【解析】解:点的横坐标,纵坐标,
点在第四象限.
5.【答案】
【解析】解:跳蚤运动的速度是每秒运动一个单位长度,
用的秒数分别是秒,秒,秒,
到用秒,
到用秒,
到用秒,
到用秒,
到用秒,
到用秒,
依此类推,到用秒.
故第秒时跳蚤所在位置的坐标是.
故选B.
6.【答案】
【解析】解:点在轴上,
,
解得,
点在轴上,
,
,
点的坐标为,
在第二象限.
故选B.
7.【答案】
【解析】解:由第四象限内的点的横坐标大于零,纵坐标小于零,得在第四象限内的是,
故选:.
根据第四象限内的点的横坐标大于零,纵坐标小于零,可得答案.
本题考查了点的坐标,熟记各象限内点的坐标特征是解题关键.
8.【答案】
【解析】解:点在轴上方,轴左侧,
点的纵坐标大于,横坐标小于,
点在第二象限.
点距离轴个单位长度,距离轴个单位长度,
点的横坐标是,纵坐标是,
故点的坐标为.
故选C.
9.【答案】
【解析】解:在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,
点的纵坐标为:,横坐标为:,
即点的坐标为:.
故选:.
10.【答案】
【解析】解:由到轴的距离是,到轴的距离是,得
,.
由点位于第四象限,得
则点坐标为,
故选:.
11.【答案】
【解析】解:点在轴上,位于原点的下方,
点在轴负半轴,
距离原点个单位长度,
点的坐标是.
故答案为.
12.【答案】
【解析】解:作轴于,则,.
则根据勾股定理,得.
故答案为.
13.【答案】
【解析点在第四象限,
解得.
故答案为.
14.【答案】
【解析】如图所示,表示棋子“炮”的点的坐标为.
15.【答案】解:根据、两点的坐标可知:轴平行于、两点所在的直线,且距离是;轴在距点距点位置处,如图建立直角坐标系,则点的位置,即如图所示的点;
点 的坐标是.
16.【答案】解:点在轴上,
,
解得:,
故,
则;
点到轴、轴的距离相等,
或,
解得:,,
故当时,,,
则;
故当时,,,
则.
综上所述:或.
17.【答案】解:点在轴上,
,
解得:;
点到两坐标轴的距离相等,
或
解得:或,
点的坐标为或.
18.【答案】解:不是“开心点”,理由如下,
当时,,,
解得,,
则,,
所以,
所以点不是“开心点”;
点在第三象限,
理由如下:
点是“开心点”,
,,
,,
代入有,
,,
,
故点在第三象限.
第2页,共2页
第1页,共1页
一、选择题
在平面直角坐标系中,点位于
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
与平面直角坐标系中的点具有一一对应关系的是
A. 实数 B. 有理数 C. 有序实数对 D. 有序有理数对
直角坐标系中,、两点的横坐标相同但均不为零,则直线
A. 平行于轴 B. 平行于轴 C. 经过原点 D. 以上都不对
在平面直角坐标系中,点所在的象限是
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
一只跳蚤在第一象限及轴、轴上跳动,在第一秒钟,它从原点跳动到,然后接着按图中箭头所示方向跳动即,且每秒跳动一个单位,那么第秒时跳蚤所在位置的坐标是
A.
B.
C.
D.
已知点在轴上,点在轴上,则点在
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
下列坐标点在第四象限内的是
A. B. C. D.
点在轴上方,轴左侧,距离轴个单位长度,距离轴个单位长度,则点的坐标为
A. B. C. D.
在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,则点的坐标为
A. B. C. D.
若点在第四象限,且到轴的距离是,到轴的距离是,则点的坐标为
A. B. C. D.
二、填空题
在轴上,位于原点的下方,且距离原点个单位长度的点的坐标是_____.
平面直角坐标系中,点到原点的距离是______.
已知点在第四象限,则的取值范围是______.
象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益智游戏如图是一局象棋残局,已知表示棋子“马”和“车”的点的坐标分别为,,则表示棋子“炮”的点的坐标为 .
三、解答题
如图,、两点的坐标分别是、.
请你确定的位置;
请你写出点的坐标.
已知点,分别根据下列条件求出点的坐标.
点在轴上.
点到轴与轴的距离相等.
已知点.
若点在轴上,求的值.
若点到两坐标轴的距离相等,求点的坐标.
知当,都是实数,且满足时,称为“开心点”例如点为“开心点”.
因为当时,,,得,,
所以,,
所以.
所以是“开心点”.
判断点是否为“开心点”,并说明理由;
若点是“开心点”,请判断点在第几象限?并说明理由.
答案和解析
1.【答案】
【解析】解:根据点的坐标,横坐标为,纵坐标为,所以在第四象限.
故选D
2.【答案】
【解析】略
3.【答案】
【解析】解:直角坐标系下两个点的横坐标相同且不为零,
则说明这两点到轴的距离相等,且在轴的同一侧,
所以过这两点的直线平行于轴.
4.【答案】
【解析】解:点的横坐标,纵坐标,
点在第四象限.
5.【答案】
【解析】解:跳蚤运动的速度是每秒运动一个单位长度,
用的秒数分别是秒,秒,秒,
到用秒,
到用秒,
到用秒,
到用秒,
到用秒,
到用秒,
依此类推,到用秒.
故第秒时跳蚤所在位置的坐标是.
故选B.
6.【答案】
【解析】解:点在轴上,
,
解得,
点在轴上,
,
,
点的坐标为,
在第二象限.
故选B.
7.【答案】
【解析】解:由第四象限内的点的横坐标大于零,纵坐标小于零,得在第四象限内的是,
故选:.
根据第四象限内的点的横坐标大于零,纵坐标小于零,可得答案.
本题考查了点的坐标,熟记各象限内点的坐标特征是解题关键.
8.【答案】
【解析】解:点在轴上方,轴左侧,
点的纵坐标大于,横坐标小于,
点在第二象限.
点距离轴个单位长度,距离轴个单位长度,
点的横坐标是,纵坐标是,
故点的坐标为.
故选C.
9.【答案】
【解析】解:在平面直角坐标系的第四象限内有一点,到轴的距离为,到轴的距离为,
点的纵坐标为:,横坐标为:,
即点的坐标为:.
故选:.
10.【答案】
【解析】解:由到轴的距离是,到轴的距离是,得
,.
由点位于第四象限,得
则点坐标为,
故选:.
11.【答案】
【解析】解:点在轴上,位于原点的下方,
点在轴负半轴,
距离原点个单位长度,
点的坐标是.
故答案为.
12.【答案】
【解析】解:作轴于,则,.
则根据勾股定理,得.
故答案为.
13.【答案】
【解析点在第四象限,
解得.
故答案为.
14.【答案】
【解析】如图所示,表示棋子“炮”的点的坐标为.
15.【答案】解:根据、两点的坐标可知:轴平行于、两点所在的直线,且距离是;轴在距点距点位置处,如图建立直角坐标系,则点的位置,即如图所示的点;
点 的坐标是.
16.【答案】解:点在轴上,
,
解得:,
故,
则;
点到轴、轴的距离相等,
或,
解得:,,
故当时,,,
则;
故当时,,,
则.
综上所述:或.
17.【答案】解:点在轴上,
,
解得:;
点到两坐标轴的距离相等,
或
解得:或,
点的坐标为或.
18.【答案】解:不是“开心点”,理由如下,
当时,,,
解得,,
则,,
所以,
所以点不是“开心点”;
点在第三象限,
理由如下:
点是“开心点”,
,,
,,
代入有,
,,
,
故点在第三象限.
第2页,共2页
第1页,共1页
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
