2021-2022学年湘教版九年级下册数学2.5.2圆的切线(一)课件(共14张PPT)
文档属性
| 名称 | 2021-2022学年湘教版九年级下册数学2.5.2圆的切线(一)课件(共14张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 432.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 09:42:27 | ||
图片预览






文档简介
(共14张PPT)
复习引入:
1、直线和圆有哪几种位置关系?
2、怎样判断直线和圆相切?
直线和圆的位置关系
第二课时 切线的判定
1、理解并掌握切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
学习目标
2、掌握判定圆的切线的两种证明方法。
自学指导:
阅读教材66-67的内容,并思考下列问题
1、阅读观察和完成探究部分,圆的切线判定定理是什么?怎样用几何语言表示?
2、完成做一做,怎样用三角板过圆上一点画圆的切线?
3、阅读例题2,思考判定圆的切线的方法有哪些?怎样运用它们证题?
经过半径的外端且垂直于这条半径
的直线是圆的切线。
条件:
(1)经过圆上的一点;
圆的切线判定定理:
(2)垂直于该点半径;
●O
┐
A
l
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
几何符号表达
1 判断题
1、经过半径外端的直线是圆的切线。( )
2、垂直于半径的直线是圆的切线。( )
5、和圆有公共点的直线是圆的切线。( )
6、和圆只有一个公共点的直线是圆的切线。( )
3、经过半径的一端并且垂直于这条半径的直线是圆的切线
( )
4、过直径的外端并且垂直于这条直径的直线是圆的切线。
( )
√
╳
╳
╳
╳
√
自学检测:
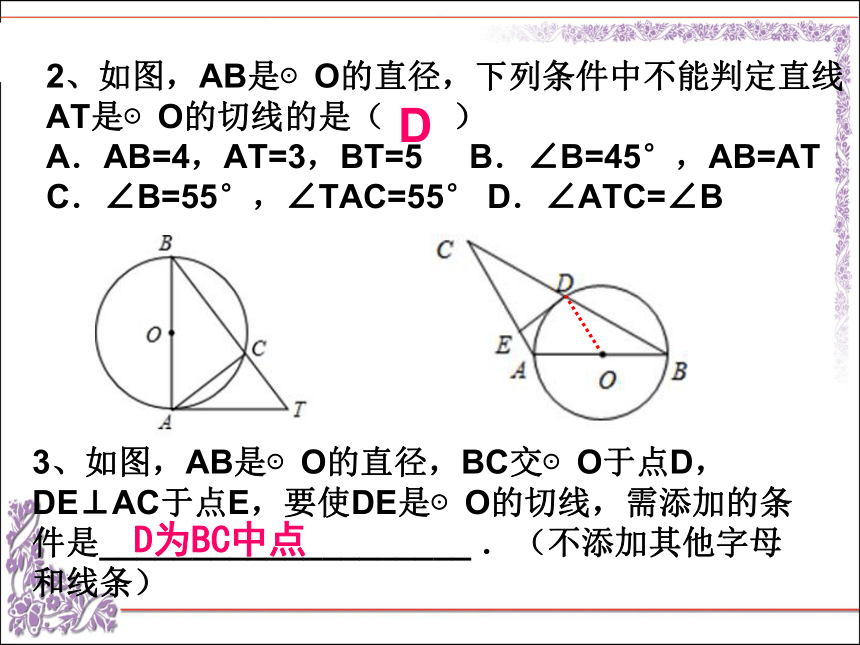
2、如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
A.AB=4,AT=3,BT=5 B.∠B=45°,AB=AT
C.∠B=55°,∠TAC=55° D.∠ATC=∠B
3、如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是____________________ .(不添加其他字母和线条)
D为BC中点
D
一展身手:
1、已知:如图,AB是⊙O的直径,P为⊙O外一点,PA⊥AB,弦BC∥OP
求证:PC是⊙O的切线.
证明:如图,连接OC;
∵BC∥OP,
∴∠B=∠POA,∠BCO=∠COP,
∵OB=OC,
∴∠B=∠OCB,
∴∠COP=∠AOP;
∵OC=OA,OP=OP,
∴△PCO≌△PAO,
∴∠OCP=∠OAP=90°,
∴PC是⊙O的切线.
方法:如果已知直线经过圆上一点,则连
结这点和圆心,得到辅助半径,再证所作半
径与这直线垂直。简记为:连半径,证垂直。
2、如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与AB相切于点D,求证AC与⊙O相切。
证明:连结OD,过点O作OE⊥AC于E点。
∵AB切⊙O于D ∴OD⊥AB
∴∠ODB=∠OEC=90°
又∵O是BC的中点 ∴OB=OC
∵AB=AC ∴∠B=∠C
∴△OBE≌△OCE
∴OE=OD,即OE是⊙O的半径
∴AC与⊙O相切
E
(2)如果已知条件中不知直线与圆是否有
公共点,则过圆心作直线的垂线段为辅助
线,再证垂线段长等于半径长。
简记为:作垂直,证半径。
挑战自我:
1、已知:如图,△ABC内接于⊙O,AB为直径,过点A作直线EF,要使得EF是⊙O的切线,还需添加的条件是(只需写出三种):
①__________________ 或
②_______________ 或
③__________________.
OA⊥EF
∠FAC=∠B
∠BAC+∠FAC=90°
并选其中一种加以证明。
2、在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
课堂小结
谈谈你这节课的收获?
要证切线看情况:公共点已知与未知,
1、圆的切线的判定方法?
2、圆的切线的证明方法?
已知公共点连半径证垂直,
未知公共点作垂直证半径。
当堂训练
1、已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900. 求证:CD是⊙O的切线.
A
C
B
D
0
2、如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
求证:CD是⊙O的切线;
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.
复习引入:
1、直线和圆有哪几种位置关系?
2、怎样判断直线和圆相切?
直线和圆的位置关系
第二课时 切线的判定
1、理解并掌握切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
学习目标
2、掌握判定圆的切线的两种证明方法。
自学指导:
阅读教材66-67的内容,并思考下列问题
1、阅读观察和完成探究部分,圆的切线判定定理是什么?怎样用几何语言表示?
2、完成做一做,怎样用三角板过圆上一点画圆的切线?
3、阅读例题2,思考判定圆的切线的方法有哪些?怎样运用它们证题?
经过半径的外端且垂直于这条半径
的直线是圆的切线。
条件:
(1)经过圆上的一点;
圆的切线判定定理:
(2)垂直于该点半径;
●O
┐
A
l
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
几何符号表达
1 判断题
1、经过半径外端的直线是圆的切线。( )
2、垂直于半径的直线是圆的切线。( )
5、和圆有公共点的直线是圆的切线。( )
6、和圆只有一个公共点的直线是圆的切线。( )
3、经过半径的一端并且垂直于这条半径的直线是圆的切线
( )
4、过直径的外端并且垂直于这条直径的直线是圆的切线。
( )
√
╳
╳
╳
╳
√
自学检测:
2、如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
A.AB=4,AT=3,BT=5 B.∠B=45°,AB=AT
C.∠B=55°,∠TAC=55° D.∠ATC=∠B
3、如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,需添加的条件是____________________ .(不添加其他字母和线条)
D为BC中点
D
一展身手:
1、已知:如图,AB是⊙O的直径,P为⊙O外一点,PA⊥AB,弦BC∥OP
求证:PC是⊙O的切线.
证明:如图,连接OC;
∵BC∥OP,
∴∠B=∠POA,∠BCO=∠COP,
∵OB=OC,
∴∠B=∠OCB,
∴∠COP=∠AOP;
∵OC=OA,OP=OP,
∴△PCO≌△PAO,
∴∠OCP=∠OAP=90°,
∴PC是⊙O的切线.
方法:如果已知直线经过圆上一点,则连
结这点和圆心,得到辅助半径,再证所作半
径与这直线垂直。简记为:连半径,证垂直。
2、如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与AB相切于点D,求证AC与⊙O相切。
证明:连结OD,过点O作OE⊥AC于E点。
∵AB切⊙O于D ∴OD⊥AB
∴∠ODB=∠OEC=90°
又∵O是BC的中点 ∴OB=OC
∵AB=AC ∴∠B=∠C
∴△OBE≌△OCE
∴OE=OD,即OE是⊙O的半径
∴AC与⊙O相切
E
(2)如果已知条件中不知直线与圆是否有
公共点,则过圆心作直线的垂线段为辅助
线,再证垂线段长等于半径长。
简记为:作垂直,证半径。
挑战自我:
1、已知:如图,△ABC内接于⊙O,AB为直径,过点A作直线EF,要使得EF是⊙O的切线,还需添加的条件是(只需写出三种):
①__________________ 或
②_______________ 或
③__________________.
OA⊥EF
∠FAC=∠B
∠BAC+∠FAC=90°
并选其中一种加以证明。
2、在Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径作⊙O交AC于点E,连结DE并延长,与BC的延长线交于点F.且BD=BF.
(1)求证:AC与⊙O相切.
(2)若BC=6,AB=12,求⊙O的面积.
课堂小结
谈谈你这节课的收获?
要证切线看情况:公共点已知与未知,
1、圆的切线的判定方法?
2、圆的切线的证明方法?
已知公共点连半径证垂直,
未知公共点作垂直证半径。
当堂训练
1、已知:如图,AC,BD与⊙O切于A、B,且AC∥BD,若∠COD=900. 求证:CD是⊙O的切线.
A
C
B
D
0
2、如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
求证:CD是⊙O的切线;
如图,AB是⊙O的直径,AD是⊙O的切线,点C在⊙O上,BC∥OD.
(1)若AB=2,OD=3,求BC的长;
(2)若作直线CD,试说明直线CD是⊙O的切线.
