2021-2022学年湘教版九年级数学下册2.2.2圆周角(一)课件 (共22张PPT)
文档属性
| 名称 | 2021-2022学年湘教版九年级数学下册2.2.2圆周角(一)课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 344.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 09:48:29 | ||
图片预览




文档简介
(共22张PPT)
1.圆心角的定义
.
O
B
C
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
创设情境 引入新课
九年级数学(下)第二章圆
2、2 圆周角(一)
学习目标:
1.掌握圆周角的概念
2.掌握圆周角定理并会灵活运用。
3.熟记圆周角定理的推论1,并会灵活运用。
自学指导:
1、阅读P49页的内容,什么叫做圆周角?
2、看P50—P51探究同弧所对的圆周角与圆心角之间的关系,并熟记定理;
3、阅读P51 “动脑筋”部分提出的问题,并熟记圆周角定理的推论1。
4.理解或尝试解答例题2
8分钟之后检测同学们的自学效果。
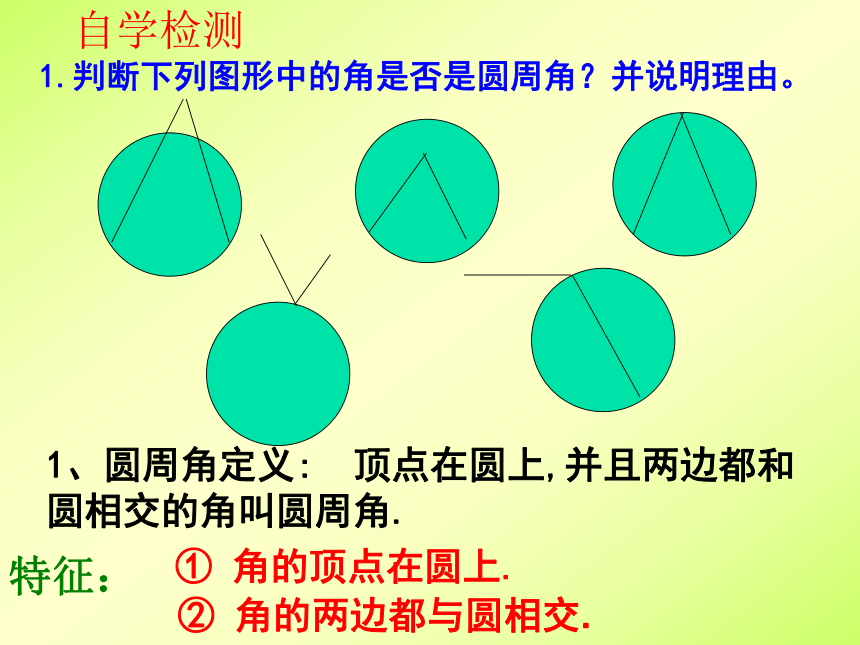
1.判断下列图形中的角是否是圆周角?并说明理由。
自学检测
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
A
B
C
O
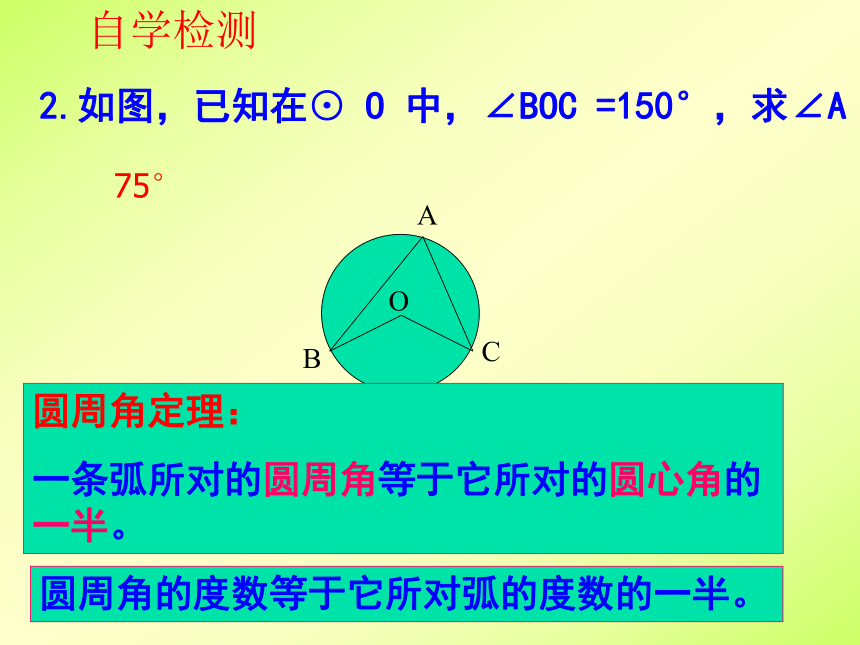
2.如图,已知在⊙ O 中,∠BOC =150°,求∠A
自学检测
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角的度数等于它所对弧的度数的一半。
75°
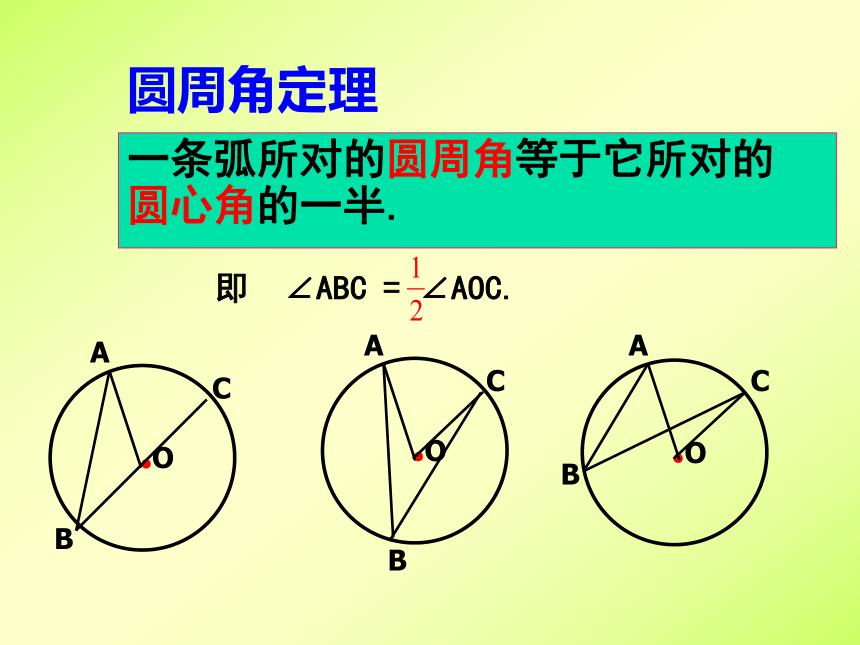
圆周角定理
一条弧所对的圆周角等于它所对的
圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
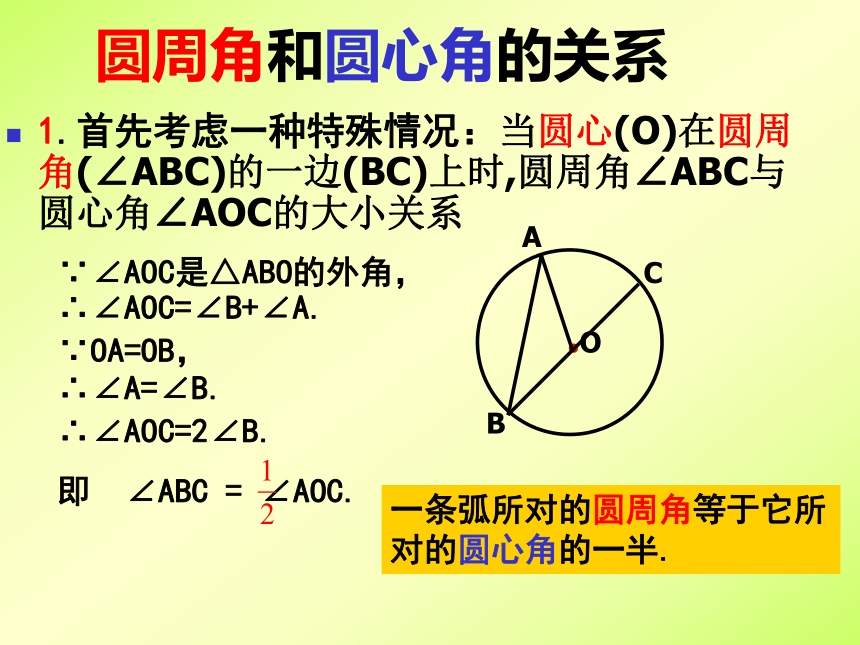
圆周角和圆心角的关系
1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
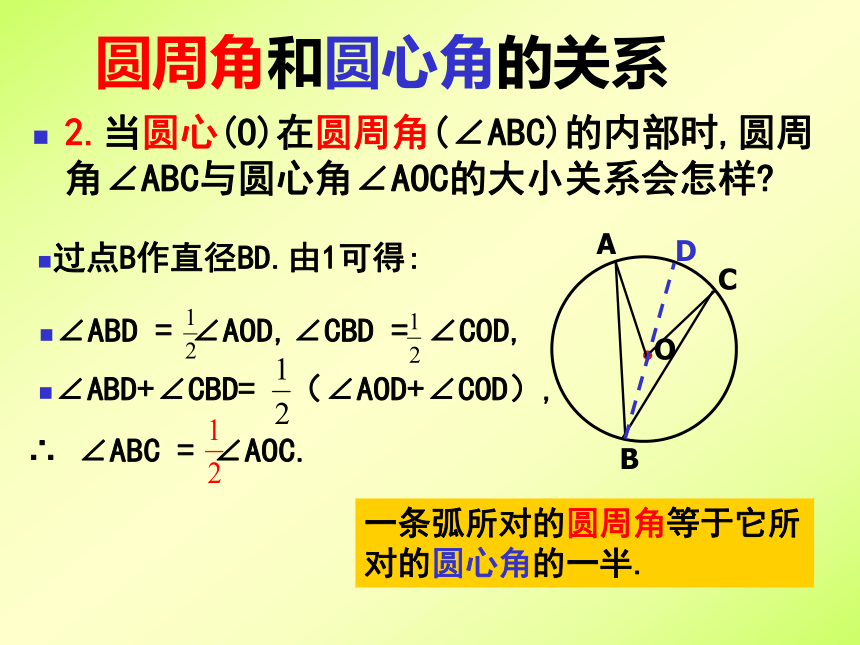
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
C
D
∠ABD = ∠AOD,∠CBD = ∠COD,
∠ABD+∠CBD= (∠AOD+∠COD),
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
∠ABD -∠CBD = (∠AOD-∠COD),
圆周角和圆心角的关系
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
自学检测
3.如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系
为什么
图1
∠B = ∠D= ∠E
●O
B
A
C
D
E
圆周角推论1
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
图中,若弧BD与弧DE相等,图中还有哪几个角相等?依据是什么?
4.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中
哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
方法点拨:由同弧来找相等的圆周角
图中有哪几对相似三角形?
△AEB∽△DEC
△AED∽△BEC
E
一展身手
1.如图,在⊙O中,∠BAC=32 ,则∠BOC=________。
2、如图,⊙O中,∠ACB = 130 ,则∠AOB=______。
3.一弦分圆周成两部分,其中一部分是
另一部分的4倍,则这弦所对的圆周角
度数为___。
A
O
C
B
A
O
C
B
36 或144
64
100
4、如图2,在⊙O中,弧AB=弧AC,若∠BOC=80°,
则∠ABC=______°.
70°
O
A
B
C
5.已知:OA、OB、OC都是⊙O的半径,
∠AOB=2∠BOC
求证:∠ACB= 2 ∠BAC
证明:
6.如图,P是△ABC的外接圆上的一点,
∠APC=∠CPB=60°。
求证:△ABC是等边三角形
·
·
A
P
B
C
O
挑战自我:
已知:如图,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.
课堂总结:
这节课我们都有什么收获?
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
3.推论1
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
当堂训练
必做题:
1.如图,弦AB与CD相交于点P,
求证:PA PB=PC PD
P
D
C
B
A
2.一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
选做题:
1、如图5,A、B、C、D是⊙O上四点,且点D是弧AB的中点,CD交OB于E,∠AOB=100°,∠OBC=55°,则∠OEC=______度.
2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AD=CB.
A
B
C
D
选做题:
课后思考:
已知:如图,△ABC内接于⊙O,AM平分∠BAC交⊙O于点M,AD⊥BC于D.
求证:∠MAO=∠MAD.
1.圆心角的定义
.
O
B
C
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
答:顶点在圆心的角叫圆心角
2.上节课我们学习了一个反映圆心角、弧、弦三个量之间关系的一个结论,这个结论是什么?
创设情境 引入新课
九年级数学(下)第二章圆
2、2 圆周角(一)
学习目标:
1.掌握圆周角的概念
2.掌握圆周角定理并会灵活运用。
3.熟记圆周角定理的推论1,并会灵活运用。
自学指导:
1、阅读P49页的内容,什么叫做圆周角?
2、看P50—P51探究同弧所对的圆周角与圆心角之间的关系,并熟记定理;
3、阅读P51 “动脑筋”部分提出的问题,并熟记圆周角定理的推论1。
4.理解或尝试解答例题2
8分钟之后检测同学们的自学效果。
1.判断下列图形中的角是否是圆周角?并说明理由。
自学检测
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
A
B
C
O
2.如图,已知在⊙ O 中,∠BOC =150°,求∠A
自学检测
圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角的度数等于它所对弧的度数的一半。
75°
圆周角定理
一条弧所对的圆周角等于它所对的
圆心角的一半.
●O
A
B
C
●O
A
B
C
●O
A
B
C
即 ∠ABC = ∠AOC.
圆周角和圆心角的关系
1.首先考虑一种特殊情况:当圆心(O)在圆周角(∠ABC)的一边(BC)上时,圆周角∠ABC与圆心角∠AOC的大小关系
∵∠AOC是△ABO的外角,
∴∠AOC=∠B+∠A.
∵OA=OB,
●O
A
B
C
∴∠A=∠B.
∴∠AOC=2∠B.
即 ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角和圆心角的关系
2.当圆心(O)在圆周角(∠ABC)的内部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
A
B
C
D
∠ABD = ∠AOD,∠CBD = ∠COD,
∠ABD+∠CBD= (∠AOD+∠COD),
过点B作直径BD.由1可得:
●O
∴ ∠ABC = ∠AOC.
一条弧所对的圆周角等于它所对的圆心角的一半.
D
∠ABD = ∠AOD,∠CBD = ∠COD,
A
B
C
∠ABD -∠CBD = (∠AOD-∠COD),
圆周角和圆心角的关系
3.当圆心(O)在圆周角(∠ABC)的外部时,圆周角∠ABC与圆心角∠AOC的大小关系会怎样
自学检测
3.如图1,在⊙O中,∠B,∠D,∠E的大小有什么关系
为什么
图1
∠B = ∠D= ∠E
●O
B
A
C
D
E
圆周角推论1
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
图中,若弧BD与弧DE相等,图中还有哪几个角相等?依据是什么?
4.如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中
哪些是相等的角?
A
B
C
D
1
2
3
4
5
6
7
8
∠1 = ∠4
∠5 = ∠8
∠2 = ∠7
∠3 = ∠6
方法点拨:由同弧来找相等的圆周角
图中有哪几对相似三角形?
△AEB∽△DEC
△AED∽△BEC
E
一展身手
1.如图,在⊙O中,∠BAC=32 ,则∠BOC=________。
2、如图,⊙O中,∠ACB = 130 ,则∠AOB=______。
3.一弦分圆周成两部分,其中一部分是
另一部分的4倍,则这弦所对的圆周角
度数为___。
A
O
C
B
A
O
C
B
36 或144
64
100
4、如图2,在⊙O中,弧AB=弧AC,若∠BOC=80°,
则∠ABC=______°.
70°
O
A
B
C
5.已知:OA、OB、OC都是⊙O的半径,
∠AOB=2∠BOC
求证:∠ACB= 2 ∠BAC
证明:
6.如图,P是△ABC的外接圆上的一点,
∠APC=∠CPB=60°。
求证:△ABC是等边三角形
·
·
A
P
B
C
O
挑战自我:
已知:如图,⊙O的直径AE=10cm,∠B=∠EAC.求AC的长.
课堂总结:
这节课我们都有什么收获?
1、圆周角定义: 顶点在圆上,并且两边都和圆相交的角叫圆周角.
2.圆周角定理:
一条弧所对的圆周角等于它所对的圆心角的一半。
3.推论1
同圆或等圆中,同弧或等弧所对的圆周角相等;
同圆或等圆中,相等的圆周角所对的弧也相等。
当堂训练
必做题:
1.如图,弦AB与CD相交于点P,
求证:PA PB=PC PD
P
D
C
B
A
2.一个圆形人工湖,弦AB是湖上的一座桥,已知桥AB长100m.测得圆周角∠C=45°求这个人工湖的直径.
A
B
C
选做题:
1、如图5,A、B、C、D是⊙O上四点,且点D是弧AB的中点,CD交OB于E,∠AOB=100°,∠OBC=55°,则∠OEC=______度.
2.已知:四边形ABCD内接于圆,BD平分∠ABC,且AB∥CD.求证:AD=CB.
A
B
C
D
选做题:
课后思考:
已知:如图,△ABC内接于⊙O,AM平分∠BAC交⊙O于点M,AD⊥BC于D.
求证:∠MAO=∠MAD.
