2021-2022学年北师大版八年级数学下册1.2直角三角形 同步自主提升训练 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册1.2直角三角形 同步自主提升训练 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 312.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 10:01:11 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学下册《1-2直角三角形》同步自主提升训练(附答案)
1.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.1 B.2 C.5 D.无法确定
2.如图,△ABC中,∠ACB=90°,∠B=30°,AC=1,过点C作CD1⊥AB于D1,过D1作D1D2⊥BC于D2,过D2作D2D3⊥AB于D3,这样继续作下去,…,线段DnDn+1等于(n为正整数)( )
A. B. C. D.
3.如图,在等边△ABC中,AB=6,∠AFB=90°,则CF的最小值为( )
A.3 B. C.6﹣3 D.3﹣3
4.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后,△CAP与△PQB全等.
5.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= cm.
6.如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= ,△ABC与△APQ全等.
7.已知Rt△ABC,AC=BC,点E、F在AB上,且∠ECF=45°,当AF BE=36时,△ABC的面积为 .
8.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为 .
9.如图所示,∠AOP=∠BOP=15°,PC∥OA交OB于C,PD⊥OA于D,若PC=4,则PD等于 .
10.如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于 .
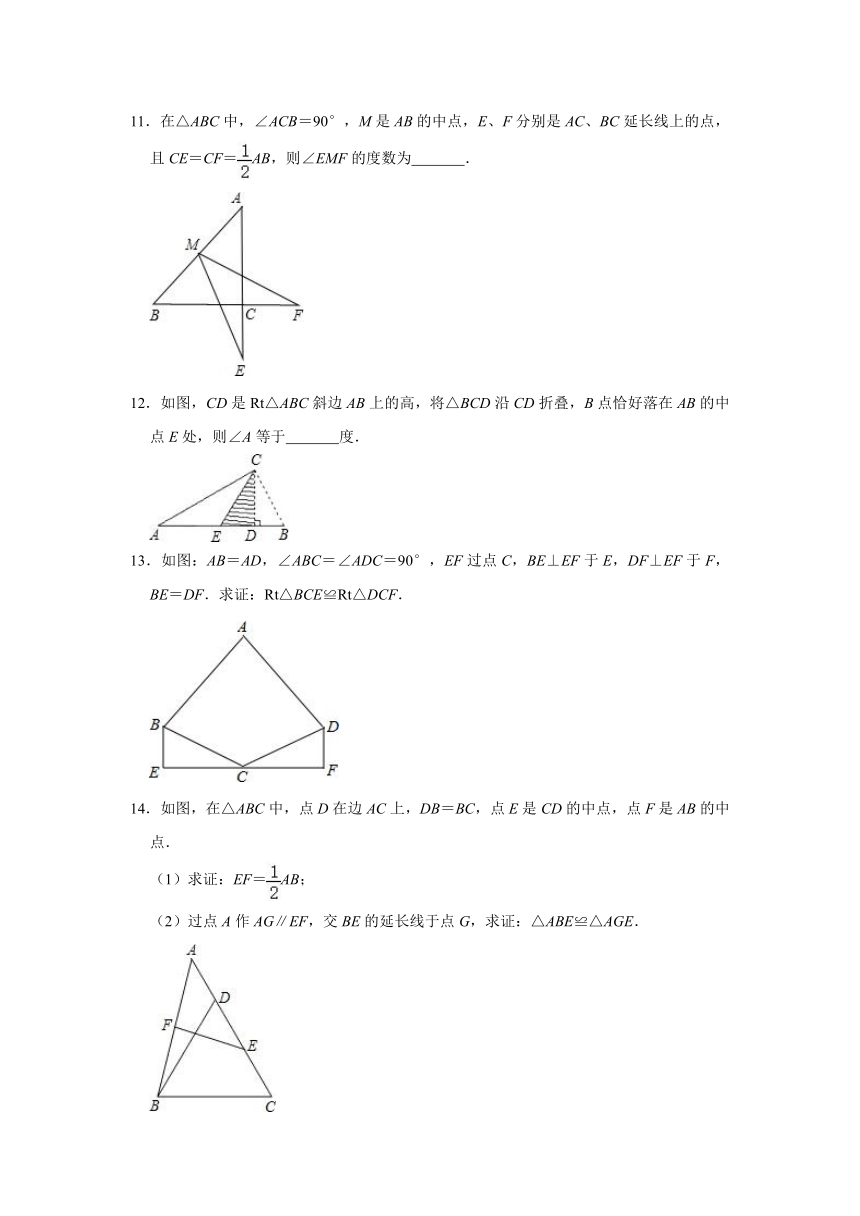
11.在△ABC中,∠ACB=90°,M是AB的中点,E、F分别是AC、BC延长线上的点,且CE=CF=AB,则∠EMF的度数为 .
12.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于 度.
13.如图:AB=AD,∠ABC=∠ADC=90°,EF过点C,BE⊥EF于E,DF⊥EF于F,BE=DF.求证:Rt△BCE≌Rt△DCF.
14.如图,在△ABC中,点D在边AC上,DB=BC,点E是CD的中点,点F是AB的中点.
(1)求证:EF=AB;
(2)过点A作AG∥EF,交BE的延长线于点G,求证:△ABE≌△AGE.
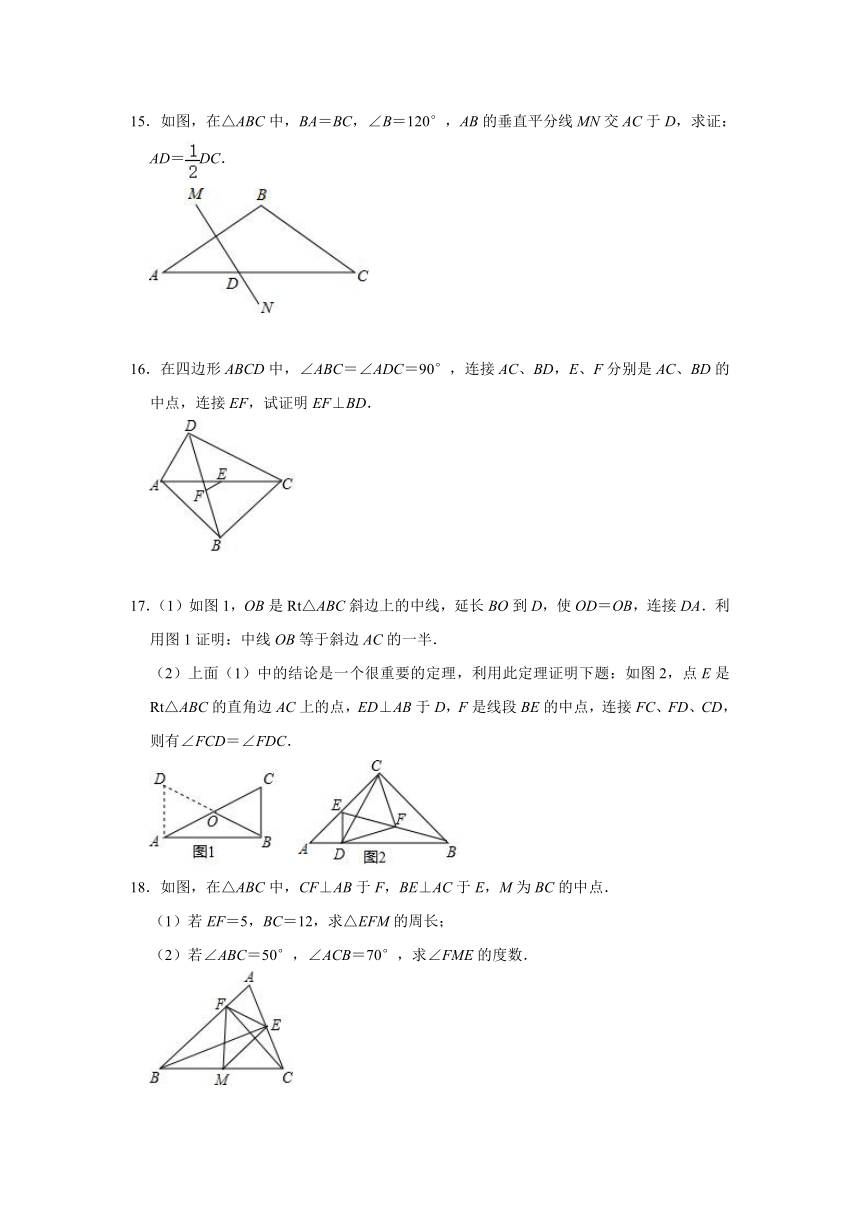
15.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD=DC.
16.在四边形ABCD中,∠ABC=∠ADC=90°,连接AC、BD,E、F分别是AC、BD的中点,连接EF,试证明EF⊥BD.
17.(1)如图1,OB是Rt△ABC斜边上的中线,延长BO到D,使OD=OB,连接DA.利用图1证明:中线OB等于斜边AC的一半.
(2)上面(1)中的结论是一个很重要的定理,利用此定理证明下题:如图2,点E是Rt△ABC的直角边AC上的点,ED⊥AB于D,F是线段BE的中点,连接FC、FD、CD,则有∠FCD=∠FDC.
18.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.
19.如图,在Rt△ABC中,∠ACB=90°,点D在边AC上(不与点A,C重合),DE⊥AB于点E,连接BD,F为BD的中点.
(1)若BD=10,求EF的长;
(2)写出图中的所有等腰三角形;
(3)试猜想∠A与∠CEF的关系并证明.
20.如图(1),已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
21.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,写出求BN长的思路.
22.已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD.
23.已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD.
24.已知:等边△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于O.求证:AO=2OD.
25.如图,三角形ABC中,AB=AC=2,∠B=15°,求AB边上的高.
26.如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD.
(1)求∠B的度数;
(2)求证:∠CAD=∠B.
27.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于D,CE⊥BD的延长线于点E.求证:.
28.如图,在直角△ABC中,D为斜边AB的中点,DE⊥DF,而E、F分别在AC和BC上,连接EF.观察AE、EF、BF能不能组成直角三角形.写出你的结论并说明理由.
参考答案
1.解:过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选:A.
2.解:∵△ABC中,∠ACB=90°,∠B=30°,CD1⊥AB,
∴∠ACD1=30°,CD1=,
同理,D1D2=()2,
…,
线段DnDn+1=()n+1.
故选:A.
3.解:如图取AB的中点E,连接EF、EC.
∵△ABC是等边三角形,AE=EB,
∴AB=BC=6,∠CBE=60°,
∴CE=BC sin60°=3,
∵∠AFB=90°,AE=EB,
∴EF=AB=3,
∴CF≥EC﹣EF,
∴当E、F、C共线时,FC的值最小,最小值为3﹣3,
故选:D.
4.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12(m)≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
5.解:∵在Rt△ABC中,∠BAC=90°,∠ADB=∠AEC=90°
∴∠BAD+∠EAC=90°,∠BAD+∠B=90°
∴∠EAC=∠B
∵AB=AC
∴△ABD≌△ACE(AAS)
∴AD=CE,BD=AE
∴DE=AD+AE=CE+BD=7cm.
故填7.
6.解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90°,
分两种情况:
①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在△ABC和△PQA中,,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=5或10时,△ABC与△APQ全等;
故答案为:5或10.
7.解:∵△ABC为等腰直角三角形,∴∠A=∠B=45°,
∴∠CEB=∠A+∠ACE=45°+∠ACE,∠ACF=∠ACE+∠ECF=∠ACE+45°,
∴∠CEB=∠ACF,
∴△ABC的面积=AC BC=×36=18.
故答案为:18.
8.解:由题意可得,BE平分∠ABC,DE=CE
又∠A=30°,AC=6
可得DE=AE
∴DE=(6﹣DE)
则DE=2.
故答案为2.
9.解:过点P作PM⊥OB于M,
∵PC∥OA,
∴∠COP=∠CPO=∠POD=15°,
∴∠BCP=30°,
∴PM=PC=2,
∵PD=PM,
∴PD=2.
故答案为:2.
10.解:如图,过C点作CE⊥OA,垂足为E,
∵PC∥OA,PD⊥OA,垂足为D,∴PD=CE,
∵∠AOB=60°,OC=4,
在Rt△OCE中,CE=2,
∴PD=CE=.
11.解:连接CM,
∵∠ACB=90°,M是AB的中点,
∴CM=AB,AM=BM=AB,
∵CE=CF=AB,
∴CE=MC,CF=MC,
∴∠1=∠E,∠2=∠F,
∵∠1+∠E=∠4,∠2+∠F=∠3,
∴∠1=∠4,∠2=∠3,
∴∠1+∠2=(∠4+∠3)=×90°=45°,
即:∠EMF=45°.
故答案为:45°.
12.解:∵在Rt△ABC中,CE是斜边AB的中线,
∴AE=CE,
∴∠A=∠ACE,
∵△CED是由△CBD折叠而成,
∴∠B=∠CED,
∵∠CEB=∠A+∠ACE=2∠A,
∴∠B=2∠A,
∵∠A+∠B=90°,
∴∠A=30°.
故答案为:30.
13.证明:方法一、
连接BD,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC=90°,
∴∠CBD=∠CDB,
∴BC=DC,
∵BE⊥EF,DF⊥EF,
∴∠E=∠F=90°,
在Rt△BCE和Rt△DCF中
,
∴Rt△BCE≌Rt△DCF(HL);
方法二、连接AC,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∵BE⊥EF,DF⊥EF,
∴∠BEC=∠DFC=90°,
在Rt△BCE和Rt△DCF中,
,
∴Rt△BCE≌Rt△DCF(HL).
14.证明:(1)连接BE,
∵DB=BC,点E是CD的中点,
∴BE⊥CD.
∵点F是Rt△ABE中斜边上的中点,
∴EF=;
(2)[方法一]在△ABG中,AF=BF,AG∥EF,
∴EF是△ABG的中位线,
∴BE=EG.
在△ABE和△AGE中,AE=AE,∠AEB=∠AEG=90°,
∴△ABE≌△AGE;
[方法二]由(1)得,EF=AF,
∴∠AEF=∠FAE.
∵EF∥AG,
∴∠AEF=∠EAG.
∴∠EAF=∠EAG.
∵AE=AE,∠AEB=∠AEG=90°,
∴△ABE≌△AGE.
15.解:如图,连接DB.
∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠ABD,
∵BA=BC,∠B=120°,
∴∠A=∠C=(180°﹣120°)=30°,
∴∠ABD=30°,
又∵∠ABC=120°,
∴∠DBC=120°﹣30°=90°,
∴BD=DC,
∴AD=DC.
16.证明:如图,连接BE、DE,
∵∠ABC=∠ADC=90°,E是AC的中点,
∴BE=DE=AC,
∵F是BD的中点,
∴EF⊥BD.
17.证明:(1)∵OB是Rt△ABC斜边上的中线,
∴OA=OC,
在△AOD和△COB中,
,
∴△AOD≌△COB(SAS),
∴AD=CB,∠DAO=∠C,
又∵∠BAC+∠C=90°,
∴∠BAC+∠DAO=90°,即∠DAB=90°=∠ABC,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
∴AC=BD,
又∵BO=BD,
∴BO=AC,即Rt△ABC中,中线OB等于斜边AC的一半.
(2)∵ED⊥AB,
∴∠EDB=90°=∠BCE,
又∵F是线段BE的中点,
∴Rt△BCE中,CF=BE,
Rt△BDE中,DF=BE,
∴CF=DF,
∴∠FCD=∠FDC.
18.解:(1)∵CF⊥AB于F,M为BC的中点,
∴ME=MC=BC=×12=6,
同理MF=MB=BC=×12=6,
∴△EFM的周长=6+6+5=17;
(2)∵MF=MB,
∴∠ABC=∠MFB=50°,
同理∠ACB=∠MEC=70°,
∴∠BMF=180°﹣50°﹣50°=80°,
∠EMC=180°﹣70°﹣70°=40°,
∴∠FME=180°﹣80°﹣40°=60°.
19.解:(1)∵DE⊥AB,F为BD的中点,
∴EF=BD=5;
(2)△DEF、△BEF、△DCF、△BCF、△CEF是等腰三角形;
(3)∠A=∠CEF.
证明:∵FE=FB,FC=FB,
∴∠FEB=∠FBE,∠FCB=∠FBC,
∴∠EFD=2∠EBF,∠CFD=2∠FBC,
∴∠CEF=×(180°﹣2∠EBF﹣2∠FBC)=90°﹣∠EBF﹣∠FBC,
又∠A=90°﹣∠EBF﹣∠FBC,
∴∠A=∠CEF.
20.(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=BC,ME=BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB),
=360°﹣2(∠ABC+∠ACB),
=360°﹣2(180°﹣∠A),
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连接DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC,
=2(180°﹣∠BAC),
=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC),
=2∠BAC﹣180°.
21.(1)证明:∵∠ABC=90°,M为AC中点,
∴BM=AC,
∵M为AC中点,N为DC中点,
∴MN=AD,
∵AD=AC,
∴BM=MN;
(2)解:∵∠BAD=60°,AC平分∠BAD,
∴∠DAC=∠CAB=30°,
∴BM=AM=AC=1,
∴∠MAB=∠MBA=30°,
∴∠CMB=60°
MN∥AD,MN=AD=1,
∴∠DAC=∠NMC=30°,
∴△NMB是等腰直角三角形,
由勾股定理得,BN==..
22.证明:如图,连接BE、DE,
∵∠ABC=90°,∠ADC=90°,点E是AC的中点,
∴BE=DE=AC,
∵点F是BD的中点,
∴EF⊥BD.
23.解:连接AE,DE,
∵∠BAC=∠BDC=90°,BE=EC,
∴AE=,DE=,
∴AE=DE,
在△AEF与△DEF中,
,
∴△AEF≌△DEF(SSS),
∴∠AFE=∠DFE=90°,
即EF⊥AD.
24.证明:∵等边△ABC中AD⊥BC,BE⊥AC,
∴∠BAE=60°,
∴2AE=AB,
同理可得:2BD=AB,2OD=OB,
在△AOE与△OBD中,
,
∴△AOE≌△OBD(AAS),
∴AO=OB,
∴AO=2OD.
25.解:过点C作BA的垂线,交BA的延长线于点D,
解:∵∠B=∠ACB=15°,
∴∠CAD=∠B+∠ACB=15°+15°=30°,
∵AC=2,CD是AB边上的高,
∴CD=AC=×2=1.
∴AB边上的高是1.
26.(1)解:∵∠BAD=15°,∠ADC=4∠BAD,
∴∠ADC=60°,
∴∠B=60°﹣15°=45°;
(2)证明:过C作CE⊥AD于E,连接EB.
∵∠ECD=90°﹣60°=30°
∴DC=2ED,
∵DC=2BD,
∴ED=BD,
∴∠DBE=∠DEB=∠ECD=30°,
∴∠EBA=45°﹣30°=15°=∠BAD,
∴AE=EC=EB,
∴∠CAD=∠ABD=45°.
27.解:延长CE、BA相交于点F.
∵∠EBF+∠F=90°,∠ACF+∠F=90°
∴∠EBF=∠ACF.
在△ABD和△ACF中
∴△ABD≌△ACF(ASA)
∴BD=CF
∵BD平分∠ABC,
∴∠CBE=∠FBE,
∴在△BCE和△BFE中
,
∴△BCE≌△BFE(ASA)
∴CE=EF
∴.
28.解:如图,延长FD到F′,使DF′=DF,连接AF′、EF′,
∵D为斜边AB的中点,
∴AD=BD,
在△ADF′和△BDF中,
,
∴△ADF′≌△BDF(SAS),
∴AF′=BF,∠B=∠DAF′,
∵∠BAC+∠B=90°,
∴∠BAC+∠DAF′=∠BAC+∠B=90°,
即∠EAF′=90°,
又∵DE⊥DF,
∴EF′=EF,
∴△EAF′是以EF′为斜边的直角三角形,
故AE、EF、BF能组成直角三角形,斜边为EF.
1.已知如图,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( )
A.1 B.2 C.5 D.无法确定
2.如图,△ABC中,∠ACB=90°,∠B=30°,AC=1,过点C作CD1⊥AB于D1,过D1作D1D2⊥BC于D2,过D2作D2D3⊥AB于D3,这样继续作下去,…,线段DnDn+1等于(n为正整数)( )
A. B. C. D.
3.如图,在等边△ABC中,AB=6,∠AFB=90°,则CF的最小值为( )
A.3 B. C.6﹣3 D.3﹣3
4.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后,△CAP与△PQB全等.
5.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= cm.
6.如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP= ,△ABC与△APQ全等.
7.已知Rt△ABC,AC=BC,点E、F在AB上,且∠ECF=45°,当AF BE=36时,△ABC的面积为 .
8.如图,已知Rt△ABC中,∠C=90°,∠A=30°,AC=6.沿DE折叠,使得点A与点B重合,则折痕DE的长为 .
9.如图所示,∠AOP=∠BOP=15°,PC∥OA交OB于C,PD⊥OA于D,若PC=4,则PD等于 .
10.如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C.若∠AOB=60°,OC=4,则点P到OA的距离PD等于 .
11.在△ABC中,∠ACB=90°,M是AB的中点,E、F分别是AC、BC延长线上的点,且CE=CF=AB,则∠EMF的度数为 .
12.如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于 度.
13.如图:AB=AD,∠ABC=∠ADC=90°,EF过点C,BE⊥EF于E,DF⊥EF于F,BE=DF.求证:Rt△BCE≌Rt△DCF.
14.如图,在△ABC中,点D在边AC上,DB=BC,点E是CD的中点,点F是AB的中点.
(1)求证:EF=AB;
(2)过点A作AG∥EF,交BE的延长线于点G,求证:△ABE≌△AGE.
15.如图,在△ABC中,BA=BC,∠B=120°,AB的垂直平分线MN交AC于D,求证:AD=DC.
16.在四边形ABCD中,∠ABC=∠ADC=90°,连接AC、BD,E、F分别是AC、BD的中点,连接EF,试证明EF⊥BD.
17.(1)如图1,OB是Rt△ABC斜边上的中线,延长BO到D,使OD=OB,连接DA.利用图1证明:中线OB等于斜边AC的一半.
(2)上面(1)中的结论是一个很重要的定理,利用此定理证明下题:如图2,点E是Rt△ABC的直角边AC上的点,ED⊥AB于D,F是线段BE的中点,连接FC、FD、CD,则有∠FCD=∠FDC.
18.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点.
(1)若EF=5,BC=12,求△EFM的周长;
(2)若∠ABC=50°,∠ACB=70°,求∠FME的度数.
19.如图,在Rt△ABC中,∠ACB=90°,点D在边AC上(不与点A,C重合),DE⊥AB于点E,连接BD,F为BD的中点.
(1)若BD=10,求EF的长;
(2)写出图中的所有等腰三角形;
(3)试猜想∠A与∠CEF的关系并证明.
20.如图(1),已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M、N分别是线段BC、DE的中点.
(1)求证:MN⊥DE.
(2)连接DM,ME,猜想∠A与∠DME之间的关系,并证明猜想.
(3)当∠A变为钝角时,如图(2),上述(1)(2)中的结论是否都成立,若结论成立,直接回答,不需证明;若结论不成立,说明理由.
21.如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,CD的中点,连接BM,MN,BN.
(1)求证:BM=MN;
(2)若∠BAD=60°,AC平分∠BAD,AC=2,写出求BN长的思路.
22.已知:如图,四边形ABCD中,∠ABC=90°,∠ADC=90°,点E为AC中点,点F为BD中点.求证:EF⊥BD.
23.已知:如图,∠BAC=∠BDC=90°,点E在BC上,点F在AD上,BE=EC,AF=FD.求证:EF⊥AD.
24.已知:等边△ABC中,AD⊥BC,BE⊥AC,垂足分别为点D、E,AD与BE交于O.求证:AO=2OD.
25.如图,三角形ABC中,AB=AC=2,∠B=15°,求AB边上的高.
26.如图,在△ABC中,AD交边BC于点D,∠BAD=15°,∠ADC=4∠BAD,DC=2BD.
(1)求∠B的度数;
(2)求证:∠CAD=∠B.
27.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于D,CE⊥BD的延长线于点E.求证:.
28.如图,在直角△ABC中,D为斜边AB的中点,DE⊥DF,而E、F分别在AC和BC上,连接EF.观察AE、EF、BF能不能组成直角三角形.写出你的结论并说明理由.
参考答案
1.解:过D作BC的垂线交BC于G,过E作AD的垂线交AD的延长线于F,
∵∠EDF+∠FDC=90°,
∠GDC+∠FDC=90°,
∴∠EDF=∠GDC,
于是在Rt△EDF和Rt△CDG中,
,
∴△DEF≌△DCG,
∴EF=CG=BC﹣BG=BC﹣AD=3﹣2=1,
所以,S△ADE=(AD×EF)÷2=(2×1)÷2=1.
故选:A.
2.解:∵△ABC中,∠ACB=90°,∠B=30°,CD1⊥AB,
∴∠ACD1=30°,CD1=,
同理,D1D2=()2,
…,
线段DnDn+1=()n+1.
故选:A.
3.解:如图取AB的中点E,连接EF、EC.
∵△ABC是等边三角形,AE=EB,
∴AB=BC=6,∠CBE=60°,
∴CE=BC sin60°=3,
∵∠AFB=90°,AE=EB,
∴EF=AB=3,
∴CF≥EC﹣EF,
∴当E、F、C共线时,FC的值最小,最小值为3﹣3,
故选:D.
4.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12(m)≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
5.解:∵在Rt△ABC中,∠BAC=90°,∠ADB=∠AEC=90°
∴∠BAD+∠EAC=90°,∠BAD+∠B=90°
∴∠EAC=∠B
∵AB=AC
∴△ABD≌△ACE(AAS)
∴AD=CE,BD=AE
∴DE=AD+AE=CE+BD=7cm.
故填7.
6.解:∵AX⊥AC,
∴∠PAQ=90°,
∴∠C=∠PAQ=90°,
分两种情况:
①当AP=BC=5时,
在Rt△ABC和Rt△QPA中,,
∴Rt△ABC≌Rt△QPA(HL);
②当AP=CA=10时,
在△ABC和△PQA中,,
∴Rt△ABC≌Rt△PQA(HL);
综上所述:当点P运动到AP=5或10时,△ABC与△APQ全等;
故答案为:5或10.
7.解:∵△ABC为等腰直角三角形,∴∠A=∠B=45°,
∴∠CEB=∠A+∠ACE=45°+∠ACE,∠ACF=∠ACE+∠ECF=∠ACE+45°,
∴∠CEB=∠ACF,
∴△ABC的面积=AC BC=×36=18.
故答案为:18.
8.解:由题意可得,BE平分∠ABC,DE=CE
又∠A=30°,AC=6
可得DE=AE
∴DE=(6﹣DE)
则DE=2.
故答案为2.
9.解:过点P作PM⊥OB于M,
∵PC∥OA,
∴∠COP=∠CPO=∠POD=15°,
∴∠BCP=30°,
∴PM=PC=2,
∵PD=PM,
∴PD=2.
故答案为:2.
10.解:如图,过C点作CE⊥OA,垂足为E,
∵PC∥OA,PD⊥OA,垂足为D,∴PD=CE,
∵∠AOB=60°,OC=4,
在Rt△OCE中,CE=2,
∴PD=CE=.
11.解:连接CM,
∵∠ACB=90°,M是AB的中点,
∴CM=AB,AM=BM=AB,
∵CE=CF=AB,
∴CE=MC,CF=MC,
∴∠1=∠E,∠2=∠F,
∵∠1+∠E=∠4,∠2+∠F=∠3,
∴∠1=∠4,∠2=∠3,
∴∠1+∠2=(∠4+∠3)=×90°=45°,
即:∠EMF=45°.
故答案为:45°.
12.解:∵在Rt△ABC中,CE是斜边AB的中线,
∴AE=CE,
∴∠A=∠ACE,
∵△CED是由△CBD折叠而成,
∴∠B=∠CED,
∵∠CEB=∠A+∠ACE=2∠A,
∴∠B=2∠A,
∵∠A+∠B=90°,
∴∠A=30°.
故答案为:30.
13.证明:方法一、
连接BD,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ABC=∠ADC=90°,
∴∠CBD=∠CDB,
∴BC=DC,
∵BE⊥EF,DF⊥EF,
∴∠E=∠F=90°,
在Rt△BCE和Rt△DCF中
,
∴Rt△BCE≌Rt△DCF(HL);
方法二、连接AC,
在Rt△ABC和Rt△ADC中,
,
∴Rt△ABC≌Rt△ADC(HL),
∵BE⊥EF,DF⊥EF,
∴∠BEC=∠DFC=90°,
在Rt△BCE和Rt△DCF中,
,
∴Rt△BCE≌Rt△DCF(HL).
14.证明:(1)连接BE,
∵DB=BC,点E是CD的中点,
∴BE⊥CD.
∵点F是Rt△ABE中斜边上的中点,
∴EF=;
(2)[方法一]在△ABG中,AF=BF,AG∥EF,
∴EF是△ABG的中位线,
∴BE=EG.
在△ABE和△AGE中,AE=AE,∠AEB=∠AEG=90°,
∴△ABE≌△AGE;
[方法二]由(1)得,EF=AF,
∴∠AEF=∠FAE.
∵EF∥AG,
∴∠AEF=∠EAG.
∴∠EAF=∠EAG.
∵AE=AE,∠AEB=∠AEG=90°,
∴△ABE≌△AGE.
15.解:如图,连接DB.
∵MN是AB的垂直平分线,
∴AD=DB,
∴∠A=∠ABD,
∵BA=BC,∠B=120°,
∴∠A=∠C=(180°﹣120°)=30°,
∴∠ABD=30°,
又∵∠ABC=120°,
∴∠DBC=120°﹣30°=90°,
∴BD=DC,
∴AD=DC.
16.证明:如图,连接BE、DE,
∵∠ABC=∠ADC=90°,E是AC的中点,
∴BE=DE=AC,
∵F是BD的中点,
∴EF⊥BD.
17.证明:(1)∵OB是Rt△ABC斜边上的中线,
∴OA=OC,
在△AOD和△COB中,
,
∴△AOD≌△COB(SAS),
∴AD=CB,∠DAO=∠C,
又∵∠BAC+∠C=90°,
∴∠BAC+∠DAO=90°,即∠DAB=90°=∠ABC,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS),
∴AC=BD,
又∵BO=BD,
∴BO=AC,即Rt△ABC中,中线OB等于斜边AC的一半.
(2)∵ED⊥AB,
∴∠EDB=90°=∠BCE,
又∵F是线段BE的中点,
∴Rt△BCE中,CF=BE,
Rt△BDE中,DF=BE,
∴CF=DF,
∴∠FCD=∠FDC.
18.解:(1)∵CF⊥AB于F,M为BC的中点,
∴ME=MC=BC=×12=6,
同理MF=MB=BC=×12=6,
∴△EFM的周长=6+6+5=17;
(2)∵MF=MB,
∴∠ABC=∠MFB=50°,
同理∠ACB=∠MEC=70°,
∴∠BMF=180°﹣50°﹣50°=80°,
∠EMC=180°﹣70°﹣70°=40°,
∴∠FME=180°﹣80°﹣40°=60°.
19.解:(1)∵DE⊥AB,F为BD的中点,
∴EF=BD=5;
(2)△DEF、△BEF、△DCF、△BCF、△CEF是等腰三角形;
(3)∠A=∠CEF.
证明:∵FE=FB,FC=FB,
∴∠FEB=∠FBE,∠FCB=∠FBC,
∴∠EFD=2∠EBF,∠CFD=2∠FBC,
∴∠CEF=×(180°﹣2∠EBF﹣2∠FBC)=90°﹣∠EBF﹣∠FBC,
又∠A=90°﹣∠EBF﹣∠FBC,
∴∠A=∠CEF.
20.(1)证明:如图(1),连接DM,ME,
∵CD、BE分别是AB、AC边上的高,M是BC的中点,
∴DM=BC,ME=BC,
∴DM=ME,
又∵N为DE中点,
∴MN⊥DE;
(2)在△ABC中,∠ABC+∠ACB=180°﹣∠A,
∵DM=ME=BM=MC,
∴∠BMD+∠CME=(180°﹣2∠ABC)+(180°﹣2∠ACB),
=360°﹣2(∠ABC+∠ACB),
=360°﹣2(180°﹣∠A),
=2∠A,
∴∠DME=180°﹣2∠A;
(3)结论(1)成立,结论(2)不成立,
理由如下:连接DM,ME,
在△ABC中,∠ABC+∠ACB=180°﹣∠BAC,
∵DM=ME=BM=MC,
∴∠BME+∠CMD=2∠ACB+2∠ABC,
=2(180°﹣∠BAC),
=360°﹣2∠BAC,
∴∠DME=180°﹣(360°﹣2∠BAC),
=2∠BAC﹣180°.
21.(1)证明:∵∠ABC=90°,M为AC中点,
∴BM=AC,
∵M为AC中点,N为DC中点,
∴MN=AD,
∵AD=AC,
∴BM=MN;
(2)解:∵∠BAD=60°,AC平分∠BAD,
∴∠DAC=∠CAB=30°,
∴BM=AM=AC=1,
∴∠MAB=∠MBA=30°,
∴∠CMB=60°
MN∥AD,MN=AD=1,
∴∠DAC=∠NMC=30°,
∴△NMB是等腰直角三角形,
由勾股定理得,BN==..
22.证明:如图,连接BE、DE,
∵∠ABC=90°,∠ADC=90°,点E是AC的中点,
∴BE=DE=AC,
∵点F是BD的中点,
∴EF⊥BD.
23.解:连接AE,DE,
∵∠BAC=∠BDC=90°,BE=EC,
∴AE=,DE=,
∴AE=DE,
在△AEF与△DEF中,
,
∴△AEF≌△DEF(SSS),
∴∠AFE=∠DFE=90°,
即EF⊥AD.
24.证明:∵等边△ABC中AD⊥BC,BE⊥AC,
∴∠BAE=60°,
∴2AE=AB,
同理可得:2BD=AB,2OD=OB,
在△AOE与△OBD中,
,
∴△AOE≌△OBD(AAS),
∴AO=OB,
∴AO=2OD.
25.解:过点C作BA的垂线,交BA的延长线于点D,
解:∵∠B=∠ACB=15°,
∴∠CAD=∠B+∠ACB=15°+15°=30°,
∵AC=2,CD是AB边上的高,
∴CD=AC=×2=1.
∴AB边上的高是1.
26.(1)解:∵∠BAD=15°,∠ADC=4∠BAD,
∴∠ADC=60°,
∴∠B=60°﹣15°=45°;
(2)证明:过C作CE⊥AD于E,连接EB.
∵∠ECD=90°﹣60°=30°
∴DC=2ED,
∵DC=2BD,
∴ED=BD,
∴∠DBE=∠DEB=∠ECD=30°,
∴∠EBA=45°﹣30°=15°=∠BAD,
∴AE=EC=EB,
∴∠CAD=∠ABD=45°.
27.解:延长CE、BA相交于点F.
∵∠EBF+∠F=90°,∠ACF+∠F=90°
∴∠EBF=∠ACF.
在△ABD和△ACF中
∴△ABD≌△ACF(ASA)
∴BD=CF
∵BD平分∠ABC,
∴∠CBE=∠FBE,
∴在△BCE和△BFE中
,
∴△BCE≌△BFE(ASA)
∴CE=EF
∴.
28.解:如图,延长FD到F′,使DF′=DF,连接AF′、EF′,
∵D为斜边AB的中点,
∴AD=BD,
在△ADF′和△BDF中,
,
∴△ADF′≌△BDF(SAS),
∴AF′=BF,∠B=∠DAF′,
∵∠BAC+∠B=90°,
∴∠BAC+∠DAF′=∠BAC+∠B=90°,
即∠EAF′=90°,
又∵DE⊥DF,
∴EF′=EF,
∴△EAF′是以EF′为斜边的直角三角形,
故AE、EF、BF能组成直角三角形,斜边为EF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
