22021-2022学年北师大版九年级数学下册2.4.1二次函数的应用同步练习 (word版含答案)
文档属性
| 名称 | 22021-2022学年北师大版九年级数学下册2.4.1二次函数的应用同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 226.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 10:11:35 | ||
图片预览



文档简介
2.4.1二次函数的应用
1.(舟山)当时,二次函数有最大值4,则实数的值为( )
A. B. 或 C. 2或 D. 2或或
2. 已知0≤x≤,那么函数y=-2x2+8x-6的最大值是( )
A. -10.5 B. 2 C. -2.5 D. -6
3. 若二次函数y=x2-2x+c的图象与y轴的交点为(0,-3),则此二次函数有( )
A. 最小值-2 B. 最小值-3 C. 最小值-4 D. 最大值-4
4. 下列四个说法中正确的是( )
①已知反比例函数y=,则当y≤时自变量x的取值范围是x≥4;
②点(x1,y1)和点(x2,y2)在反比例函数y=-的图象上,若x1<x2,则y1<y2;
③二次函数y=2x2+8x+13(-3≤x≤0)的最大值为13,最小值为7;
④已知函数y=x2+mx+1的图象,当x≤时,y随着x的增大而减小,则m=-。
A. ④ B. ①② C. ③④ D. 四个说法都不对
5. 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与射线AC相交于点D。当△ODA是等边三角形时,这两个二次函数的最大值之和等于( )
A. B. C. 2 D.
6. 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 。
7. 如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF。则AF的最小值是 。
8. 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP。
(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值;
(3)在Rt△ABC中,两条直角边BC、AC满足关系式BC=λAC,是否存在一个λ的值,使Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等。
9.如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
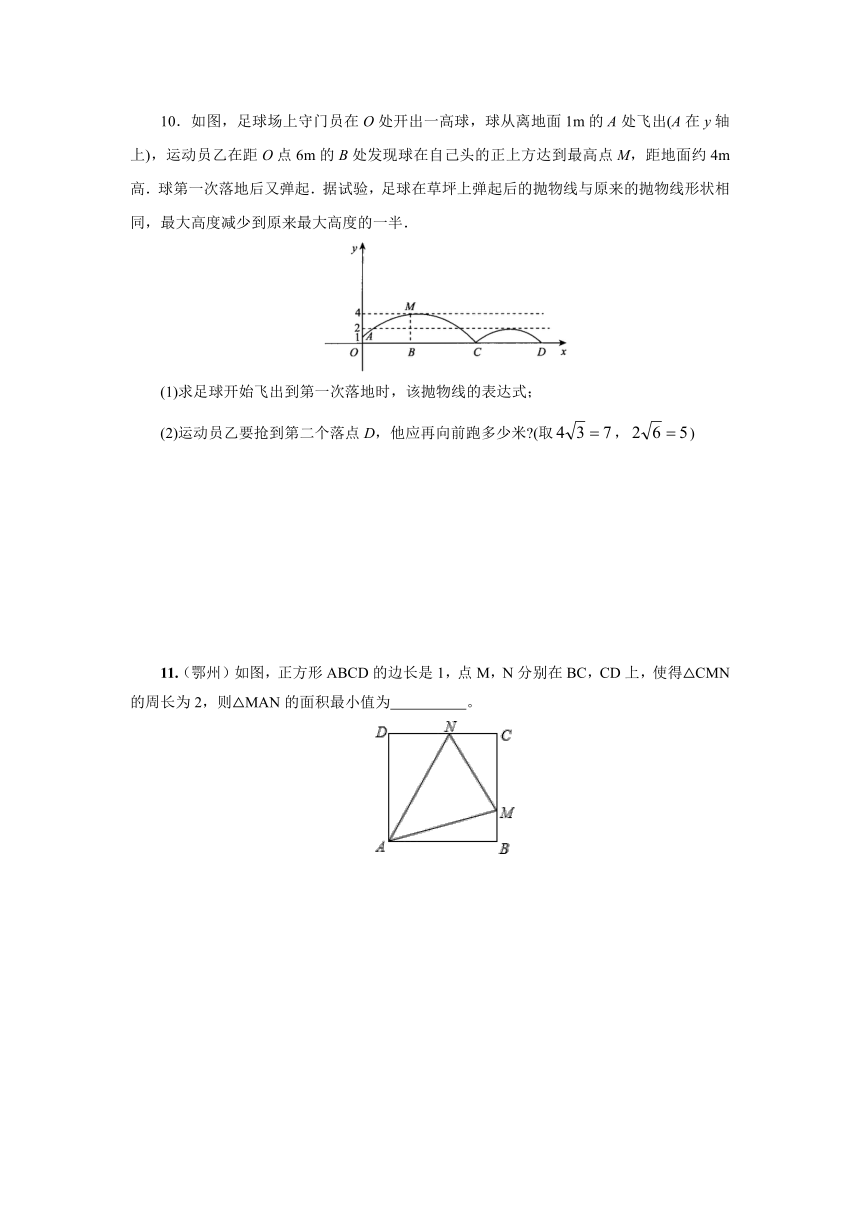
10.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米 (取,)
11.(鄂州)如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为 。
12.(绍兴)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm。要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。问加工成的正方形零件的边长是多少毫米?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题。
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1所示,此时,这个矩形零件的两条边长又分别为多少毫米?请你计算。
(2)如果原题中所要加工的零件只是一个矩形,如图2所示,这样,此矩形零件的两条边长就不能确定,但这个矩形的面积有最大值,求达到这个最大值时矩形零件的两条边长。
参考答案
1.解:二次函数的对称轴为直线,
①当,时,二次函数有最大值,
此时,,
解得,与矛盾,故值不存在;
②当,时,二次函数有最大值,
此时,,
解得(舍去),符合题意;
③当,时,二次函数有最大值,
此时,,
解得,
综上所述,的值为2或。故选C。
2. C 解析:∵y=-2x2+8x-6=-2(x-2)2+2,
∴该抛物线的对称轴是x=2,且在x<2上y随x的增大而增大。
又∵0≤x≤,∴当x=时,y取最大值,y最大=-2(-2)2+2=-2.5。
故选C。
3. C 解析:∵二次函数y=x2-2x+c的图象与y轴的交点为(0,-3),
∴c=-3,∴二次函数解析式为y=x2-2x-3,
∵y=x2-2x-3=(x-1)2-4,∴此二次函数当x=1时,有最小值-4。
故选C。
4. D 解析:①因为反比例函数y=,k=6的函数图象在一、三象限,
在第一象限内x≥4时,y≤;
在第三象限内所有的函数值都小于,即x<0。所以不正确。
②因为k=-<0,所以函数图象位于二、四象限内,
当x1、x2位于不同的象限内时,则不成立。
③因为a=2>0,所以函数图象开口向上,
当x= = = 2时,函数有最小值==5,所以不正确。
④因为a=>0,所以函数图象开口向上,
当x≤-时,y随x的增大而减小,
即x≤ m,所以 m≥,即m≤ ,不正确。
故选D。
5. C 解析:如图,连接PB、PC,由二次函数的性质,OB=PB,PC=AC,
∵△ODA是等边三角形,
∴∠AOD=∠OAD=60°,∴△POB和△ACP是等边三角形,
∵A(4,0),∴OA=4,∴点B、C的纵坐标之和为4×=2,
即两个二次函数的最大值之和等于2。故选C。
6. 6 解析:∵y=-x2+x+2,∴当y=0时,-x2+x+2=0,即-(x-2)(x+1)=0,解得 x=2或x=-1
因为P为第一象限点,
故设P(x,y)(0<x<2,y>0),
∴C=2(x+y)=2(x-x2+x+2)=-2(x-1)2+6,
∴当x=1时,C最大值=6,
即四边形OAPB周长的最大值为6,
7. 5 解析:设BE=x,则EC=4-x,
∵AE⊥EF,∴∠AEF=90°,∴∠AEB+∠FEC=90°,
而∠AEB+∠BAE=90°,∴∠BAE=∠FEC,∴Rt△ABE∽Rt△ECF,
∴=,即=,解得FC=,
∴DF=4-FC=4-=x2-x+4=(x-2)2+3
当x=2时,DF有最小值3,
∵AF2=AD2+DF2,∴AF的最小值为5。
8. 解:(1)不论点P在BC边上何处时,都有∠PQB=∠C=90°,∠B=∠B,
∴△PBQ∽△ABC;
(2)设BP=x(0<x<4),由勾股定理,得 AB=5,∵由(1)知,△PBQ∽△ABC,
∴==,即 ==,
∴PQ=x,QB=x,
S△APQ=PQ×AQ= x2+x= (x )2+,
∴当x=时,△APQ的面积最大,最大值是;
(3)存在。∵Rt△AQP≌Rt△ACP,∴AQ=AC
又∵Rt△AQP≌Rt△BQP,∴AQ=QB,∴AQ=QB=AC
在Rt△ABC中,由勾股定理得 BC2=AB2-AC2
∴BC=AC
∴λ=时,Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等。
9.5小时.
10.(1) (2)17米.
11.答案:延长CB至L,使BL=DN,
则Rt△ABL≌Rt△ADN,故AL=AN,
∵CM+CN+MN=2,CN+DN+CM+BM=1+1=2,
∴MN=DN+BM=BL+BM=ML,∴△AMN≌△AML(SSS),
设CM=x,CN=y,MN=z,x2+y2=z2,
∵x+y+z=2,则x=2-y-z,
∴(2-y-z)2+y2=z2,
整理得2y2+(2z-4)y+(4-4z)=0,
即:y2+(z-2)y+(2-2z)=0
∴△=(z-2)2-4(2-2z)≥0,
∴z2+4z-4≥0
又∵z>0,∴z>2-2
又∵z>0,∴z>2-2
∵S△AMN=S△AML=ML AB=z。
∴当z=2-2时,S△AMN取得最小值,为-1,故答案为:-1。
12.答案:解:(1)设矩形的边长PN=2y(mm),则PQ=y(mm),由条件可得△APN∽△ABC,
∴=,即=,解得y=,
∴PN=×2=(mm)。
答:这个矩形零件的两条边长分别为mm,mm。
(2)设PN=x(mm),由条件可得△APN∽△ABC,
∴=,即=,
解得PQ=80-x,
∴S=PN PQ=x(80-x)=-x2+80x=-(x-60)2+2400,
∴S的最大值为2400mm2,此时PN=60mm,PQ=80-×60=40(mm)
1.(舟山)当时,二次函数有最大值4,则实数的值为( )
A. B. 或 C. 2或 D. 2或或
2. 已知0≤x≤,那么函数y=-2x2+8x-6的最大值是( )
A. -10.5 B. 2 C. -2.5 D. -6
3. 若二次函数y=x2-2x+c的图象与y轴的交点为(0,-3),则此二次函数有( )
A. 最小值-2 B. 最小值-3 C. 最小值-4 D. 最大值-4
4. 下列四个说法中正确的是( )
①已知反比例函数y=,则当y≤时自变量x的取值范围是x≥4;
②点(x1,y1)和点(x2,y2)在反比例函数y=-的图象上,若x1<x2,则y1<y2;
③二次函数y=2x2+8x+13(-3≤x≤0)的最大值为13,最小值为7;
④已知函数y=x2+mx+1的图象,当x≤时,y随着x的增大而减小,则m=-。
A. ④ B. ①② C. ③④ D. 四个说法都不对
5. 如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与射线AC相交于点D。当△ODA是等边三角形时,这两个二次函数的最大值之和等于( )
A. B. C. 2 D.
6. 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 。
7. 如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF。则AF的最小值是 。
8. 在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP。
(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值;
(3)在Rt△ABC中,两条直角边BC、AC满足关系式BC=λAC,是否存在一个λ的值,使Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等。
9.如图,有一座抛物线型拱桥,已知桥下在正常水位AB时,水面宽8m,水位上升3m, 就达到警戒水位CD,这时水面宽4m,若洪水到来时,水位以每小时0.2m的速度上升,求水过警戒水位后几小时淹到桥拱顶.
10.如图,足球场上守门员在O处开出一高球,球从离地面1m的A处飞出(A在y轴上),运动员乙在距O点6m的B处发现球在自己头的正上方达到最高点M,距地面约4m高.球第一次落地后又弹起.据试验,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的表达式;
(2)运动员乙要抢到第二个落点D,他应再向前跑多少米 (取,)
11.(鄂州)如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为 。
12.(绍兴)课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm。要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。问加工成的正方形零件的边长是多少毫米?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题。
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1所示,此时,这个矩形零件的两条边长又分别为多少毫米?请你计算。
(2)如果原题中所要加工的零件只是一个矩形,如图2所示,这样,此矩形零件的两条边长就不能确定,但这个矩形的面积有最大值,求达到这个最大值时矩形零件的两条边长。
参考答案
1.解:二次函数的对称轴为直线,
①当,时,二次函数有最大值,
此时,,
解得,与矛盾,故值不存在;
②当,时,二次函数有最大值,
此时,,
解得(舍去),符合题意;
③当,时,二次函数有最大值,
此时,,
解得,
综上所述,的值为2或。故选C。
2. C 解析:∵y=-2x2+8x-6=-2(x-2)2+2,
∴该抛物线的对称轴是x=2,且在x<2上y随x的增大而增大。
又∵0≤x≤,∴当x=时,y取最大值,y最大=-2(-2)2+2=-2.5。
故选C。
3. C 解析:∵二次函数y=x2-2x+c的图象与y轴的交点为(0,-3),
∴c=-3,∴二次函数解析式为y=x2-2x-3,
∵y=x2-2x-3=(x-1)2-4,∴此二次函数当x=1时,有最小值-4。
故选C。
4. D 解析:①因为反比例函数y=,k=6的函数图象在一、三象限,
在第一象限内x≥4时,y≤;
在第三象限内所有的函数值都小于,即x<0。所以不正确。
②因为k=-<0,所以函数图象位于二、四象限内,
当x1、x2位于不同的象限内时,则不成立。
③因为a=2>0,所以函数图象开口向上,
当x= = = 2时,函数有最小值==5,所以不正确。
④因为a=>0,所以函数图象开口向上,
当x≤-时,y随x的增大而减小,
即x≤ m,所以 m≥,即m≤ ,不正确。
故选D。
5. C 解析:如图,连接PB、PC,由二次函数的性质,OB=PB,PC=AC,
∵△ODA是等边三角形,
∴∠AOD=∠OAD=60°,∴△POB和△ACP是等边三角形,
∵A(4,0),∴OA=4,∴点B、C的纵坐标之和为4×=2,
即两个二次函数的最大值之和等于2。故选C。
6. 6 解析:∵y=-x2+x+2,∴当y=0时,-x2+x+2=0,即-(x-2)(x+1)=0,解得 x=2或x=-1
因为P为第一象限点,
故设P(x,y)(0<x<2,y>0),
∴C=2(x+y)=2(x-x2+x+2)=-2(x-1)2+6,
∴当x=1时,C最大值=6,
即四边形OAPB周长的最大值为6,
7. 5 解析:设BE=x,则EC=4-x,
∵AE⊥EF,∴∠AEF=90°,∴∠AEB+∠FEC=90°,
而∠AEB+∠BAE=90°,∴∠BAE=∠FEC,∴Rt△ABE∽Rt△ECF,
∴=,即=,解得FC=,
∴DF=4-FC=4-=x2-x+4=(x-2)2+3
当x=2时,DF有最小值3,
∵AF2=AD2+DF2,∴AF的最小值为5。
8. 解:(1)不论点P在BC边上何处时,都有∠PQB=∠C=90°,∠B=∠B,
∴△PBQ∽△ABC;
(2)设BP=x(0<x<4),由勾股定理,得 AB=5,∵由(1)知,△PBQ∽△ABC,
∴==,即 ==,
∴PQ=x,QB=x,
S△APQ=PQ×AQ= x2+x= (x )2+,
∴当x=时,△APQ的面积最大,最大值是;
(3)存在。∵Rt△AQP≌Rt△ACP,∴AQ=AC
又∵Rt△AQP≌Rt△BQP,∴AQ=QB,∴AQ=QB=AC
在Rt△ABC中,由勾股定理得 BC2=AB2-AC2
∴BC=AC
∴λ=时,Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等。
9.5小时.
10.(1) (2)17米.
11.答案:延长CB至L,使BL=DN,
则Rt△ABL≌Rt△ADN,故AL=AN,
∵CM+CN+MN=2,CN+DN+CM+BM=1+1=2,
∴MN=DN+BM=BL+BM=ML,∴△AMN≌△AML(SSS),
设CM=x,CN=y,MN=z,x2+y2=z2,
∵x+y+z=2,则x=2-y-z,
∴(2-y-z)2+y2=z2,
整理得2y2+(2z-4)y+(4-4z)=0,
即:y2+(z-2)y+(2-2z)=0
∴△=(z-2)2-4(2-2z)≥0,
∴z2+4z-4≥0
又∵z>0,∴z>2-2
又∵z>0,∴z>2-2
∵S△AMN=S△AML=ML AB=z。
∴当z=2-2时,S△AMN取得最小值,为-1,故答案为:-1。
12.答案:解:(1)设矩形的边长PN=2y(mm),则PQ=y(mm),由条件可得△APN∽△ABC,
∴=,即=,解得y=,
∴PN=×2=(mm)。
答:这个矩形零件的两条边长分别为mm,mm。
(2)设PN=x(mm),由条件可得△APN∽△ABC,
∴=,即=,
解得PQ=80-x,
∴S=PN PQ=x(80-x)=-x2+80x=-(x-60)2+2400,
∴S的最大值为2400mm2,此时PN=60mm,PQ=80-×60=40(mm)
