2021- 2022学年人教版七年级数学下册5.2平行线的判定专项测试卷 (word版含解析)
文档属性
| 名称 | 2021- 2022学年人教版七年级数学下册5.2平行线的判定专项测试卷 (word版含解析) | 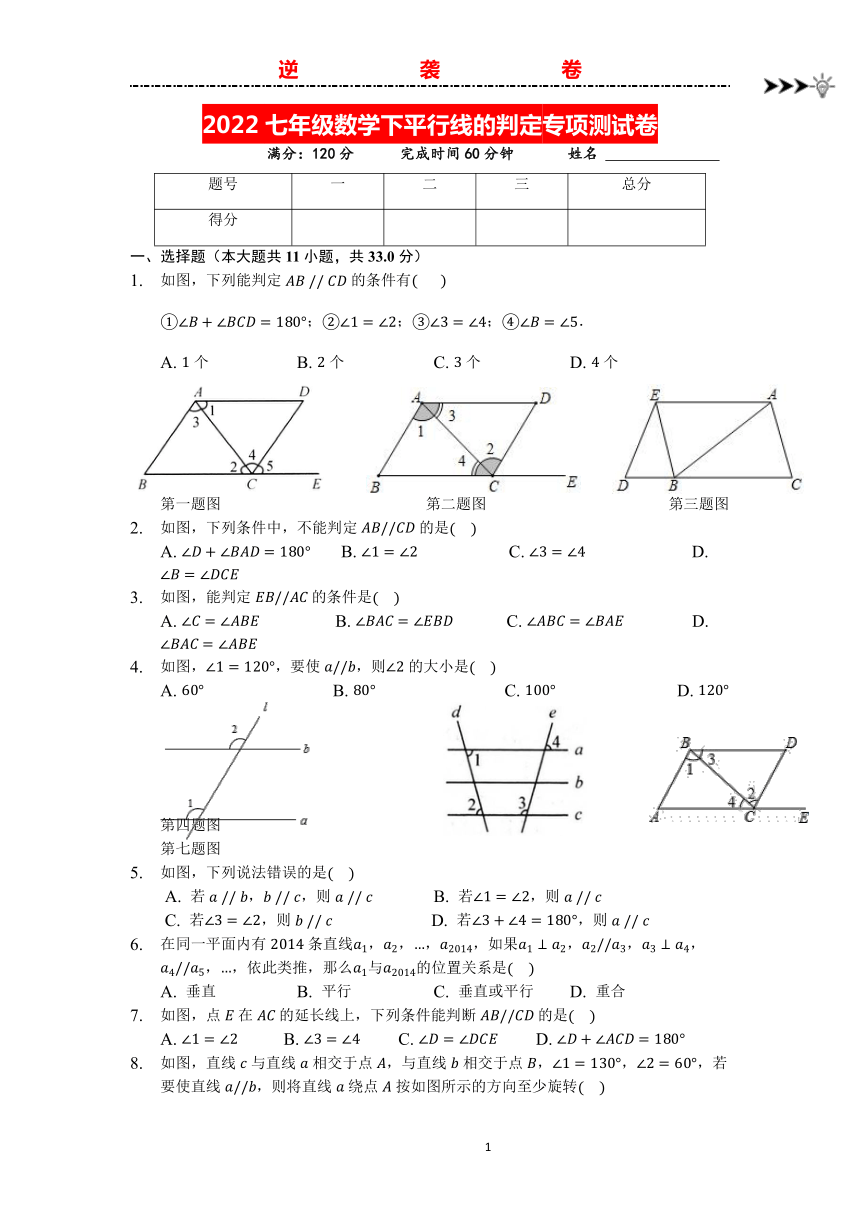 | |
| 格式 | docx | ||
| 文件大小 | 235.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 10:33:21 | ||
图片预览




文档简介
2022七年级数学下平行线的判定专项测试卷
满分:120分 完成时间60分钟 姓名
题号 一 二 三 总分
得分
一、选择题(本大题共11小题,共33.0分)
如图,下列能判定的条件有
;;;.
A. 个 B. 个 C. 个 D. 个
第一题图 第二题图 第三题图
如图,下列条件中,不能判定的是
A. B. C. D.
如图,能判定的条件是
A. B. C. D.
如图,,要使,则的大小是
A. B. C. D.
第四题图 第五题图 第七题图
如图,下列说法错误的是
若,,则 B. 若,则
C. 若,则 D. 若,则
在同一平面内有条直线,,,,如果,,,,,依此类推,那么与的位置关系是
A. 垂直 B. 平行 C. 垂直或平行 D. 重合
如图,点在的延长线上,下列条件能判断的是
A. B. C. D.
如图,直线与直线相交于点,与直线相交于点,,,若要使直线,则将直线绕点按如图所示的方向至少旋转
A. B. C. D.
第八题图 第九题图 第十题图
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 两直线平行,同位角相等
下列条件中,能说明的条件有个
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
下列说法:两点之间的距离是两点间的线段的长度;过一点有且只有一条直线与已知直线平行;两点之间的所有连线中,线段最短;若,,则与的关系是平行;只有一个公共点的两条直线叫做相交直线;⑥过一点有且只有一条直线与已知直线垂直;⑦垂线段最短
其中正确的是____.
如图,下列条件中:
;;;;
则一定能判定的条件有______填写所有正确的序号.
第十二题图 第十三题图
以下三种沿所在直线折叠纸带的方法:如图,展开后测得;如图,展开后测得且;如图,测得其中能判定纸带两条边线,互相平行的是________填序号.
一副直角三角尺叠放如图所示,现将的三角尺固定不动,将含的三角尺绕顶点顺时针转动旋转角不超过度,使两块三角尺至少有一组边互相平行.如图:当时,则
如图,,,,则 时,.
三、解答题(本大题共8小题,共75.0分)
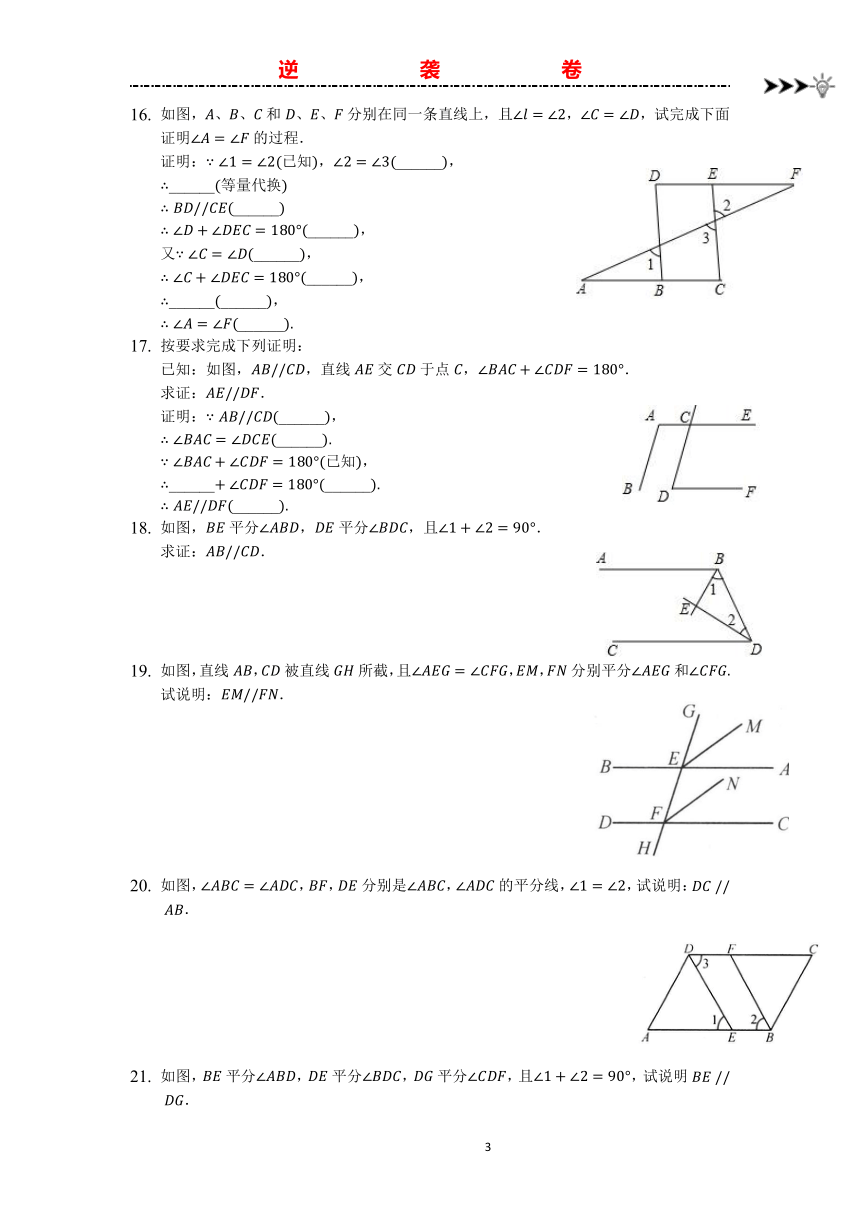
如图,、、和、、分别在同一条直线上,且,,试完成下面证明的过程.
证明:已知,______,
______等量代换
______
______,
又______,
______,
____________,
______
按要求完成下列证明:
已知:如图,,直线交于点,.
求证:.
证明:______,
______
已知,
____________
______
如图,平分,平分,且.
求证:.
如图,直线,被直线所截,且,,分别平分和试说明:.
如图,,,分别是,的平分线,,试说明:.
如图,平分,平分,平分,且,试说明.
在中,是边上一点,且,是经过点的一条直线.
若直线,垂足为点
依题意补全图.
若,,则______,______
如图,若直线交边于点,且,求证:.
如图,,平分,平分,F.问:与的位置关系怎样试说明理由.
答案和解析
1.【答案】
【解答】
解:,同旁内角互补,两直线平行,则能判定,故此选项正确;
,但,不是截、所得的内错角,所不能判定,故此选项错误;
,内错角相等,两直线平行,则能判定,故此选项正确;
,同位角相等,两直线平行,则能判定,故此选项正确.
满足条件的有,,.
故选C.
2.【答案】
【解答】
解:根据,可得;
根据,可得;
根据,可得,不能判定;
根据,可得;
故选C.
3.【答案】
【解答】
解:、不能判断出,故本选项错误;
B、不能判断出,故本选项错误;
C、只能判断出,不能判断出,故本选项错误;
D、,根据内错角相等,两直线平行,可以得出,故本选项正确.
故选D.
4.【答案】
【解答】
解:由图可以得出,是同位角,
当时,
可得.
所以要使,则的大小是.
故选:.
5.【答案】
【解答】
解:若,,则,利用了平行的传递性,故此项不符合题意;
B.若,则,利用了内错角相等,两直线平行,故此项不符合题意;
C.若,则,不能判断,故此项符合题意;
D.若,则,先利用对顶角相等,再利用同旁内角互补,两直线平行,故此项不符合题意.
故选C.
6.【答案】
【解析】解:,,,,,
,,,
以四次为一个循环,,,,
规律:下标除以余数为或垂直,下标除以余数为或平行,
的余数为,
,
所以直线与的位置关系是:.
故选A.
7.【答案】
【解析】解:根据内错角相等,两直线平行即可证得;
B.根据内错角相等,两直线平行即可证得,不能证;
C.根据内错角相等,两直线平行即可证得,不能证;
D.根据同旁内角互补,两直线平行,即可证得,不能证.
故选:.
8.【答案】
【解答】解:
,
若要使直线,则应该为,
又,
,
直线绕点按顺时针方向至少旋转:,
故选:.
9.【答案】
【解答】
解:、和的是对顶角,不能判断,此选项不正确;
B、和的对顶角是内错角,又相等,所以,此选项正确;
C、和的是内错角,又相等,故AD,不是,此选项错误;
D、和互为同旁内角,同旁内角相等两直线不平行,此选项错误.
故选B.
10.【答案】
【解答】
解:,可得,错误;
,可得,正确;
,不能判断,错误;
,不能判断,错误;
,可得,正确;
,可得,错误;
综上诉述共个正确.
故选B.
11.【答案】
【解答】
解:两点之间的距离是两点间的线段的长度,正确;
过直线外一点有且只有一条直线与已知直线平行,错误;
两点之间的所有连线中,线段最短,正确;
在同一平面内,垂直于同一直线的两条直线平行,错误;
只有一个公共点的两条直线叫做相交直线,正确;
故答案为.
12.【答案】
【解答】
解:,
;
,
;
,
;
,
,
故答案为:.
13.【答案】
【解答】
解:,根据内错角相等,两直线平行进行判定,故正确;
且,由图可知,,
,
内错角相等,两直线平行,
故正确;
测得,
与即不是内错角也不是同位角,
不一定能判定两直线平行,故错误;
故答案为.
14.【答案】,,,
【解答】
解:如下图:
当时,,则,所以;
当时,;
当时,,所以;
当时,,所以.
故答案为,,,.
15.【答案】
16.【解析】证明:已知,对顶角相等,等量代换,
同位角相等,两直线平行,
两直线平行,同旁内角互补,
又已知,
等量代换,
同旁内角互补,两直线平行,
两直线平行,内错角相等.
17.【解析】证明:已知,
两直线平行,同位角相等.
已知,
等量代换.
同旁内角互补,两直线平行.
18.【答案】解:平分,平分已知,
,角平分线定义,
,
,
同旁内角互补,两直线平行.
19.【答案】解:因为,分别平分和,
所以,.
因为,
所以.
所以.
20.【答案】,分别是,的角平分线,
,,
,
,
,
,
.
21.【答案】解:平分,平分,
,,
,
,
,
,
.
22.【解析】解:如图所示:
,,
,
,
,
,
,
故答案为:,;
,
,,
,
,
,
.
23.【答案】解:.
理由如下:
因为平分,平分, 所以,.
因为,所以, 所以.
因为,所以, 所以.
逆 袭 卷
满分:120分 完成时间60分钟 姓名
题号 一 二 三 总分
得分
一、选择题(本大题共11小题,共33.0分)
如图,下列能判定的条件有
;;;.
A. 个 B. 个 C. 个 D. 个
第一题图 第二题图 第三题图
如图,下列条件中,不能判定的是
A. B. C. D.
如图,能判定的条件是
A. B. C. D.
如图,,要使,则的大小是
A. B. C. D.
第四题图 第五题图 第七题图
如图,下列说法错误的是
若,,则 B. 若,则
C. 若,则 D. 若,则
在同一平面内有条直线,,,,如果,,,,,依此类推,那么与的位置关系是
A. 垂直 B. 平行 C. 垂直或平行 D. 重合
如图,点在的延长线上,下列条件能判断的是
A. B. C. D.
如图,直线与直线相交于点,与直线相交于点,,,若要使直线,则将直线绕点按如图所示的方向至少旋转
A. B. C. D.
第八题图 第九题图 第十题图
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线平行 D. 两直线平行,同位角相等
下列条件中,能说明的条件有个
A. B. C. D.
二、填空题(本大题共5小题,共15.0分)
下列说法:两点之间的距离是两点间的线段的长度;过一点有且只有一条直线与已知直线平行;两点之间的所有连线中,线段最短;若,,则与的关系是平行;只有一个公共点的两条直线叫做相交直线;⑥过一点有且只有一条直线与已知直线垂直;⑦垂线段最短
其中正确的是____.
如图,下列条件中:
;;;;
则一定能判定的条件有______填写所有正确的序号.
第十二题图 第十三题图
以下三种沿所在直线折叠纸带的方法:如图,展开后测得;如图,展开后测得且;如图,测得其中能判定纸带两条边线,互相平行的是________填序号.
一副直角三角尺叠放如图所示,现将的三角尺固定不动,将含的三角尺绕顶点顺时针转动旋转角不超过度,使两块三角尺至少有一组边互相平行.如图:当时,则
如图,,,,则 时,.
三、解答题(本大题共8小题,共75.0分)
如图,、、和、、分别在同一条直线上,且,,试完成下面证明的过程.
证明:已知,______,
______等量代换
______
______,
又______,
______,
____________,
______
按要求完成下列证明:
已知:如图,,直线交于点,.
求证:.
证明:______,
______
已知,
____________
______
如图,平分,平分,且.
求证:.
如图,直线,被直线所截,且,,分别平分和试说明:.
如图,,,分别是,的平分线,,试说明:.
如图,平分,平分,平分,且,试说明.
在中,是边上一点,且,是经过点的一条直线.
若直线,垂足为点
依题意补全图.
若,,则______,______
如图,若直线交边于点,且,求证:.
如图,,平分,平分,F.问:与的位置关系怎样试说明理由.
答案和解析
1.【答案】
【解答】
解:,同旁内角互补,两直线平行,则能判定,故此选项正确;
,但,不是截、所得的内错角,所不能判定,故此选项错误;
,内错角相等,两直线平行,则能判定,故此选项正确;
,同位角相等,两直线平行,则能判定,故此选项正确.
满足条件的有,,.
故选C.
2.【答案】
【解答】
解:根据,可得;
根据,可得;
根据,可得,不能判定;
根据,可得;
故选C.
3.【答案】
【解答】
解:、不能判断出,故本选项错误;
B、不能判断出,故本选项错误;
C、只能判断出,不能判断出,故本选项错误;
D、,根据内错角相等,两直线平行,可以得出,故本选项正确.
故选D.
4.【答案】
【解答】
解:由图可以得出,是同位角,
当时,
可得.
所以要使,则的大小是.
故选:.
5.【答案】
【解答】
解:若,,则,利用了平行的传递性,故此项不符合题意;
B.若,则,利用了内错角相等,两直线平行,故此项不符合题意;
C.若,则,不能判断,故此项符合题意;
D.若,则,先利用对顶角相等,再利用同旁内角互补,两直线平行,故此项不符合题意.
故选C.
6.【答案】
【解析】解:,,,,,
,,,
以四次为一个循环,,,,
规律:下标除以余数为或垂直,下标除以余数为或平行,
的余数为,
,
所以直线与的位置关系是:.
故选A.
7.【答案】
【解析】解:根据内错角相等,两直线平行即可证得;
B.根据内错角相等,两直线平行即可证得,不能证;
C.根据内错角相等,两直线平行即可证得,不能证;
D.根据同旁内角互补,两直线平行,即可证得,不能证.
故选:.
8.【答案】
【解答】解:
,
若要使直线,则应该为,
又,
,
直线绕点按顺时针方向至少旋转:,
故选:.
9.【答案】
【解答】
解:、和的是对顶角,不能判断,此选项不正确;
B、和的对顶角是内错角,又相等,所以,此选项正确;
C、和的是内错角,又相等,故AD,不是,此选项错误;
D、和互为同旁内角,同旁内角相等两直线不平行,此选项错误.
故选B.
10.【答案】
【解答】
解:,可得,错误;
,可得,正确;
,不能判断,错误;
,不能判断,错误;
,可得,正确;
,可得,错误;
综上诉述共个正确.
故选B.
11.【答案】
【解答】
解:两点之间的距离是两点间的线段的长度,正确;
过直线外一点有且只有一条直线与已知直线平行,错误;
两点之间的所有连线中,线段最短,正确;
在同一平面内,垂直于同一直线的两条直线平行,错误;
只有一个公共点的两条直线叫做相交直线,正确;
故答案为.
12.【答案】
【解答】
解:,
;
,
;
,
;
,
,
故答案为:.
13.【答案】
【解答】
解:,根据内错角相等,两直线平行进行判定,故正确;
且,由图可知,,
,
内错角相等,两直线平行,
故正确;
测得,
与即不是内错角也不是同位角,
不一定能判定两直线平行,故错误;
故答案为.
14.【答案】,,,
【解答】
解:如下图:
当时,,则,所以;
当时,;
当时,,所以;
当时,,所以.
故答案为,,,.
15.【答案】
16.【解析】证明:已知,对顶角相等,等量代换,
同位角相等,两直线平行,
两直线平行,同旁内角互补,
又已知,
等量代换,
同旁内角互补,两直线平行,
两直线平行,内错角相等.
17.【解析】证明:已知,
两直线平行,同位角相等.
已知,
等量代换.
同旁内角互补,两直线平行.
18.【答案】解:平分,平分已知,
,角平分线定义,
,
,
同旁内角互补,两直线平行.
19.【答案】解:因为,分别平分和,
所以,.
因为,
所以.
所以.
20.【答案】,分别是,的角平分线,
,,
,
,
,
,
.
21.【答案】解:平分,平分,
,,
,
,
,
,
.
22.【解析】解:如图所示:
,,
,
,
,
,
,
故答案为:,;
,
,,
,
,
,
.
23.【答案】解:.
理由如下:
因为平分,平分, 所以,.
因为,所以, 所以.
因为,所以, 所以.
逆 袭 卷
