2021-2022学年人教版七年级数学下册 5.1相交线 寒假预习同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册 5.1相交线 寒假预习同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 11:14:43 | ||
图片预览




文档简介
2021-2022学年人教版七年级数学下册《5-1相交线》寒假预习同步练习(附答案)
1.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )
A. B.
C. D.
2.如图,直线AB,CD相交于点O,∠2﹣∠1=15°,∠3=130°.则∠2的度数是( )
A.37.5° B.75° C.50° D.65°
3.下列各图中,∠1和∠2是对顶角的是( )
A.B. C.D.
4.下列各图中,过直线l外点P画l的垂线CD,三角板操作正确的是( )
A.B. C.D.
5.如图,能表示点P到直线m的距离的是( )的长度.
A.线段PA B.线段PB C.线段PC D.线段AC
6.如图,若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.在同一平面内,经过一点有并且只有一条直线与已知直线垂直
7.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
8.平面内有八条直线,两两相交最多有m个交点,最少有n个交点,则m+n= .
9.如图,AB、CD相交于点O,OB平分∠DOE,若∠AOC=30°,则∠DOE的度数是 .
10.如果4条直线两两相交,最多有 个交点,最少有 个交点.
11.如图,直线AB,CD相交于点O,OA平分∠EOC.若∠AOE=36°,则∠DOE= °.
12.已知∠1和∠2是对顶角,若∠1=28°,则∠2的余角等于 °.
13.点O为线段AB上一点,不与点A、B重合,OC⊥OD于点O,若∠AOC=35°,则∠BOD的度数为 .
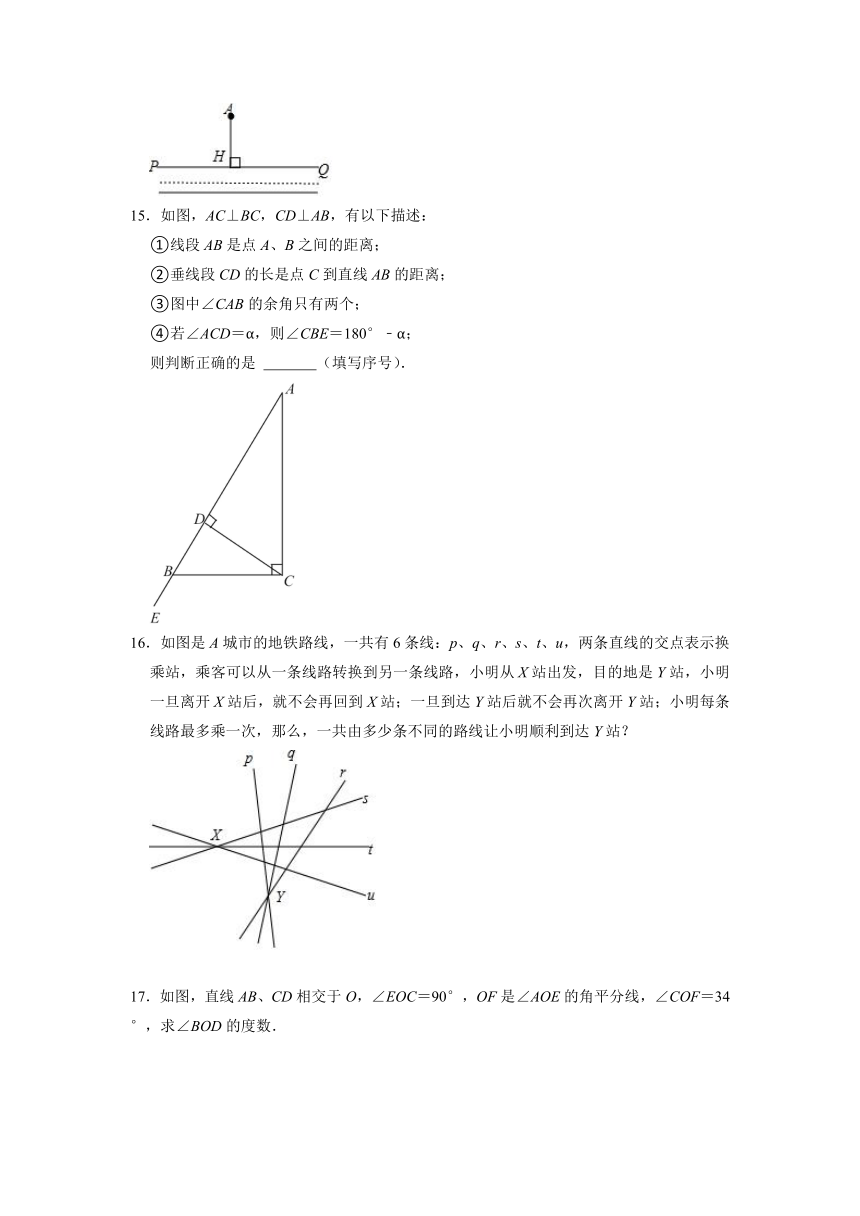
14.如图,现要从村庄A修建一条连接公路PQ的最短路径,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是 .
15.如图,AC⊥BC,CD⊥AB,有以下描述:
①线段AB是点A、B之间的距离;
②垂线段CD的长是点C到直线AB的距离;
③图中∠CAB的余角只有两个;
④若∠ACD=α,则∠CBE=180°﹣α;
则判断正确的是 (填写序号).
16.如图是A城市的地铁路线,一共有6条线:p、q、r、s、t、u,两条直线的交点表示换乘站,乘客可以从一条线路转换到另一条线路,小明从X站出发,目的地是Y站,小明一旦离开X站后,就不会再回到X站;一旦到达Y站后就不会再次离开Y站;小明每条线路最多乘一次,那么,一共由多少条不同的路线让小明顺利到达Y站?
17.如图,直线AB、CD相交于O,∠EOC=90°,OF是∠AOE的角平分线,∠COF=34°,求∠BOD的度数.
18.如图,直线AB、CD相交于点O,过点O作OE⊥AB,射线OF平分∠AOC,∠AOF=25°.
求:(1)∠BOD的度数;
(2)∠COE的度数.
19.平面内三条直线两两相交,求交点的个数,并画图说明.
20.(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图中对顶角和邻补角的个数
(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图中对顶角和邻补角的个数
(3)依此类推,n条直线相交,最少有多少个交点,最多有多少个交点,对顶角有多少对,邻补角有多少对.
21.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
22.如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
23.平面内两条直线AB、CD相交于点O,∠EOF=90°,OB平分∠COF.
(1)如图1:
①若∠AOE=20°,则∠DOF= °;
②请写出∠DOF和∠AOE的数量关系,并说明理由.
(2)如图2,∠DOF与∠AOE的数量关系是 .
24.已知,点O在直线AB上,在直线AB外取一点C,画射线OC,OD平分∠BOC.射线OE在直线AB上方,且OE⊥OD于O.
(1)如图1,如果点C在直线AB上方,且∠BOC=30°,
①依题意补全图1;
②求∠AOE的度数(0°<∠AOE<180°);
(2)如果点C在直线AB外,且∠BOC=α,请直接写出∠AOE的度数.(用含α的代数式表示,且0°<∠AOE<180°)
25.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
参考答案
1.解:A.直线l2不经过点M,故本选项不合题意;
B.点M在直线l1上,故本选项不合题意;
C.点M在直线l1上,故本选项不合题意;
D.直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M,故本选项符合题意;
故选:D.
2.解:∵∠3=130°,
∴∠1=180°﹣130°=50°,
∵∠2﹣∠1=15°,
∴∠2=50°+15°=65°,
故选:D.
3.解:根据对顶角的定义可得,D是对顶角,
故选:D.
4.解:根据分析可得D的画法正确,
故选:D.
5.解:∵PB⊥m,
∴能表示点P到直线m的距离的是线段PB的长度.
故选:B.
6.解:若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是垂线段最短,
故选:B.
7.解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5不是内错角,故C错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
8.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:8×(8﹣1)÷2=28,
即m=28;
则m+n=28+1=29.
故答案为:29.
9.解:∵∠AOC和∠BOD是对顶角,
∴∠BOD=∠AOC=30°,
∵OB平分∠DOE,
∴∠DOE=2∠BOD=60°.
故答案为:60°.
10.解:n条直线相交,最多有n(n﹣1)个交点.
当n=4时,,
即如果4条直线两两相交,最多有6个交点,最少有1个交点.
故答案为:6、1.
11.解:∠DOE=∠COD﹣∠COE
=180°﹣36°×2
=180°﹣72°
=108°.
故答案为:108.
12.解:∵∠1和∠2是对顶角,
∴∠2=∠1=28°.
∴∠2的余角=90°﹣28°=62°.
故答案为:62.
13.解:当OC和OD在AB同一侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=35°,
∴∠BOD=90°﹣∠AOC=90°﹣35°=55°,
当OC和OD在AB同异侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOC=35°,
∴∠AOD=55°,
∴∠BOD=180°﹣∠AOD=180°﹣55°=125°.
∴∠BOD的度数为55°或125°.
故答案为:55°或125°.
14.解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故答案为:垂线段最短.
15.解:①线段AB的长度是点A、B之间的距离,故①错误;
②∵CD⊥AB,
∴垂线段CD的长是点C到直线AB的距离,
故②正确;
③∵AC⊥BC,CD⊥AB,
∴∠ACB=∠ADC=90°,
∴∠CAB+∠ABC=90°,∠CAB+∠ACD=90°,
∴图中∠CAB的余角只有两个,
故③正确;
④∵∠ACD+∠BCD=90°,∠BCD+∠DBC=90°,
∴∠ACD=∠DBC=α,
∴∠CBE=180°﹣α,
故④正确;
故答案为:②③④.
16.解:根据图形可知:一共由9条不同的路线让小明顺利到达Y站.
17.解:∵∠EOC=90°,∠COF=34°,
∴∠EOF=90°﹣34°=56°,
又∵OF平分∠AOE,
∴∠AOF=∠EOF=56°,
∵∠COF=34°,
∴∠AOC=56°﹣34°=22°,
则∠BOD=∠AOC=22°.
18.解:(1)∵射线OF平分∠AOC,∠AOF=25°,
∴∠AOC=2∠AOF=50°,
∴∠BOD=∠AOC=50°;
(2)∵OE⊥AB,
∴∠AOE=90°,
∵∠AOC=50°,
∴∠COE=90°﹣∠AOC=90°﹣50°=40°.
19.解:如图,在同一平面内,两两相交的三条直线的只有这两种情况,
所以交点有1或3个.
20.解:(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
对顶角:6对,邻补角:12对;
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
对顶角:12对,邻补角:24对;
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有n(n﹣1)对,邻补角有2n(n﹣1)对.
故答案为:(1)1,3;(2)1,6;(3)1,,n(n﹣1),2n(n﹣1).
21.解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
22.解:(1)OF⊥OD.
证明:∵OD平分∠BOE,OF平分∠AOE,
∴∠FOE=∠AOE,∠EOD=∠EOB.
∵∠AOE+∠EOB=180°,
∴∠FOD=∠FOE+∠EOD=(∠AOE+∠EOB)=90°.
∴OF⊥OD.
(2)∵∠AOC:∠AOD=1:5,∠AOC=∠BOD,
∴∠BOD:∠AOD=1:5.
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°.
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF=∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,
∴∠EOF=60°.
23.解:(1)①∵∠EOF=90°,∠AOE=20°,
∴∠BOF=180°﹣∠EOF﹣∠AOE=70°,
∵OB平分∠COF,
∴∠COF=2∠BOF=140°,
∴∠DOF=180°﹣∠COF=40°,
故答案为:40°,
②∠DOF=2∠AOE,
理由是:设∠AOE=x,
∵∠EOF=90°,
∴∠BOF=180°﹣∠EOF﹣∠AOE=90°﹣x,
∵OB平分∠COF,
∴∠COF=2∠BOF=180°﹣2x,
∴∠DOF=180°﹣∠COF=2x,
∴∠DOF=2∠AOE;
(2)∠DOF=2∠AOE,
理由是:设∠AOE=y,
∵∠EOF=90°,
∴∠BOF=180°﹣∠EOF﹣∠AOE=90°﹣y,
∵OB平分∠COF,
∴∠COF=2∠BOF=180°﹣2y,
∴∠DOF=180°﹣∠COF=2y,
∴∠DOF=2∠AOE.
24.解:(1)①如图所示:
②∵∠BOC=30°,OD平分∠BOC,
∴∠BOD=∠BOC=15°,
∵OD⊥OE,
∴∠DOE=90°,
又∵点O在直线AB上,
∴∠AOE=180°﹣90°﹣15°=75°;
(2)分两种情况:
①当点C在直线AB上方时,如图1,
同理可得,∠BOD=,∠DOE=90°,
∴∠AOE=180°﹣90°﹣=90°﹣;
②当点C在直线AB下方时,如图2,
∵OD平分∠BOC,
∴∠BOD=α,
∵OD⊥OE,
∴∠DOE=90°,
∴∠BOE=90°﹣α,
又∵点O在直线AB上,
∴∠AOE=180°﹣(90°﹣α)=90°+α.
综上所述,∠AOE的度数为90°﹣或90°+α.
25.解:因为两个交点可以形成2对同旁内角,而三个交点形成的同旁内角的对数为6对,
(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4﹣1)×(4﹣2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
1.根据语句“直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M.”画出的图形是( )
A. B.
C. D.
2.如图,直线AB,CD相交于点O,∠2﹣∠1=15°,∠3=130°.则∠2的度数是( )
A.37.5° B.75° C.50° D.65°
3.下列各图中,∠1和∠2是对顶角的是( )
A.B. C.D.
4.下列各图中,过直线l外点P画l的垂线CD,三角板操作正确的是( )
A.B. C.D.
5.如图,能表示点P到直线m的距离的是( )的长度.
A.线段PA B.线段PB C.线段PC D.线段AC
6.如图,若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.在同一平面内,经过一点有并且只有一条直线与已知直线垂直
7.如图,下列结论中错误的是( )
A.∠1与∠2是同旁内角 B.∠1与∠6是内错角
C.∠2与∠5是内错角 D.∠3与∠5是同位角
8.平面内有八条直线,两两相交最多有m个交点,最少有n个交点,则m+n= .
9.如图,AB、CD相交于点O,OB平分∠DOE,若∠AOC=30°,则∠DOE的度数是 .
10.如果4条直线两两相交,最多有 个交点,最少有 个交点.
11.如图,直线AB,CD相交于点O,OA平分∠EOC.若∠AOE=36°,则∠DOE= °.
12.已知∠1和∠2是对顶角,若∠1=28°,则∠2的余角等于 °.
13.点O为线段AB上一点,不与点A、B重合,OC⊥OD于点O,若∠AOC=35°,则∠BOD的度数为 .
14.如图,现要从村庄A修建一条连接公路PQ的最短路径,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是 .
15.如图,AC⊥BC,CD⊥AB,有以下描述:
①线段AB是点A、B之间的距离;
②垂线段CD的长是点C到直线AB的距离;
③图中∠CAB的余角只有两个;
④若∠ACD=α,则∠CBE=180°﹣α;
则判断正确的是 (填写序号).
16.如图是A城市的地铁路线,一共有6条线:p、q、r、s、t、u,两条直线的交点表示换乘站,乘客可以从一条线路转换到另一条线路,小明从X站出发,目的地是Y站,小明一旦离开X站后,就不会再回到X站;一旦到达Y站后就不会再次离开Y站;小明每条线路最多乘一次,那么,一共由多少条不同的路线让小明顺利到达Y站?
17.如图,直线AB、CD相交于O,∠EOC=90°,OF是∠AOE的角平分线,∠COF=34°,求∠BOD的度数.
18.如图,直线AB、CD相交于点O,过点O作OE⊥AB,射线OF平分∠AOC,∠AOF=25°.
求:(1)∠BOD的度数;
(2)∠COE的度数.
19.平面内三条直线两两相交,求交点的个数,并画图说明.
20.(1)三条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图中对顶角和邻补角的个数
(2)四条直线相交,最少有 个交点,最多有 个交点,分别画出图形,并数出图中对顶角和邻补角的个数
(3)依此类推,n条直线相交,最少有多少个交点,最多有多少个交点,对顶角有多少对,邻补角有多少对.
21.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
22.如图,直线AB,CD相交于点O,OD平分∠BOE,OF平分∠AOE
(1)判断OF与OD的位置关系,并进行证明.
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
23.平面内两条直线AB、CD相交于点O,∠EOF=90°,OB平分∠COF.
(1)如图1:
①若∠AOE=20°,则∠DOF= °;
②请写出∠DOF和∠AOE的数量关系,并说明理由.
(2)如图2,∠DOF与∠AOE的数量关系是 .
24.已知,点O在直线AB上,在直线AB外取一点C,画射线OC,OD平分∠BOC.射线OE在直线AB上方,且OE⊥OD于O.
(1)如图1,如果点C在直线AB上方,且∠BOC=30°,
①依题意补全图1;
②求∠AOE的度数(0°<∠AOE<180°);
(2)如果点C在直线AB外,且∠BOC=α,请直接写出∠AOE的度数.(用含α的代数式表示,且0°<∠AOE<180°)
25.复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想.
(1)如图1,直线l1,l2被直线l3所截,在这个基本图形中,形成了 对同旁内角.
(2)如图2,平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有 对同旁内角.
(3)平面内四条直线两两相交,最多可以形成 对同旁内角.
(4)平面内n条直线两两相交,最多可以形成 对同旁内角.
参考答案
1.解:A.直线l2不经过点M,故本选项不合题意;
B.点M在直线l1上,故本选项不合题意;
C.点M在直线l1上,故本选项不合题意;
D.直线l1与直线l2相交,点M在直线l1上,直线l2不经过点M,故本选项符合题意;
故选:D.
2.解:∵∠3=130°,
∴∠1=180°﹣130°=50°,
∵∠2﹣∠1=15°,
∴∠2=50°+15°=65°,
故选:D.
3.解:根据对顶角的定义可得,D是对顶角,
故选:D.
4.解:根据分析可得D的画法正确,
故选:D.
5.解:∵PB⊥m,
∴能表示点P到直线m的距离的是线段PB的长度.
故选:B.
6.解:若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是垂线段最短,
故选:B.
7.解:A、∠1与∠2是同旁内角,正确,不合题意;
B、∠1与∠6是内错角,正确,不合题意;
C、∠2与∠5不是内错角,故C错误,符合题意;
D、∠3与∠5是同位角,正确,不合题意;
故选:C.
8.解:根据题意可得:8条直线相交于一点时交点最少,此时交点为1个,
即n=1;
任意两直线相交都产生一个交点时,交点最多,
∴此时交点为:8×(8﹣1)÷2=28,
即m=28;
则m+n=28+1=29.
故答案为:29.
9.解:∵∠AOC和∠BOD是对顶角,
∴∠BOD=∠AOC=30°,
∵OB平分∠DOE,
∴∠DOE=2∠BOD=60°.
故答案为:60°.
10.解:n条直线相交,最多有n(n﹣1)个交点.
当n=4时,,
即如果4条直线两两相交,最多有6个交点,最少有1个交点.
故答案为:6、1.
11.解:∠DOE=∠COD﹣∠COE
=180°﹣36°×2
=180°﹣72°
=108°.
故答案为:108.
12.解:∵∠1和∠2是对顶角,
∴∠2=∠1=28°.
∴∠2的余角=90°﹣28°=62°.
故答案为:62.
13.解:当OC和OD在AB同一侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=35°,
∴∠BOD=90°﹣∠AOC=90°﹣35°=55°,
当OC和OD在AB同异侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOC=35°,
∴∠AOD=55°,
∴∠BOD=180°﹣∠AOD=180°﹣55°=125°.
∴∠BOD的度数为55°或125°.
故答案为:55°或125°.
14.解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故答案为:垂线段最短.
15.解:①线段AB的长度是点A、B之间的距离,故①错误;
②∵CD⊥AB,
∴垂线段CD的长是点C到直线AB的距离,
故②正确;
③∵AC⊥BC,CD⊥AB,
∴∠ACB=∠ADC=90°,
∴∠CAB+∠ABC=90°,∠CAB+∠ACD=90°,
∴图中∠CAB的余角只有两个,
故③正确;
④∵∠ACD+∠BCD=90°,∠BCD+∠DBC=90°,
∴∠ACD=∠DBC=α,
∴∠CBE=180°﹣α,
故④正确;
故答案为:②③④.
16.解:根据图形可知:一共由9条不同的路线让小明顺利到达Y站.
17.解:∵∠EOC=90°,∠COF=34°,
∴∠EOF=90°﹣34°=56°,
又∵OF平分∠AOE,
∴∠AOF=∠EOF=56°,
∵∠COF=34°,
∴∠AOC=56°﹣34°=22°,
则∠BOD=∠AOC=22°.
18.解:(1)∵射线OF平分∠AOC,∠AOF=25°,
∴∠AOC=2∠AOF=50°,
∴∠BOD=∠AOC=50°;
(2)∵OE⊥AB,
∴∠AOE=90°,
∵∠AOC=50°,
∴∠COE=90°﹣∠AOC=90°﹣50°=40°.
19.解:如图,在同一平面内,两两相交的三条直线的只有这两种情况,
所以交点有1或3个.
20.解:(1)三条直线相交,最少有1个交点,最多有3个交点,如图:
对顶角:6对,邻补角:12对;
(2)四条直线相交,最少有1个交点,最多有6个交点,如图:
对顶角:12对,邻补角:24对;
(3)n条直线相交,最少有1个交点,最多有个交点,对顶角有n(n﹣1)对,邻补角有2n(n﹣1)对.
故答案为:(1)1,3;(2)1,6;(3)1,,n(n﹣1),2n(n﹣1).
21.解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
22.解:(1)OF⊥OD.
证明:∵OD平分∠BOE,OF平分∠AOE,
∴∠FOE=∠AOE,∠EOD=∠EOB.
∵∠AOE+∠EOB=180°,
∴∠FOD=∠FOE+∠EOD=(∠AOE+∠EOB)=90°.
∴OF⊥OD.
(2)∵∠AOC:∠AOD=1:5,∠AOC=∠BOD,
∴∠BOD:∠AOD=1:5.
∵∠AOD+∠BOD=180°,
∴∠BOD=30°,∠AOD=150°.
∵OD平分∠BOE,OF平分∠AOE,
∴∠BOE=2∠BOD=60°,∠EOF=∠AOE.
∵∠AOE+∠BOE=180°,
∴∠AOE=120°,
∴∠EOF=60°.
23.解:(1)①∵∠EOF=90°,∠AOE=20°,
∴∠BOF=180°﹣∠EOF﹣∠AOE=70°,
∵OB平分∠COF,
∴∠COF=2∠BOF=140°,
∴∠DOF=180°﹣∠COF=40°,
故答案为:40°,
②∠DOF=2∠AOE,
理由是:设∠AOE=x,
∵∠EOF=90°,
∴∠BOF=180°﹣∠EOF﹣∠AOE=90°﹣x,
∵OB平分∠COF,
∴∠COF=2∠BOF=180°﹣2x,
∴∠DOF=180°﹣∠COF=2x,
∴∠DOF=2∠AOE;
(2)∠DOF=2∠AOE,
理由是:设∠AOE=y,
∵∠EOF=90°,
∴∠BOF=180°﹣∠EOF﹣∠AOE=90°﹣y,
∵OB平分∠COF,
∴∠COF=2∠BOF=180°﹣2y,
∴∠DOF=180°﹣∠COF=2y,
∴∠DOF=2∠AOE.
24.解:(1)①如图所示:
②∵∠BOC=30°,OD平分∠BOC,
∴∠BOD=∠BOC=15°,
∵OD⊥OE,
∴∠DOE=90°,
又∵点O在直线AB上,
∴∠AOE=180°﹣90°﹣15°=75°;
(2)分两种情况:
①当点C在直线AB上方时,如图1,
同理可得,∠BOD=,∠DOE=90°,
∴∠AOE=180°﹣90°﹣=90°﹣;
②当点C在直线AB下方时,如图2,
∵OD平分∠BOC,
∴∠BOD=α,
∵OD⊥OE,
∴∠DOE=90°,
∴∠BOE=90°﹣α,
又∵点O在直线AB上,
∴∠AOE=180°﹣(90°﹣α)=90°+α.
综上所述,∠AOE的度数为90°﹣或90°+α.
25.解:因为两个交点可以形成2对同旁内角,而三个交点形成的同旁内角的对数为6对,
(1)直线l1,l2被直线l3所截,在这个基本图形中,形成了2对同旁内角.
(2)平面内三条直线l1,l2,l3两两相交,交点分别为A、B、C,图中一共有3×2=6对同旁内角.
(3)平面内四条直线两两相交,交点最多为6个,最多可以形成4×(4﹣1)×(4﹣2)=24对同旁内角.
(4)平面内n条直线两两相交,最多可以形成n(n﹣1)(n﹣2)对同旁内角
故答案为:(1)2;(2)6;(3)24;(4)n(n﹣1)(n﹣2)
