山东省淄博市沂源县2021-2022学年七年级上学期期末数学试题(word版含答案)
文档属性
| 名称 | 山东省淄博市沂源县2021-2022学年七年级上学期期末数学试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 768.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-19 22:37:11 | ||
图片预览


文档简介
初二数学试题
本试卷共8页,满分150分,考试时间120分钟.考试结束后,将本试卷和答题卡一并交回.
注意事项:
1.答题前,考生务必用0.5毫米黑色签字笔将学校.姓名.准考证号.考场/座位号填写在答题卡和试卷规定位置,并涂写考试号.
2.选择题每小题选出答案后,用2B铅笔涂黑答题卡对应题目的答案标号;如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.非选择题必须用0.5毫米黑色签字笔作答,字体工整.笔迹清晰,写在答题卡各题目指定区域内;如需改动,先划掉原来答案,然后再写上新答案.严禁使用涂改液.胶带纸.修正带修改.不允许使用计算器.
4.保证答题卡清洁.完整,严禁折叠,严禁在答题卡上做任何标记.
5.评分以答题卡上的答案为依据.不按以上要求作答的答案无效.
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.2是8的
A.平方根 B.立方根 C.算数平方根 D.立方数
2.在中,若斜边,则等于
A.5 B.10 C.20 D.25
3.在平面直角坐标系中,下列各点在第二象限的是
A. B. C. D.
4.在实数,0,,3.1415926,,4.21,中,有理数的个数为
A.3 B.4 C.5 D.6
5.有一个底面为正方形的水池,水池深,容积为,则此水池底面正方形的边长为
A. B. C. D.
6.下列图象中,表示是的函数的个数有
A.1个 B.2个 C.3个 D.4个
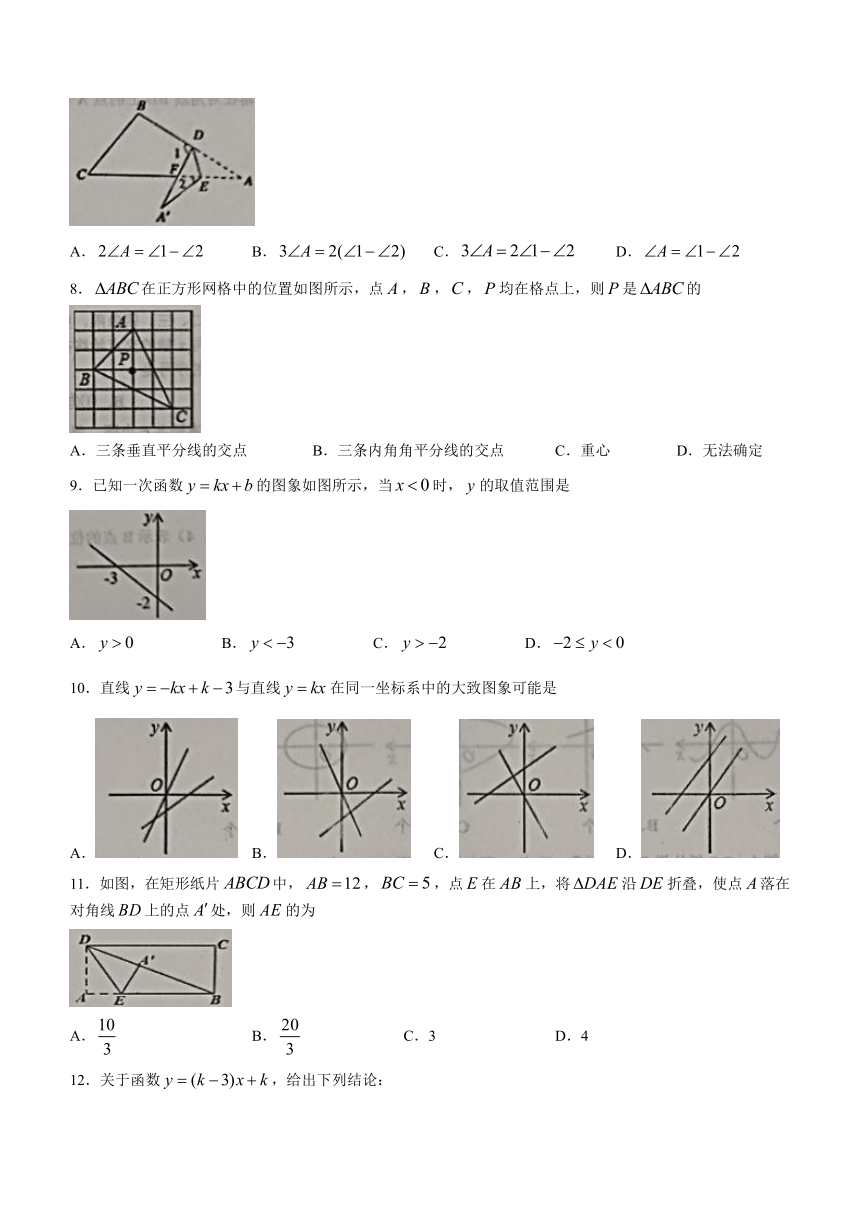
7.如图,把纸片沿折叠,当点落在四边形的外部时,则与和之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是
A. B. C. D.
8.在正方形网格中的位置如图所示,点,,,均在格点上,则是的
A.三条垂直平分线的交点 B.三条内角角平分线的交点 C.重心 D.无法确定
9.已知一次函数的图象如图所示,当时,的取值范围是
A. B. C. D.
10.直线与直线在同一坐标系中的大致图象可能是
A. B. C. D.
11.如图,在矩形纸片中,,,点在上,将沿折叠,使点落在对角线上的点处,则的为
A. B. C.3 D.4
12.关于函数,给出下列结论:
①当时,此函数是一次函数;
②无论取什么值,函数图象必经过点;
③若图象经过二、三、四象限,则的取值范围是;
④若函数图象与轴的交点始终在正半轴,则的取值范围是.
其中正确结论的序号是
A.①②③ B.①③④ C.②③④ D.①②③④
二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果.
13.函数中,自变量的取值范围是________.
14.如图,每个小方格都是边长为1个单位长度的正方形,如果用表示点的位置,用表示点的位置,那么用________表示点的位置.
15.某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参与播种,直至完成800亩的播种任务,播种亩数与天数之间的函数关系如图所示,那么乙播种机参与播种的天数是________天.
16.已知的小数部分为,的小数部分为,则的值是________.
17.如图,小刚站在河边的点处,在河的对面(小刚的正北方向)的处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树处,接着再向前走了30步到达处,然后他左转直行,当小刚看到电线塔.树与自己现处的位置在一条直线时,他一共走了140步.如果小刚一步大约50厘米,估计小刚在点处时他与电线塔的距离________.
三、解答题:本大题共7小题,共70分.解答要写出必要的文字说明、推理过程或演算步骤。
18.(本题满分8分)已知:的平方根是,的立方根是3,求的算术平方根.
19.(本题满分8分)已知图形是一个正方形,图形由三个图形构成.请用图形与合拼成一个轴对称图形,并把它画出来,请画出两个轴对称图形.
20.(本题满分10分)已知一次函数,请按要求解答问题:
(1)为何值时,函数图象过原点,且随的增大而减小?
(2)若函数图象平行于直线,求一次函数解析式;
(3)若点在函数图象上,求的值.
21.(本题满分10分)某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费1.8元,超计划部分每吨按2.0元收费.
(1)写出该单位水费(元)与每月用水量(吨)之间的函数关系式;
①当用水量小于等于3000吨时:________;
②当用水量大于3000吨时:________.
(2)某月该单位用水3200吨,水费是________元;若用水2800吨,水费________元.
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
22.(本题满分10分)如图,在中,点,在上,垂直平分交于点,垂直平分交于点,,,.
(1)求的度数;
(2)求.
23.(本题满分12分)如图,,,.
(1)与全等吗?说明理由;
(2)判断线段与的数量关系,并说明理由.
24.(本题满分12分)如图,直线与轴、轴分别交于点、,点的坐标为,点的坐标为.
(1)求直线的解析式;
(2)若点是第二象限内的直线上的一个动点,在点的运动过程中,试写出的面积与的函数关系式,并写出自变量的取值范围;
(3)探究:在(2)的情况下,当点运动到什么位置时,的面积为,并说明理由.
2021-2022学年第一学期期末考试初二数学参考答案及评分标准
一、选择题:本题共12小题,每小题5分,共60分.
1-12: BDDDA BACCB AD
二、填空题:本题共5小题,每小题4分,共20分.
13.且 14. 15.4 16.1 17.40米
三、解答题:本题共7小题,共70分.
18.解:的平方根是,,
,
的立方根是3,,
把的值代入解得:,
,
的算术平方根为10.
19.解:图略,每个4分,共8分.
20.解:(1)∵一次函数,函数图象过原点,且随的增大而减小,
,且,解
得,,即当时,函数图象过原点,且随的增大而减小
(2)∵一次函数,函数图象平行于直线,,
,
∴一次函数解析式是;
(3)∵点在一次函数的图象上,,
解得,,即的值是.
21.解:(1)当吨时:;
当吨时:.
(2)单位用水3200吨,水费是5800元;
若用水2800吨,水费是5040元.
(3)当该单位缴纳水费9400元,则,
解得.故此时用水5000吨.
22.解:(1)垂直平分,.
垂直平分,.
,,
,,
;
(2)垂直平分,.
垂直平分,.
,,
.
,,,
,,
.
23.解:(1)全等,
理由:,,
在与中,,
(2),
理由:在与中,
,,
,,,
在与中, ,
,.
24.解:(1)∵点在直线上,,
,∴直线的解析式为:;
(2)点在上,设,以为底的边上的高是,因点在第二象限,故,
∵点的坐标为,.
.
点在第二象限,;
(3)的面积为,,
解得,
把代入解析式得,
故点坐标为时,三角形的面积为.
本试卷共8页,满分150分,考试时间120分钟.考试结束后,将本试卷和答题卡一并交回.
注意事项:
1.答题前,考生务必用0.5毫米黑色签字笔将学校.姓名.准考证号.考场/座位号填写在答题卡和试卷规定位置,并涂写考试号.
2.选择题每小题选出答案后,用2B铅笔涂黑答题卡对应题目的答案标号;如需改动,用橡皮擦干净后,再选涂其他答案标号.
3.非选择题必须用0.5毫米黑色签字笔作答,字体工整.笔迹清晰,写在答题卡各题目指定区域内;如需改动,先划掉原来答案,然后再写上新答案.严禁使用涂改液.胶带纸.修正带修改.不允许使用计算器.
4.保证答题卡清洁.完整,严禁折叠,严禁在答题卡上做任何标记.
5.评分以答题卡上的答案为依据.不按以上要求作答的答案无效.
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.2是8的
A.平方根 B.立方根 C.算数平方根 D.立方数
2.在中,若斜边,则等于
A.5 B.10 C.20 D.25
3.在平面直角坐标系中,下列各点在第二象限的是
A. B. C. D.
4.在实数,0,,3.1415926,,4.21,中,有理数的个数为
A.3 B.4 C.5 D.6
5.有一个底面为正方形的水池,水池深,容积为,则此水池底面正方形的边长为
A. B. C. D.
6.下列图象中,表示是的函数的个数有
A.1个 B.2个 C.3个 D.4个
7.如图,把纸片沿折叠,当点落在四边形的外部时,则与和之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是
A. B. C. D.
8.在正方形网格中的位置如图所示,点,,,均在格点上,则是的
A.三条垂直平分线的交点 B.三条内角角平分线的交点 C.重心 D.无法确定
9.已知一次函数的图象如图所示,当时,的取值范围是
A. B. C. D.
10.直线与直线在同一坐标系中的大致图象可能是
A. B. C. D.
11.如图,在矩形纸片中,,,点在上,将沿折叠,使点落在对角线上的点处,则的为
A. B. C.3 D.4
12.关于函数,给出下列结论:
①当时,此函数是一次函数;
②无论取什么值,函数图象必经过点;
③若图象经过二、三、四象限,则的取值范围是;
④若函数图象与轴的交点始终在正半轴,则的取值范围是.
其中正确结论的序号是
A.①②③ B.①③④ C.②③④ D.①②③④
二、填空题:本题共5小题,每小题4分,共20分,只要求填写最后结果.
13.函数中,自变量的取值范围是________.
14.如图,每个小方格都是边长为1个单位长度的正方形,如果用表示点的位置,用表示点的位置,那么用________表示点的位置.
15.某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参与播种,直至完成800亩的播种任务,播种亩数与天数之间的函数关系如图所示,那么乙播种机参与播种的天数是________天.
16.已知的小数部分为,的小数部分为,则的值是________.
17.如图,小刚站在河边的点处,在河的对面(小刚的正北方向)的处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树处,接着再向前走了30步到达处,然后他左转直行,当小刚看到电线塔.树与自己现处的位置在一条直线时,他一共走了140步.如果小刚一步大约50厘米,估计小刚在点处时他与电线塔的距离________.
三、解答题:本大题共7小题,共70分.解答要写出必要的文字说明、推理过程或演算步骤。
18.(本题满分8分)已知:的平方根是,的立方根是3,求的算术平方根.
19.(本题满分8分)已知图形是一个正方形,图形由三个图形构成.请用图形与合拼成一个轴对称图形,并把它画出来,请画出两个轴对称图形.
20.(本题满分10分)已知一次函数,请按要求解答问题:
(1)为何值时,函数图象过原点,且随的增大而减小?
(2)若函数图象平行于直线,求一次函数解析式;
(3)若点在函数图象上,求的值.
21.(本题满分10分)某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费1.8元,超计划部分每吨按2.0元收费.
(1)写出该单位水费(元)与每月用水量(吨)之间的函数关系式;
①当用水量小于等于3000吨时:________;
②当用水量大于3000吨时:________.
(2)某月该单位用水3200吨,水费是________元;若用水2800吨,水费________元.
(3)若某月该单位缴纳水费9400元,则该单位用水多少吨?
22.(本题满分10分)如图,在中,点,在上,垂直平分交于点,垂直平分交于点,,,.
(1)求的度数;
(2)求.
23.(本题满分12分)如图,,,.
(1)与全等吗?说明理由;
(2)判断线段与的数量关系,并说明理由.
24.(本题满分12分)如图,直线与轴、轴分别交于点、,点的坐标为,点的坐标为.
(1)求直线的解析式;
(2)若点是第二象限内的直线上的一个动点,在点的运动过程中,试写出的面积与的函数关系式,并写出自变量的取值范围;
(3)探究:在(2)的情况下,当点运动到什么位置时,的面积为,并说明理由.
2021-2022学年第一学期期末考试初二数学参考答案及评分标准
一、选择题:本题共12小题,每小题5分,共60分.
1-12: BDDDA BACCB AD
二、填空题:本题共5小题,每小题4分,共20分.
13.且 14. 15.4 16.1 17.40米
三、解答题:本题共7小题,共70分.
18.解:的平方根是,,
,
的立方根是3,,
把的值代入解得:,
,
的算术平方根为10.
19.解:图略,每个4分,共8分.
20.解:(1)∵一次函数,函数图象过原点,且随的增大而减小,
,且,解
得,,即当时,函数图象过原点,且随的增大而减小
(2)∵一次函数,函数图象平行于直线,,
,
∴一次函数解析式是;
(3)∵点在一次函数的图象上,,
解得,,即的值是.
21.解:(1)当吨时:;
当吨时:.
(2)单位用水3200吨,水费是5800元;
若用水2800吨,水费是5040元.
(3)当该单位缴纳水费9400元,则,
解得.故此时用水5000吨.
22.解:(1)垂直平分,.
垂直平分,.
,,
,,
;
(2)垂直平分,.
垂直平分,.
,,
.
,,,
,,
.
23.解:(1)全等,
理由:,,
在与中,,
(2),
理由:在与中,
,,
,,,
在与中, ,
,.
24.解:(1)∵点在直线上,,
,∴直线的解析式为:;
(2)点在上,设,以为底的边上的高是,因点在第二象限,故,
∵点的坐标为,.
.
点在第二象限,;
(3)的面积为,,
解得,
把代入解析式得,
故点坐标为时,三角形的面积为.
同课章节目录
