2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的判定与性质 寒假预习同步练习(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学下册6.2矩形的判定与性质 寒假预习同步练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《6-2矩形的判定与性质》
寒假预习同步练习(附答案)
1.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的面积为( )
A.15 B.16 C.22 D.28
2.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
A. B.3 C. D.5
3.如图,矩形ABCD中,AE平分∠BAD交BC于点E,连接DE,若CD=3,DE=5,则AD的长是( )
A.6 B.7 C.8 D.10
4.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE大小是( )
A.55° B.40° C.35° D.20°
5.如图,四边形ABCD是矩形,∠BDC的平分线交AB的延长线于点E,若AD=4,AE=10,则AB的长为( )
A.4.2 B.4.5 C.5.2 D.5.5
6.如图,在矩形ABCD中,AB=1,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C.3 D.
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是( )
A.3 B.5 C.2.4 D.2.5
9.在 ABCD中,若添加一个条件: ,则四边形ABCD是矩形.
10.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
11.如图1,在一张长方形纸片ABCD上画一条线段MN,将纸片沿线段MN折叠(如图2),当∠1=70°时,∠KNC= (注:长方形纸片对边平行,即:CD∥AB,AD∥BC).
12.如图,矩形ABCD的对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若矩形ABCD的周长为8cm,则△ABE的周长为 cm.
13.平行四边形的四个内角平分线相交,如能构成四边形,则这个四边形是 .
14.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
15.如图,矩形ABCD中,AB=12cm,BC=4cm,点P从A 开始沿折线A﹣B﹣A以4cm/s的速度运动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t= 时,四边形APQD也为矩形.
16.如图,矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD是矩形,若△PCD是等腰三角形,则AP的长 .
17.如图,在矩形ABCD中,P为矩形ABCD的边BC上任一点,PE⊥AC于点E,PF⊥BD于点F.若AB=5,BC=12,PE+PF= .
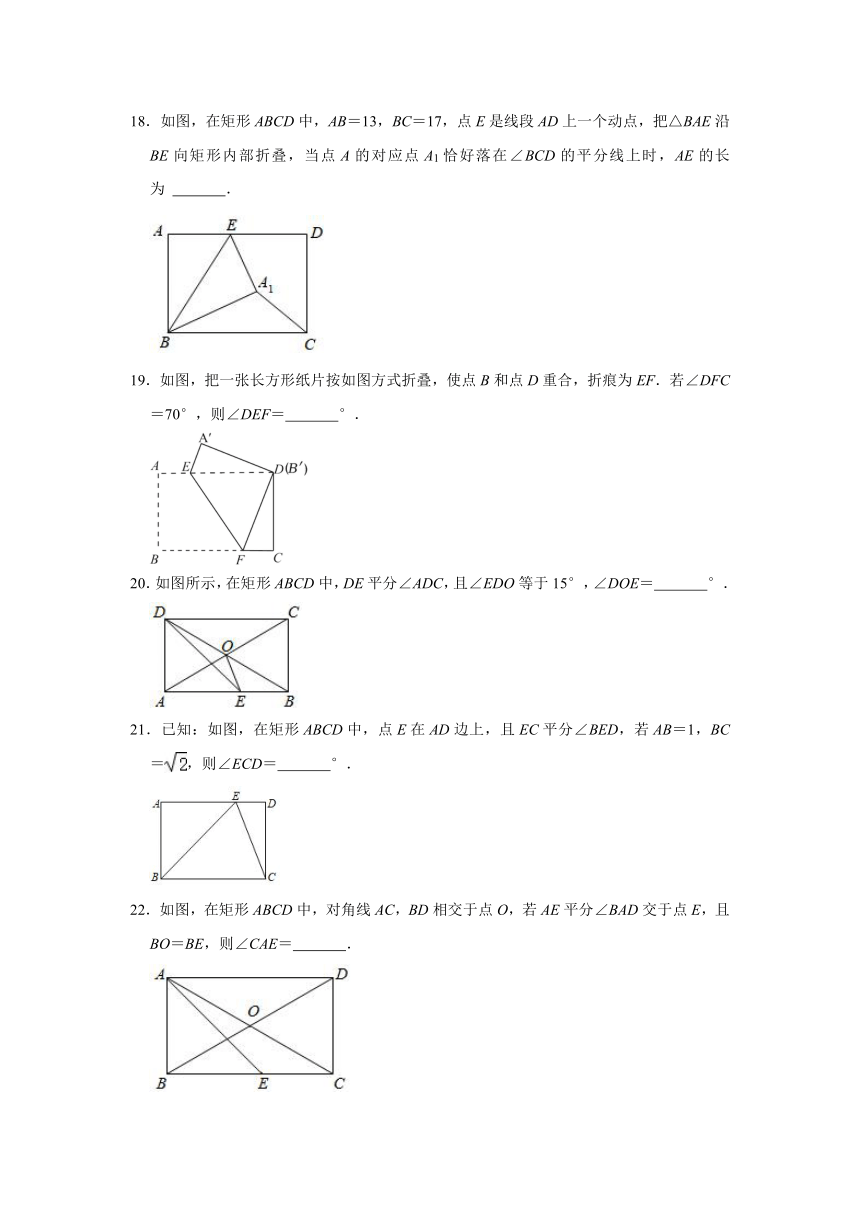
18.如图,在矩形ABCD中,AB=13,BC=17,点E是线段AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,AE的长为 .
19.如图,把一张长方形纸片按如图方式折叠,使点B和点D重合,折痕为EF.若∠DFC=70°,则∠DEF= °.
20.如图所示,在矩形ABCD中,DE平分∠ADC,且∠EDO等于15°,∠DOE= °.
21.已知:如图,在矩形ABCD中,点E在AD边上,且EC平分∠BED,若AB=1,BC=,则∠ECD= °.
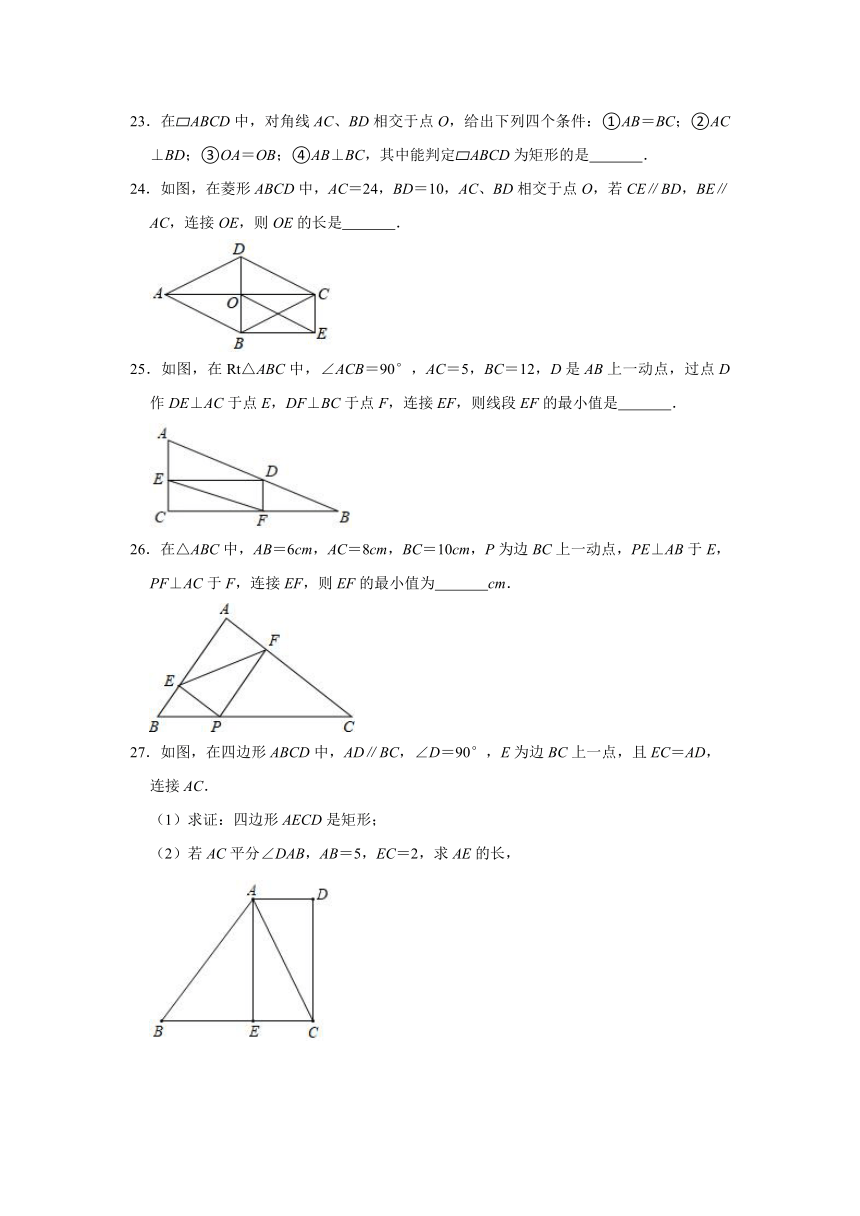
22.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AE平分∠BAD交于点E,且BO=BE,则∠CAE= .
23.在 ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AB=BC;②AC⊥BD;③OA=OB;④AB⊥BC,其中能判定 ABCD为矩形的是 .
24.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE∥BD,BE∥AC,连接OE,则OE的长是 .
25.如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是 .
26.在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为 cm.
27.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连接AC.
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
28.已知,如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=12,∠BCD=120°,求四边形AODE的面积.
29.如图,在 ABCD中,E、F分别是AD、BC的中点,∠AEF的角平分线交AB于点M,∠EFC的角平分线交CD于点N,连接MF、NE.
(1)求证:四边形EMFN是平行四边形.
(2)小明在完成(1)的证明后继续进行了探索,他猜想:当AB=AD时,四边形EMFN是矩形.请在下列框图中补全他的证明思路.
小明的证明思路
由(1)知四边形EMFN是平行四边形.要证 EMFN是矩形,只要证∠MFN=90°.由已知条件知∠EFN=∠CFN,故只要证∠EFM=∠BFM.易证 ,故只要证∠BFM=∠BMF,即证BM=BF,故只要证 .易证AE=AM,AE=BF,即可得证.
30.如图,在菱形ABCD中,点O是对角线AC的中点,过点O的直线EF与边AD、BC交于点E、F,∠CAE=∠FEA,连接AF、CE.
(1)求证:四边形AFCE是矩形;
(2)若AB=5,AC=2,直接写出四边形AFCE的面积.
31.(1)如图①,在四边形ABCD中,∠A=∠C=90°,AB=CD,求证:四边形ABCD是矩形;
(2)如图②,若四边形ABCD满足∠A=∠C>90°,AB=CD,求证:四边形ABCD是平行四边形.
32.如图,已知△OAB中,OA=OB,分别延长AO、BO到点C、D.使得OC=AO,OD=BO,连接AD、DC、CB.
(1)求证:四边形ABCD是矩形;
(2)以OA、OB为一组邻边作 AOBE,连接CE,若CE⊥BD,求∠AOB的度数.
参考答案
1.解:∵四边形ABCD是矩形,
∴AB=DC,AD=BC,∠C=90°,AD∥BC,
∵ED=5,EC=3,
在Rt△DCE中,由勾股定理得:DC==4,
∴AB=DC=4,
∵AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠EAB=∠AEB,
∴BE=AB=4,
∵CE=3,
∴AD=BC=BE+CE=7,
∴矩形ABCD的面积是4×7=28,
故选:D.
2.解:如图,连接AC,OB,
∵四边形AOCB是矩形,
∴AC=OB,
∵点B的坐标是(2,5),点O(0,0),
∴OB==,
∴A,C两点间的距离为,
故选:C.
3.解:∵四边形ABCD是矩形,
∴∠C=90°,AB=CD,AD∥BC,AD=BC,
∵ED=5,CD=3,
∴EC2=DE2﹣CD2=25﹣9=16,
∴CE=4,
∵AD∥BC,
∴∠AEB=∠DAE;
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=CD=3,
∴BC=BE+EC=7,
∴AD=7,
故选:B.
4.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故选:C.
5.解:如图,∵四边形ABCD是矩形,
∴CD∥AB,
∴∠1=∠E.
又∵∠BDC的平分线交AB的延长线于点E,
∴∠1=∠2,
∴∠2=∠E.
∴BE=BD.
∵AE=10,
∴BD=BE=10﹣AB.
在直角△ABD中,AD=4,BD=10﹣AB,则由勾股定理知:AB==.
∴AB=4.2.
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠BAD=90°,OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE=EO,AE⊥BD,
∴AB=AO,
∴OA=AB=OB=1,
∴BD=2,
∴AD===,
故选:B.
7.解:∵四边形ABCD是矩形,
∴OA=OC=OB=OD,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=2,
∴BD=2OB=4,
故选:A.
8.解:连接CE,如图:
在矩形ABCD中,AB=4,BC=8,
∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,
∵OE⊥AC,
∴AE=CE,
设DE=x,则AE=CE=8﹣x,
在Rt△CDE中,由勾股定理得:DE2+DC2=CE2,
∴x2+42=(8﹣x)2,
解得x=3.
∴DE的长为3.
故选:A.
9.解:由题意可得,∠A=90°或∠A=∠B或AC=BD(答案不唯一),
故答案为:∠A=90°或∠A=∠B或AC=BD(答案不唯一).
10.解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
11.解:∵AB∥CD,
∴∠MNK=∠1=70°,
由折叠的性质可得:∠1=∠NMK=70°,
∵CN∥BM,
∴∠CNM+∠KMN=180°,
∴∠CNM=110°,
∴∠KNC=40°,
故答案为:40°.
12.解:∵四边形ABCD是矩形,
∴OB=OD,AB=CD,AD=BC,
∵矩形ABCD的周长为8cm,
∴AB+AD=4cm,
∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=4cm,
故答案为4.
13.解:如图;
∵四边形ABCD是平行四边形,
∴∠DAB+∠ADC=180°;
∵AH、DH平分∠DAB、∠ADC,
∴∠HAD+∠HDA=90°,即∠EHG=90°;
同理可证得:∠HEF=∠EFG=∠FGH=90°;
故四边形EFGH是矩形.
故答案为:矩形.
14.解:如图,连接AP,
∵AB=3,AC=4,BC=5,
∴∠EAF=90°,
∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点.
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵AP BC=AB AC,
∴AP BC=AB AC,
∵AB=3,AC=4,BC=5,
∴5AP=3×4,
∴AP=,
∴AM=;
故答案为:.
15.解:根据题意得:CQ=2t,AP=4t,
则DQ=12﹣2t,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,CD∥AB,
∴当AP=DQ时,四边形APQD是矩形,
即4t=12﹣2t,
解得:t=2,
∴当t=2s时,四边形APQD是矩形;
故答案为:2s.
16.解:在矩形ABCD中,AB=6,AD=8,∠ADC=90°,
∴DC=AB=6,
∴AC===10,
若△PCD是等腰三角形,
①当CP=CD时,AP=AC﹣CP=10﹣6=4;
②当PD=PC时,∠PDC=∠PCD,
∵∠PCD+∠PAD=∠PDC+∠PDA=90°,
∴∠PAD=∠PDA,
∴PD=PA,
∴PA=PC,
∴AP=AC=5,
③当DP=DC时,如图:
过点D作DQ⊥AC于Q,则PQ=CQ,
∵S△ADC=AD DC=AC DQ,
∴DQ===,
∴CQ===,
∴PC=2CQ=,
∴AP=AC﹣PC=10﹣=.
故答案为:4或5或.
17.解:设对角线AC、BD相交于点O,连接PO,
∵矩形ABCD的边AB=5,BC=12,
∴S矩形ABCD=AB BC=5×12=60,
OA=OC,OB=OD,AC=BD,
AC===13,
∴S△BOC=S矩形ABCD=15,OB=OC=AC=,
∴S△BOC=S△BOP+S△POC=OB PF+OC PE=OB(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故答案案为:.
18.解:由翻折的性质可得,A1B=AB=13,A1E=AE,
∵CA1平分∠BCD,∠BCD=90°,
∴∠DCA1=∠BCA1=45°,
过点A1作A1F⊥BC于点F,如图,
则△A1CF是等腰直角三角形,
∴A1F=CF,
设CF=m,则A1F=m,
BF=17﹣m,
在Rt△A1BF中,由勾股定理可得,
A1B2=A1F2+BF2,即132=m2+(17﹣m)2,
解得m=5或m=12,
当m=12时,延长FA1交AD于点G,如图1;
此时A1F=CF=12,BF=5,
∴A1G=FG﹣A1F=1,
设AE=t,则A1E=t,
∵∠A1GE=∠A1FB=90°,∠EA1B=∠A=90°,
∴∠EA1G+∠GEA1=90°,∠BA1F+∠EA1G=90°,
∴∠GEA1=∠BA1F,
∴A1E:A1G=BA1:BF,即t:1=13:5,
∴t=,即AE=;
当m=5时,延长FA1交AD于点G,如图2;
此时A1F=CF=5,BF=12,
∴A1G=FG﹣A1F=8,
设AE=a,则A1E=a,
∵∠A1GE=∠A1FB=90°,∠EA1B=∠A=90°,
∴∠EA1G+∠GEA1=90°,∠BA1F+∠EA1G=90°,
∴∠GEA1=∠BA1F,
∴△A1EG∽△BA1F,
∴A1E:A1G=BA1:BF,即a:8=13:12,
∴a=,即AE=;
故答案为:或.
19.解:如图,由折叠的性质知:∠EFB=∠EFD.
∵∠DFC=70°,∠EFB+∠EFD+∠DFC=180°,
∴∠EFB==55°.
又AD∥BC,
∴∠DEF=∠EFB=55°.
故答案是:55.
20.解:∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AO=CO,BO=DO,AC=BD,
∴OA=OD,
∵DE平分∠ADC
∴∠CDE=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AD=AE,
又∵∠EDO=15°,
∴∠ADO=60°;
∴△OAD是等边三角形,
∴∠AOD=∠OAD=60°,
∴AD=AO=DO,
∴AO=AE,
∴∠AOE=∠AEO,
∵∠OAE=90°﹣∠OAD=30°,
∴∠AOE=∠AEO=(180°﹣30°)=75°,
∴∠DOE=60°+75°=135°,
故答案为:135.
21.解:过点C作CM⊥BE交BE于M,如图,
∵EC平分∠BED,
∴∠CEM=∠CED,
在△EMC和△EDC中
,
∴△EMC≌△EDC(AAS),
∴∠DCE=∠MCE,MC=DC=1,
在Rt△BMC中,BM==1=MC,
∴△BMC为等腰直角三角形,
∴∠MCB=45°,
∴∠MCD=45°
∴∠ECD=∠MCE=22.5°.
故答案为:22.5.
22.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,∠BAD=90°,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵BO=BE,
∴AB=BO=OA,
∴△BAO是等边三角形,
∴∠OAB=60°,
∴∠CAE=∠OAB﹣∠BAE=15°,
故答案为:15°.
23.解:①AB=BC,能利用邻边相等的平行四边形为菱形判定菱形,但不能判定矩形;
②AC⊥BD,能利用对角线垂直的平行四边形是菱形判定菱形,但不能判定矩形;
③OA=OB则能得到AC=BD,能利用对角线相等的平行四边形为矩形判定矩形,正确;
④AB⊥BC,能利用有一个角为直角的平行四边形为矩形判定矩形,正确,
故答案为:③或④.
24.解:∵CE∥BD,BE∥AC,
∴四边形OBEC是平行四边形,
∵四边形ABCD是菱形,
∴OC=OA=AC=12,OB=OD=BD=5,AC⊥BD,
∴∠BOC=90°,
∴BC===13,
∵四边形OBEC是平行四边形,
∴平行四边形OBEC是矩形,
∴OE=BC=13,
故答案为:13.
25.解:如图,连接CD.
∵∠ACB=90°,AC=5,BC=12,
∴AB===13,
∵DE⊥AC,DF⊥BC,∠C=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
此时,S△ABC=BC AC=AB CD,
即×12×5=×13 CD,
解得:CD=,
∴EF=.
故答案为:.
26.解:∵AB=6cm,AC=8cm,BC=10cm,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,∠A=90°,
∵PE⊥AB于E,PF⊥AC于F,
∴∠AEP=∠AFP=90°,
∴四边形AEPF为矩形,
连接AP,如图,EF=AP,当AP的值最小时,EF的值最小,
当AP⊥BC时,AP的值最小,
根据△ABC面积公式,×AB AC=×AP BC,
∴AP===,
∴EF的最小值为.
故答案为.
27.解:(1)证明:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
(2)∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=3.
∴在Rt△ABE中,AE===4.
28.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=×12=6,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=6,
∵四边形ABCD是菱形,
∴OD=OB=6,
∴四边形AODE的面积=OA OD=6×=36
29.(1)证明:在 ABCD中,∠A=∠C,AD∥BC,AD=BC
∵E、F分别是AD、BC的中点,
∴AE=AD,CF=BC
又∵AD=BC,
∴AE=CF,
∵AD∥BC,
∴∠AEF=∠CFE.
∵EM平分∠AEF,FN平分∠EFC.
∴∠AEM=∠FEM=∠AEF,∠CFN=∠FEN=∠CFE.
∵∠AEF=∠CFE,∠AEM=∠AEF,∠CFN=∠CFE.
∴∠AEM=∠CFN,
在△AME和△CNF中,
∴△AME≌△CNF(ASA)
∵∠FEM=∠FEN,
∴EM∥FN,
∵△AME≌△CNF,
∴EM=FN.
∵EM∥FN,EM=FN,
∴四边形EMFN是平行四边形;
(2)解:∠EFM=∠BMF,
AM=BM(或:M是AB中点).
故答案为:∠EFM=∠BMF,AM=BM.
30.(1)证明:∵∠OAE=∠OEA,
∴OA=OE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠OCF=∠OAE,∠OFC=∠OEA,
∴∠OFC=∠OCF,
∵OF=OC,
∵O为AC的中点,
∴OA=OC,
∴OA=OC=OE=OF,
∴四边形AFCE是平行四边形,AC=EF,
∴四边形AFCE是矩形;
(2)解:设CF=x,
∵四边形ABCD是菱形,AB=5,
∴BC=AB=5,
∴BF=5﹣x,
∵四边形AFCE是矩形,
∴∠AFC=90°=∠AFB,
在Rt△AFB和Rt△AFC中,由勾股定理得:AF2=AB2﹣BF2=AC2﹣CF2,
即52﹣(5﹣x)2=(2)2﹣x2,
解得:x=2,
即CF=2,
则AF===4,
∴四边形AFCE的面积是AF×CF=2×4=8.
31.(1)证明:如图①,连接BD,
∵∠A=∠C=90°,
∵AB=CD,BD=DB,
∴Rt△ABD≌Rt△CDB(HL),
∴AD=CB,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴四边形ABCD是矩形;
(2)解:如图②,分别过点B、D作BE⊥AD于点E,DF⊥BC于点F,
∵∠BAD=∠BCD,
∴∠BAE=∠DCF,
∵∠AEB=∠CFD=90°,AB=CD,
∴△ABE≌△CDF(AAS),
∴BE=DF,AE=CF,
由(1)可得四边形EBFD是矩形,
∴ED=BF,
∴AD=BC,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
32.(1)证明:∵OC=AO,OD=BO,
∴四边形ABCD是平行四边形,
∴AO=AC,BO=BD,
∵AO=BO,
∴AC=BD,
∴四边形ABCD是矩形;
(2)解:连接OE,设EC与BD交于F,
∵EC⊥BD,
∴∠CFD=90°,
∵四边形AEBO是平行四边形,
∴AE∥BO,
∴∠AEC=∠CFD=90°,
即△AEC是直角三角形,
∵EO是Rt△AEC中AC边上的中线,
∴EO=AO,
∵四边形AEBO是平行四边形,
∴OB=AE,
∵OA=OB,
∴AE=OA=OE,
∴△AEO是等边三角形,
∴∠OAE=60°,
∵∠OAE+∠AOB=180°,
∴∠AOB=120°.
寒假预习同步练习(附答案)
1.如图,在矩形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的面积为( )
A.15 B.16 C.22 D.28
2.如图,在矩形OABC中,点B的坐标是(2,5),则A,C两点间的距离是( )
A. B.3 C. D.5
3.如图,矩形ABCD中,AE平分∠BAD交BC于点E,连接DE,若CD=3,DE=5,则AD的长是( )
A.6 B.7 C.8 D.10
4.如图,在矩形ABCD中,AC、BD交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE大小是( )
A.55° B.40° C.35° D.20°
5.如图,四边形ABCD是矩形,∠BDC的平分线交AB的延长线于点E,若AD=4,AE=10,则AB的长为( )
A.4.2 B.4.5 C.5.2 D.5.5
6.如图,在矩形ABCD中,AB=1,对角线AC与BD相交于点O,AE⊥BD,垂足为E,若BE=EO,则AD的长是( )
A.3 B. C.3 D.
7.如图,在矩形ABCD中,AB=2,∠AOB=60°,则BD的长为( )
A.4 B.3 C.2 D.2
8.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则DE的长是( )
A.3 B.5 C.2.4 D.2.5
9.在 ABCD中,若添加一个条件: ,则四边形ABCD是矩形.
10.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
11.如图1,在一张长方形纸片ABCD上画一条线段MN,将纸片沿线段MN折叠(如图2),当∠1=70°时,∠KNC= (注:长方形纸片对边平行,即:CD∥AB,AD∥BC).
12.如图,矩形ABCD的对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若矩形ABCD的周长为8cm,则△ABE的周长为 cm.
13.平行四边形的四个内角平分线相交,如能构成四边形,则这个四边形是 .
14.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 .
15.如图,矩形ABCD中,AB=12cm,BC=4cm,点P从A 开始沿折线A﹣B﹣A以4cm/s的速度运动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s),当t= 时,四边形APQD也为矩形.
16.如图,矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD是矩形,若△PCD是等腰三角形,则AP的长 .
17.如图,在矩形ABCD中,P为矩形ABCD的边BC上任一点,PE⊥AC于点E,PF⊥BD于点F.若AB=5,BC=12,PE+PF= .
18.如图,在矩形ABCD中,AB=13,BC=17,点E是线段AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,AE的长为 .
19.如图,把一张长方形纸片按如图方式折叠,使点B和点D重合,折痕为EF.若∠DFC=70°,则∠DEF= °.
20.如图所示,在矩形ABCD中,DE平分∠ADC,且∠EDO等于15°,∠DOE= °.
21.已知:如图,在矩形ABCD中,点E在AD边上,且EC平分∠BED,若AB=1,BC=,则∠ECD= °.
22.如图,在矩形ABCD中,对角线AC,BD相交于点O,若AE平分∠BAD交于点E,且BO=BE,则∠CAE= .
23.在 ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AB=BC;②AC⊥BD;③OA=OB;④AB⊥BC,其中能判定 ABCD为矩形的是 .
24.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE∥BD,BE∥AC,连接OE,则OE的长是 .
25.如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=12,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是 .
26.在△ABC中,AB=6cm,AC=8cm,BC=10cm,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,连接EF,则EF的最小值为 cm.
27.如图,在四边形ABCD中,AD∥BC,∠D=90°,E为边BC上一点,且EC=AD,
连接AC.
(1)求证:四边形AECD是矩形;
(2)若AC平分∠DAB,AB=5,EC=2,求AE的长,
28.已知,如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形;
(2)若AB=12,∠BCD=120°,求四边形AODE的面积.
29.如图,在 ABCD中,E、F分别是AD、BC的中点,∠AEF的角平分线交AB于点M,∠EFC的角平分线交CD于点N,连接MF、NE.
(1)求证:四边形EMFN是平行四边形.
(2)小明在完成(1)的证明后继续进行了探索,他猜想:当AB=AD时,四边形EMFN是矩形.请在下列框图中补全他的证明思路.
小明的证明思路
由(1)知四边形EMFN是平行四边形.要证 EMFN是矩形,只要证∠MFN=90°.由已知条件知∠EFN=∠CFN,故只要证∠EFM=∠BFM.易证 ,故只要证∠BFM=∠BMF,即证BM=BF,故只要证 .易证AE=AM,AE=BF,即可得证.
30.如图,在菱形ABCD中,点O是对角线AC的中点,过点O的直线EF与边AD、BC交于点E、F,∠CAE=∠FEA,连接AF、CE.
(1)求证:四边形AFCE是矩形;
(2)若AB=5,AC=2,直接写出四边形AFCE的面积.
31.(1)如图①,在四边形ABCD中,∠A=∠C=90°,AB=CD,求证:四边形ABCD是矩形;
(2)如图②,若四边形ABCD满足∠A=∠C>90°,AB=CD,求证:四边形ABCD是平行四边形.
32.如图,已知△OAB中,OA=OB,分别延长AO、BO到点C、D.使得OC=AO,OD=BO,连接AD、DC、CB.
(1)求证:四边形ABCD是矩形;
(2)以OA、OB为一组邻边作 AOBE,连接CE,若CE⊥BD,求∠AOB的度数.
参考答案
1.解:∵四边形ABCD是矩形,
∴AB=DC,AD=BC,∠C=90°,AD∥BC,
∵ED=5,EC=3,
在Rt△DCE中,由勾股定理得:DC==4,
∴AB=DC=4,
∵AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠DAB,
∴∠DAE=∠EAB,
∴∠EAB=∠AEB,
∴BE=AB=4,
∵CE=3,
∴AD=BC=BE+CE=7,
∴矩形ABCD的面积是4×7=28,
故选:D.
2.解:如图,连接AC,OB,
∵四边形AOCB是矩形,
∴AC=OB,
∵点B的坐标是(2,5),点O(0,0),
∴OB==,
∴A,C两点间的距离为,
故选:C.
3.解:∵四边形ABCD是矩形,
∴∠C=90°,AB=CD,AD∥BC,AD=BC,
∵ED=5,CD=3,
∴EC2=DE2﹣CD2=25﹣9=16,
∴CE=4,
∵AD∥BC,
∴∠AEB=∠DAE;
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=CD=3,
∴BC=BE+EC=7,
∴AD=7,
故选:B.
4.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD,OA=OC,OB=OD,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠AOD=110°,
∴∠DOE=70°,∠ODC=∠OCD=(180°﹣70°)=55°,
∵DE⊥AC,
∴∠ODE=90°﹣∠DOE=20°,
∴∠CDE=∠ODC﹣∠ODE=55°﹣20°=35°;
故选:C.
5.解:如图,∵四边形ABCD是矩形,
∴CD∥AB,
∴∠1=∠E.
又∵∠BDC的平分线交AB的延长线于点E,
∴∠1=∠2,
∴∠2=∠E.
∴BE=BD.
∵AE=10,
∴BD=BE=10﹣AB.
在直角△ABD中,AD=4,BD=10﹣AB,则由勾股定理知:AB==.
∴AB=4.2.
故选:A.
6.解:∵四边形ABCD是矩形,
∴∠BAD=90°,OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵BE=EO,AE⊥BD,
∴AB=AO,
∴OA=AB=OB=1,
∴BD=2,
∴AD===,
故选:B.
7.解:∵四边形ABCD是矩形,
∴OA=OC=OB=OD,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴OB=AB=2,
∴BD=2OB=4,
故选:A.
8.解:连接CE,如图:
在矩形ABCD中,AB=4,BC=8,
∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,
∵OE⊥AC,
∴AE=CE,
设DE=x,则AE=CE=8﹣x,
在Rt△CDE中,由勾股定理得:DE2+DC2=CE2,
∴x2+42=(8﹣x)2,
解得x=3.
∴DE的长为3.
故选:A.
9.解:由题意可得,∠A=90°或∠A=∠B或AC=BD(答案不唯一),
故答案为:∠A=90°或∠A=∠B或AC=BD(答案不唯一).
10.解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
11.解:∵AB∥CD,
∴∠MNK=∠1=70°,
由折叠的性质可得:∠1=∠NMK=70°,
∵CN∥BM,
∴∠CNM+∠KMN=180°,
∴∠CNM=110°,
∴∠KNC=40°,
故答案为:40°.
12.解:∵四边形ABCD是矩形,
∴OB=OD,AB=CD,AD=BC,
∵矩形ABCD的周长为8cm,
∴AB+AD=4cm,
∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=4cm,
故答案为4.
13.解:如图;
∵四边形ABCD是平行四边形,
∴∠DAB+∠ADC=180°;
∵AH、DH平分∠DAB、∠ADC,
∴∠HAD+∠HDA=90°,即∠EHG=90°;
同理可证得:∠HEF=∠EFG=∠FGH=90°;
故四边形EFGH是矩形.
故答案为:矩形.
14.解:如图,连接AP,
∵AB=3,AC=4,BC=5,
∴∠EAF=90°,
∵PE⊥AB于E,PF⊥AC于F,
∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点.
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵AP BC=AB AC,
∴AP BC=AB AC,
∵AB=3,AC=4,BC=5,
∴5AP=3×4,
∴AP=,
∴AM=;
故答案为:.
15.解:根据题意得:CQ=2t,AP=4t,
则DQ=12﹣2t,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,CD∥AB,
∴当AP=DQ时,四边形APQD是矩形,
即4t=12﹣2t,
解得:t=2,
∴当t=2s时,四边形APQD是矩形;
故答案为:2s.
16.解:在矩形ABCD中,AB=6,AD=8,∠ADC=90°,
∴DC=AB=6,
∴AC===10,
若△PCD是等腰三角形,
①当CP=CD时,AP=AC﹣CP=10﹣6=4;
②当PD=PC时,∠PDC=∠PCD,
∵∠PCD+∠PAD=∠PDC+∠PDA=90°,
∴∠PAD=∠PDA,
∴PD=PA,
∴PA=PC,
∴AP=AC=5,
③当DP=DC时,如图:
过点D作DQ⊥AC于Q,则PQ=CQ,
∵S△ADC=AD DC=AC DQ,
∴DQ===,
∴CQ===,
∴PC=2CQ=,
∴AP=AC﹣PC=10﹣=.
故答案为:4或5或.
17.解:设对角线AC、BD相交于点O,连接PO,
∵矩形ABCD的边AB=5,BC=12,
∴S矩形ABCD=AB BC=5×12=60,
OA=OC,OB=OD,AC=BD,
AC===13,
∴S△BOC=S矩形ABCD=15,OB=OC=AC=,
∴S△BOC=S△BOP+S△POC=OB PF+OC PE=OB(PE+PF)=××(PE+PF)=15,
∴PE+PF=,
故答案案为:.
18.解:由翻折的性质可得,A1B=AB=13,A1E=AE,
∵CA1平分∠BCD,∠BCD=90°,
∴∠DCA1=∠BCA1=45°,
过点A1作A1F⊥BC于点F,如图,
则△A1CF是等腰直角三角形,
∴A1F=CF,
设CF=m,则A1F=m,
BF=17﹣m,
在Rt△A1BF中,由勾股定理可得,
A1B2=A1F2+BF2,即132=m2+(17﹣m)2,
解得m=5或m=12,
当m=12时,延长FA1交AD于点G,如图1;
此时A1F=CF=12,BF=5,
∴A1G=FG﹣A1F=1,
设AE=t,则A1E=t,
∵∠A1GE=∠A1FB=90°,∠EA1B=∠A=90°,
∴∠EA1G+∠GEA1=90°,∠BA1F+∠EA1G=90°,
∴∠GEA1=∠BA1F,
∴A1E:A1G=BA1:BF,即t:1=13:5,
∴t=,即AE=;
当m=5时,延长FA1交AD于点G,如图2;
此时A1F=CF=5,BF=12,
∴A1G=FG﹣A1F=8,
设AE=a,则A1E=a,
∵∠A1GE=∠A1FB=90°,∠EA1B=∠A=90°,
∴∠EA1G+∠GEA1=90°,∠BA1F+∠EA1G=90°,
∴∠GEA1=∠BA1F,
∴△A1EG∽△BA1F,
∴A1E:A1G=BA1:BF,即a:8=13:12,
∴a=,即AE=;
故答案为:或.
19.解:如图,由折叠的性质知:∠EFB=∠EFD.
∵∠DFC=70°,∠EFB+∠EFD+∠DFC=180°,
∴∠EFB==55°.
又AD∥BC,
∴∠DEF=∠EFB=55°.
故答案是:55.
20.解:∵四边形ABCD是矩形,
∴∠ADC=∠BAD=90°,AO=CO,BO=DO,AC=BD,
∴OA=OD,
∵DE平分∠ADC
∴∠CDE=∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AD=AE,
又∵∠EDO=15°,
∴∠ADO=60°;
∴△OAD是等边三角形,
∴∠AOD=∠OAD=60°,
∴AD=AO=DO,
∴AO=AE,
∴∠AOE=∠AEO,
∵∠OAE=90°﹣∠OAD=30°,
∴∠AOE=∠AEO=(180°﹣30°)=75°,
∴∠DOE=60°+75°=135°,
故答案为:135.
21.解:过点C作CM⊥BE交BE于M,如图,
∵EC平分∠BED,
∴∠CEM=∠CED,
在△EMC和△EDC中
,
∴△EMC≌△EDC(AAS),
∴∠DCE=∠MCE,MC=DC=1,
在Rt△BMC中,BM==1=MC,
∴△BMC为等腰直角三角形,
∴∠MCB=45°,
∴∠MCD=45°
∴∠ECD=∠MCE=22.5°.
故答案为:22.5.
22.解:∵四边形ABCD是矩形,
∴AC=BD,OA=OC=AC,OB=OD=BD,∠BAD=90°,
∴OA=OB,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,
∵BO=BE,
∴AB=BO=OA,
∴△BAO是等边三角形,
∴∠OAB=60°,
∴∠CAE=∠OAB﹣∠BAE=15°,
故答案为:15°.
23.解:①AB=BC,能利用邻边相等的平行四边形为菱形判定菱形,但不能判定矩形;
②AC⊥BD,能利用对角线垂直的平行四边形是菱形判定菱形,但不能判定矩形;
③OA=OB则能得到AC=BD,能利用对角线相等的平行四边形为矩形判定矩形,正确;
④AB⊥BC,能利用有一个角为直角的平行四边形为矩形判定矩形,正确,
故答案为:③或④.
24.解:∵CE∥BD,BE∥AC,
∴四边形OBEC是平行四边形,
∵四边形ABCD是菱形,
∴OC=OA=AC=12,OB=OD=BD=5,AC⊥BD,
∴∠BOC=90°,
∴BC===13,
∵四边形OBEC是平行四边形,
∴平行四边形OBEC是矩形,
∴OE=BC=13,
故答案为:13.
25.解:如图,连接CD.
∵∠ACB=90°,AC=5,BC=12,
∴AB===13,
∵DE⊥AC,DF⊥BC,∠C=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
此时,S△ABC=BC AC=AB CD,
即×12×5=×13 CD,
解得:CD=,
∴EF=.
故答案为:.
26.解:∵AB=6cm,AC=8cm,BC=10cm,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,∠A=90°,
∵PE⊥AB于E,PF⊥AC于F,
∴∠AEP=∠AFP=90°,
∴四边形AEPF为矩形,
连接AP,如图,EF=AP,当AP的值最小时,EF的值最小,
当AP⊥BC时,AP的值最小,
根据△ABC面积公式,×AB AC=×AP BC,
∴AP===,
∴EF的最小值为.
故答案为.
27.解:(1)证明:∵AD∥BC,EC=AD,
∴四边形AECD是平行四边形.
又∵∠D=90°,
∴四边形AECD是矩形.
(2)∵AC平分∠DAB.
∴∠BAC=∠DAC.
∵AD∥BC,
∴∠DAC=∠ACB.
∴∠BAC=∠ACB.
∴BA=BC=5.
∵EC=2,
∴BE=3.
∴在Rt△ABE中,AE===4.
28.(1)证明:∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
故四边形AODE是矩形;
(2)解:∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=×12=6,
∵在菱形ABCD中,AC⊥BD
∴由勾股定理OB=6,
∵四边形ABCD是菱形,
∴OD=OB=6,
∴四边形AODE的面积=OA OD=6×=36
29.(1)证明:在 ABCD中,∠A=∠C,AD∥BC,AD=BC
∵E、F分别是AD、BC的中点,
∴AE=AD,CF=BC
又∵AD=BC,
∴AE=CF,
∵AD∥BC,
∴∠AEF=∠CFE.
∵EM平分∠AEF,FN平分∠EFC.
∴∠AEM=∠FEM=∠AEF,∠CFN=∠FEN=∠CFE.
∵∠AEF=∠CFE,∠AEM=∠AEF,∠CFN=∠CFE.
∴∠AEM=∠CFN,
在△AME和△CNF中,
∴△AME≌△CNF(ASA)
∵∠FEM=∠FEN,
∴EM∥FN,
∵△AME≌△CNF,
∴EM=FN.
∵EM∥FN,EM=FN,
∴四边形EMFN是平行四边形;
(2)解:∠EFM=∠BMF,
AM=BM(或:M是AB中点).
故答案为:∠EFM=∠BMF,AM=BM.
30.(1)证明:∵∠OAE=∠OEA,
∴OA=OE,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠OCF=∠OAE,∠OFC=∠OEA,
∴∠OFC=∠OCF,
∵OF=OC,
∵O为AC的中点,
∴OA=OC,
∴OA=OC=OE=OF,
∴四边形AFCE是平行四边形,AC=EF,
∴四边形AFCE是矩形;
(2)解:设CF=x,
∵四边形ABCD是菱形,AB=5,
∴BC=AB=5,
∴BF=5﹣x,
∵四边形AFCE是矩形,
∴∠AFC=90°=∠AFB,
在Rt△AFB和Rt△AFC中,由勾股定理得:AF2=AB2﹣BF2=AC2﹣CF2,
即52﹣(5﹣x)2=(2)2﹣x2,
解得:x=2,
即CF=2,
则AF===4,
∴四边形AFCE的面积是AF×CF=2×4=8.
31.(1)证明:如图①,连接BD,
∵∠A=∠C=90°,
∵AB=CD,BD=DB,
∴Rt△ABD≌Rt△CDB(HL),
∴AD=CB,
∴四边形ABCD是平行四边形,
∵∠A=90°,
∴四边形ABCD是矩形;
(2)解:如图②,分别过点B、D作BE⊥AD于点E,DF⊥BC于点F,
∵∠BAD=∠BCD,
∴∠BAE=∠DCF,
∵∠AEB=∠CFD=90°,AB=CD,
∴△ABE≌△CDF(AAS),
∴BE=DF,AE=CF,
由(1)可得四边形EBFD是矩形,
∴ED=BF,
∴AD=BC,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形.
32.(1)证明:∵OC=AO,OD=BO,
∴四边形ABCD是平行四边形,
∴AO=AC,BO=BD,
∵AO=BO,
∴AC=BD,
∴四边形ABCD是矩形;
(2)解:连接OE,设EC与BD交于F,
∵EC⊥BD,
∴∠CFD=90°,
∵四边形AEBO是平行四边形,
∴AE∥BO,
∴∠AEC=∠CFD=90°,
即△AEC是直角三角形,
∵EO是Rt△AEC中AC边上的中线,
∴EO=AO,
∵四边形AEBO是平行四边形,
∴OB=AE,
∵OA=OB,
∴AE=OA=OE,
∴△AEO是等边三角形,
∴∠OAE=60°,
∵∠OAE+∠AOB=180°,
∴∠AOB=120°.
