山东省菏泽市2021-2022学年高三上学期期末考试数学试题(A)(扫描版含答案)
文档属性
| 名称 | 山东省菏泽市2021-2022学年高三上学期期末考试数学试题(A)(扫描版含答案) | 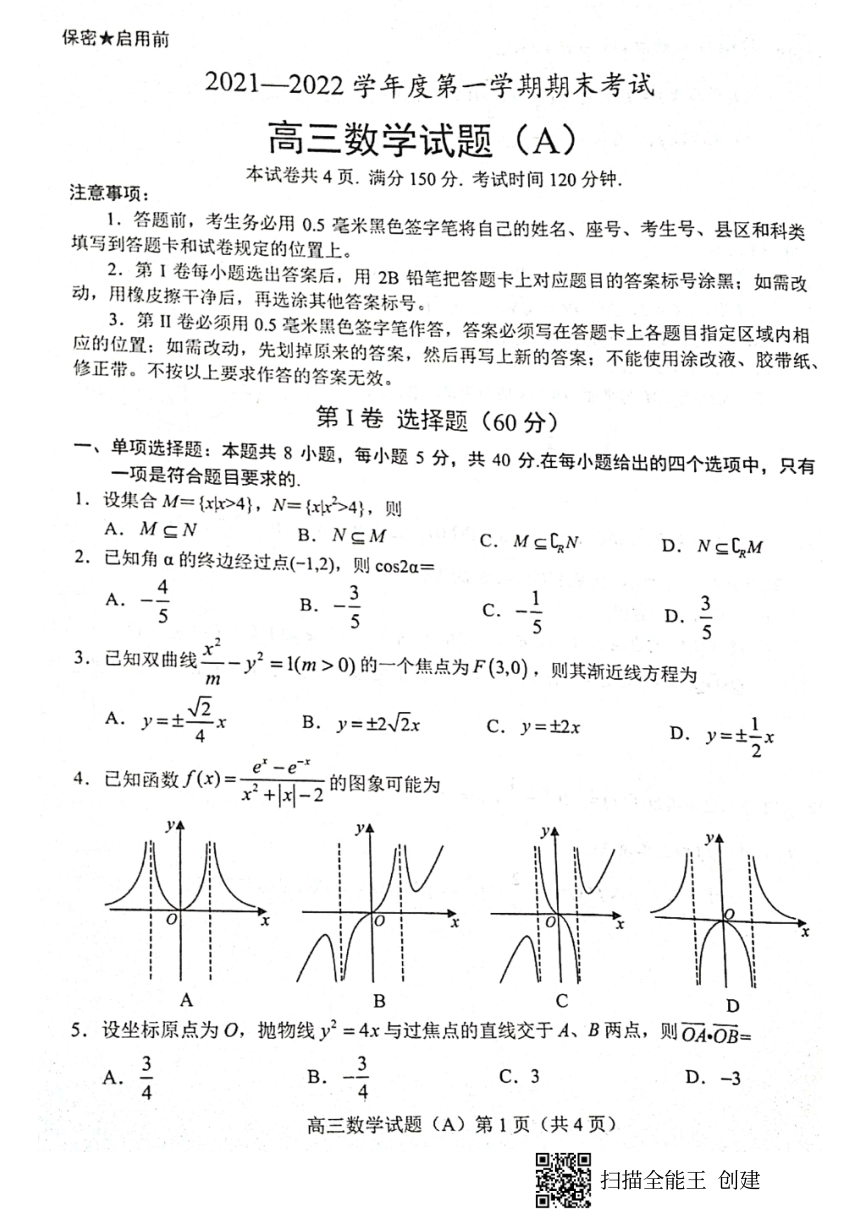 | |
| 格式 | |||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 20:25:51 | ||
图片预览





文档简介
保密★启用前
2021—2022学年度第一学期期末考试
高三数学试题(A)
本试卷共4页.满分150分.考试时间120分钟
注意事项:
1.答题前,考生务必用05毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类
填写到答题卡和试卷规定的位置上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改
动,用橡皮擦干净后,再选涂其他答案标号
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡上各题目指定区域内相
应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸
修正带。不按以上要求作答的答案无效
第I卷选择题(60分)
、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有
项是符合题目要求的
1.设集合M={xx>4},N={xx2>4},则
A. McN
B. NCM
2.已知角α的终边经过点(-1,2),则cos2u=
D. N ct,M
D
=m>0的一个焦点为F(,则其渐近线方程为
3.已知双曲线
B
y=±
已知函数∫(x)
x2+|x-2
的图象可能为
B
C
D
5.设坐标原点为O,抛物线y2=4x与过焦点的直线交于A、B两点,则OAOB=
B
高三数学试题(A)第1页(共4页)
6.已知三棱柱ABC-A1B1C1的底面是边长为2的等边三角形
侧棱长为3,A1在底面ABC上的射影D为BC的中点,则
异面直线AB与CC1所成的角的为
B1
元—6元-3
x-4元2
D
设函数∫(x),g(x)的定义域分别为F,G,且FcG.若对任意的x∈F,都有
g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数
已知函数∫(x)=e(x≤0),
若g(x)为f(x)在R上的一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是
A
B. In
8.瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线
上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC,
点B(-1,1),点C(3,5),过其“欧拉线”上一点P作圆O:x2+y2=4的两条切线,切点
分别为M,N,则N的最小值为
A
2
C
二、多项选择题:本题共4小题,每小题5分,共20分在每小题给出的四个选项中,有多
项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分
9.设m,n是两条不同的直线,a,β是两个不同的平面,且直线mc平面a,直线nc平面
β,下列命题为真命题的是
A.“a∥β”是“m∥β”的充分条件B.“m∥n”是“m∥β”的必要条件
C.“n⊥a”是“m⊥n”的充要条件D.“m⊥n”是“a⊥β”的既不充分也不必要条件
10.已知曲线C
4-mm-2
l(m∈R),则下列说法正确的是
若2B.若m>4,则曲线C为焦点在y轴上的双曲线
C.若曲线C为双曲线,则其焦距是定值
D.若曲线C为焦点在x轴上的双曲线,则其离心率小于2
11设m≠0,若x==m为函数∫(x)=-m(x+m)(x+n)的极大值点,则下列关系中可能成
立的有
A
n-n
B. n>m>0
C. nD. m>n>0
12.函数f(x)=~b
(a>0,b>0)的图象类似于汉字“囧”字,被称为“囧函数”,并把
其与y轴的交点关于原点的对称点称为“囹点”,以“囧点”为圆心,凡是与“囧函数”
有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,下列结论正确的是
A.函数∫(x)的图象关于直线x=1对称
B.当x∈(-1,1)时,∫(x)的最大值为-1
C.函数f(x)的“点”与函数y=lnx图象上的点的最短距离为√2
D.函数∫(x)的所有“囧圆”中,面积的最小值为3
高三数学试题(A)第2页(共4页
2021—2022学年度第一学期期末考试
高三数学试题(A)
本试卷共4页.满分150分.考试时间120分钟
注意事项:
1.答题前,考生务必用05毫米黑色签字笔将自己的姓名、座号、考生号、县区和科类
填写到答题卡和试卷规定的位置上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改
动,用橡皮擦干净后,再选涂其他答案标号
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡上各题目指定区域内相
应的位置;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸
修正带。不按以上要求作答的答案无效
第I卷选择题(60分)
、单项选择题:本题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有
项是符合题目要求的
1.设集合M={xx>4},N={xx2>4},则
A. McN
B. NCM
2.已知角α的终边经过点(-1,2),则cos2u=
D. N ct,M
D
=m>0的一个焦点为F(,则其渐近线方程为
3.已知双曲线
B
y=±
已知函数∫(x)
x2+|x-2
的图象可能为
B
C
D
5.设坐标原点为O,抛物线y2=4x与过焦点的直线交于A、B两点,则OAOB=
B
高三数学试题(A)第1页(共4页)
6.已知三棱柱ABC-A1B1C1的底面是边长为2的等边三角形
侧棱长为3,A1在底面ABC上的射影D为BC的中点,则
异面直线AB与CC1所成的角的为
B1
元—6元-3
x-4元2
D
设函数∫(x),g(x)的定义域分别为F,G,且FcG.若对任意的x∈F,都有
g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数
已知函数∫(x)=e(x≤0),
若g(x)为f(x)在R上的一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是
A
B. In
8.瑞士著名数学家欧拉在1765年提出定理:三角形的外心、重心、垂心位于同一直线
上.这条直线被后人称为三角形的“欧拉线”.在平面直角坐标系中作△ABC,AB=AC,
点B(-1,1),点C(3,5),过其“欧拉线”上一点P作圆O:x2+y2=4的两条切线,切点
分别为M,N,则N的最小值为
A
2
C
二、多项选择题:本题共4小题,每小题5分,共20分在每小题给出的四个选项中,有多
项符合题目要求全部选对的得5分,部分选对的得2分,有选错的得0分
9.设m,n是两条不同的直线,a,β是两个不同的平面,且直线mc平面a,直线nc平面
β,下列命题为真命题的是
A.“a∥β”是“m∥β”的充分条件B.“m∥n”是“m∥β”的必要条件
C.“n⊥a”是“m⊥n”的充要条件D.“m⊥n”是“a⊥β”的既不充分也不必要条件
10.已知曲线C
4-mm-2
l(m∈R),则下列说法正确的是
若2
C.若曲线C为双曲线,则其焦距是定值
D.若曲线C为焦点在x轴上的双曲线,则其离心率小于2
11设m≠0,若x==m为函数∫(x)=-m(x+m)(x+n)的极大值点,则下列关系中可能成
立的有
A
n-n
B. n>m>0
C. n
12.函数f(x)=~b
(a>0,b>0)的图象类似于汉字“囧”字,被称为“囧函数”,并把
其与y轴的交点关于原点的对称点称为“囹点”,以“囧点”为圆心,凡是与“囧函数”
有公共点的圆,皆称之为“囧圆”,则当a=1,b=1时,下列结论正确的是
A.函数∫(x)的图象关于直线x=1对称
B.当x∈(-1,1)时,∫(x)的最大值为-1
C.函数f(x)的“点”与函数y=lnx图象上的点的最短距离为√2
D.函数∫(x)的所有“囧圆”中,面积的最小值为3
高三数学试题(A)第2页(共4页
同课章节目录
