人教版七年级数学 下册 第七章 7.2.1 用坐标表示地理位置 同步练习题(含答案)
文档属性
| 名称 | 人教版七年级数学 下册 第七章 7.2.1 用坐标表示地理位置 同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 343.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 19:26:45 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第七章 平面直角坐标系
7.2.1 用坐标表示地理位置
一、选择题
1.如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为(D)
A.(2,3) B.(0,3)
C.(3,2) D.(2,2)
2.确定一个点的位置,下列说法正确的是( )
A.偏东10°,100米 B.东南方向
C.距这里150米 D.由此向南100米
3.如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见:一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,2)。另有情报得知:指挥部坐标为(0,0),你认为敌军指挥部的位置大约是( )
A.A处 B.B处
C.C处 D.D处
4.如图是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )
A.(2,3),(3,2)
B.(3,2),(2,3)
C.(2,3),(-3,2)
D.(3,2),(-2,3)
5.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
填空题
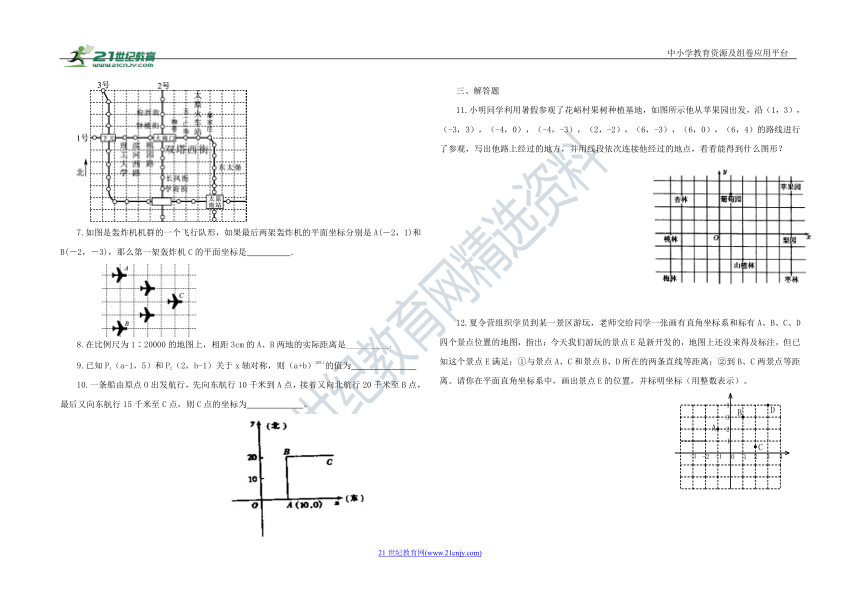
6.如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是 .
7.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是 .
8.在比例尺为1∶20000的地图上,相距3cm的A、B两地的实际距离是__________.
9.已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2011的值为
10.一条船由原点O出发航行,先向东航行10千米到A点,接着又向北航行20千米至B点,最后又向东航行15千米至C点,则C点的坐标为 。
三、解答题
11.小明同学利用暑假参观了花峪村果树种植基地,如图所示他从苹果园出发,沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(6,-3),(6,0),(6,4)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点,看看能得到什么图形?
12.夏令营组织学员到某一景区游玩,老师交给同学一张画有直角坐标系和标有A、B、C、D 四个景点位置的地图,指出:今天我们游玩的景点E是新开发的,地图上还没来得及标注,但已知这个景点E满足:①与景点A、C和景点B、D所在的两条直线等距离;②到B、C两景点等距离。请你在平面直角坐标系中,画出景点E的位置,并标明坐标(用整数表示)。
13.某次海战中敌我双方舰艇对峙示意图(图中1 cm代表20海里)如下,对我方潜艇O来说:
(1)北偏东40°的方向上有哪些目标?要想确定敌舰B的位置,还需要什么数据?
(2)距离我方潜艇20海里的敌舰有哪几艘?
(3)要确定每艘敌舰的位置,各需要几个数据?
14.如上图,这是某市部分简图,请以火车站为坐标原点建立平面直角坐标系, 并分别写出各地的坐标.
15.
15.小明的爷爷退休生活可丰富了!下表是他某日的活动安排.和平广场位于爷爷家东400米,老年大学位于爷爷家西600米.从爷爷家到和平路小学需先向南走300米,再向西走400米.请依据图示中给定的单位长度,在图中标出和平广场A、老年大学B与和平路小学C的位置.
早晨6:00~7:00 与奶奶一起到和平广场锻炼
上午9:00~11:00 与奶奶一起上老年大学
下午4:30~5:30 到和平路小学讲校史
16.在A市北300km处有B市,以A市为原点,东西方向的直线为x轴,南北方向的直线为y轴,并以50km为1个单位建立平面直角坐标系.根据气象台预报,今年7号台风中心位置现在C(10,6)处,并以40千米/时的速度自东向西移动,台风影响范围半径为200km,问经几小时后,B市将受到台风影响 并画出示意图.
17.在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥Ox,且点N到极点O的距离为4个单位长度,求点N的极坐标.
18.数学世界
奔跑的狗
苏步青是我国著名数学家、教育家,历任复旦大家教授、校长等职.1995年当选为中国科学院学部委员.苏步青的主要研究领域是微分几何学,他又是优秀的教学教育家,从事数学教学达60年,培养了大批数学人才.
一次在德国,苏步青与一位有名的数学家同乘电车时,这位数学家出了一道题目给苏教授解答.
这道题是:
甲乙两人同时从相距100千米的两地出发,相向而行,甲每小时走6千米,乙每小时走4千米,甲带了一只狗和他同时出发,狗以每小时10千米的速度向乙奔去,遇到乙即回头向甲奔去;遇到甲又回头向乙奔去,直到甲乙两人相遇时狗才停住.问这只狗共奔跑了多少千米路?
对这个问题,苏步青教授略加思索,就算出了正确的答案.请你也想一想,该怎么解答?
参考答案:
一、1.D 2.D 3.B 4.D 5.B
二、6.(3,0)
7.(2,-1)
8.600米
9.-1 .
10.(25,20)
三、11.经过的地方是:葡萄园、杏林、桃林、梅林、山楂林、枣林、梨园、苹果园。
画图答案如图所示:
作图略
13.解:(1)对我方潜艇来说,北偏东40°的方向上有两个目标,敌舰B和小岛.要想确定敌舰B的位置,还需要知道敌舰B距我方潜艇的距离.
(2)距离我方潜艇20海里的敌舰有两艘,敌舰A和敌舰C.
(3)要确定每艘敌舰的位置,各需要两个数据:距离和方位角.
14.图略:火车站(0,0),医院(– 2,– 2),文化宫(– 3,1),体育场
(– 4,3),宾馆(2,2),市场(4,3),超市(2,– 3)
如上右图.A点为和平广场,B点为老年大家,C点为和平路小学.
16.提示:50×6÷40=7.5(小时).所以经过7.5小时后,B市将受到台风的影响.
(注:图中的单位1表示50km)
17.(4,90°)
18. 甲、乙两人从出发到相遇共用100÷(6+4)=10(小时),在这段时间内,狗一直奔跑着,所以这只狗共奔跑了10×10=100(千米)路.
21世纪教育网(www.21cnjy.com)
第七章 平面直角坐标系
7.2.1 用坐标表示地理位置
一、选择题
1.如图,若以解放公园为原点建立平面直角坐标系,则博物馆的坐标为(D)
A.(2,3) B.(0,3)
C.(3,2) D.(2,2)
2.确定一个点的位置,下列说法正确的是( )
A.偏东10°,100米 B.东南方向
C.距这里150米 D.由此向南100米
3.如图所示,某战役缴获敌人防御工事坐标地图碎片,依稀可见:一号暗堡的坐标为(4,2),四号暗堡的坐标为(-2,2)。另有情报得知:指挥部坐标为(0,0),你认为敌军指挥部的位置大约是( )
A.A处 B.B处
C.C处 D.D处
4.如图是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( )
A.(2,3),(3,2)
B.(3,2),(2,3)
C.(2,3),(-3,2)
D.(3,2),(-2,3)
5.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是( )
A.点A B.点B C.点C D.点D
填空题
6.如图是利用网格画出的太原市地铁1,2,3号线路部分规划示意图,若建立适当的平面直角坐标系,表示双塔西街点的坐标为(0,-1),表示桃园路的点的坐标为(-1,0),则表示太原火车站的点(正好在网格点上)的坐标是 .
7.如图是轰炸机机群的一个飞行队形,如果最后两架轰炸机的平面坐标分别是A(-2,1)和B(-2,-3),那么第一架轰炸机C的平面坐标是 .
8.在比例尺为1∶20000的地图上,相距3cm的A、B两地的实际距离是__________.
9.已知P1(a-1,5)和P2(2,b-1)关于x轴对称,则(a+b)2011的值为
10.一条船由原点O出发航行,先向东航行10千米到A点,接着又向北航行20千米至B点,最后又向东航行15千米至C点,则C点的坐标为 。
三、解答题
11.小明同学利用暑假参观了花峪村果树种植基地,如图所示他从苹果园出发,沿(1,3),(-3,3),(-4,0),(-4,-3),(2,-2),(6,-3),(6,0),(6,4)的路线进行了参观,写出他路上经过的地方,并用线段依次连接他经过的地点,看看能得到什么图形?
12.夏令营组织学员到某一景区游玩,老师交给同学一张画有直角坐标系和标有A、B、C、D 四个景点位置的地图,指出:今天我们游玩的景点E是新开发的,地图上还没来得及标注,但已知这个景点E满足:①与景点A、C和景点B、D所在的两条直线等距离;②到B、C两景点等距离。请你在平面直角坐标系中,画出景点E的位置,并标明坐标(用整数表示)。
13.某次海战中敌我双方舰艇对峙示意图(图中1 cm代表20海里)如下,对我方潜艇O来说:
(1)北偏东40°的方向上有哪些目标?要想确定敌舰B的位置,还需要什么数据?
(2)距离我方潜艇20海里的敌舰有哪几艘?
(3)要确定每艘敌舰的位置,各需要几个数据?
14.如上图,这是某市部分简图,请以火车站为坐标原点建立平面直角坐标系, 并分别写出各地的坐标.
15.
15.小明的爷爷退休生活可丰富了!下表是他某日的活动安排.和平广场位于爷爷家东400米,老年大学位于爷爷家西600米.从爷爷家到和平路小学需先向南走300米,再向西走400米.请依据图示中给定的单位长度,在图中标出和平广场A、老年大学B与和平路小学C的位置.
早晨6:00~7:00 与奶奶一起到和平广场锻炼
上午9:00~11:00 与奶奶一起上老年大学
下午4:30~5:30 到和平路小学讲校史
16.在A市北300km处有B市,以A市为原点,东西方向的直线为x轴,南北方向的直线为y轴,并以50km为1个单位建立平面直角坐标系.根据气象台预报,今年7号台风中心位置现在C(10,6)处,并以40千米/时的速度自东向西移动,台风影响范围半径为200km,问经几小时后,B市将受到台风影响 并画出示意图.
17.在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向).对于平面内任何一点M,用ρ表示线段OM的长度,θ表示从Ox到OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫点M的极坐标,若ON⊥Ox,且点N到极点O的距离为4个单位长度,求点N的极坐标.
18.数学世界
奔跑的狗
苏步青是我国著名数学家、教育家,历任复旦大家教授、校长等职.1995年当选为中国科学院学部委员.苏步青的主要研究领域是微分几何学,他又是优秀的教学教育家,从事数学教学达60年,培养了大批数学人才.
一次在德国,苏步青与一位有名的数学家同乘电车时,这位数学家出了一道题目给苏教授解答.
这道题是:
甲乙两人同时从相距100千米的两地出发,相向而行,甲每小时走6千米,乙每小时走4千米,甲带了一只狗和他同时出发,狗以每小时10千米的速度向乙奔去,遇到乙即回头向甲奔去;遇到甲又回头向乙奔去,直到甲乙两人相遇时狗才停住.问这只狗共奔跑了多少千米路?
对这个问题,苏步青教授略加思索,就算出了正确的答案.请你也想一想,该怎么解答?
参考答案:
一、1.D 2.D 3.B 4.D 5.B
二、6.(3,0)
7.(2,-1)
8.600米
9.-1 .
10.(25,20)
三、11.经过的地方是:葡萄园、杏林、桃林、梅林、山楂林、枣林、梨园、苹果园。
画图答案如图所示:
作图略
13.解:(1)对我方潜艇来说,北偏东40°的方向上有两个目标,敌舰B和小岛.要想确定敌舰B的位置,还需要知道敌舰B距我方潜艇的距离.
(2)距离我方潜艇20海里的敌舰有两艘,敌舰A和敌舰C.
(3)要确定每艘敌舰的位置,各需要两个数据:距离和方位角.
14.图略:火车站(0,0),医院(– 2,– 2),文化宫(– 3,1),体育场
(– 4,3),宾馆(2,2),市场(4,3),超市(2,– 3)
如上右图.A点为和平广场,B点为老年大家,C点为和平路小学.
16.提示:50×6÷40=7.5(小时).所以经过7.5小时后,B市将受到台风的影响.
(注:图中的单位1表示50km)
17.(4,90°)
18. 甲、乙两人从出发到相遇共用100÷(6+4)=10(小时),在这段时间内,狗一直奔跑着,所以这只狗共奔跑了10×10=100(千米)路.
21世纪教育网(www.21cnjy.com)
