湖南省邵阳市隆回县2021-2022学年九年级上学期期末考试数学试题(word版、含答案)
文档属性
| 名称 | 湖南省邵阳市隆回县2021-2022学年九年级上学期期末考试数学试题(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 298.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 14:43:56 | ||
图片预览



文档简介
2021年下期九年级期末考试试题卷
数 学
温馨提示:
1.本学科试卷分试题卷和答题卡两部分;
2.请你将自己的姓名、准考证号等相关信息按要求填涂在答题卡上;
3.请你在答题卡上作答,做在本试题卷上的答案无效。
一、选择题(共10个小题,每小题3分,共30分,每小题只有一个选项正确)
1. 如果反比例函数(是常数)的图象在第一、三象限,那么的取值范围是:
A.>0 B. <0 C. >1 D. <1
2. 下列方程是一元二次方程的是:
A. B.
C. D.
3. 下列四个数成比例的是:
A. 3,9,5,15 B. 1,2,3,4 C. 2,4,5,8 D. 3,5,7,9
4. 在Rt△ABC中,∠C=90o,AC=6,BC=8,则sinA=
A. B. C. D.
5. 在一次中考模拟考试中,随机抽取了部分学生的数学成绩作为样本,成绩在100分以上的频率为0.15,于是可估计全校500名参加中考模拟考试的学生中数学成绩在100分以上学生人数为:
A. 150人 B. 75人 C. 50人 D. 15人
6. 若,是一元二次方程的两个实数根,的值是:
A. -1 B. 1 C.-11 D. 11
7. 如图,△ABC中,∠ACB=90o,∠CAB=30o,CD⊥AB于D,CD=2,则BC=
A. B.
C. D. 4
8. 如图,在△ABC中,AC⊥BC,∠ABC=30o,AC=1,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为:
A. B.
C. D.
9. 反比例函数与一次函数的图象的交点个数是:
A. 3 B. 2 C. 1 D. 0
10. 如图,∠ABD=∠BDC=90o,∠A=∠CBD,AB=3,BD=2,则CD的长为:
A. B. C. 2 D. 3
二、填空题(共10个小题,每小题3分,共30分)
11. 反比例函数的图象经过点(3,3),则的值为: 。
12. 已知关于的一元二次方程的一个根为-1,则它的另一个根为 。
13. 如图,在ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于 。
14. 如图,在Rt△ABC中,∠C=90o,BC=3,AB=5,则tanA= 。
15. 已知一组数据0,1,2,,3的平均数是2,则的值为 。
16. 质检部门从1500件电子产品中随机抽取了100件进行检测,其中有3件是次品,据此可估计这批电子产品中大约有 件次品。
17. 如图,在△ABC中,MN∥BC,已知AM=2,MB=4,BC=6,则MN的长为 。
18. 如图,河坝的横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=6m,则坡面AB的长度是 m。
19. 如图,DE∥BC,△ADE的面积等于△ABC面积的一半,则 。
20. 已知,是关于的一元二次方程的两个实数根,且,则的值为 。
三、解答题(见答题卡第21—26题)
三、解答题(21~24小题每题6分,25,26小题每题8分,共40分,答题时要写出解答过程)
21. (6分)(1)计算:
(2)解方程:
22.(6分)若关于的一元二次方程有两个不相等的实数根。
(1)求的取值范围;
(2)若是方程的一个实数根,求实数的值。(结果保留根号)
23.(6分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长。(结果保留根号)
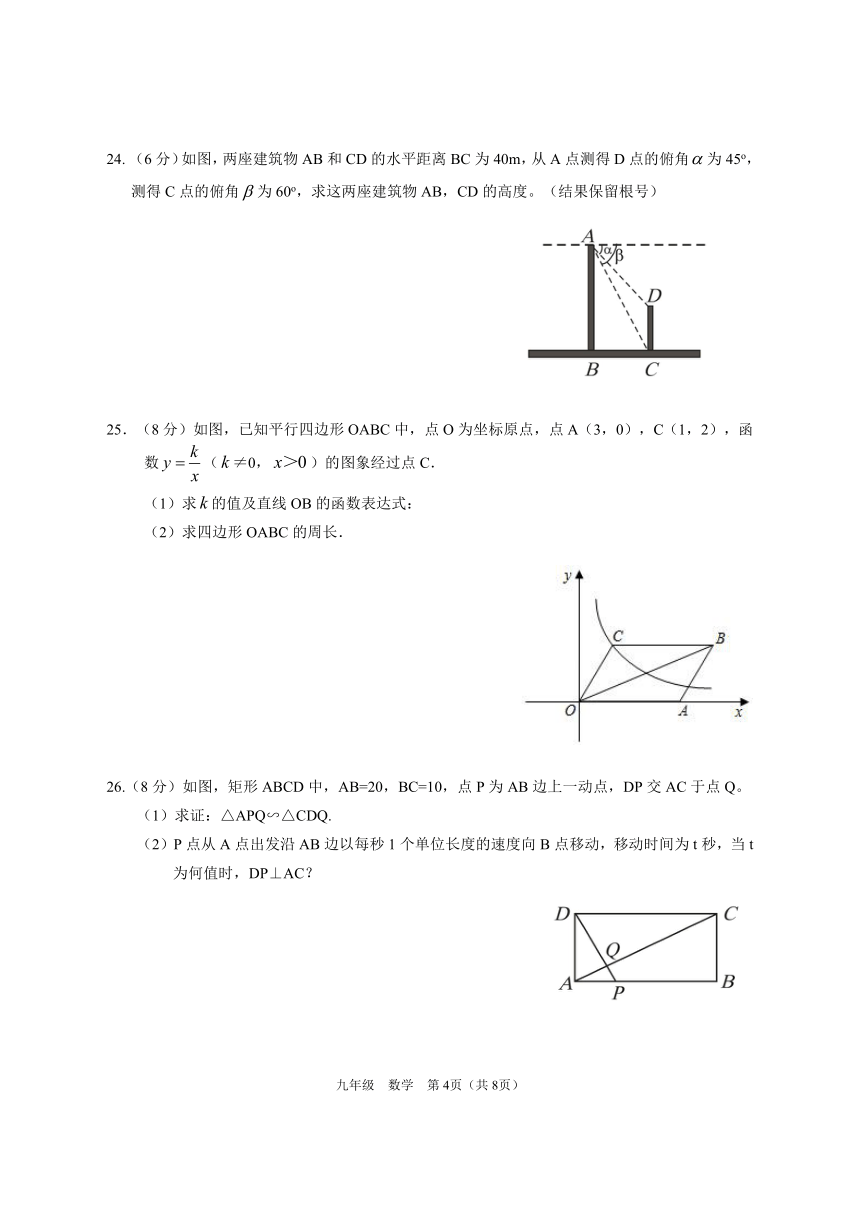
(6分)如图,两座建筑物AB和CD的水平距离BC为40m,从A点测得D点的俯角为45o,测得C点的俯角为60o,求这两座建筑物AB,CD的高度。(结果保留根号)
25.(8分)如图,已知平行四边形OABC中,点O为坐标原点,点A(3,0),C(1,2),函数(≠0,)的图象经过点C.
(1)求的值及直线OB的函数表达式:
(2)求四边形OABC的周长.
26.(8分)如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q。
(1)求证:△APQ∽△CDQ.
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒,当t为何值时,DP⊥AC?
2021年下期九年级期末考试
数学参考答案
一、选择题(10'×3=30')
CBACB DBACA
二、填空题(10'×3=30')
11. 5; 12. -2; 13. (或1:2); 14. ; 15. 4;
16. 45; 17. 2; 18. 12; 19. (或); 20. .
三、解答题(21~24小题每题6分,25~26小题每题8分,共40分)
21. (1)解:原式(2分)(3分)
(2)原方程可化为:(2分)
解得:,(3分)
解:(1)由△(1分)
解得: (3分)
把代入方程
并整理得:(4分)
配方得 (5分)
解得 , 满足.(6分)
(1)∵ABCD是矩形,∴∠B=90o,AD∥BC,∴∠AEB=∠DAF(1分)
又∵DF⊥AE,∴∠DFA=90o,∴∠B=∠DFA(2分)
在△ABE和△DFA中,∠B=∠DFA=90o,∠AEB=∠DAF,∴△ABE∽△DFA(3分)
(其它方法参照给分)
(2)由(1)知△ABE∽△DFA,∴(4分)在Rt△ABE中.
AB=6 BE=2 ∴(5分)
∴(6分)
解:在Rt△ABC中,∠ABC=90o,BC=40m,∠ACB==60o
∴AB=BC×tan60o=40(m)(3分)
过D作DE⊥AB于点E,在Rt△AED中,∠AED=90o,∠ADE==45o
∴ AE=DE=40,∴ DC=BE=AB-AE=40-40(m)
∴ 两座建筑物AB高为40m,AD高为40(-1)m.(6分)
解:(1)依题意有:点C(1,2)在反比例函数y(k≠0)的图象上,
∴k=xy=2,(2分)
∵A(3,0)
∴CB=OA=3,
又CB∥x轴,
∴B(4,2),(3分)
设直线OB的函数表达式为y=ax,
∴2=4a,
∴a,
∴直线OB的函数表达式为y x;(5分)
(2)作CD⊥OA于点D,
∵C(1,2),
∴OC,(7分)
在平行四边形OABC中,
CB=OA=3,AB=OC,
∴四边形OABC的周长为:3+36+2,(8分)
即四边形OABC的周长为6+2.
解(1)∵ABCD为矩形,∴AB∥CD ∴∠QAP=∠DCQ,∠CDQ=∠QPA
又 ∠DQC=∠PQA ∴△APQ∽△CDQ(3分)
(2)当DP⊥AC时,有∠QAP+∠QPA=90o,又∵∠QAP+∠QAD=90o
∴∠DAC=∠DPA,又∠DAP=∠ADC=90o
∴△DAP∽△CDA(5分) ∴
∴(7分) ∴(秒)
∴时,DP⊥AC(8分)
九年级 数学 第1页(共3页)
数 学
温馨提示:
1.本学科试卷分试题卷和答题卡两部分;
2.请你将自己的姓名、准考证号等相关信息按要求填涂在答题卡上;
3.请你在答题卡上作答,做在本试题卷上的答案无效。
一、选择题(共10个小题,每小题3分,共30分,每小题只有一个选项正确)
1. 如果反比例函数(是常数)的图象在第一、三象限,那么的取值范围是:
A.>0 B. <0 C. >1 D. <1
2. 下列方程是一元二次方程的是:
A. B.
C. D.
3. 下列四个数成比例的是:
A. 3,9,5,15 B. 1,2,3,4 C. 2,4,5,8 D. 3,5,7,9
4. 在Rt△ABC中,∠C=90o,AC=6,BC=8,则sinA=
A. B. C. D.
5. 在一次中考模拟考试中,随机抽取了部分学生的数学成绩作为样本,成绩在100分以上的频率为0.15,于是可估计全校500名参加中考模拟考试的学生中数学成绩在100分以上学生人数为:
A. 150人 B. 75人 C. 50人 D. 15人
6. 若,是一元二次方程的两个实数根,的值是:
A. -1 B. 1 C.-11 D. 11
7. 如图,△ABC中,∠ACB=90o,∠CAB=30o,CD⊥AB于D,CD=2,则BC=
A. B.
C. D. 4
8. 如图,在△ABC中,AC⊥BC,∠ABC=30o,AC=1,点D是CB延长线上的一点,且BD=BA,则tan∠DAC的值为:
A. B.
C. D.
9. 反比例函数与一次函数的图象的交点个数是:
A. 3 B. 2 C. 1 D. 0
10. 如图,∠ABD=∠BDC=90o,∠A=∠CBD,AB=3,BD=2,则CD的长为:
A. B. C. 2 D. 3
二、填空题(共10个小题,每小题3分,共30分)
11. 反比例函数的图象经过点(3,3),则的值为: 。
12. 已知关于的一元二次方程的一个根为-1,则它的另一个根为 。
13. 如图,在ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于 。
14. 如图,在Rt△ABC中,∠C=90o,BC=3,AB=5,则tanA= 。
15. 已知一组数据0,1,2,,3的平均数是2,则的值为 。
16. 质检部门从1500件电子产品中随机抽取了100件进行检测,其中有3件是次品,据此可估计这批电子产品中大约有 件次品。
17. 如图,在△ABC中,MN∥BC,已知AM=2,MB=4,BC=6,则MN的长为 。
18. 如图,河坝的横断面迎水坡AB的坡比是(坡比是坡面的铅直高度BC与水平宽度AC之比),坝高BC=6m,则坡面AB的长度是 m。
19. 如图,DE∥BC,△ADE的面积等于△ABC面积的一半,则 。
20. 已知,是关于的一元二次方程的两个实数根,且,则的值为 。
三、解答题(见答题卡第21—26题)
三、解答题(21~24小题每题6分,25,26小题每题8分,共40分,答题时要写出解答过程)
21. (6分)(1)计算:
(2)解方程:
22.(6分)若关于的一元二次方程有两个不相等的实数根。
(1)求的取值范围;
(2)若是方程的一个实数根,求实数的值。(结果保留根号)
23.(6分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证:△ABE∽△DFA;
(2)若AB=6,BC=4,求DF的长。(结果保留根号)
(6分)如图,两座建筑物AB和CD的水平距离BC为40m,从A点测得D点的俯角为45o,测得C点的俯角为60o,求这两座建筑物AB,CD的高度。(结果保留根号)
25.(8分)如图,已知平行四边形OABC中,点O为坐标原点,点A(3,0),C(1,2),函数(≠0,)的图象经过点C.
(1)求的值及直线OB的函数表达式:
(2)求四边形OABC的周长.
26.(8分)如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q。
(1)求证:△APQ∽△CDQ.
(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒,当t为何值时,DP⊥AC?
2021年下期九年级期末考试
数学参考答案
一、选择题(10'×3=30')
CBACB DBACA
二、填空题(10'×3=30')
11. 5; 12. -2; 13. (或1:2); 14. ; 15. 4;
16. 45; 17. 2; 18. 12; 19. (或); 20. .
三、解答题(21~24小题每题6分,25~26小题每题8分,共40分)
21. (1)解:原式(2分)(3分)
(2)原方程可化为:(2分)
解得:,(3分)
解:(1)由△(1分)
解得: (3分)
把代入方程
并整理得:(4分)
配方得 (5分)
解得 , 满足.(6分)
(1)∵ABCD是矩形,∴∠B=90o,AD∥BC,∴∠AEB=∠DAF(1分)
又∵DF⊥AE,∴∠DFA=90o,∴∠B=∠DFA(2分)
在△ABE和△DFA中,∠B=∠DFA=90o,∠AEB=∠DAF,∴△ABE∽△DFA(3分)
(其它方法参照给分)
(2)由(1)知△ABE∽△DFA,∴(4分)在Rt△ABE中.
AB=6 BE=2 ∴(5分)
∴(6分)
解:在Rt△ABC中,∠ABC=90o,BC=40m,∠ACB==60o
∴AB=BC×tan60o=40(m)(3分)
过D作DE⊥AB于点E,在Rt△AED中,∠AED=90o,∠ADE==45o
∴ AE=DE=40,∴ DC=BE=AB-AE=40-40(m)
∴ 两座建筑物AB高为40m,AD高为40(-1)m.(6分)
解:(1)依题意有:点C(1,2)在反比例函数y(k≠0)的图象上,
∴k=xy=2,(2分)
∵A(3,0)
∴CB=OA=3,
又CB∥x轴,
∴B(4,2),(3分)
设直线OB的函数表达式为y=ax,
∴2=4a,
∴a,
∴直线OB的函数表达式为y x;(5分)
(2)作CD⊥OA于点D,
∵C(1,2),
∴OC,(7分)
在平行四边形OABC中,
CB=OA=3,AB=OC,
∴四边形OABC的周长为:3+36+2,(8分)
即四边形OABC的周长为6+2.
解(1)∵ABCD为矩形,∴AB∥CD ∴∠QAP=∠DCQ,∠CDQ=∠QPA
又 ∠DQC=∠PQA ∴△APQ∽△CDQ(3分)
(2)当DP⊥AC时,有∠QAP+∠QPA=90o,又∵∠QAP+∠QAD=90o
∴∠DAC=∠DPA,又∠DAP=∠ADC=90o
∴△DAP∽△CDA(5分) ∴
∴(7分) ∴(秒)
∴时,DP⊥AC(8分)
九年级 数学 第1页(共3页)
同课章节目录
