2021--2022学年人教版七年级数学下册5.4 平移 同步练习题(word版含答案)
文档属性
| 名称 | 2021--2022学年人教版七年级数学下册5.4 平移 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 07:30:18 | ||
图片预览


文档简介
第五章 相交线与平行线
5.4 平移
一、选择题
1.下列哪个图形是由左图平移得到的( )
2.如图所示,△DEF经过平移可以得到△ABC,那么∠C
的对应角和ED的对应边分-别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
3.如图,把边长为2的正方形的局部进行如图①~图④的变换,拼成图⑤,则图⑤的面积是( ).
A 18 B 16 C 12 D 8
4.如图,平移后得到,则和对应的线段是( )
A 、 B、 C、 D、以上都不对
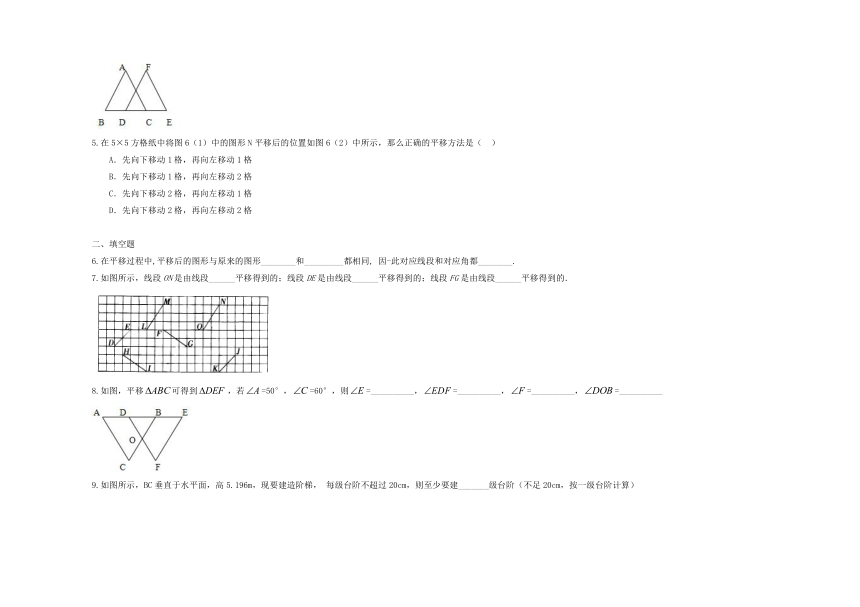
5.在5×5方格纸中将图6(1)中的图形N平移后的位置如图6(2)中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
填空题
6.在平移过程中,平移后的图形与原来的图形________和_________都相同,因-此对应线段和对应角都________.
7.如图所示,线段ON是由线段______平移得到的;线段DE是由线段______平移得到的;线段FG是由线段______平移得到的.
8.如图,平移可得到,若=50°,=60°,则=__________,=__________,=__________,=__________
9.如图所示,BC垂直于水平面,高5.196m,现要建造阶梯,每级台阶不超过20cm,则至少要建_______级台阶(不足20cm,按一级台阶计算)
10.直角△ABC中,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为____cm2。
三、解答题
11.如图7所示,在网格中,有三角形ABC,将A点平移到P点,画出三角形ABC平移后的图形.
[解答]
(1)将A点向_______(或向______)平移______格(或_____格).
(2)再向_____(或向_____)平移______格(或_______格),得点P.
(3)同理B,C与A点平移次数方向距离一样,易得B′,C′.
(4)连结PB′,PC′,B′C′得到三角形ABC平移后的三角形PB′C′.
12.如图:把△ABC平移得到△DEF,使点A移动到点D ,画出平移后的△DEF。
13.如图,若要在长32m,宽20m的长方形地面上修筑同样宽2米的两条道路,余下的部分修草坪,草坪的面积是多少?
14.如图,将沿方向平移距离得到,已知=5,=8,=3,求图中阴影部分面积。
15.如图所示,一块边长为8米的正方形土地,上面修了横竖各两条道路,宽都是1米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积?
16.如图:将△ABC沿着从B到D的方向平移后得到△EDF,若AB=4㎝ AE=3㎝ CE=1㎝
⑴指出平移的距离是多少
⑵求线段BD,DE的长
17.河的两岸成平行线,A,B是位于河两岸的两个车间(如图).要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法如下:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB.EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.试说出桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.
18.一宾馆准备在大厅的主楼梯上铺设一种红地毯,已知地毯40元/米2,主楼梯的宽为2米,其侧面如图所示,则地毯至少需要多少元?
参考答案:
一、1.C 2.C 3.B 4.C 5.C
二、6.大小、形状、相等
7.LM,KJ,HI.
8.70 , 50 , 60 60
9.26(点拨:=26)
10.12
三、11.2,c 5.3(或2),2(或3)
12.作图略
13. 540m2
14.S阴= S梯形BGFE= (5+8)×5=
15.将两条道路平移得到如图所示,则空白面积为(8-2)(8-2)=36(m2)
思路点拨:运用平移思想方法是求这类面积问题最佳途径.
16.3㎝,BD=3㎝ DE=4㎝
17.利用图形平移的性质及连接两点的线中,线段最短,可知:AC+CD+DB=(ED+DB)+CD=EB+CD.而CD的长度又是平行线PQ与MN之间的距离,所以AC+CD+DB最短.
18.672元
5.4 平移
一、选择题
1.下列哪个图形是由左图平移得到的( )
2.如图所示,△DEF经过平移可以得到△ABC,那么∠C
的对应角和ED的对应边分-别是( )
A.∠F,AC B.∠BOD,BA; C.∠F,BA D.∠BOD,AC
3.如图,把边长为2的正方形的局部进行如图①~图④的变换,拼成图⑤,则图⑤的面积是( ).
A 18 B 16 C 12 D 8
4.如图,平移后得到,则和对应的线段是( )
A 、 B、 C、 D、以上都不对
5.在5×5方格纸中将图6(1)中的图形N平移后的位置如图6(2)中所示,那么正确的平移方法是( )
A.先向下移动1格,再向左移动1格
B.先向下移动1格,再向左移动2格
C.先向下移动2格,再向左移动1格
D.先向下移动2格,再向左移动2格
填空题
6.在平移过程中,平移后的图形与原来的图形________和_________都相同,因-此对应线段和对应角都________.
7.如图所示,线段ON是由线段______平移得到的;线段DE是由线段______平移得到的;线段FG是由线段______平移得到的.
8.如图,平移可得到,若=50°,=60°,则=__________,=__________,=__________,=__________
9.如图所示,BC垂直于水平面,高5.196m,现要建造阶梯,每级台阶不超过20cm,则至少要建_______级台阶(不足20cm,按一级台阶计算)
10.直角△ABC中,AC=3cm,BC=4cm,AB=5cm,将△ABC沿CB方向平移3cm,则边AB所经过的平面面积为____cm2。
三、解答题
11.如图7所示,在网格中,有三角形ABC,将A点平移到P点,画出三角形ABC平移后的图形.
[解答]
(1)将A点向_______(或向______)平移______格(或_____格).
(2)再向_____(或向_____)平移______格(或_______格),得点P.
(3)同理B,C与A点平移次数方向距离一样,易得B′,C′.
(4)连结PB′,PC′,B′C′得到三角形ABC平移后的三角形PB′C′.
12.如图:把△ABC平移得到△DEF,使点A移动到点D ,画出平移后的△DEF。
13.如图,若要在长32m,宽20m的长方形地面上修筑同样宽2米的两条道路,余下的部分修草坪,草坪的面积是多少?
14.如图,将沿方向平移距离得到,已知=5,=8,=3,求图中阴影部分面积。
15.如图所示,一块边长为8米的正方形土地,上面修了横竖各两条道路,宽都是1米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积?
16.如图:将△ABC沿着从B到D的方向平移后得到△EDF,若AB=4㎝ AE=3㎝ CE=1㎝
⑴指出平移的距离是多少
⑵求线段BD,DE的长
17.河的两岸成平行线,A,B是位于河两岸的两个车间(如图).要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短.确定桥的位置的方法如下:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB.EB交MN于D.在D处作到对岸的垂线DC,那么DC就是造桥的位置.试说出桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.
18.一宾馆准备在大厅的主楼梯上铺设一种红地毯,已知地毯40元/米2,主楼梯的宽为2米,其侧面如图所示,则地毯至少需要多少元?
参考答案:
一、1.C 2.C 3.B 4.C 5.C
二、6.大小、形状、相等
7.LM,KJ,HI.
8.70 , 50 , 60 60
9.26(点拨:=26)
10.12
三、11.2,c 5.3(或2),2(或3)
12.作图略
13. 540m2
14.S阴= S梯形BGFE= (5+8)×5=
15.将两条道路平移得到如图所示,则空白面积为(8-2)(8-2)=36(m2)
思路点拨:运用平移思想方法是求这类面积问题最佳途径.
16.3㎝,BD=3㎝ DE=4㎝
17.利用图形平移的性质及连接两点的线中,线段最短,可知:AC+CD+DB=(ED+DB)+CD=EB+CD.而CD的长度又是平行线PQ与MN之间的距离,所以AC+CD+DB最短.
18.672元
