2021-2022学年北师大版八年级数学下册1.4角的平分线 同步自主达标测评(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册1.4角的平分线 同步自主达标测评(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 299.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 07:43:31 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学下册《1-4角的平分线》同步自主达标测评(附答案)
一.选择题(共9小题,满分36分)
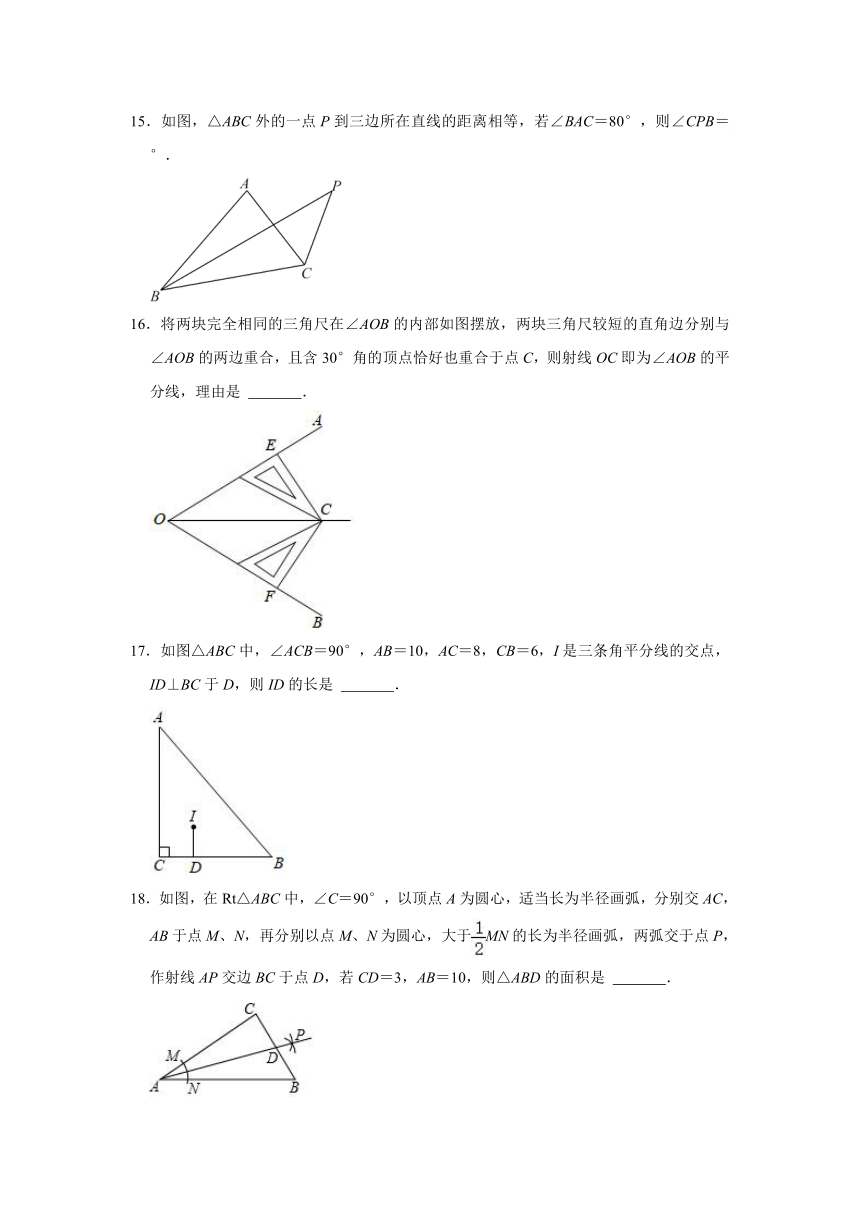
1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.2 B.3 C.4 D.5
2.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E.若AC=10,DE=4,则AD的长为( )
A.2 B.4 C.6 D.8
3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若S△ACD=6,AC=6,则点D到AB的距离为( )
A.1 B.2 C.3 D.4
4.如图,∠AOB=150°,OP平分∠AOB,PD⊥OB于点D,PC∥OB交OA于点C,若PD=3,则OC的长为( )
A.3 B.4 C.5 D.6
5.为了加快灾后重建的步伐,我市某镇要在三条公路围成的一块平地上修建一个砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址( )
A.仅有一处 B.有四处 C.有七处 D.有无数处
6.如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点D,过点C作CG⊥AB于点G,交AD于点E,过点D作DF⊥AB于点F.下列结论:
①∠B=∠ACG;②CE=DF;
③∠CED=∠CDE;
④S△AEC:S△AEG=AC:AG.
上述结论中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
7.如图,OC平分∠AOB,点P在OC上,且PD⊥OB,垂足为D,若PD=3cm,则P到OA的距离d满足( )
A.d<3cm B.d=3cm C.d>3cm D.无法确定
8.有下列四种说法:①角的内部任意一点到角的两边的距离相等;②到角的两边距离相等的点在这个角的平分线上;③角的平分线上任意一点到角的两边的距离相等;④在△ABC中的∠BAC的平分线上任意一点到三角形三边的距离相等,其中正确的有( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,AB=8,BC=9,AC=6,AD是角平分线,DE⊥AB,DF⊥AC,则S△ABD:S△ACD=( )
A.4:3 B.9:8 C.9:6 D.3:2
二.填空题(共10小题,满分40分)
10.如图,在△ABC中,O是△ABC内一点,且点O到△ABC三边的距离相等,∠BOC=126°,则∠A的度数为 .
11.如图所示,BD是∠ABC的平分线,DE⊥AB于点E,AB=36cm,BC=24cm,S△ABC=144cm2,则DE的长是 .
12.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E,BC=5,DE=2,△BCE的面积等于 .
13.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上;⑤∠O=90°﹣∠A,其中结论正确的序号是 .
14.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC恰好平分∠ABF,AE=2BF.若CE=2,则AB= .
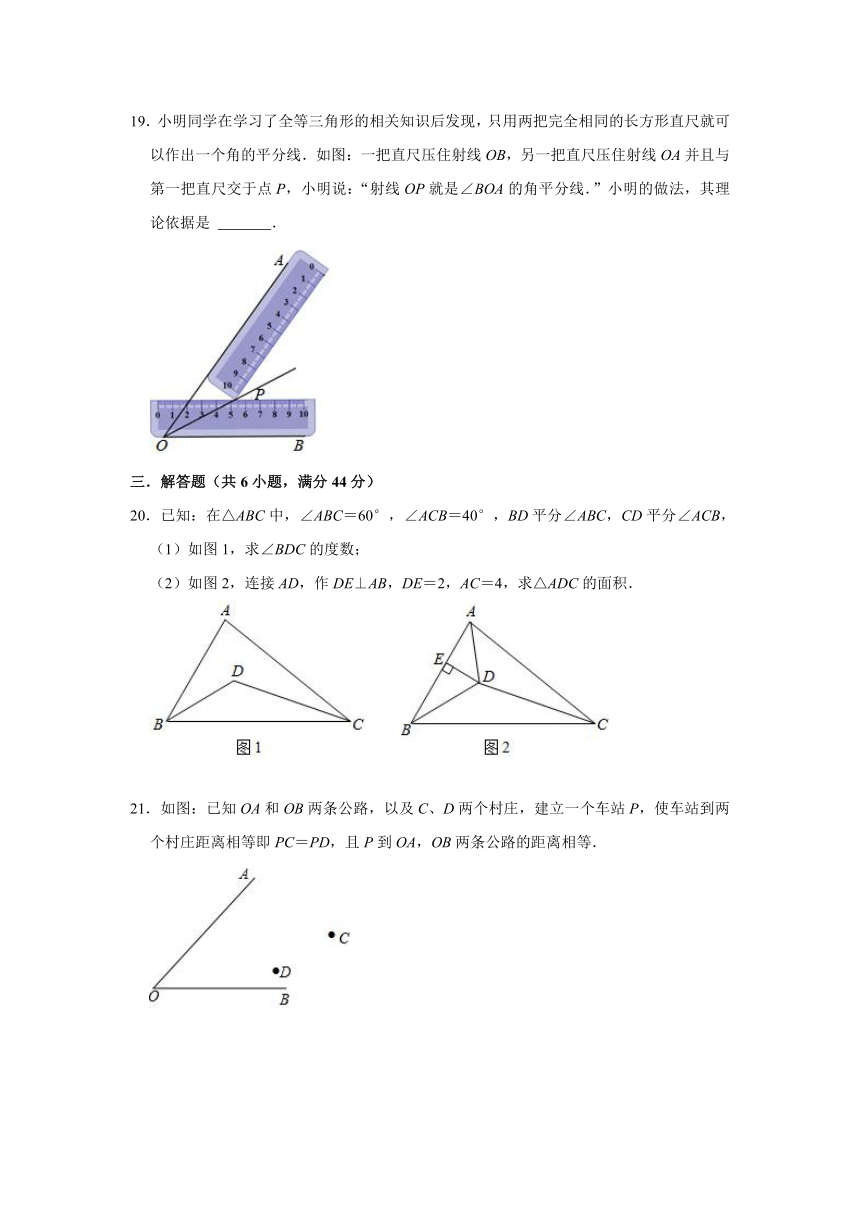
15.如图,△ABC外的一点P到三边所在直线的距离相等,若∠BAC=80°,则∠CPB= °.
16.将两块完全相同的三角尺在∠AOB的内部如图摆放,两块三角尺较短的直角边分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C,则射线OC即为∠AOB的平分线,理由是 .
17.如图△ABC中,∠ACB=90°,AB=10,AC=8,CB=6,I是三条角平分线的交点,ID⊥BC于D,则ID的长是 .
18.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3,AB=10,则△ABD的面积是 .
19.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 .
三.解答题(共6小题,满分44分)
20.已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
21.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
22.如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.
23.如图,点B,C分别在∠A的两边上,点D是∠A内一点,DE⊥AB,DF⊥AC,垂足分别为E,F,且AB=AC,DE=DF.求证:BD=CD.
24.已知:P为∠AOB内一个动点,M,N分别为OA,OB上的点,连接PM,PN,MN.
(1)如图1,若∠AOB=90°,OP=2,PM⊥OA,PN⊥OB,则MN的长为 .
(2)如图2,若∠AOB=120°,OP=2,若P在∠AOB的角平分线上,且满足PM=PN(OM<ON),求四边形OMPN的面积.
25.如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.
(1)证明:A,P,G三点共线;
(2)若∠G=68°,求∠P的度数.
参考答案
一.选择题(共9小题,满分36分)
1.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×10 DE=15,
解得:DE=3,
∴CD=3.
故选:B.
2.解:∵BD是∠ABC的平分线,DE⊥AB,∠C=90°,
∴DC=DE=4,
∵AC=10,
∴AD=AC﹣CD=10﹣4=6.
故选:C.
3.解:如图所示,过点D作DE⊥AB于E,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DC=DE,
∵S△ACD=6,
∴×AC×CD=6,即×6×CD=6,
解得CD=2,
∴DE=2,
即点D到AB的距离为2,
故选:B.
4.解:∵∠AOB=150°,PC∥OB交OA于点C,
∴∠PCO=30°,
过P作PE⊥OA于E,
∵PD⊥OB,OP平分∠AOB
∴PE=PD=3,∴∠AOP=∠POD=75°,
∴∠CPD=75°,
∴OC=PC=6,
故选:D.
5.解:满足条件的点有一个,
三角形内部:三个内角平分线交点一个.
三角形外部,外角的角平分线三个(不合题意).
故选:A.
6.解:∵CG⊥AB,
∴∠CGA=90°,
∴∠CAB+∠ACG=90°,
∵∠C=90°,
∴∠CAB+∠B=90°,
∴∠B=∠ACG,故①正确;
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵∠C=90°,∠CGA=90°,
∴∠CDE=90°﹣∠CAD,∠AEG=90°﹣∠BAD,
∴∠AEG=∠CDE,
∴∠CED=∠CDE,故③正确;
∴CE=CD,
∵AD平分∠BAC,∠C=90°,DF⊥AB,
∴CD=DF,
∴CE=DF,故②正确;
如图,过点E作EH⊥AC于点H,则EH=EG,
∴S△AEC==,
∵S△AEG=,
∴S△AEC:S△AEG=AC:AG,故④正确;
∴正确的个数是4个,
故选:A.
7.解:过点P作PE⊥OA于E,
∵OC平分∠AOB,PD⊥OB,PE⊥OA,
∴d=PE=PD=3cm,
故选:B.
8.解:①角的内部任意一点到角的两边的距离相等,是假命题;
②在角的内部到角的两边距离相等的点在这个角的平分线上,原命题是假命题;
③角的平分线上任意一点到角的两边的距离相等,是真命题;
④在△ABC中的∠BAC的平分线上任意一点到三角形三边的距离相等,是假命题;
故选:A.
9.解:∵AD是角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵AB=8,BC=9,AC=6,
∴S△ABD:S△ACD==AB:AC=8:6=4:3.
故选:A.
二.填空题(共10小题,满分40分)
10.解:
∵点O到△ABC三边的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣2(∠OBC+∠OCB)=180°﹣2×(180°﹣∠BOC)=180°﹣2×(180°﹣126°)=72°,
故答案为:72°.
11.解:如图,过D作DF⊥BC于F,
∵BD是∠ABC的平分线,DE⊥AB于点E,
∴DE=DF,
而S△ABC=S△ABD+S△CBD=DE AB+DF BC,
∴144=DE×36+DF×24,
∴144=18DE+12DF,
而DE=DF,
∴DE=4.8cm.
故填:4.8cm.
12.解:作EF⊥BC交BC于点F,
∵CD是AB边上的高,
∴CD⊥BA,
∵BE平分∠ABC,
∴DE=EF,
∵DE=2,
∴EF=2,
∵BC=5,
∴S△BCE===5,
故答案为:5.
13.解:如图,过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,
∵点O是△ABC的两外角平分线的交点,
∴OE=OG,OF=OG,
∴OE=OF=OG,
∴点O在∠A的平分线上,故②③④正确,
只有点F是BC的中点时,BO=CO,故①错误,
∵∠EBC=∠A+∠ACB,∠GCB=∠A+∠ABC,
∴∠EBC+∠GCB=2∠A+∠ABC+∠ACB=180°+∠A,
∵点O是△ABC的两外角平分线的交点,
∴∠CBO=∠EBC,∠BCO=∠BCG,
∴∠BOC=180°﹣∠CBO﹣∠BCO=90°﹣∠A,故⑤正确;
故答案为:②③④⑤.
14.解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD平分∠BAC,
∴DC=BD,
在△CDE与△DBF中,
,
∴△CDE≌△DBF(ASA)
∴DE=DF,CE=BF=2,
∵AE=2BF,
∴AC=3BF,
∴AB=3BF=6,
故答案为:6.
15.解:过P作PE⊥BA于E,PF⊥AC于F,PG⊥BC于G,
∵△ABC外的一点P到三边所在直线的距离相等,
∴PE=PF=PG,
∴BP平分∠ABC,PC平分∠ACD,
在△ABC中,∠ACD=∠BAC+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC,
∵PB、PC分别是∠ABC和∠ACD的平分线,
∴∠PCD=∠ACD,∠PBC=∠ABC,
∴∠BPC=∠PCD﹣∠PBC=∠ACD﹣ABC=(∠ACD﹣∠ABC)=∠BAC,
∵∠BAC=80°,
∴∠BPC=40°,
故答案为:40.
16.解:∵将两块完全相同的三角尺在∠AOB的内部如图摆放,
∴CE=CF,∠CEO=∠CFO=90°,
即CE⊥OA,CF⊥OB,
∴射线OC为∠AOB的平分线(角的内部到角的两边距离相等的点在角的平分线上),
故答案为:角的内部到角的两边距离相等的点在角的平分线上.
17.解:过I作IE⊥AC于E,IF⊥AB于F,连接IA,IC,IB,
∵I是三条角平分线的交点,ID⊥BC,
∴IE=ID=IF,
设IE=ID=IF=R,
∵△ABC中,∠ACB=90°,AC=8,CB=6,
∴△ABC的面积S=×AC×BC==24,
∴S△ACI+S△BCI+S△ABI=24,
∴AC×IE++IF=24,
∴+6×R+R=24,
解得:R=2,
即ID=2,
故答案为:2.
18.解:如图,作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=3,
∴△ABD的面积=×AB×DE=×10×3=15,
故答案为:15.
19.解:如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,
∵两把完全相同的长方形直尺,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故答案为:在角的内部,到角两边距离相等的点在角的平分线上.
三.解答题(共6小题,满分44分)
20.解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DF AC=×2×4=4.
21.解:如图,点P为所作.
22.证明:
过P作PE⊥BM于E,PF⊥AC于F,PG⊥BN于G,
∵P为∠ABC和∠MAC的平分线的交点,
∴PE=PF,PE=PG,
∴PF=PG,
∴点P在∠ACN的平分线上.
23.证明:连接AD,
∵DE⊥AB,DF⊥AC,DE=DF,
∴∠BAD=∠CAD,
在△ABD和△ACD中
,
∴△ABD≌△ACD,(SAS),
∴BD=CD.
24.解:(1)∵PM⊥OA,PN⊥OB,
∴∠OMP=∠MON=∠PNO=90°,
∴四边形PNOM是矩形,
∴MN=OP=2,
故答案为:2;
(2)过P作PG⊥OA,PH⊥OB,
∵P在∠AOB的角平分线上,
∴PG=PH,
在Rt△PGM与Rt△PHN中,,
∴Rt△PGM≌Rt△PHN,
∵∠AOB=120°,
∴∠POA=∠POB=60°,
∴OG=OH=1,PG=PH=,
∴四边形OMPN的面积=四边形PGOH的面积=2△OPG的面积=2××=.
25.解:(1)过G作GT⊥AN于T,GQ⊥AM于Q,PR⊥EF于R,
∵EG、FG分别是∠MEF,∠NFE的平分线,
∴GT=GR=GQ,
∴G在∠NAM的角平分线上,
同理点P在∠NAN的角平分线上,
∴A,P,G三点共线;
(2)∵EQ、FQ分别是∠MEF和∠NFE的平分线,
∴∠QFE=∠NFE,∠QEF=∠MEF,
∴∠Q=180°﹣∠NFE﹣∠MEF
=180°﹣(∠NFE+∠MEF)
=180°﹣(360°﹣∠AFE﹣∠AEF)
=180°﹣(180°+∠A)
=90°﹣∠A=68°,
同理,∠P=90°﹣∠A=68°.
一.选择题(共9小题,满分36分)
1.如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.2 B.3 C.4 D.5
2.如图,在Rt△ABC中,∠C=90°,BD是∠ABC的平分线,DE⊥AB于点E.若AC=10,DE=4,则AD的长为( )
A.2 B.4 C.6 D.8
3.如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若S△ACD=6,AC=6,则点D到AB的距离为( )
A.1 B.2 C.3 D.4
4.如图,∠AOB=150°,OP平分∠AOB,PD⊥OB于点D,PC∥OB交OA于点C,若PD=3,则OC的长为( )
A.3 B.4 C.5 D.6
5.为了加快灾后重建的步伐,我市某镇要在三条公路围成的一块平地上修建一个砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址( )
A.仅有一处 B.有四处 C.有七处 D.有无数处
6.如图,在Rt△ABC中,∠C=90°,∠A的平分线交BC于点D,过点C作CG⊥AB于点G,交AD于点E,过点D作DF⊥AB于点F.下列结论:
①∠B=∠ACG;②CE=DF;
③∠CED=∠CDE;
④S△AEC:S△AEG=AC:AG.
上述结论中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
7.如图,OC平分∠AOB,点P在OC上,且PD⊥OB,垂足为D,若PD=3cm,则P到OA的距离d满足( )
A.d<3cm B.d=3cm C.d>3cm D.无法确定
8.有下列四种说法:①角的内部任意一点到角的两边的距离相等;②到角的两边距离相等的点在这个角的平分线上;③角的平分线上任意一点到角的两边的距离相等;④在△ABC中的∠BAC的平分线上任意一点到三角形三边的距离相等,其中正确的有( )
A.1 B.2 C.3 D.4
9.如图,在△ABC中,AB=8,BC=9,AC=6,AD是角平分线,DE⊥AB,DF⊥AC,则S△ABD:S△ACD=( )
A.4:3 B.9:8 C.9:6 D.3:2
二.填空题(共10小题,满分40分)
10.如图,在△ABC中,O是△ABC内一点,且点O到△ABC三边的距离相等,∠BOC=126°,则∠A的度数为 .
11.如图所示,BD是∠ABC的平分线,DE⊥AB于点E,AB=36cm,BC=24cm,S△ABC=144cm2,则DE的长是 .
12.如图,在△ABC中,CD是AB边上的高,BE平分∠ABC交CD于点E,BC=5,DE=2,△BCE的面积等于 .
13.如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上;⑤∠O=90°﹣∠A,其中结论正确的序号是 .
14.如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,BC恰好平分∠ABF,AE=2BF.若CE=2,则AB= .
15.如图,△ABC外的一点P到三边所在直线的距离相等,若∠BAC=80°,则∠CPB= °.
16.将两块完全相同的三角尺在∠AOB的内部如图摆放,两块三角尺较短的直角边分别与∠AOB的两边重合,且含30°角的顶点恰好也重合于点C,则射线OC即为∠AOB的平分线,理由是 .
17.如图△ABC中,∠ACB=90°,AB=10,AC=8,CB=6,I是三条角平分线的交点,ID⊥BC于D,则ID的长是 .
18.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3,AB=10,则△ABD的面积是 .
19.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 .
三.解答题(共6小题,满分44分)
20.已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
21.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
22.如图,点P为∠ABC和∠MAC的平分线的交点.求证:点P在∠ACN的平分线上.
23.如图,点B,C分别在∠A的两边上,点D是∠A内一点,DE⊥AB,DF⊥AC,垂足分别为E,F,且AB=AC,DE=DF.求证:BD=CD.
24.已知:P为∠AOB内一个动点,M,N分别为OA,OB上的点,连接PM,PN,MN.
(1)如图1,若∠AOB=90°,OP=2,PM⊥OA,PN⊥OB,则MN的长为 .
(2)如图2,若∠AOB=120°,OP=2,若P在∠AOB的角平分线上,且满足PM=PN(OM<ON),求四边形OMPN的面积.
25.如图,EG、FG分别是∠MEF,∠NFE的平分线,交点是G,BP,CP分别是∠MBC和∠NCB的平分线,交点是P.
(1)证明:A,P,G三点共线;
(2)若∠G=68°,求∠P的度数.
参考答案
一.选择题(共9小题,满分36分)
1.解:如图,过点D作DE⊥AB于E,
∵∠C=90°,AD平分∠BAC,
∴DE=CD,
∴S△ABD=AB DE=×10 DE=15,
解得:DE=3,
∴CD=3.
故选:B.
2.解:∵BD是∠ABC的平分线,DE⊥AB,∠C=90°,
∴DC=DE=4,
∵AC=10,
∴AD=AC﹣CD=10﹣4=6.
故选:C.
3.解:如图所示,过点D作DE⊥AB于E,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DC=DE,
∵S△ACD=6,
∴×AC×CD=6,即×6×CD=6,
解得CD=2,
∴DE=2,
即点D到AB的距离为2,
故选:B.
4.解:∵∠AOB=150°,PC∥OB交OA于点C,
∴∠PCO=30°,
过P作PE⊥OA于E,
∵PD⊥OB,OP平分∠AOB
∴PE=PD=3,∴∠AOP=∠POD=75°,
∴∠CPD=75°,
∴OC=PC=6,
故选:D.
5.解:满足条件的点有一个,
三角形内部:三个内角平分线交点一个.
三角形外部,外角的角平分线三个(不合题意).
故选:A.
6.解:∵CG⊥AB,
∴∠CGA=90°,
∴∠CAB+∠ACG=90°,
∵∠C=90°,
∴∠CAB+∠B=90°,
∴∠B=∠ACG,故①正确;
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵∠C=90°,∠CGA=90°,
∴∠CDE=90°﹣∠CAD,∠AEG=90°﹣∠BAD,
∴∠AEG=∠CDE,
∴∠CED=∠CDE,故③正确;
∴CE=CD,
∵AD平分∠BAC,∠C=90°,DF⊥AB,
∴CD=DF,
∴CE=DF,故②正确;
如图,过点E作EH⊥AC于点H,则EH=EG,
∴S△AEC==,
∵S△AEG=,
∴S△AEC:S△AEG=AC:AG,故④正确;
∴正确的个数是4个,
故选:A.
7.解:过点P作PE⊥OA于E,
∵OC平分∠AOB,PD⊥OB,PE⊥OA,
∴d=PE=PD=3cm,
故选:B.
8.解:①角的内部任意一点到角的两边的距离相等,是假命题;
②在角的内部到角的两边距离相等的点在这个角的平分线上,原命题是假命题;
③角的平分线上任意一点到角的两边的距离相等,是真命题;
④在△ABC中的∠BAC的平分线上任意一点到三角形三边的距离相等,是假命题;
故选:A.
9.解:∵AD是角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵AB=8,BC=9,AC=6,
∴S△ABD:S△ACD==AB:AC=8:6=4:3.
故选:A.
二.填空题(共10小题,满分40分)
10.解:
∵点O到△ABC三边的距离相等,
∴BO平分∠ABC,CO平分∠ACB,
∴∠A=180°﹣(∠ABC+∠ACB)=180°﹣2(∠OBC+∠OCB)=180°﹣2×(180°﹣∠BOC)=180°﹣2×(180°﹣126°)=72°,
故答案为:72°.
11.解:如图,过D作DF⊥BC于F,
∵BD是∠ABC的平分线,DE⊥AB于点E,
∴DE=DF,
而S△ABC=S△ABD+S△CBD=DE AB+DF BC,
∴144=DE×36+DF×24,
∴144=18DE+12DF,
而DE=DF,
∴DE=4.8cm.
故填:4.8cm.
12.解:作EF⊥BC交BC于点F,
∵CD是AB边上的高,
∴CD⊥BA,
∵BE平分∠ABC,
∴DE=EF,
∵DE=2,
∴EF=2,
∵BC=5,
∴S△BCE===5,
故答案为:5.
13.解:如图,过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,
∵点O是△ABC的两外角平分线的交点,
∴OE=OG,OF=OG,
∴OE=OF=OG,
∴点O在∠A的平分线上,故②③④正确,
只有点F是BC的中点时,BO=CO,故①错误,
∵∠EBC=∠A+∠ACB,∠GCB=∠A+∠ABC,
∴∠EBC+∠GCB=2∠A+∠ABC+∠ACB=180°+∠A,
∵点O是△ABC的两外角平分线的交点,
∴∠CBO=∠EBC,∠BCO=∠BCG,
∴∠BOC=180°﹣∠CBO﹣∠BCO=90°﹣∠A,故⑤正确;
故答案为:②③④⑤.
14.解:∵BF∥AC,
∴∠C=∠CBF,
∵BC平分∠ABF,
∴∠ABC=∠CBF,
∴∠C=∠ABC,
∴AB=AC,
∵AD平分∠BAC,
∴DC=BD,
在△CDE与△DBF中,
,
∴△CDE≌△DBF(ASA)
∴DE=DF,CE=BF=2,
∵AE=2BF,
∴AC=3BF,
∴AB=3BF=6,
故答案为:6.
15.解:过P作PE⊥BA于E,PF⊥AC于F,PG⊥BC于G,
∵△ABC外的一点P到三边所在直线的距离相等,
∴PE=PF=PG,
∴BP平分∠ABC,PC平分∠ACD,
在△ABC中,∠ACD=∠BAC+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC,
∵PB、PC分别是∠ABC和∠ACD的平分线,
∴∠PCD=∠ACD,∠PBC=∠ABC,
∴∠BPC=∠PCD﹣∠PBC=∠ACD﹣ABC=(∠ACD﹣∠ABC)=∠BAC,
∵∠BAC=80°,
∴∠BPC=40°,
故答案为:40.
16.解:∵将两块完全相同的三角尺在∠AOB的内部如图摆放,
∴CE=CF,∠CEO=∠CFO=90°,
即CE⊥OA,CF⊥OB,
∴射线OC为∠AOB的平分线(角的内部到角的两边距离相等的点在角的平分线上),
故答案为:角的内部到角的两边距离相等的点在角的平分线上.
17.解:过I作IE⊥AC于E,IF⊥AB于F,连接IA,IC,IB,
∵I是三条角平分线的交点,ID⊥BC,
∴IE=ID=IF,
设IE=ID=IF=R,
∵△ABC中,∠ACB=90°,AC=8,CB=6,
∴△ABC的面积S=×AC×BC==24,
∴S△ACI+S△BCI+S△ABI=24,
∴AC×IE++IF=24,
∴+6×R+R=24,
解得:R=2,
即ID=2,
故答案为:2.
18.解:如图,作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=3,
∴△ABD的面积=×AB×DE=×10×3=15,
故答案为:15.
19.解:如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,
∵两把完全相同的长方形直尺,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故答案为:在角的内部,到角两边距离相等的点在角的平分线上.
三.解答题(共6小题,满分44分)
20.解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DF AC=×2×4=4.
21.解:如图,点P为所作.
22.证明:
过P作PE⊥BM于E,PF⊥AC于F,PG⊥BN于G,
∵P为∠ABC和∠MAC的平分线的交点,
∴PE=PF,PE=PG,
∴PF=PG,
∴点P在∠ACN的平分线上.
23.证明:连接AD,
∵DE⊥AB,DF⊥AC,DE=DF,
∴∠BAD=∠CAD,
在△ABD和△ACD中
,
∴△ABD≌△ACD,(SAS),
∴BD=CD.
24.解:(1)∵PM⊥OA,PN⊥OB,
∴∠OMP=∠MON=∠PNO=90°,
∴四边形PNOM是矩形,
∴MN=OP=2,
故答案为:2;
(2)过P作PG⊥OA,PH⊥OB,
∵P在∠AOB的角平分线上,
∴PG=PH,
在Rt△PGM与Rt△PHN中,,
∴Rt△PGM≌Rt△PHN,
∵∠AOB=120°,
∴∠POA=∠POB=60°,
∴OG=OH=1,PG=PH=,
∴四边形OMPN的面积=四边形PGOH的面积=2△OPG的面积=2××=.
25.解:(1)过G作GT⊥AN于T,GQ⊥AM于Q,PR⊥EF于R,
∵EG、FG分别是∠MEF,∠NFE的平分线,
∴GT=GR=GQ,
∴G在∠NAM的角平分线上,
同理点P在∠NAN的角平分线上,
∴A,P,G三点共线;
(2)∵EQ、FQ分别是∠MEF和∠NFE的平分线,
∴∠QFE=∠NFE,∠QEF=∠MEF,
∴∠Q=180°﹣∠NFE﹣∠MEF
=180°﹣(∠NFE+∠MEF)
=180°﹣(360°﹣∠AFE﹣∠AEF)
=180°﹣(180°+∠A)
=90°﹣∠A=68°,
同理,∠P=90°﹣∠A=68°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
