2021-2022学年北师大版八年级数学下册1.3线段的垂直平分线 同步自主达标测评(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学下册1.3线段的垂直平分线 同步自主达标测评(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 159.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 07:44:36 | ||
图片预览



文档简介
2021-2022学年北师大版八年级数学下册《1-3线段的垂直平分线》
同步自主达标测评(附答案)
一.选择题(共8小题,满分40分)
1.到△ABC的三个顶点距离相等的点是( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高线的交点 D.三条边的垂直平分线的交点
2.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.26cm B.21cm C.28cm D.31cm
3.《中共中央国务院关于促进农民增加收入若干政策的意见》中提出“进一步精简乡镇机构和财政供养人员,积极稳妥地调整乡镇建制,有条件的可实行并村”.《中共中央国务院关于积极发展现代农业扎实推进社会主义新农村建设的若干意见》中明确提出“治理农村人居环境,搞好村庄治理规划和试点,节约农村建设用地”.以上两个政策出台后,山东陆陆续续开展了村庄合并某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )
A.三条边的垂直平分线的交点处 B.三个角的平分线的交点处
C.三角形三条高线的交点处 D.三角形三条中线的交点处
4.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
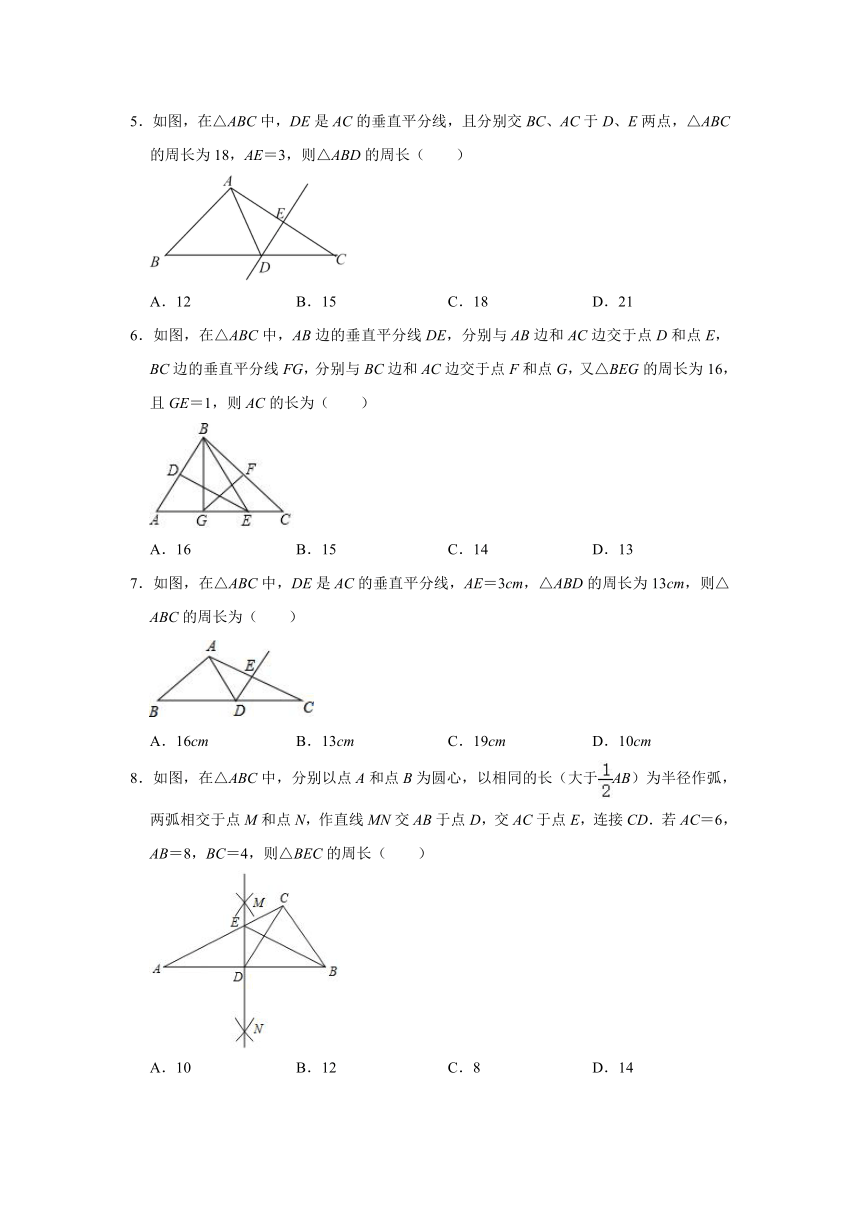
5.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,△ABC的周长为18,AE=3,则△ABD的周长( )
A.12 B.15 C.18 D.21
6.如图,在△ABC中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又△BEG的周长为16,且GE=1,则AC的长为( )
A.16 B.15 C.14 D.13
7.如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A.16cm B.13cm C.19cm D.10cm
8.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.若AC=6,AB=8,BC=4,则△BEC的周长( )
A.10 B.12 C.8 D.14
二.填空题(共7小题,满分35分)
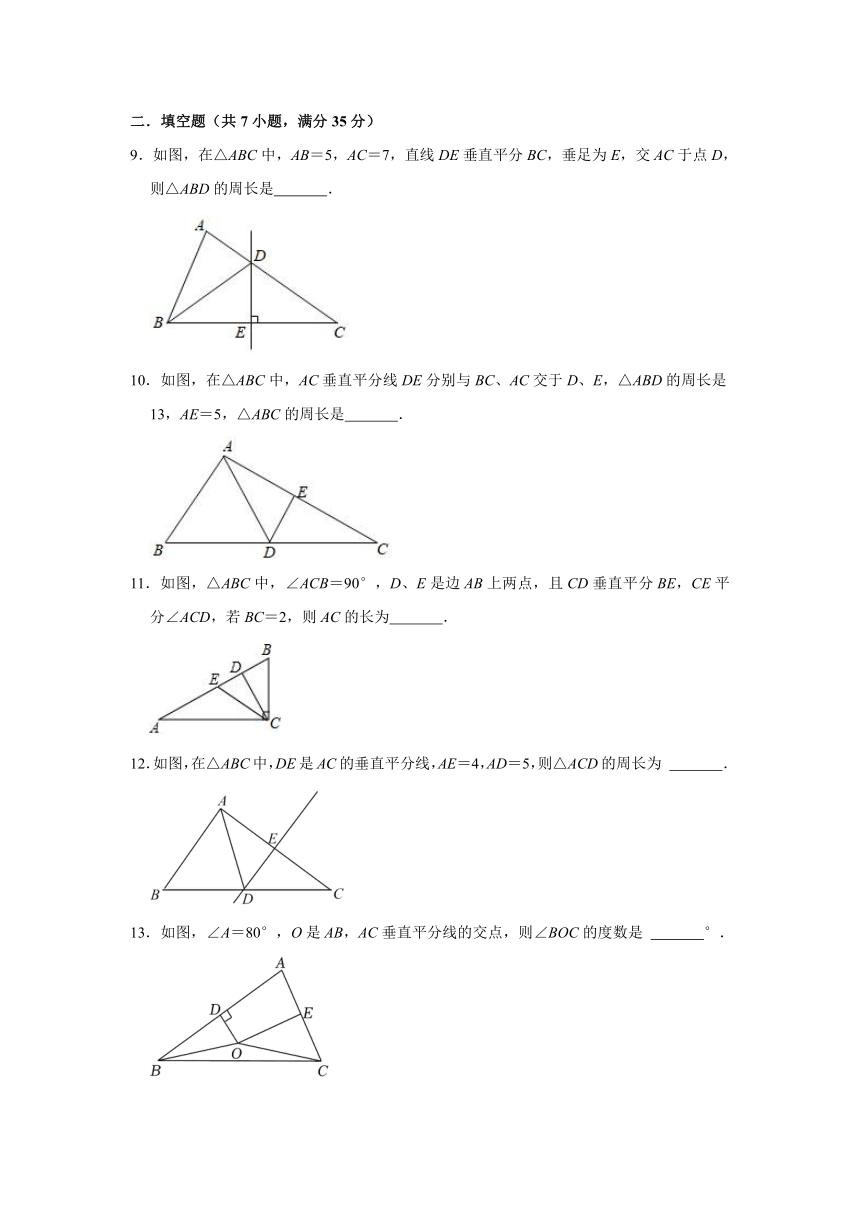
9.如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是 .
10.如图,在△ABC中,AC垂直平分线DE分别与BC、AC交于D、E,△ABD的周长是13,AE=5,△ABC的周长是 .
11.如图,△ABC中,∠ACB=90°,D、E是边AB上两点,且CD垂直平分BE,CE平分∠ACD,若BC=2,则AC的长为 .
12.如图,在△ABC中,DE是AC的垂直平分线,AE=4,AD=5,则△ACD的周长为 .
13.如图,∠A=80°,O是AB,AC垂直平分线的交点,则∠BOC的度数是 °.
14.如图,在△ABC中,DE是AB的垂直平分线,且分别交AB,AC于点D,E,若∠A=45°,∠C=65°,则∠EBC的度数为 .
15.如图,在△ABC中,∠BAC=126°,MP和NQ分别是AB和AC的垂直平分线,则∠PAQ的度数 .
三.解答题(共7小题,满分45分)
16.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=20°,求∠C的度数.
17.如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD=∠E.
18.如图所示,已知AB=AC=20cm,DE垂直平分AB,垂足为E,DE交AC于点D,若△EBC的周长为35cm,求BC的长.
19.如图,在△ABC中,∠BAC=90°,∠C=65°,AD⊥BC,EF是边AB的垂直平分线,交BC于点E,交AB于点F,求∠DAE的度数.
20.如图,△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G,连接AE,AG.
(1)若△AEG的周长为10,求线段BC的长;
(2)若∠BAC=104°,求∠EAG的度数.
21.如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.
22.如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作BC的平行线AF交CD于F,延长AB、DC交于点E.
求证:(1)AC平分∠EAF;
(2)∠FAD=∠E.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,
∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选:D.
2.解:∵DE是AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长为16,
∴AB+BD+AD=AB+BD+DC=AB+BC=16,
∴△ABC的周长=AB+BC+AC=16+10=26(cm),
故选:A.
3.解:∵电动车充电桩到三个出口的距离都相等,
∴充电桩应该在三条边的垂直平分线的交点处,
故选:A.
4.解:∵DE是AB的垂直平分线,
∴EA=EB,
由题意得,BC+CE+BE=18,
则BC+CE+AE=18,即BC+AC=18,又BC=8,
∴AC=10,
故选:B.
5.解:∵DE是AC的垂直平分线,AE=3,
∴DA=DC,AC=2AE=6,
∵△ABC的周长是18,
∴AB+BC+AC=18,
∴AB+BC=12,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=12,
故选:A.
6.解:∵DE是AB边的垂直平分线,
∴EB=EA,
∵FG是BC边的垂直平分线,
∴GB=GC,
∵△BEG的周长为16,
∴GB+GE+EB=16,
∴AE+GE+GC=16,
∴AC+GE+GE=16,
∵GE=1,
∴AC=16﹣2=14,
故选:C.
7.解:∵DE是AC的垂直平分线,AE=3cm,
∴AC=2AE=6cm,AD=DC,
∵△ABD的周长为13cm,
∴AB+BD+AD=13cm,
∴AB+BD+DC=AB+BC=13cm,
∴△ABC的周长为AB+BC+AC=13cm+6cm=19cm,
故选:C.
8.解:从作法可知:DE是AB的垂直平分线,
∴EA=EB,
∴△BCE的周长=EB+EC+BC=AC+BC=6+4=10,
故选:A.
二.填空题(共7小题,满分35分)
9.解:∵DE垂直平分BC,
∴DB=DC.
∴C△ABD=AB+AD+BD=AB+AD+DC=AB+AC=12.
∴△ABD的周长是12.
故答案为:12.
10.解:∵DE是线段AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长是13,
∴AB+BD+DA=13,
∴AB+BD+DC=AB+BC=13,
∴△ABC的周长=AB+BC+AC=23,
故答案为:23.
11.解:∵CD垂直平分BE,
∴CE=CB,∠BDC=90°,
∴CD平分∠BCE,即∠BCD=∠ECD,
∵CE平分∠ACD,
∴∠ECD=∠ACE,
而∠ACB=90°,
∴∠BCD=∠ACB=30°,
∴∠B=60°,
∴∠A=30°,
∴AC=BC=2.
故答案为2.
12.解:∵DE是AC的垂直平分线,
∴AD=CD=5,AC=2AE=2×4=8,
∴△ADC的周长是:AD+CD+AC=18.
故答案为:18.
13.解:连接OA、OB,
∵∠A=80°,
∴∠ABC+∠ACB=100°,
∵O是AB,AC垂直平分线的交点,
∴OA=OB,OA=OC,
∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=80°,
∴∠OBC+∠OCB=100°﹣80°=20°,
∵OB=OC,
∴∠BCO=∠CBO=10°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=160°,
故答案为:160°.
14.解:∵A=45°,∠C=65°,
∴∠ABC=180°﹣45°﹣65°=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=50°,
∴∠EBC=∠ABC﹣∠EBA=70°﹣45°=25°,
故答案为:25°.
15.解:∵∠BAC=126°,
∴∠ABP+∠ACQ=180°﹣126°=54°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=54°,
∴∠PAQ=126°﹣54°=72°.
故答案为:72°.
三.解答题(共7小题,满分45分)
16.解:∵ED是AC的垂直平分线,
∴EA=EC,
∴∠C=∠EAC,
∴∠CAB=∠EAC+20°=∠C+20°,
∵∠C+∠CAB=90°,
∴2∠C+20°=90°,
∴∠C=35°;
17.证明:(1)∵点C是AB的垂直平分线上的点,
∴CB=CA,
∴∠CBA=∠CAB,
∵AF∥BC交DE于点F,
∴∠BAF=∠CBA,
∴∠BAF=∠CAB.
即 AB是∠CAF的角平分线.
(2)∵点D是AB的垂直平分线上的点,
∴DB=DA,
∴∠DBA=∠DAB,
∵∠DBA=∠E+∠CAB,∠DAB=∠FAD+∠BAF,∠CAB=∠BAF,
∴∠E=∠FAD.
18.解:∵DE垂直平分AB,
∴EA=EB,
∵AC=20cm,
∴BE+EC=AE+EC=AC=20cm,
∵△EBC的周长为35cm,即BE+EC+BC=35cm,
∴BC=15cm.
19.解:∵∠BAC=90°,∠C=65°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣90°﹣65°=25°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=25°,
∵EF是边AB的垂直平分线,
∴EA=EB,
∴∠BAE=∠B=25°,
∴∠DAE=90°﹣25°﹣25°=40°.
20.解:(1)∵DE垂直平分AB,GF垂直平分AC,
∴EA=EB,GA=GC,
∵△AEG的周长为10,
∴AE+EG+AG=10,
∴BC=BE+EG+GC=AE+EG+GC=10;
(2)∵∠BAC=104°,
∴∠B+∠C=180°﹣104°=76°,
∵EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=76°,
∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=104°﹣76°=28°.
21.(1)证明:连接AC,
∵M是CD的中点,AM⊥CD,
∴AM是线段CD的垂直平分线,
∴AC=AD,又AM⊥CD,
∴∠3=∠4,
同理,∠1=∠2,
∴∠2+∠3=∠BAD,即∠BAD=2∠MAN;
(2)∵AM⊥CD,AN⊥BC.∠MAN=70°,
∴∠BCD=360°﹣90°﹣90°﹣70°=110°,
∴∠BDC=180°﹣∠DBC﹣∠BCD=30°,
∠BAD=2∠MAN=140°,
∵AB=AC,AD=AC,
∴AB=AD,
∴∠ADB=∠ABD=20°,
∴∠ADC=∠ADB+∠BDC=50°.
22.证明:(1)∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,即AC平分∠EAF;
(2)∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E.
同步自主达标测评(附答案)
一.选择题(共8小题,满分40分)
1.到△ABC的三个顶点距离相等的点是( )
A.三条中线的交点 B.三条角平分线的交点
C.三条高线的交点 D.三条边的垂直平分线的交点
2.如图,△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为16cm,则△ABC的周长为( )
A.26cm B.21cm C.28cm D.31cm
3.《中共中央国务院关于促进农民增加收入若干政策的意见》中提出“进一步精简乡镇机构和财政供养人员,积极稳妥地调整乡镇建制,有条件的可实行并村”.《中共中央国务院关于积极发展现代农业扎实推进社会主义新农村建设的若干意见》中明确提出“治理农村人居环境,搞好村庄治理规划和试点,节约农村建设用地”.以上两个政策出台后,山东陆陆续续开展了村庄合并某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在( )
A.三条边的垂直平分线的交点处 B.三个角的平分线的交点处
C.三角形三条高线的交点处 D.三角形三条中线的交点处
4.如图,在△ABC中,BC=8,AB的垂直平分线分别交AB、AC于点D、E,△BCE的周长为18,则AC的长等于( )
A.12 B.10 C.8 D.6
5.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,△ABC的周长为18,AE=3,则△ABD的周长( )
A.12 B.15 C.18 D.21
6.如图,在△ABC中,AB边的垂直平分线DE,分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG,分别与BC边和AC边交于点F和点G,又△BEG的周长为16,且GE=1,则AC的长为( )
A.16 B.15 C.14 D.13
7.如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
A.16cm B.13cm C.19cm D.10cm
8.如图,在△ABC中,分别以点A和点B为圆心,以相同的长(大于AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交AC于点E,连接CD.若AC=6,AB=8,BC=4,则△BEC的周长( )
A.10 B.12 C.8 D.14
二.填空题(共7小题,满分35分)
9.如图,在△ABC中,AB=5,AC=7,直线DE垂直平分BC,垂足为E,交AC于点D,则△ABD的周长是 .
10.如图,在△ABC中,AC垂直平分线DE分别与BC、AC交于D、E,△ABD的周长是13,AE=5,△ABC的周长是 .
11.如图,△ABC中,∠ACB=90°,D、E是边AB上两点,且CD垂直平分BE,CE平分∠ACD,若BC=2,则AC的长为 .
12.如图,在△ABC中,DE是AC的垂直平分线,AE=4,AD=5,则△ACD的周长为 .
13.如图,∠A=80°,O是AB,AC垂直平分线的交点,则∠BOC的度数是 °.
14.如图,在△ABC中,DE是AB的垂直平分线,且分别交AB,AC于点D,E,若∠A=45°,∠C=65°,则∠EBC的度数为 .
15.如图,在△ABC中,∠BAC=126°,MP和NQ分别是AB和AC的垂直平分线,则∠PAQ的度数 .
三.解答题(共7小题,满分45分)
16.如图,在Rt△ABC中,∠B=90°,ED是AC的垂直平分线,交AC于点D,交BC于点E.已知∠BAE=20°,求∠C的度数.
17.如图,C,D是AB的垂直平分线上两点,延长AC,DB交于点E,AF∥BC交DE于点F.
求证:(1)AB是∠CAF的角平分线;
(2)∠FAD=∠E.
18.如图所示,已知AB=AC=20cm,DE垂直平分AB,垂足为E,DE交AC于点D,若△EBC的周长为35cm,求BC的长.
19.如图,在△ABC中,∠BAC=90°,∠C=65°,AD⊥BC,EF是边AB的垂直平分线,交BC于点E,交AB于点F,求∠DAE的度数.
20.如图,△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G,连接AE,AG.
(1)若△AEG的周长为10,求线段BC的长;
(2)若∠BAC=104°,求∠EAG的度数.
21.如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.
22.如图,在四边形ABCD中,BD所在的直线垂直平分线段AC,过点A作BC的平行线AF交CD于F,延长AB、DC交于点E.
求证:(1)AC平分∠EAF;
(2)∠FAD=∠E.
参考答案
一.选择题(共8小题,满分40分)
1.解:∵到三角形的一边的两端点距离相等的点在这边的垂直平分线上,
∴到三角形三个顶点的距离都相等的点是这个三角形的三条边的垂直平分线的交点,
故选:D.
2.解:∵DE是AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长为16,
∴AB+BD+AD=AB+BD+DC=AB+BC=16,
∴△ABC的周长=AB+BC+AC=16+10=26(cm),
故选:A.
3.解:∵电动车充电桩到三个出口的距离都相等,
∴充电桩应该在三条边的垂直平分线的交点处,
故选:A.
4.解:∵DE是AB的垂直平分线,
∴EA=EB,
由题意得,BC+CE+BE=18,
则BC+CE+AE=18,即BC+AC=18,又BC=8,
∴AC=10,
故选:B.
5.解:∵DE是AC的垂直平分线,AE=3,
∴DA=DC,AC=2AE=6,
∵△ABC的周长是18,
∴AB+BC+AC=18,
∴AB+BC=12,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC=12,
故选:A.
6.解:∵DE是AB边的垂直平分线,
∴EB=EA,
∵FG是BC边的垂直平分线,
∴GB=GC,
∵△BEG的周长为16,
∴GB+GE+EB=16,
∴AE+GE+GC=16,
∴AC+GE+GE=16,
∵GE=1,
∴AC=16﹣2=14,
故选:C.
7.解:∵DE是AC的垂直平分线,AE=3cm,
∴AC=2AE=6cm,AD=DC,
∵△ABD的周长为13cm,
∴AB+BD+AD=13cm,
∴AB+BD+DC=AB+BC=13cm,
∴△ABC的周长为AB+BC+AC=13cm+6cm=19cm,
故选:C.
8.解:从作法可知:DE是AB的垂直平分线,
∴EA=EB,
∴△BCE的周长=EB+EC+BC=AC+BC=6+4=10,
故选:A.
二.填空题(共7小题,满分35分)
9.解:∵DE垂直平分BC,
∴DB=DC.
∴C△ABD=AB+AD+BD=AB+AD+DC=AB+AC=12.
∴△ABD的周长是12.
故答案为:12.
10.解:∵DE是线段AC的垂直平分线,
∴DA=DC,AC=2AE=10,
∵△ABD的周长是13,
∴AB+BD+DA=13,
∴AB+BD+DC=AB+BC=13,
∴△ABC的周长=AB+BC+AC=23,
故答案为:23.
11.解:∵CD垂直平分BE,
∴CE=CB,∠BDC=90°,
∴CD平分∠BCE,即∠BCD=∠ECD,
∵CE平分∠ACD,
∴∠ECD=∠ACE,
而∠ACB=90°,
∴∠BCD=∠ACB=30°,
∴∠B=60°,
∴∠A=30°,
∴AC=BC=2.
故答案为2.
12.解:∵DE是AC的垂直平分线,
∴AD=CD=5,AC=2AE=2×4=8,
∴△ADC的周长是:AD+CD+AC=18.
故答案为:18.
13.解:连接OA、OB,
∵∠A=80°,
∴∠ABC+∠ACB=100°,
∵O是AB,AC垂直平分线的交点,
∴OA=OB,OA=OC,
∴∠OAB=∠OBA,∠OCA=∠OAC,OB=OC,
∴∠OBA+∠OCA=80°,
∴∠OBC+∠OCB=100°﹣80°=20°,
∵OB=OC,
∴∠BCO=∠CBO=10°,
∴∠BOC=180°﹣∠OBC﹣∠OCB=160°,
故答案为:160°.
14.解:∵A=45°,∠C=65°,
∴∠ABC=180°﹣45°﹣65°=70°,
∵DE是AB的垂直平分线,
∴EA=EB,
∴∠EBA=∠A=50°,
∴∠EBC=∠ABC﹣∠EBA=70°﹣45°=25°,
故答案为:25°.
15.解:∵∠BAC=126°,
∴∠ABP+∠ACQ=180°﹣126°=54°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=54°,
∴∠PAQ=126°﹣54°=72°.
故答案为:72°.
三.解答题(共7小题,满分45分)
16.解:∵ED是AC的垂直平分线,
∴EA=EC,
∴∠C=∠EAC,
∴∠CAB=∠EAC+20°=∠C+20°,
∵∠C+∠CAB=90°,
∴2∠C+20°=90°,
∴∠C=35°;
17.证明:(1)∵点C是AB的垂直平分线上的点,
∴CB=CA,
∴∠CBA=∠CAB,
∵AF∥BC交DE于点F,
∴∠BAF=∠CBA,
∴∠BAF=∠CAB.
即 AB是∠CAF的角平分线.
(2)∵点D是AB的垂直平分线上的点,
∴DB=DA,
∴∠DBA=∠DAB,
∵∠DBA=∠E+∠CAB,∠DAB=∠FAD+∠BAF,∠CAB=∠BAF,
∴∠E=∠FAD.
18.解:∵DE垂直平分AB,
∴EA=EB,
∵AC=20cm,
∴BE+EC=AE+EC=AC=20cm,
∵△EBC的周长为35cm,即BE+EC+BC=35cm,
∴BC=15cm.
19.解:∵∠BAC=90°,∠C=65°,
∴∠B=180°﹣∠BAC﹣∠C=180°﹣90°﹣65°=25°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=90°﹣∠C=25°,
∵EF是边AB的垂直平分线,
∴EA=EB,
∴∠BAE=∠B=25°,
∴∠DAE=90°﹣25°﹣25°=40°.
20.解:(1)∵DE垂直平分AB,GF垂直平分AC,
∴EA=EB,GA=GC,
∵△AEG的周长为10,
∴AE+EG+AG=10,
∴BC=BE+EG+GC=AE+EG+GC=10;
(2)∵∠BAC=104°,
∴∠B+∠C=180°﹣104°=76°,
∵EA=EB,GA=GC,
∴∠EAB=∠B,∠GAC=∠C,
∴∠EAB+∠GAC=∠B+∠C=76°,
∴∠EAG=∠BAC﹣(∠EAB+∠GAC)=104°﹣76°=28°.
21.(1)证明:连接AC,
∵M是CD的中点,AM⊥CD,
∴AM是线段CD的垂直平分线,
∴AC=AD,又AM⊥CD,
∴∠3=∠4,
同理,∠1=∠2,
∴∠2+∠3=∠BAD,即∠BAD=2∠MAN;
(2)∵AM⊥CD,AN⊥BC.∠MAN=70°,
∴∠BCD=360°﹣90°﹣90°﹣70°=110°,
∴∠BDC=180°﹣∠DBC﹣∠BCD=30°,
∠BAD=2∠MAN=140°,
∵AB=AC,AD=AC,
∴AB=AD,
∴∠ADB=∠ABD=20°,
∴∠ADC=∠ADB+∠BDC=50°.
22.证明:(1)∵BD所在的直线垂直平分线段AC,
∴BA=BC,
∴∠BAC=∠BCA,
∵BC∥AF,
∴∠CAF=∠BCA,
∴∠CAF=∠BAC,即AC平分∠EAF;
(2)∵BD所在的直线垂直平分线段AC,
∴DA=DC,
∴∠DAC=∠DCA,
∵∠DCA是△ACE的一个外角,
∴∠DCA=∠E+∠EAC,
∴∠E+∠EAC=∠FAD+∠CAF,
∵∠CAF=∠EAC,
∴∠FAD=∠E.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
