人教版七年级数学 下册 第八章 8.4 三元一次方程组的解法 同步练习题(含答案)
文档属性
| 名称 | 人教版七年级数学 下册 第八章 8.4 三元一次方程组的解法 同步练习题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 119.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-20 20:07:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第八章 二元一次方程组
8.4 三元一次方程组的解法
一、选择题
1.在方程中,若,则的值为( )
A.4 B.3 C.2 D.1
2.观察方程组的系数特点,若要使求解简便,消元的方法应选取( )
A.先消去x B.先消去y C.先消去z D.以上说法都不对
3.三元一次方程组的解是( )
A. B.
C. D.
4.若方程组 的解x与y相等,则a的值等于( )
A.4 B.10 C.11 D.12
5.若,,则的值为( )
A.5 B.4 C.3 D.2
填空题
6.若则x+y+z=__________________.
7.若x+y+z≠0且,则k=_________.
8.代数式ax2+bx+c,当x=1时值为0,当x=2时值为3,当x=-3时值为28,则这个代数式是_________.
9.一个三位数,个位、百位上的数字的和等于十位上的数字,百位上的数字的7倍比个位、十位上的数字的和大2,个位、十位、百位上的数字的和是14,则这个三位数是__________.
10.确保信息安全,信息需加密传输,发送方由明文密文(加密),接收方由密文明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为___________.
三、解答题
11.(1) (2) (3)
12.若|x+2y-5|+(2y+3z-13)2+(3z+x-10)2=0,试求x,y,z的值.
13.甲、乙、丙三个班的学生共植树66棵,甲班植树的棵数是乙班植树棵数的2倍,丙班与乙班植树棵数比为2∶3,求三个班各植树多少棵
14.若,求x、y、z的值。
15.现有一种饮料,它有大、中、小3种包装,其中1个中瓶比2个小瓶便宜2角,1个大瓶比1个中瓶加1个小瓶贵4角,大、中、小各买1瓶,需9元6角,三种包装的饮料每瓶各多少元?
16.三个数的和是51,第二个数去除第一个数时商2余5,第三个数去除第二个数时商3余2,求这三个数.
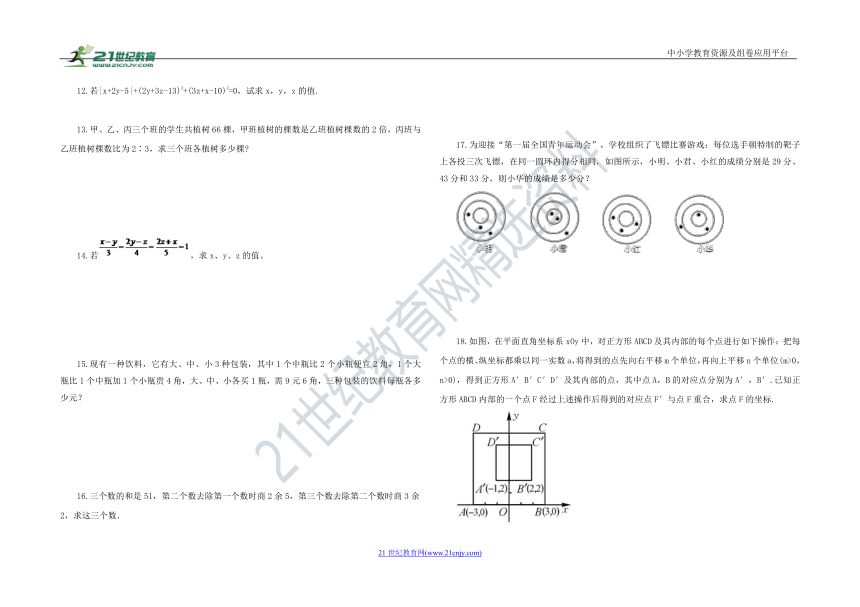
17.为迎接“第一届全国青年运动会”,学校组织了飞镖比赛游戏:每位选手朝特制的靶子上各投三次飞镖,在同一圆环内得分相同.如图所示,小明、小君、小红的成绩分别是29分、43分和33分,则小华的成绩是多少分?
18.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
参考答案:
一、1.A 2.B 3.D 4.C 5.A
二、6.3
7.3
8.2x2-3x+1.
9.275
10.6,4,1,7
三、11.(1) (2)
(3)
12.解:∵|x+2y-5|+(2y+3z-13)2+(3z+x-10)2=0,,∴解得∴x=1,y=2,z=3.
13.设甲、乙、丙3个班分别植树x、y、z棵,
则解得
14.解:∵,∴由②×2+③得x+4y=13④,由④-①得5y=10,∴y=2⑤,将⑤分别代入①和②得x=5,z=0,∴即x=5,y=2,z=0.
15.解:设大、中、小3种包装的饮料每瓶各x元、y元、z元.
由题意得解得
答:大、中、小3种包装的饮料每瓶各5元、3元、1.6元.
16.设三个数分别为x,y,z,
则解得
17.解:设小、中、大圆环的得分分别为x分、y分、z分.
由题意得解得则x+y+z=18+11+7=36(分).
答:小华的成绩是36分.
18.解:由题意,A(-3,0),B(3,0)的对应点分别为A’(-1,2),B’(2,2),
∴-3a+m=-1,0+n=2,3a+m=2,,0+n=2,解得a=,m=,n=2.
设F的坐标为(x,y).∵对应点F′与点F重合,∴x+=x,y+2=y,解得x=1,y=4,则F的坐标为(1,4).
21世纪教育网(www.21cnjy.com)
第八章 二元一次方程组
8.4 三元一次方程组的解法
一、选择题
1.在方程中,若,则的值为( )
A.4 B.3 C.2 D.1
2.观察方程组的系数特点,若要使求解简便,消元的方法应选取( )
A.先消去x B.先消去y C.先消去z D.以上说法都不对
3.三元一次方程组的解是( )
A. B.
C. D.
4.若方程组 的解x与y相等,则a的值等于( )
A.4 B.10 C.11 D.12
5.若,,则的值为( )
A.5 B.4 C.3 D.2
填空题
6.若则x+y+z=__________________.
7.若x+y+z≠0且,则k=_________.
8.代数式ax2+bx+c,当x=1时值为0,当x=2时值为3,当x=-3时值为28,则这个代数式是_________.
9.一个三位数,个位、百位上的数字的和等于十位上的数字,百位上的数字的7倍比个位、十位上的数字的和大2,个位、十位、百位上的数字的和是14,则这个三位数是__________.
10.确保信息安全,信息需加密传输,发送方由明文密文(加密),接收方由密文明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d.例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为___________.
三、解答题
11.(1) (2) (3)
12.若|x+2y-5|+(2y+3z-13)2+(3z+x-10)2=0,试求x,y,z的值.
13.甲、乙、丙三个班的学生共植树66棵,甲班植树的棵数是乙班植树棵数的2倍,丙班与乙班植树棵数比为2∶3,求三个班各植树多少棵
14.若,求x、y、z的值。
15.现有一种饮料,它有大、中、小3种包装,其中1个中瓶比2个小瓶便宜2角,1个大瓶比1个中瓶加1个小瓶贵4角,大、中、小各买1瓶,需9元6角,三种包装的饮料每瓶各多少元?
16.三个数的和是51,第二个数去除第一个数时商2余5,第三个数去除第二个数时商3余2,求这三个数.
17.为迎接“第一届全国青年运动会”,学校组织了飞镖比赛游戏:每位选手朝特制的靶子上各投三次飞镖,在同一圆环内得分相同.如图所示,小明、小君、小红的成绩分别是29分、43分和33分,则小华的成绩是多少分?
18.如图,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
参考答案:
一、1.A 2.B 3.D 4.C 5.A
二、6.3
7.3
8.2x2-3x+1.
9.275
10.6,4,1,7
三、11.(1) (2)
(3)
12.解:∵|x+2y-5|+(2y+3z-13)2+(3z+x-10)2=0,,∴解得∴x=1,y=2,z=3.
13.设甲、乙、丙3个班分别植树x、y、z棵,
则解得
14.解:∵,∴由②×2+③得x+4y=13④,由④-①得5y=10,∴y=2⑤,将⑤分别代入①和②得x=5,z=0,∴即x=5,y=2,z=0.
15.解:设大、中、小3种包装的饮料每瓶各x元、y元、z元.
由题意得解得
答:大、中、小3种包装的饮料每瓶各5元、3元、1.6元.
16.设三个数分别为x,y,z,
则解得
17.解:设小、中、大圆环的得分分别为x分、y分、z分.
由题意得解得则x+y+z=18+11+7=36(分).
答:小华的成绩是36分.
18.解:由题意,A(-3,0),B(3,0)的对应点分别为A’(-1,2),B’(2,2),
∴-3a+m=-1,0+n=2,3a+m=2,,0+n=2,解得a=,m=,n=2.
设F的坐标为(x,y).∵对应点F′与点F重合,∴x+=x,y+2=y,解得x=1,y=4,则F的坐标为(1,4).
21世纪教育网(www.21cnjy.com)
