2021-2022学年鲁教版八年级数学下册《6-1菱形的性质与判定》寒假预习同步达标测评 (word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册《6-1菱形的性质与判定》寒假预习同步达标测评 (word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 434.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 08:30:00 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学下册《6-1菱形的性质与判定》
寒假预习同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )
A.cm B.2cm C.1cm D.2cm
2.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H.则DH=( )
A.6 B. C. D.5
3.如图,已知菱形ABCD的周长为24,对角线AC、BD交于点O,且AC+BD=16,则该菱形的面积等于( )
A.6 B.8 C.14 D.28
4.平行四边形ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC⊥BD B.∠ABD=∠CBD C.AB=BC D.AC=BD
5.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是( )
A.AC⊥BD B.BA⊥BD C.AB=CD D.AD=BC
6.下列选项中能使 ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
7.如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;
③AD=4AG;④4FH=BD;其中正确结论的是( )
A.①②③ B.①②④ C.①③④ D.②③④
8.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:①OG=AB;②S△ACD=6S△BOF;③由点A、B、D、E构成的四边形是菱形;④S四边形ODGF>S△ABF.其中正确的结论是( )
A.①② B.①②③ C.①③④ D.②③④
9.如图,锐角∠BOC=α,∠AOC是它的邻补角,AD∥OC,OD平分∠AOC,P为射线OC上一点(不含端点O),连接PD,作∠DPE=α,PE交直线AB于点E.甲、乙、丙、丁四位同学都对这个问题进行了研究,并得出自己的结论.
甲:若点E与点O重合,四边形PEAD是菱形;
乙:若α=60°,一定PD=PE;
丙:若α≠60°,一定PD≠PE;
丁:若α=80°,可能PD=PE.
下列判断正确的是( )
A.甲、乙、丙正确,丁不正确
B.甲、乙、丁正确,丙不正确
C.甲、乙正确,丙、丁不正确
D.甲、乙、丁不正确,丙正确
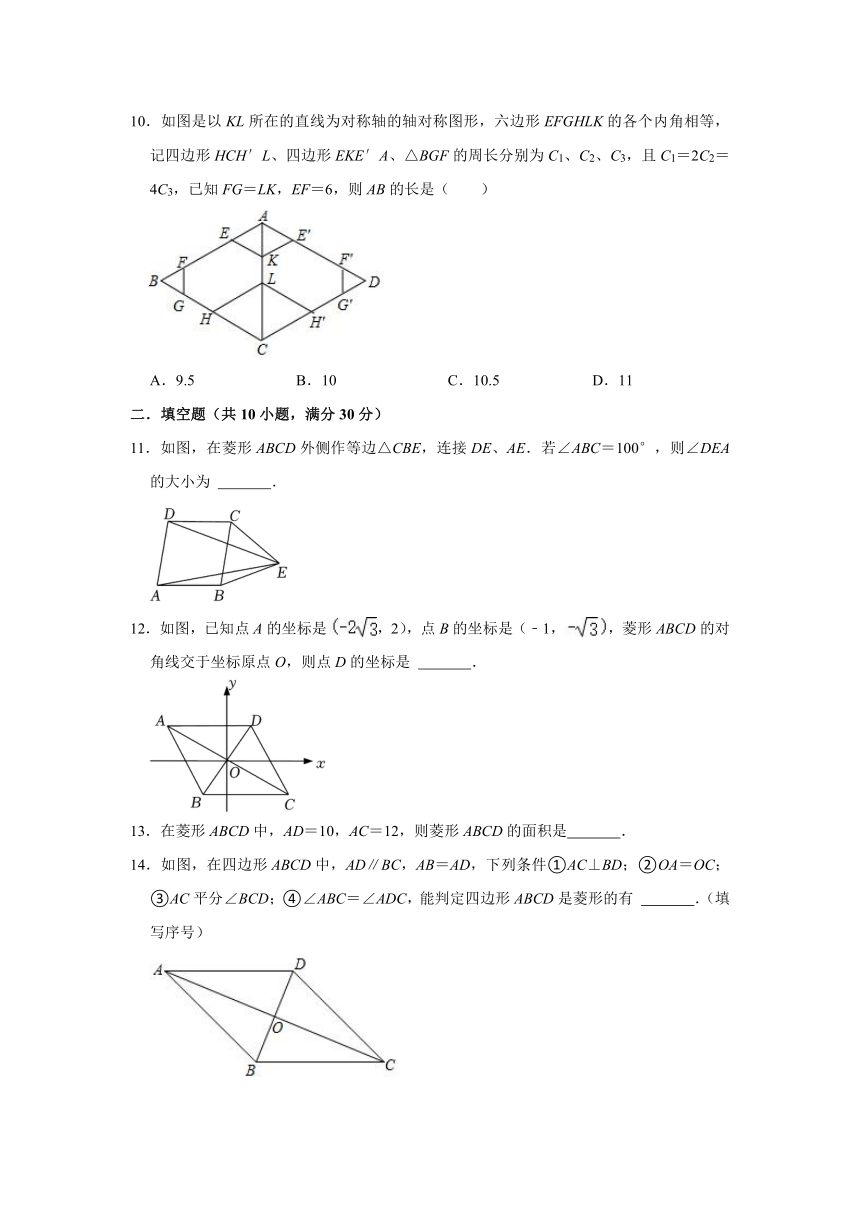
10.如图是以KL所在的直线为对称轴的轴对称图形,六边形EFGHLK的各个内角相等,记四边形HCH′L、四边形EKE′A、△BGF的周长分别为C1、C2、C3,且C1=2C2=4C3,已知FG=LK,EF=6,则AB的长是( )
A.9.5 B.10 C.10.5 D.11
二.填空题(共10小题,满分30分)
11.如图,在菱形ABCD外侧作等边△CBE,连接DE、AE.若∠ABC=100°,则∠DEA的大小为 .
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.在菱形ABCD中,AD=10,AC=12,则菱形ABCD的面积是 .
14.如图,在四边形ABCD中,AD∥BC,AB=AD,下列条件①AC⊥BD;②OA=OC;③AC平分∠BCD;④∠ABC=∠ADC,能判定四边形ABCD是菱形的有 .(填写序号)
15.如图,在 ABCD中,点E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是 .
16.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
17.如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接CF,DF,EF,∠ACB=90°,∠ABC=30°.有下列五个结论:①AC⊥DF;②DA+DF=BE;③四边形ADCF是菱形;④S四边形BCDE=6S△ACD;⑤四边形BCDF是平行四边形.其中正确的结论是
18.把2张大小形状完全相同的平行四边形纸片(如图1)按两种不同的方式(如图2、图3)不重叠地放在平行四边形ABCD内,未被覆盖的部分用阴影表示,若AD﹣AB=1,则图3中阴影部分的周长与图2中阴影部分的周长的差值是 .
19.如图,点E,F分别是矩形ABCD的边CD,AB的中点,两条平行线AK,CL分别经过菱形EGFH的顶点H,G和边FG,EH的中点M,N,已知菱形EGFH的面积为S,则图中阴影部分的面积和为 .(用含S的代数式表示)
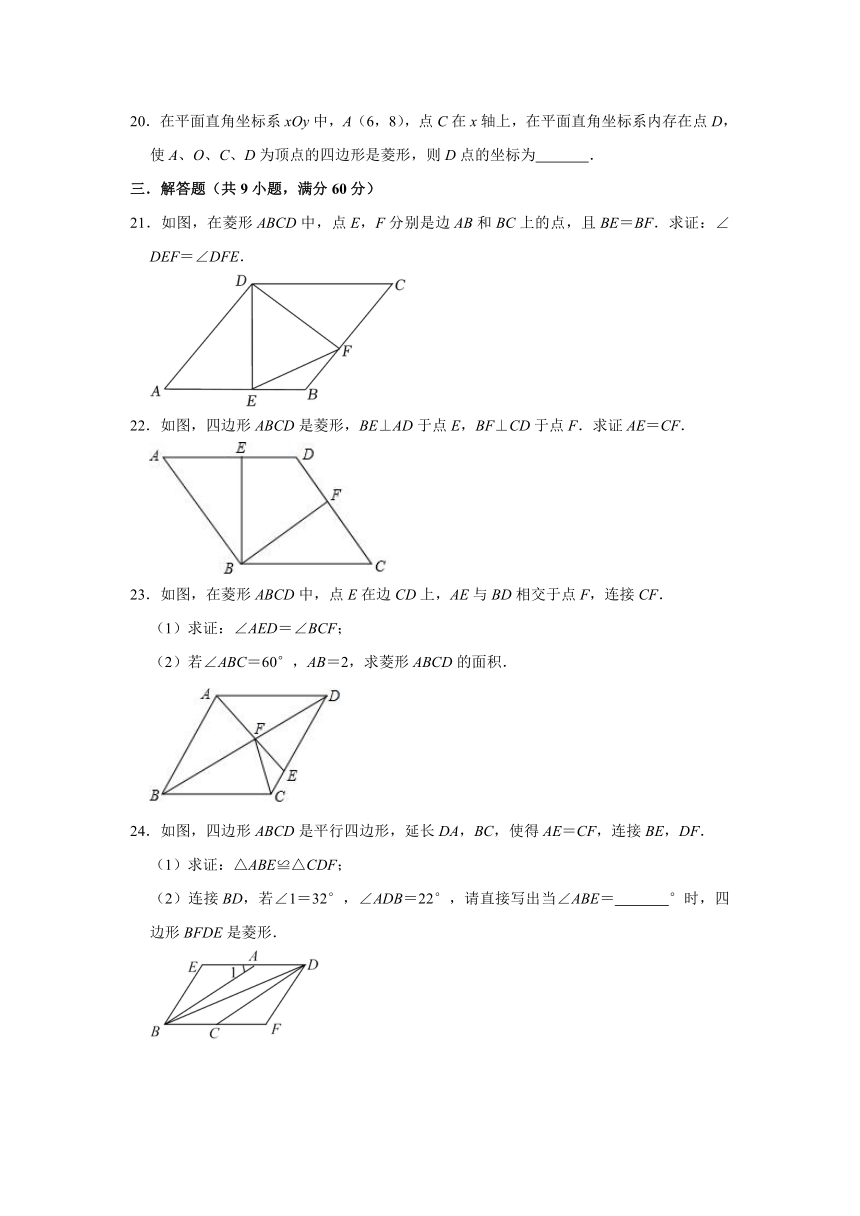
20.在平面直角坐标系xOy中,A(6,8),点C在x轴上,在平面直角坐标系内存在点D,使A、O、C、D为顶点的四边形是菱形,则D点的坐标为 .
三.解答题(共9小题,满分60分)
21.如图,在菱形ABCD中,点E,F分别是边AB和BC上的点,且BE=BF.求证:∠DEF=∠DFE.
22.如图,四边形ABCD是菱形,BE⊥AD于点E,BF⊥CD于点F.求证AE=CF.
23.如图,在菱形ABCD中,点E在边CD上,AE与BD相交于点F,连接CF.
(1)求证:∠AED=∠BCF;
(2)若∠ABC=60°,AB=2,求菱形ABCD的面积.
24.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
25.如图,在△ABC中,PQ是CA的垂直平分线,CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
26.如图,点E是 ABCD的边CD的中点,连接AE并延长,交BC的延长线于点F.
(1)若AD的长为2,求CF的长;
(2)若∠BAF=90°,则当∠F= 时,平行四边形ABCD是菱形.
27.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
28.如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点.
求证:四边形EGFH是菱形.
29.如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠BAC=∠CDF.
(1)求证:BC=2CE;
(2)求证:AM=DF+ME.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵菱形ABCD的周长为8cm,
∴AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2cm,
∴OA=1(cm),
在Rt△AOB中,由勾股定理得:OB===(cm),
∴BD=2OB=2(cm),
故选:B.
2.解:∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=3,AC⊥BD,
在Rt△AOB中,AB==5,
则AD=5,
∵S菱形ABCD= AC BD,
S菱形ABCD=DH AB,
∴DH 5=×6×8,
∴DH=.
故选:B.
3.解:∵四边形ABCD是菱形,
∴AC⊥BD,AB=BC=CD=DA,
∵菱形ABCD的周长为24,
∴AD=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴AO2+BO2+2AO BO=64,
∵AO2+BO2=AB2,
∴AO BO=14,
∴菱形的面积=4×三角形AOD的面积=4××14=28,
故选:D.
4.解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项D不符合题意;
故选:D.
5.解:能判定四边形ABCD是菱形的是AC⊥BD,理由如下:
∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,
故选:A.
6.解:A、∵四边形ABCD是平行四边形,
∴AB=CD,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,AB=BC,
∴ ABCD为菱形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,∠BAD=90°,
∴ ABCD为矩形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
7.解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠EAF=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
在△ABC和△EFA中,
,
∴△ABC≌△EFA(SAS),
∴FE=AB,∠AEF=∠BAC=30°,
∴∠AHE=180°﹣∠EAC﹣∠AEF=180°﹣60°﹣30°=90°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴FH∥BC,
∵F是AB的中点,
∴FH是△ABC的中位线,
∴FH=BC,
∵BC=AB,AB=BD,
∴BD=4FH,故④正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠FEA,
在△DBF和△EFA中,
,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB=AD,
∴四边形ADFE为平行四边形,
∵AB>AC,
∴AD>AE,
∴四边形ADFE不是菱形,故②错误;
∵AG=AF,
∴AG=AB,
∵AD=AB,
则AD=4AG,故③正确,
故选:C.
8.解:①∵四边形 ABCD 是菱形,
∴AB∥CD,AB=CD,BO=OD,
∴∠ABG=∠GED,∠BAG=∠GDE,
∵CD=DE,
∴AB=DE,
∴△ABG≌△DEG(AAS),
∴BG=GE,
∴OG=AB,∴①正确;
②由①知△ABG≌△DEG,
∴AG=GD,
∵四边形ABCD是菱形,
∴AB=AD,AO⊥BO,
∵∠BAD=60°,
∴AB=BD=AD,BG⊥AD,
∴∠FBO=30°,∠ABO=60°,∠BAO=30°,
∴,
∵S△ACD=S△ABC=2S△ABO,
∴,∴②正确
③由①知△ABG≌△DEG,
∴AB=DE,
∵AB∥DE,
∴四边形ABDE是平行四边形,
由②知:AB=BD,
∴四边形ABDE是菱形,∴③正确.
④∵BO=DO,AG=DG,
∴,OG∥AB,
∴S△AFG=2S△OFG,
∵S△AOG=S△AFG+S△OFG,
∴,S△DOG:S△DBA=1:4,S△FOG:S△FAB=1:4,
∴,
∵AG=GD,
∴S△AOG=S△GOD,
∴S四边形,
∴S四边形ODGF=S△FAB,∴④不正确.
综上所述①②③正确.
故选:B.
9.解法一:如图1,点E与点O重合.
∵AD∥OC,
∴∠A=∠BOC=α,
∵∠DPE=α,
∴∠DPE=∠A,即∠DPO=∠A,
∵∠AOD=∠POD,OD=OD,
∴△ADO≌△PDO,
∴PO=AO,PD=AD,
∵∠ADO=∠POD,∠AOD=∠POD,
∴∠ADO=∠AOD,
∴AO=AD,
∴PO=AO=AD=PD,
∴四边形POAD是菱形,即四边形PEAD是菱形,
解法二:可以证明,AO=AD,四边形PEAD是平行四边形,可得菱形.
故甲正确;
当α=60°时,则∠AOD=∠DOP=∠POB=60°.
如图2,点E在线段AO上,连接DE交OD于点F.
∵∠AOB=∠DPE=60°,∠OFE=∠PFD,
∵∠OFP=∠EFD,
∴△OFP∽△EFD,
∴∠PED=∠POD=60°,
∴∠PDE=60°=∠PED,
∴PD=PE;
如图3,点E在线段AO的延长线上,延长DO、PE交于点F,连接DE.
∵∠FOE=∠DPE=60°,∠EFO=∠DFP(公共角),
∵∠OFP=∠EFD(公共角),
∴△OFP∽△EFD,
∴∠POF=∠DEF=120°,
∴∠PED=60°,
∵∠DPE=60°,
∴∠PDE=60°=∠PED,
∴PD=PE.
故乙正确;
由甲的结论可知,当点E与点O重合时,四边形PEAD是菱形,
此时PD=PE,这与α是否等于60°无关,
故丙错误;
由甲的结论可知,当点E与点O重合时,PD=PE,这与锐角α的大小无关,
如图4,即使α=80°,也可能存在PD=PE的情况.
故丁正确.
故选:B.
10.解:∵六边形EFGHLK的各个内角相等,
∴该六边形的每个内角为120°,每个外角都是60°,
∴△BFG,△AEK,△CHL都是等边三角形,
∴∠B=∠BAC=∠ACB=60°,BF=FG,AE=AK,CL=HL,
∴△ABC是等边三角形,
∴AB=AC,即BF+FE+AE=AK+KL+CL,
又∵BF=FG=KL,
∴EF=CL=6=CH,
由轴对称可得,四边形HCH′L、四边形EKE′A都是菱形,
∵C1=2C2,
∴AE=CH=3,
又∵2C2=4C3,
∴C3=C2=×12=6,
∴BF=×6=2,
∴AB=BF+EF+AE=2+6+3=11,
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵四边形ABCD是菱形,
∴AB=BC=CD,AB∥CD,
∴∠BCD=180°﹣∠ABC=80°,
∵△CBE是等边三角形,
∴BC=BE=CE,∠CBE=∠BCE=∠BEC=60°,
∴AB=BE,CD=CE,∠DCE=140°,∠ABE=160°,
∴∠CED=∠CDE=(180°﹣∠DCE)=20°,∠BAE=∠BEA=(180°﹣160°)=10°,
∴∠DEA=∠BEC﹣∠DEC﹣∠BEA=30°,
故答案为:30°.
12.解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,﹣),
∴D点坐标为(1,),
故答案为:(1,).
13.解:如图,连接AC,BD交于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=6,
∴∠AOD=90°,
∴OD==8,
∴BD=2OD=16,
∴S菱形ABCD=×AC×BD=×12×16=96,
故答案为96.
14.解:①∵AB=AD,AC⊥BD,
∴OB=OD,
∵AD∥BC,
∴∠ADO=∠CBO,
又∵∠AOD=∠COB,
∴△AOD≌△COB(ASA),
∴AD=CB,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴平行四边形ABCD是菱形,故①能判定四边形ABCD是菱形;
②∵AB=AD,AC⊥BD,
∴OB=OD,
∵OA=OC,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴平行四边形ABCD是菱形,故②能判定四边形ABCD是菱形;
③∵AD∥BC,
∴∠DAC=∠BCA,
∵AC平分∠BCD,
∴∠DCA=∠BCA,
∴∠DAC=∠DCA,
∴AD=CD,
∴AB=AD=CD,不能判定四边形ABCD是菱形;
④∵AD∥BC,
∴∠BAD+∠ABC=180°,
∵∠ABC=∠ADC,
∴∠BAD+∠ADC=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴平行四边形ABCD是菱形,故④能判定四边形ABCD是菱形;
故答案为:①②④.
15.解:添加BD⊥EF,理由如下:
∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,AB∥CD,AB=CD,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=CF,
∴AB﹣AE=CD﹣CF,
即BE=DF,
又∵BE∥DF,
∴四边形EBFD是平行四边形,
∵BD⊥EF,
∴四边形EBFD是菱形.
故答案为:BD⊥EF.
16.解:添加一个条件OA=OC,则四边形ABCD为菱形,理由如下:
∵AC平分BD,OA=OC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:OA=OC(答案不唯一).
17.解:∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,AC=AB,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴CD∥AB,
∵F为AB的中点,
∴BF=AF=AB,
∴BF∥CD,CD=BF=AF,
∴四边形BCDF为平行四边形,故⑤正确;四边形ADCF是平行四边形,
∵∠ACB=90°,AF=BF,
∴CF=AF=AB,
∴四边形ADCF是菱形,故③正确;
∵四边形BCDF为平行四边形,
∴DF∥BC,
又∵∠ACB=90°,
∴AC⊥DF,故①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB,
∴DA+DF>BE,故②错误;
设AC=x,则AB=2x,
∴S△ACD=x2,S△ACB=x2,S△ABE=x2,
∴==,故④错误;
故答案为:①③⑤.
18.解:设图1平行四边形的长边为y,短边为x,AD=m,AB=n,
∵四边形ABCD是平行四边形,
∴AB=CD=n,AD=BC=m,
∵AD﹣AB=1,
∴m﹣n=1,
∴图2中阴影部分的周长=2y+2(n﹣x)+2x+2(n﹣y)
=2y+2n﹣2x+2x+2n﹣2y
=4n,
图3中阴影部分的周长=2(n﹣x)+2y+2x+2(m﹣y)
=2n﹣2x+2y+2x+2m﹣2y
=2m+2n,
∴图3中阴影部分的周长﹣图2中阴影部分的周长=2m+2n﹣4n=2(m﹣n)=2×1=2,
故答案为:2.
19.解:如图,连接EF、GH交于点O,设EF交NG于点R,交AK于点T,连接AG,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠D=90°,
∵E、F分别是CD、AB的中点,
∴DE=CD,AF=AB,
∴DE=AF,
∵DE∥AF,
∴四边形ADEF是平行四边形,
∵∠D=90°,
∴四边形ADEF是矩形,
∴EF∥AD,EF=AD,∠AFE=90°,
∵四边形EGFH是菱形,
∴GH⊥EF,OG=OH=GH,
∴∠EOG=90°,
∴∠EOG=∠AFE,
∴GH∥AF,
∴∠GHM=∠FAM,
∵点M是FG的中点,
∴GM=FM,
在△HGM和△AFM中,
,
∴△HGM≌△AFM(AAS),
∴GH=AF,
∴GH=AB,
∵OG=AF,OE=OF,OG∥AF,
∴点G是矩形ADEF的中心,即A、G、E三点在同一条直线上,
∴AG=EG,
∵EF∥AD,
∴∠LAG=∠REG,
在△AGL和△EGR中,
,
∴△AGL≌△EGR(ASA),
∴AL=ER,
∵AK∥CL,AL∥CK,
∴四边形ALCK是平行四边形,
同理,四边形ALRT是平行四边形,
∴AL=RT=CK,
∴ER=RT,
同理可得,RT=FT,
∴ER=RT=FT=EF=AD,
∵菱形EGFH的面积为S,
∴EF GH=2S,
∴AD AB=4S,
∵AL=AD,
∴S ALCK=AL AB=AD AB=S,
∵S GMHN=S,
∴S阴影=S ALCK﹣S GMHN=S﹣S=S;
故答案为:S.
20.解:根据题意画图如下:
∵A(6,8),
∴OA==10,
当四边形AODC是菱形时,D(6,﹣8);
当四边形AOC′D′是菱形时,D′(16,8);
当四边形AOC″D″是菱形时,D″(﹣4,8),
综上所述,满足条件的点D的坐标为:(6,﹣8)、(16,8)、(﹣4,8).
故答案为:(6,﹣8)、(16,8)、(﹣4,8).
三.解答题(共9小题,满分60分)
21.证明:∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,
∴∠DEF=∠DFE.
22.证明:∵四边形ABCD是菱形,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴AE=CF.
23.解:(1)证明:∵四边形ABCD为菱形,
∴AB=BC,∠ABD=∠CBD,AB∥CD.
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴∠BAF=∠BCF,
∵AB∥CD,
∴∠BAP=∠AED.
∴∠AED=∠BCF;
(2)过点A作AG⊥BC,垂足为G,
∴∠AGB=90°.
∴∠ABC=60°,
∴∠BAG=30°.
∵AB=2,
∴BG=1.
∵在Rt△ABG中,AG2+BG2=AB2.
∴.
∴.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
25.证明:(1)PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA);
(2)∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形.
26.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CF,
∴∠DAE=∠CFE,∠ADE=∠FCE,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD=2;
(2)∠F=30°时,平行四边形ABCD是菱形.
证明:∵∠BAF=90°,∠F=30°,
∴AB=BF,
∵点E是 ABCD的边CD的中点,
∴AD=BC=CF,
∵BF=BC+CF=2AD,
∴AD=BF,
∴AB=AD,
∴平行四边形ABCD是菱形.
27.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF,
由(1)得:四边形DEBF是菱形,
∴DE=DF=BE,
∴AD=DE,
∵AD=AE,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
∵DE=BE,
∴∠EDB=∠EBD=∠AED=30°,
同理:∠FDB=∠FBD=30°,
即图2中四个度数为30°的角为∠EDB、∠EBD、∠FDB、∠FBD.
28.证明:∵点E、F、G、H分别是AB、CD、AC、BD的中点,
∴GF是△ADC的中位线,GE是△ABC的中位线,EH是△ABD的中位线,
∴GF∥AD,GF=AD,GE=BC,EH∥AD,EH=AD,
∴GF∥EH,GF=EH,
∴四边形EGFH是平行四边形,
又∵AD=BC,
∴GE=EH,
∴四边形EGFH是菱形.
29.证明:
(1)∵四边形ABCD为菱形,
∴AB∥CD,且BC=CD,
∴∠BAC=∠ACD,且∠BAC=∠CDF,
∴∠ACD=∠CDF,
∴CM=DM,
∵ME⊥CD,
∴CE=DE,
∴BC=CD=2CE;
(2)如图,分别延长AB,DF交于点G,
∵AB∥CD,
∴∠G=∠CDF=∠BAC,
∴MG=MA,
在△CDF和△BGF中
∴△CDF≌△BGF(AAS),
∴GF=DF,
在△CEM和△CFM中
∴△CEM≌△CFM(SAS),
∴ME=MF,
∴AM=GM=GF+MF=DF+ME.
寒假预习同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )
A.cm B.2cm C.1cm D.2cm
2.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H.则DH=( )
A.6 B. C. D.5
3.如图,已知菱形ABCD的周长为24,对角线AC、BD交于点O,且AC+BD=16,则该菱形的面积等于( )
A.6 B.8 C.14 D.28
4.平行四边形ABCD的对角线AC与BD相交于点O,添加以下条件,不能判定平行四边形ABCD为菱形的是( )
A.AC⊥BD B.∠ABD=∠CBD C.AB=BC D.AC=BD
5.如图,四边形ABCD是平行四边形,下列说法能判定四边形ABCD是菱形的是( )
A.AC⊥BD B.BA⊥BD C.AB=CD D.AD=BC
6.下列选项中能使 ABCD成为菱形的是( )
A.AB=CD B.AB=BC C.∠BAD=90° D.AC=BD
7.如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°,给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;
③AD=4AG;④4FH=BD;其中正确结论的是( )
A.①②③ B.①②④ C.①③④ D.②③④
8.如图,菱形ABCD中,∠BAD=60°,AC与BD交于点O,E为CD延长线上的一点,且CD=DE,连结BE,分别交AC,AD于点F、G,连结OG,则下列结论:①OG=AB;②S△ACD=6S△BOF;③由点A、B、D、E构成的四边形是菱形;④S四边形ODGF>S△ABF.其中正确的结论是( )
A.①② B.①②③ C.①③④ D.②③④
9.如图,锐角∠BOC=α,∠AOC是它的邻补角,AD∥OC,OD平分∠AOC,P为射线OC上一点(不含端点O),连接PD,作∠DPE=α,PE交直线AB于点E.甲、乙、丙、丁四位同学都对这个问题进行了研究,并得出自己的结论.
甲:若点E与点O重合,四边形PEAD是菱形;
乙:若α=60°,一定PD=PE;
丙:若α≠60°,一定PD≠PE;
丁:若α=80°,可能PD=PE.
下列判断正确的是( )
A.甲、乙、丙正确,丁不正确
B.甲、乙、丁正确,丙不正确
C.甲、乙正确,丙、丁不正确
D.甲、乙、丁不正确,丙正确
10.如图是以KL所在的直线为对称轴的轴对称图形,六边形EFGHLK的各个内角相等,记四边形HCH′L、四边形EKE′A、△BGF的周长分别为C1、C2、C3,且C1=2C2=4C3,已知FG=LK,EF=6,则AB的长是( )
A.9.5 B.10 C.10.5 D.11
二.填空题(共10小题,满分30分)
11.如图,在菱形ABCD外侧作等边△CBE,连接DE、AE.若∠ABC=100°,则∠DEA的大小为 .
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.在菱形ABCD中,AD=10,AC=12,则菱形ABCD的面积是 .
14.如图,在四边形ABCD中,AD∥BC,AB=AD,下列条件①AC⊥BD;②OA=OC;③AC平分∠BCD;④∠ABC=∠ADC,能判定四边形ABCD是菱形的有 .(填写序号)
15.如图,在 ABCD中,点E,F分别是AB,CD边上的点,且∠ADE=∠CBF,连接BD,EF.补充一个条件,可使四边形EBFD是菱形,这个条件是 .
16.如图,四边形ABCD的对角线AC与BD交于点O,AC⊥BD,且AC平分BD,若添加一个条件 ,则四边形ABCD为菱形.
17.如图所示,分别以Rt△ABC的直角边AC,斜边AB为边向△ABC外构造等边△ACD和等边△ABE,F为AB的中点,连接CF,DF,EF,∠ACB=90°,∠ABC=30°.有下列五个结论:①AC⊥DF;②DA+DF=BE;③四边形ADCF是菱形;④S四边形BCDE=6S△ACD;⑤四边形BCDF是平行四边形.其中正确的结论是
18.把2张大小形状完全相同的平行四边形纸片(如图1)按两种不同的方式(如图2、图3)不重叠地放在平行四边形ABCD内,未被覆盖的部分用阴影表示,若AD﹣AB=1,则图3中阴影部分的周长与图2中阴影部分的周长的差值是 .
19.如图,点E,F分别是矩形ABCD的边CD,AB的中点,两条平行线AK,CL分别经过菱形EGFH的顶点H,G和边FG,EH的中点M,N,已知菱形EGFH的面积为S,则图中阴影部分的面积和为 .(用含S的代数式表示)
20.在平面直角坐标系xOy中,A(6,8),点C在x轴上,在平面直角坐标系内存在点D,使A、O、C、D为顶点的四边形是菱形,则D点的坐标为 .
三.解答题(共9小题,满分60分)
21.如图,在菱形ABCD中,点E,F分别是边AB和BC上的点,且BE=BF.求证:∠DEF=∠DFE.
22.如图,四边形ABCD是菱形,BE⊥AD于点E,BF⊥CD于点F.求证AE=CF.
23.如图,在菱形ABCD中,点E在边CD上,AE与BD相交于点F,连接CF.
(1)求证:∠AED=∠BCF;
(2)若∠ABC=60°,AB=2,求菱形ABCD的面积.
24.如图,四边形ABCD是平行四边形,延长DA,BC,使得AE=CF,连接BE,DF.
(1)求证:△ABE≌△CDF;
(2)连接BD,若∠1=32°,∠ADB=22°,请直接写出当∠ABE= °时,四边形BFDE是菱形.
25.如图,在△ABC中,PQ是CA的垂直平分线,CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
26.如图,点E是 ABCD的边CD的中点,连接AE并延长,交BC的延长线于点F.
(1)若AD的长为2,求CF的长;
(2)若∠BAF=90°,则当∠F= 时,平行四边形ABCD是菱形.
27.已知:在 ABCD中,对角线AC与BD交于点O,过点O作EF⊥BD,分别交AB,DC于点E,F,连接BF,DE.
(1)如图1,求证:四边形DEBF是菱形;
(2)如图2,AD∥EF,且AD=AE,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.
28.如图,在四边形ABCD中,AD=BC,点E、F、G、H分别是AB、CD、AC、BD的中点.
求证:四边形EGFH是菱形.
29.如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠BAC=∠CDF.
(1)求证:BC=2CE;
(2)求证:AM=DF+ME.
参考答案
一.选择题(共10小题,满分30分)
1.解:∵菱形ABCD的周长为8cm,
∴AB=BC=2(cm),OA=OC,OB=OD,AC⊥BD,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AC=AB=2cm,
∴OA=1(cm),
在Rt△AOB中,由勾股定理得:OB===(cm),
∴BD=2OB=2(cm),
故选:B.
2.解:∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=3,AC⊥BD,
在Rt△AOB中,AB==5,
则AD=5,
∵S菱形ABCD= AC BD,
S菱形ABCD=DH AB,
∴DH 5=×6×8,
∴DH=.
故选:B.
3.解:∵四边形ABCD是菱形,
∴AC⊥BD,AB=BC=CD=DA,
∵菱形ABCD的周长为24,
∴AD=AB=6,
∵AC+BD=16,
∴AO+BO=8,
∴AO2+BO2+2AO BO=64,
∵AO2+BO2=AB2,
∴AO BO=14,
∴菱形的面积=4×三角形AOD的面积=4××14=28,
故选:D.
4.解:A、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠CDB,
又∵∠ABD=∠CBD,
∴∠CDB=∠CBD,
∴BC=DC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形,故选项D不符合题意;
故选:D.
5.解:能判定四边形ABCD是菱形的是AC⊥BD,理由如下:
∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,
故选:A.
6.解:A、∵四边形ABCD是平行四边形,
∴AB=CD,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,AB=BC,
∴ ABCD为菱形,故选项B符合题意;
C、∵四边形ABCD是平行四边形,∠BAD=90°,
∴ ABCD为矩形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,AC=BD,
∴ ABCD为矩形,故选项D不符合题意;
故选:B.
7.解:∵△ACE是等边三角形,
∴∠EAC=60°,AE=AC,
∵∠BAC=30°,
∴∠EAF=∠ACB=90°,AB=2BC,
∵F为AB的中点,
∴AB=2AF,
∴BC=AF,
在△ABC和△EFA中,
,
∴△ABC≌△EFA(SAS),
∴FE=AB,∠AEF=∠BAC=30°,
∴∠AHE=180°﹣∠EAC﹣∠AEF=180°﹣60°﹣30°=90°,
∴EF⊥AC,故①正确,
∵EF⊥AC,∠ACB=90°,
∴FH∥BC,
∵F是AB的中点,
∴FH是△ABC的中位线,
∴FH=BC,
∵BC=AB,AB=BD,
∴BD=4FH,故④正确;
∵AD=BD,BF=AF,
∴∠DFB=90°,∠BDF=30°,
∵∠FAE=90°,
∴∠DFB=∠EAF,
∵EF⊥AC,
∴∠AEF=30°,
∴∠BDF=∠FEA,
在△DBF和△EFA中,
,
∴△DBF≌△EFA(AAS),
∴AE=DF,
∵FE=AB=AD,
∴四边形ADFE为平行四边形,
∵AB>AC,
∴AD>AE,
∴四边形ADFE不是菱形,故②错误;
∵AG=AF,
∴AG=AB,
∵AD=AB,
则AD=4AG,故③正确,
故选:C.
8.解:①∵四边形 ABCD 是菱形,
∴AB∥CD,AB=CD,BO=OD,
∴∠ABG=∠GED,∠BAG=∠GDE,
∵CD=DE,
∴AB=DE,
∴△ABG≌△DEG(AAS),
∴BG=GE,
∴OG=AB,∴①正确;
②由①知△ABG≌△DEG,
∴AG=GD,
∵四边形ABCD是菱形,
∴AB=AD,AO⊥BO,
∵∠BAD=60°,
∴AB=BD=AD,BG⊥AD,
∴∠FBO=30°,∠ABO=60°,∠BAO=30°,
∴,
∵S△ACD=S△ABC=2S△ABO,
∴,∴②正确
③由①知△ABG≌△DEG,
∴AB=DE,
∵AB∥DE,
∴四边形ABDE是平行四边形,
由②知:AB=BD,
∴四边形ABDE是菱形,∴③正确.
④∵BO=DO,AG=DG,
∴,OG∥AB,
∴S△AFG=2S△OFG,
∵S△AOG=S△AFG+S△OFG,
∴,S△DOG:S△DBA=1:4,S△FOG:S△FAB=1:4,
∴,
∵AG=GD,
∴S△AOG=S△GOD,
∴S四边形,
∴S四边形ODGF=S△FAB,∴④不正确.
综上所述①②③正确.
故选:B.
9.解法一:如图1,点E与点O重合.
∵AD∥OC,
∴∠A=∠BOC=α,
∵∠DPE=α,
∴∠DPE=∠A,即∠DPO=∠A,
∵∠AOD=∠POD,OD=OD,
∴△ADO≌△PDO,
∴PO=AO,PD=AD,
∵∠ADO=∠POD,∠AOD=∠POD,
∴∠ADO=∠AOD,
∴AO=AD,
∴PO=AO=AD=PD,
∴四边形POAD是菱形,即四边形PEAD是菱形,
解法二:可以证明,AO=AD,四边形PEAD是平行四边形,可得菱形.
故甲正确;
当α=60°时,则∠AOD=∠DOP=∠POB=60°.
如图2,点E在线段AO上,连接DE交OD于点F.
∵∠AOB=∠DPE=60°,∠OFE=∠PFD,
∵∠OFP=∠EFD,
∴△OFP∽△EFD,
∴∠PED=∠POD=60°,
∴∠PDE=60°=∠PED,
∴PD=PE;
如图3,点E在线段AO的延长线上,延长DO、PE交于点F,连接DE.
∵∠FOE=∠DPE=60°,∠EFO=∠DFP(公共角),
∵∠OFP=∠EFD(公共角),
∴△OFP∽△EFD,
∴∠POF=∠DEF=120°,
∴∠PED=60°,
∵∠DPE=60°,
∴∠PDE=60°=∠PED,
∴PD=PE.
故乙正确;
由甲的结论可知,当点E与点O重合时,四边形PEAD是菱形,
此时PD=PE,这与α是否等于60°无关,
故丙错误;
由甲的结论可知,当点E与点O重合时,PD=PE,这与锐角α的大小无关,
如图4,即使α=80°,也可能存在PD=PE的情况.
故丁正确.
故选:B.
10.解:∵六边形EFGHLK的各个内角相等,
∴该六边形的每个内角为120°,每个外角都是60°,
∴△BFG,△AEK,△CHL都是等边三角形,
∴∠B=∠BAC=∠ACB=60°,BF=FG,AE=AK,CL=HL,
∴△ABC是等边三角形,
∴AB=AC,即BF+FE+AE=AK+KL+CL,
又∵BF=FG=KL,
∴EF=CL=6=CH,
由轴对称可得,四边形HCH′L、四边形EKE′A都是菱形,
∵C1=2C2,
∴AE=CH=3,
又∵2C2=4C3,
∴C3=C2=×12=6,
∴BF=×6=2,
∴AB=BF+EF+AE=2+6+3=11,
故选:D.
二.填空题(共10小题,满分30分)
11.解:∵四边形ABCD是菱形,
∴AB=BC=CD,AB∥CD,
∴∠BCD=180°﹣∠ABC=80°,
∵△CBE是等边三角形,
∴BC=BE=CE,∠CBE=∠BCE=∠BEC=60°,
∴AB=BE,CD=CE,∠DCE=140°,∠ABE=160°,
∴∠CED=∠CDE=(180°﹣∠DCE)=20°,∠BAE=∠BEA=(180°﹣160°)=10°,
∴∠DEA=∠BEC﹣∠DEC﹣∠BEA=30°,
故答案为:30°.
12.解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,﹣),
∴D点坐标为(1,),
故答案为:(1,).
13.解:如图,连接AC,BD交于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=6,
∴∠AOD=90°,
∴OD==8,
∴BD=2OD=16,
∴S菱形ABCD=×AC×BD=×12×16=96,
故答案为96.
14.解:①∵AB=AD,AC⊥BD,
∴OB=OD,
∵AD∥BC,
∴∠ADO=∠CBO,
又∵∠AOD=∠COB,
∴△AOD≌△COB(ASA),
∴AD=CB,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴平行四边形ABCD是菱形,故①能判定四边形ABCD是菱形;
②∵AB=AD,AC⊥BD,
∴OB=OD,
∵OA=OC,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴平行四边形ABCD是菱形,故②能判定四边形ABCD是菱形;
③∵AD∥BC,
∴∠DAC=∠BCA,
∵AC平分∠BCD,
∴∠DCA=∠BCA,
∴∠DAC=∠DCA,
∴AD=CD,
∴AB=AD=CD,不能判定四边形ABCD是菱形;
④∵AD∥BC,
∴∠BAD+∠ABC=180°,
∵∠ABC=∠ADC,
∴∠BAD+∠ADC=180°,
∴AB∥CD,
∴四边形ABCD是平行四边形,
又∵AB=AD,
∴平行四边形ABCD是菱形,故④能判定四边形ABCD是菱形;
故答案为:①②④.
15.解:添加BD⊥EF,理由如下:
∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,AB∥CD,AB=CD,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(ASA),
∴AE=CF,
∴AB﹣AE=CD﹣CF,
即BE=DF,
又∵BE∥DF,
∴四边形EBFD是平行四边形,
∵BD⊥EF,
∴四边形EBFD是菱形.
故答案为:BD⊥EF.
16.解:添加一个条件OA=OC,则四边形ABCD为菱形,理由如下:
∵AC平分BD,OA=OC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴平行四边形ABCD是菱形,
故答案为:OA=OC(答案不唯一).
17.解:∵∠ACB=90°,∠ABC=30°,
∴∠BAC=60°,AC=AB,
∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠ACD=∠BAC,
∴CD∥AB,
∵F为AB的中点,
∴BF=AF=AB,
∴BF∥CD,CD=BF=AF,
∴四边形BCDF为平行四边形,故⑤正确;四边形ADCF是平行四边形,
∵∠ACB=90°,AF=BF,
∴CF=AF=AB,
∴四边形ADCF是菱形,故③正确;
∵四边形BCDF为平行四边形,
∴DF∥BC,
又∵∠ACB=90°,
∴AC⊥DF,故①正确;
∵DA=CA,DF=BC,AB=BE,BC+AC>AB,
∴DA+DF>BE,故②错误;
设AC=x,则AB=2x,
∴S△ACD=x2,S△ACB=x2,S△ABE=x2,
∴==,故④错误;
故答案为:①③⑤.
18.解:设图1平行四边形的长边为y,短边为x,AD=m,AB=n,
∵四边形ABCD是平行四边形,
∴AB=CD=n,AD=BC=m,
∵AD﹣AB=1,
∴m﹣n=1,
∴图2中阴影部分的周长=2y+2(n﹣x)+2x+2(n﹣y)
=2y+2n﹣2x+2x+2n﹣2y
=4n,
图3中阴影部分的周长=2(n﹣x)+2y+2x+2(m﹣y)
=2n﹣2x+2y+2x+2m﹣2y
=2m+2n,
∴图3中阴影部分的周长﹣图2中阴影部分的周长=2m+2n﹣4n=2(m﹣n)=2×1=2,
故答案为:2.
19.解:如图,连接EF、GH交于点O,设EF交NG于点R,交AK于点T,连接AG,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,∠D=90°,
∵E、F分别是CD、AB的中点,
∴DE=CD,AF=AB,
∴DE=AF,
∵DE∥AF,
∴四边形ADEF是平行四边形,
∵∠D=90°,
∴四边形ADEF是矩形,
∴EF∥AD,EF=AD,∠AFE=90°,
∵四边形EGFH是菱形,
∴GH⊥EF,OG=OH=GH,
∴∠EOG=90°,
∴∠EOG=∠AFE,
∴GH∥AF,
∴∠GHM=∠FAM,
∵点M是FG的中点,
∴GM=FM,
在△HGM和△AFM中,
,
∴△HGM≌△AFM(AAS),
∴GH=AF,
∴GH=AB,
∵OG=AF,OE=OF,OG∥AF,
∴点G是矩形ADEF的中心,即A、G、E三点在同一条直线上,
∴AG=EG,
∵EF∥AD,
∴∠LAG=∠REG,
在△AGL和△EGR中,
,
∴△AGL≌△EGR(ASA),
∴AL=ER,
∵AK∥CL,AL∥CK,
∴四边形ALCK是平行四边形,
同理,四边形ALRT是平行四边形,
∴AL=RT=CK,
∴ER=RT,
同理可得,RT=FT,
∴ER=RT=FT=EF=AD,
∵菱形EGFH的面积为S,
∴EF GH=2S,
∴AD AB=4S,
∵AL=AD,
∴S ALCK=AL AB=AD AB=S,
∵S GMHN=S,
∴S阴影=S ALCK﹣S GMHN=S﹣S=S;
故答案为:S.
20.解:根据题意画图如下:
∵A(6,8),
∴OA==10,
当四边形AODC是菱形时,D(6,﹣8);
当四边形AOC′D′是菱形时,D′(16,8);
当四边形AOC″D″是菱形时,D″(﹣4,8),
综上所述,满足条件的点D的坐标为:(6,﹣8)、(16,8)、(﹣4,8).
故答案为:(6,﹣8)、(16,8)、(﹣4,8).
三.解答题(共9小题,满分60分)
21.证明:∵四边形ABCD是菱形,
∴∠A=∠C,AB=CB,AD=DC,
∵BE=BF,
∴AE=CF,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴DE=DF,
∴∠DEF=∠DFE.
22.证明:∵四边形ABCD是菱形,
∴BA=BC,∠A=∠C,
∵BE⊥AD,BF⊥CD,
∴∠BEA=∠BFC=90°,
在△ABE与△CBF中
,
∴△ABE≌△CBF(AAS),
∴AE=CF.
23.解:(1)证明:∵四边形ABCD为菱形,
∴AB=BC,∠ABD=∠CBD,AB∥CD.
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴∠BAF=∠BCF,
∵AB∥CD,
∴∠BAP=∠AED.
∴∠AED=∠BCF;
(2)过点A作AG⊥BC,垂足为G,
∴∠AGB=90°.
∴∠ABC=60°,
∴∠BAG=30°.
∵AB=2,
∴BG=1.
∵在Rt△ABG中,AG2+BG2=AB2.
∴.
∴.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠BCD,
∴∠1=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:当∠ABE=12°时,四边形BFDE是菱形,理由如下:
∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∴BF=DE,
∴四边形BFDE是平行四边形,
∵∠1=32°,∠ADB=22°,
∴∠ABD=∠1﹣∠ADB=10°,
∵∠ABE=12°,
∴∠DBE=∠ABD+∠ABE=22°,
∴∠DBE=∠ADB=22°,
∴BE=DE,
∴平行四边形BFDE是菱形,
故答案为:12.
25.证明:(1)PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB
∴∠EAC=∠FCA,∠CFD=∠AED,
在△AED与△CFD中,
,
∴△AED≌△CFD(ASA);
(2)∵△AED≌△CFD,
∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA,
∴EC=EA=FC=FA,
∴四边形AECF为菱形.
26.解:(1)∵四边形ABCD是平行四边形,
∴AD∥CF,
∴∠DAE=∠CFE,∠ADE=∠FCE,
∵点E是CD的中点,
∴DE=CE,
在△ADE和△FCE中,
,
∴△ADE≌△FCE(AAS),
∴CF=AD=2;
(2)∠F=30°时,平行四边形ABCD是菱形.
证明:∵∠BAF=90°,∠F=30°,
∴AB=BF,
∵点E是 ABCD的边CD的中点,
∴AD=BC=CF,
∵BF=BC+CF=2AD,
∴AD=BF,
∴AB=AD,
∴平行四边形ABCD是菱形.
27.(1)证明:∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
,
∴△BOE≌△DOF(ASA),
∴BE=DF,
∵BE∥DF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形;
(2)解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AD∥EF,
∴四边形ADFE是平行四边形,
∴AE=DF,
由(1)得:四边形DEBF是菱形,
∴DE=DF=BE,
∴AD=DE,
∵AD=AE,
∴AD=AE=DE,
∴△ADE是等边三角形,
∴∠AED=60°,
∵DE=BE,
∴∠EDB=∠EBD=∠AED=30°,
同理:∠FDB=∠FBD=30°,
即图2中四个度数为30°的角为∠EDB、∠EBD、∠FDB、∠FBD.
28.证明:∵点E、F、G、H分别是AB、CD、AC、BD的中点,
∴GF是△ADC的中位线,GE是△ABC的中位线,EH是△ABD的中位线,
∴GF∥AD,GF=AD,GE=BC,EH∥AD,EH=AD,
∴GF∥EH,GF=EH,
∴四边形EGFH是平行四边形,
又∵AD=BC,
∴GE=EH,
∴四边形EGFH是菱形.
29.证明:
(1)∵四边形ABCD为菱形,
∴AB∥CD,且BC=CD,
∴∠BAC=∠ACD,且∠BAC=∠CDF,
∴∠ACD=∠CDF,
∴CM=DM,
∵ME⊥CD,
∴CE=DE,
∴BC=CD=2CE;
(2)如图,分别延长AB,DF交于点G,
∵AB∥CD,
∴∠G=∠CDF=∠BAC,
∴MG=MA,
在△CDF和△BGF中
∴△CDF≌△BGF(AAS),
∴GF=DF,
在△CEM和△CFM中
∴△CEM≌△CFM(SAS),
∴ME=MF,
∴AM=GM=GF+MF=DF+ME.
