2021-2022学年鲁教版八年级数学下册《6-3正方形的判定与性质》寒假预习同步达标测评 (word版含解析))
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册《6-3正方形的判定与性质》寒假预习同步达标测评 (word版含解析)) |  | |
| 格式 | docx | ||
| 文件大小 | 261.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 08:34:37 | ||
图片预览




文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的判定与性质》
寒假预习同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.下列说法中正确的是( )
A.矩形的对角线平分每组对角 B.菱形的对角线相等且互相垂直
C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形
2.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
3.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
4.如图,四边形ABCD、CEFG均为正方形,其中正方形ABCD面积为8cm2,图中阴影部分面积为5cm2,正方形CEFG面积为( )
A.14cm2 B.16cm2 C.18cm2 D.20cm2
5.如图,O是正方形ABCD内一点,四边形OHBE与OGDF也都是正方形,图中阴影部分的面积是10,则EG长为( )
A. B. C.10 D.20
6.下列条件中,能判定四边形是正方形的是( )
A.对角线互相垂直且相等的四边形 B.对角线互相垂直的矩形
C.对角线相等的平行四边形 D.对角线互相平分且垂直的四边形
7.菱形,矩形,正方形都具有的性质是( )
A.四条边相等,四个角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
8.如图,正方形ABCD的边长为4,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则( )
A.S=6 B.S=8
C.S=10 D.S与BE长度有关
9.如图,正方形ABCD的边长为6,点E、F分别在BC和CD上,分别连接AE、AF、EF,若∠EAF=45°,EC=3,则CF的长为( )
A.3 B.4 C.5 D.6
10.如图所示,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF;⑤∠BAE=∠AFB
其中,正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共6小题,满分24分)
11.如图,正方形ABCD的边长为,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是
①∠DAE=∠DEA;②∠DMC=45°;③;④若MH=2,则S△CMD=
12.如图,以Rt△DEC的斜边向外作正方形ABCD,已知DE=12,DC=13,则BE= .
13.如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA=4,OB=3,点C,D在第一象限.则O、D两点的距离= .
14.如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是 .
15.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为8,则正方形ABCD的面积为 .
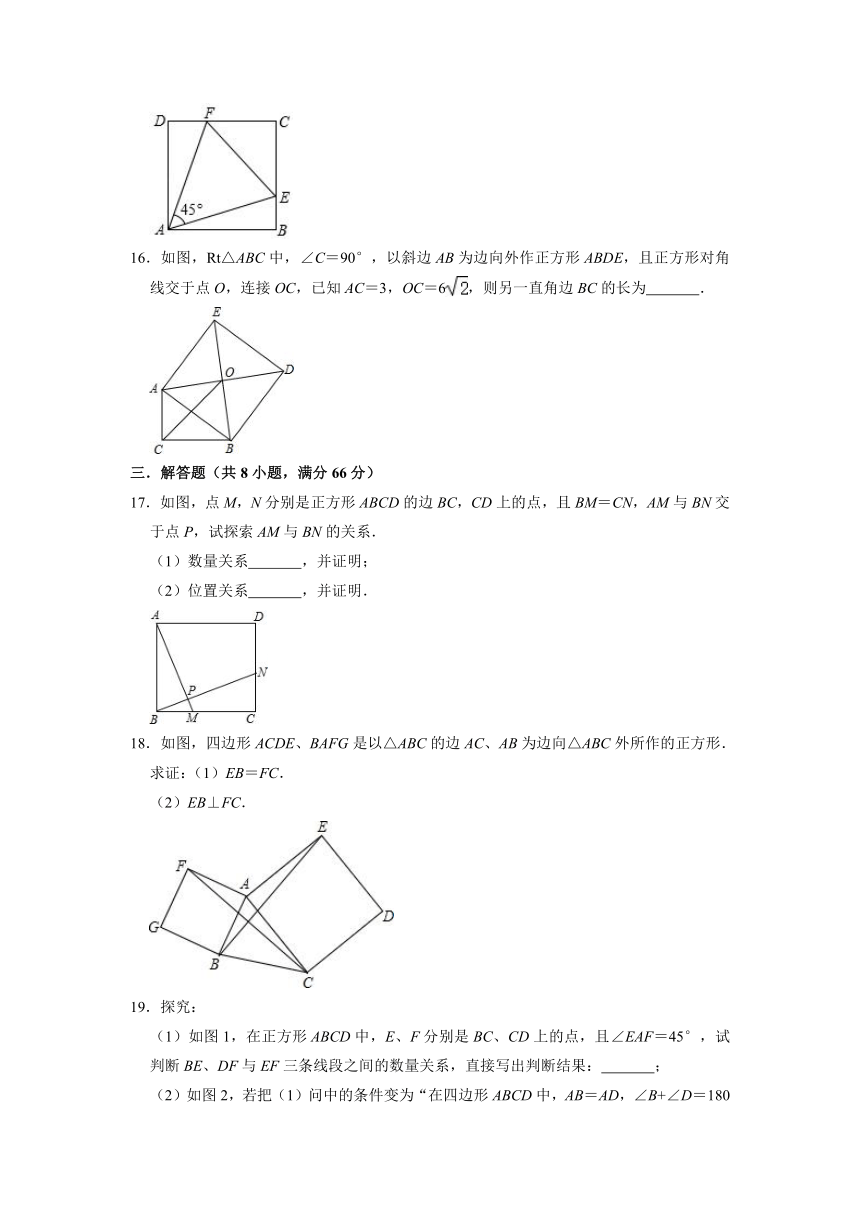
16.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=3,OC=6,则另一直角边BC的长为 .
三.解答题(共8小题,满分66分)
17.如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN,AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系 ,并证明;
(2)位置关系 ,并证明.
18.如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
求证:(1)EB=FC.
(2)EB⊥FC.
19.探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果: ;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.
20.如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=MF
(2)若AE=2,求FC的长.
21.如图,点E、F分别在正方形ABCD的边DA,AB上,且BE⊥CF于点G.
(1)求证:△ABE≌△BCF;
(2)若四边形AECF的面积为12,求BC的长.
22.如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,BE与AF相交于点O,P是BF的中点,连接OP.
(1)试判断AF与BE的关系,并证明你的结论;
(2)若AB=5,AE=2,求OP的长.
23.如图,正方形ABCD的边长为1,E为对角线BD上一点,且BE=BC,点P为线段CE上一动点,且PM⊥BE于点M,PN⊥BC于点N,求PM+PN的值.
24.如图,点E在正方形ABCD的边AB上,点F在边BC的延长线上,且∠EDF=90°.求证:DE=DF.
参考答案
一.选择题(共10小题,满分30分)
1.解:A、矩形的对角线平分每组对角,说法错误,故本选项不符合题意;
B、菱形的对角线互相垂直,故本选项不符合题意;
C、有一组邻边相等的矩形是正方形,正确,故本选项符合题意;
D、对角线互相垂直的四边形不一定是菱形,故本选项不符合题意.
故选:C.
2.解:因为矩形的四个角是直角,
故A正确,
因为菱形的对角线互相垂直,
故B正确,
因为正方形的对角线相等,
故C正确,
菱形的对角线和边长不一定相等,
例如:∠ABC=80°,因为AB=BC,所以∠BAC=∠ACB=50°,此时AC>AB,
故选:D.
3.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
4.解:∵阴影部分面积=DE×(BC+CG),
∴阴影部分面积=×(CE﹣DC)(BC+CG)=(CE2﹣BC2),
∵正方形ABCD面积为8cm2,图中阴影部分面积为5cm2,
∴5=(S正方形CEFG﹣8),
∴S正方形CEFG=18,
故选:C.
5.解:如图,连接AO,
∵四边形OHBE,四边形OGDF都是正方形,
∴FO=OG,HO=OE,
∵阴影部分的面积是10,
∴×OG×OF+×OE×OH=10,
∴OG2+OE2=20,
∴EG2=20,
∴EG=2,
故选:B.
6.解:A、对角线互相垂直且相等的四边形不一定的正方形,不符合题意;
B、对角线互相垂直的矩形是正方形,符合题意;
C、对角线相等的平行四边形是矩形,不符合题意;
D、对角线互相平分且垂直的四边形是菱形,不符合题意;
故选:B.
7.解:菱形,矩形,正方形都具有的性质为对角线互相平分.
故选:D.
8.解:设正方形EFGB的边长为a,
根据题意得:S=a2+16+a(4﹣a)﹣a(a+4)﹣×4×4=8.
故选:B.
9.解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
由旋转的性质得,HD=BE,AH=AE,∠DAH=∠BAE,
所以,∠FAH=∠DAH+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣∠EAF,
∵∠EAF=45°,
∴∠FAH=90°﹣45°=45°,
∴∠FAH=∠EAF,
在△AEF和△AHF中,
,
∴△AEF≌△AHF(SAS),
∴EF=FH,
∵EC=3,
∴BE=3,
∴HF=3+DF=EF,
∵EF2=FC2+EC2,
∴(3+DF)2=(6﹣DF)2+9,
∴DF=2,
∴FC=CD﹣DF=4,
故选:B.
10.解:在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,
∴AD﹣DF=CD﹣CE,即AF=DE,
在△ABF和△DAE中,,
∴△ABF≌△DAE(SAS),
∴AE=BF,故①正确;∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°﹣(∠ABF+∠BAO)=180°﹣90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,AO≠OE,故③错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
即S△AOB=S四边形DEOF,故④正确;
∵AE⊥BF,
∴∠AOB=90°.
∴∠OAB+∠ABO=90°.
又∵∠AFB+∠ABO=90°,
∴∠BAO=∠AFO,故⑤正确.
故选:C.
二.填空题(共6小题,满分24分)
11.解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵DC=DE,
∴DA=DE,
∴∠DAE=∠DEA,故①正确,
∵DA=DC=DE,
∴∠AEC=∠ADC=45°
∵DM⊥AE,
∴∠EHM=90°,
∴∠DMC=45°,故②正确,
如图,作DF⊥DM交PM于F,
∵∠ADC=∠MDF=90°,
∴∠ADM=∠CDF,
∵∠DMF=45°,
∴∠DMF=∠DFM=45°,
∴DM=DF,∵DA=DC,
∴△ADM≌△CDF(SAS),
∴AM=CF,
∴AM+CM=CF+CM=MF=DM,
∴=,故③正确,
若MH=2,则易知AH=MH=HE=2,AM=EM=2,
在Rt△ADH中,DH===1,
∴DM=3,AM+CM=3,
∴CM=CE=,
∴S△DCM=S△DCE,故④错误.
故选:①②③正确.
12.解:如图,过点B作BH⊥EC,交EC的延长线于H,
∴∠H=∠DEC=90°,
∵DE=12,DC=13,
∴EC===5,
∵四边形ABCD是正方形,
∴DC=BC,∠DCB=90°,
∴∠DCE+∠BCH=90°=∠DCE+∠CDE,
∴∠BCH=∠CDE,
在△DCE和△CBH中,
,
∴△DCE≌△CBH(AAS),
∴DE=12=CH,EC=BH=5,
∴EH=17,
∴BE===,
故答案为:.
13.解:如图,过点D作DF⊥OA于点F,
∵四边形ABCD是正方形
∴AD=AB,∠DAB=90°
∴∠DAF+∠BAO=90°,且∠BAO+∠ABO=90°
∴∠DAF=∠ABO,且AD=AB,∠DFA=∠AOB=90°
∴△DFA≌△AOB(AAS)
∴DF=AO=4,OB=AF=3
∴OF=OA+AF=7
∴OD==
故答案为:
14.解:过点D作DE⊥y轴,垂足为E.
∵A的坐标是(0,3),点B的坐标是(﹣4,0),
∴OA=3,OB=4.
∵ABCD为正方形,
∴AB=AD,∠DAB=90°.
∴∠DAE+∠BAO=∠ABO+∠BAO=90°,
∴∠DAE=∠ABO.
在△ABO和△DAE中,
,
∴△ABO≌△DAE.
∴AE=OB=4.
∴OE=AE+AO=4+3=7.
∴△OBD的面积=OB OE=×4×7=14.
故答案为:14.
15.解:将△DAF绕点A顺时针旋转90度到△BAF′位置,
由题意可得出:△DAF≌△BAF′,
∴DF=BF′,∠DAF=∠BAF′,
∴∠EAF′=45°,
在△FAE和△EAF′中,
,
∴△FAE≌△EAF′(SAS),
∴EF=EF′,
∵△ECF的周长=DF+EB+CF+CE=CD+CB=8,
∴AD=4,
∴正方形ABCD的面积为16.
故答案为:16.
16.解:过O作OF⊥BC于F,过A作AM⊥OF于M,
∵∠ACB=90°,
∴∠AMO=∠OFB=90°,∠ACB=∠CFM=∠AMF=90°,
∴四边形ACFM是矩形,
∴AM=CF,AC=MF=3,
∵四边形ABDE为正方形,
∴∠AOB=90°,OA=OB,
∴∠AOM+∠BOF=90°,
又∵∠AMO=90°,
∴∠AOM+∠OAM=90°,
∴∠BOF=∠OAM,
在△AOM和△OBF中,
∴△AOM≌△OBF(AAS),
∴AM=OF,OM=FB,
∴OF=CF,
∵∠CFO=90°,
∴△CFO是等腰直角三角形,
∵OC=6,由勾股定理得:CF=OF=6,
∴BF=OM=OF﹣FM=6﹣3=3,
∴BC=6+3=9.
故答案为:9.
三.解答题(共8小题,满分66分)
17.(1)解:AM=BN;理由如下:
∵四边形ABCD是正方形
∴∠ABM=∠BCN=90°,AB=BC,
在△ABM和△BCN中,,
∴△ABM≌△BCN(SAS),
∴AM=BN;故答案为:
(2)解:AM⊥BN;理由如下:
由(1)得:△ABM≌△BCN,
∴∠BAM=∠NBC,
∵∠NBC+∠ABN=∠ABC=90°,
∴∠BAM+∠ABN=90°,
在△ABP中,∠APB=180°﹣(∠BAM+∠ABN)=90°,
∴AM⊥BN;
故答案为:AM⊥BN.
18.证明:(1)∵四边形ACDE、BAFG都是正方形,
∴AB=AF,AC=AE,∠BAF=∠CAE=90°,
∴∠BAF+∠BAC=∠CAE+∠BAC,
即∠BAE=∠CAF,
在△ABE和△AFC中,,
∴△ABE≌△AFC(SAS),
∴EB=FC;
(2)∵△ABE≌△AFC,
∴∠AEB=∠ACF,
连接CE,设EB、CF相交于O,
则∠OEC+∠OCE=∠OEC+∠ACE+∠BEA=∠ACE+∠AEC=90°,
在△OCE中,∠COE=180°﹣(∠OEC+∠OCE)=180°﹣90°=90°,
∴EB⊥FC.
19.解:(1)如图1,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
∵∠EAF=45°,
∴∠EAF′=∠EAF=45°,
在△AEF和△AEF′中,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又EF′=BE+BF′=BE+DF,
∴EF=BE+DF;
(2)结论EF=BE+DF仍然成立.
理由如下:如图2,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
则△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,∠ABF′=∠D,
又∵∠EAF=∠BAD,
∴∠EAF=∠DAF+∠BAE=∠BAE+∠BAF′,
∴∠EAF=∠EAF′,
又∵∠ABC+∠D=180°,
∴∠ABF′+∠ABE=180°,
∴F′、B、E三点共线,
在△AEF与△AEF′中,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又∵EF′=BE+BF′,
∴EF=BE+DF;
(3)发生变化.EF、BE、DF之间的关系是EF=BE﹣DF.
理由如下:如图3,将△ADF绕点A顺时针旋转,使AD与AB重合,点F落在BC上点F′处,得到△ABF′,
∴△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,
又∵∠EAF=∠BAD,且∠BAF′=∠DAF,
∴∠F′AE=∠BAD﹣(∠BAF′+∠EAD)=∠BAD﹣(∠DAF+∠EAD)=∠BAD﹣∠FAE=∠FAE,
即∠F′AE=∠FAE,
在△F′AE与△FAE中,,
∴△F′AE≌△FAE(SAS),
∴EF=EF′,
又∵BE=BF′+EF′,
∴EF′=BE﹣BF′,
即EF=BE﹣DF.
20.解:(1)∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°.
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,∴∠FDM=∠EDF=45°,
∴△DEF≌△DMF(SAS),
∴EF=MF.
(2)设EF=MF=x,
∵AE=CM=2,且BC=6,∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4.
在Rt△EBF中,由勾股定理得EB2+BF2=EF2.
即42+(8﹣x)2=x2,
∴解得:x=5,即FM=5.
∴FC=FM﹣CM=5﹣2=3.
21.(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBF=90°,
∵BE⊥CF,
∴∠ABE+∠AEB=∠ABE+∠BFC=90°,
∴∠BFC=∠AEB.
在△ABE和△BCF中,
.
∴△ABE≌△BCF(AAS);
(2)解:∵△ABE≌△BCF,
∴S△ABE=S△BCF,
∴S△ABE﹣S△BFG=S△BCF﹣S△BFG,
∴S四边形AEGF=S△BGC,
∵四边形AECF的面积为12,
∴S△BCE=12.
∴正方形ABCD的面积是24.
∴BC==2.
22.解:(1)AF=BE,理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴AF=BE;
(2)由(1)知∴△BAE≌△ADF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AOE=∠BOF=90°,
∵点P为BF的中点,
∴OP=BF,
∵BC=AB=CD=5,AE=DF=2,
∴CF=CD﹣DF=5﹣2=3,
∴BF===,
∴OP=.
23.解:连接BP,作EF⊥BC于点F,则∠EFB=90°,
∵正方形的性质可知∠EBF=45°,
∴△BEF为等腰直角三角形,
∵正方形的边长为1,
∴BE=BC=1,
在直角三角形BEF中,sin∠EBF=,
∴BF=EF=BEsin45°=1×=,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
∴BE×PM+BC×PN=BC×EF,
∵BE=BC,
∴PM+PN=EF=.
24.证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠DCF=∠ADC=90°,
又∵∠EDF=90°,
∴∠ADC﹣∠EDC=∠EDF﹣∠EDC,
∴∠ADE=∠CDF,
在△ADE与△CDF中,
,
∴△ADE≌△CDF(ASA),
∴DE=DF.
寒假预习同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.下列说法中正确的是( )
A.矩形的对角线平分每组对角 B.菱形的对角线相等且互相垂直
C.有一组邻边相等的矩形是正方形 D.对角线互相垂直的四边形是菱形
2.如图,四边形ABCD是平行四边形,下列结论中错误的是( )
A.当 ABCD是矩形时,∠ABC=90° B.当 ABCD是菱形时,AC⊥BD
C.当 ABCD是正方形时,AC=BD D.当 ABCD是菱形时,AB=AC
3.如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
A.4 B.8 C.16 D.无法计算
4.如图,四边形ABCD、CEFG均为正方形,其中正方形ABCD面积为8cm2,图中阴影部分面积为5cm2,正方形CEFG面积为( )
A.14cm2 B.16cm2 C.18cm2 D.20cm2
5.如图,O是正方形ABCD内一点,四边形OHBE与OGDF也都是正方形,图中阴影部分的面积是10,则EG长为( )
A. B. C.10 D.20
6.下列条件中,能判定四边形是正方形的是( )
A.对角线互相垂直且相等的四边形 B.对角线互相垂直的矩形
C.对角线相等的平行四边形 D.对角线互相平分且垂直的四边形
7.菱形,矩形,正方形都具有的性质是( )
A.四条边相等,四个角相等 B.对角线相等
C.对角线互相垂直 D.对角线互相平分
8.如图,正方形ABCD的边长为4,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则( )
A.S=6 B.S=8
C.S=10 D.S与BE长度有关
9.如图,正方形ABCD的边长为6,点E、F分别在BC和CD上,分别连接AE、AF、EF,若∠EAF=45°,EC=3,则CF的长为( )
A.3 B.4 C.5 D.6
10.如图所示,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF;⑤∠BAE=∠AFB
其中,正确的有( )
A.2个 B.3个 C.4个 D.5个
二.填空题(共6小题,满分24分)
11.如图,正方形ABCD的边长为,E在正方形外,DE=DC,过D作DH⊥AE于H,直线DH,EC交于点M,直线CE交直线AD于点P,则下列结论正确的是
①∠DAE=∠DEA;②∠DMC=45°;③;④若MH=2,则S△CMD=
12.如图,以Rt△DEC的斜边向外作正方形ABCD,已知DE=12,DC=13,则BE= .
13.如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA=4,OB=3,点C,D在第一象限.则O、D两点的距离= .
14.如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是 .
15.如图,在正方形ABCD中,E、F分别是边BC、CD上的点,∠EAF=45°,△ECF的周长为8,则正方形ABCD的面积为 .
16.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=3,OC=6,则另一直角边BC的长为 .
三.解答题(共8小题,满分66分)
17.如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN,AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系 ,并证明;
(2)位置关系 ,并证明.
18.如图,四边形ACDE、BAFG是以△ABC的边AC、AB为边向△ABC外所作的正方形.
求证:(1)EB=FC.
(2)EB⊥FC.
19.探究:
(1)如图1,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,试判断BE、DF与EF三条线段之间的数量关系,直接写出判断结果: ;
(2)如图2,若把(1)问中的条件变为“在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD”,则(1)问中的结论是否仍然成立?若成立,请给出证明,若不成立,请说明理由;
(3)在(2)问中,若将△AEF绕点A逆时针旋转,当点分别E、F运动到BC、CD延长线上时,如图3所示,其它条件不变,则(1)问中的结论是否发生变化?若变化,请给出结论并予以证明.
20.如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=MF
(2)若AE=2,求FC的长.
21.如图,点E、F分别在正方形ABCD的边DA,AB上,且BE⊥CF于点G.
(1)求证:△ABE≌△BCF;
(2)若四边形AECF的面积为12,求BC的长.
22.如图,在正方形ABCD中,点E,F分别在AD,CD上,且AE=DF,BE与AF相交于点O,P是BF的中点,连接OP.
(1)试判断AF与BE的关系,并证明你的结论;
(2)若AB=5,AE=2,求OP的长.
23.如图,正方形ABCD的边长为1,E为对角线BD上一点,且BE=BC,点P为线段CE上一动点,且PM⊥BE于点M,PN⊥BC于点N,求PM+PN的值.
24.如图,点E在正方形ABCD的边AB上,点F在边BC的延长线上,且∠EDF=90°.求证:DE=DF.
参考答案
一.选择题(共10小题,满分30分)
1.解:A、矩形的对角线平分每组对角,说法错误,故本选项不符合题意;
B、菱形的对角线互相垂直,故本选项不符合题意;
C、有一组邻边相等的矩形是正方形,正确,故本选项符合题意;
D、对角线互相垂直的四边形不一定是菱形,故本选项不符合题意.
故选:C.
2.解:因为矩形的四个角是直角,
故A正确,
因为菱形的对角线互相垂直,
故B正确,
因为正方形的对角线相等,
故C正确,
菱形的对角线和边长不一定相等,
例如:∠ABC=80°,因为AB=BC,所以∠BAC=∠ACB=50°,此时AC>AB,
故选:D.
3.解:∵四边形ABCD是正方形,
∴∠ABC=∠D=90°,AB=AD,
即∠ABF=∠D=90°,
在Rt△ABF和Rt△ADE中,
,
∴Rt△ABF≌Rt△ADE(HL),
∴SRt△ABF=SRt△ADE,
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE,
∴S四边形AFCE=S正方形ABCD=16.
故选:C.
4.解:∵阴影部分面积=DE×(BC+CG),
∴阴影部分面积=×(CE﹣DC)(BC+CG)=(CE2﹣BC2),
∵正方形ABCD面积为8cm2,图中阴影部分面积为5cm2,
∴5=(S正方形CEFG﹣8),
∴S正方形CEFG=18,
故选:C.
5.解:如图,连接AO,
∵四边形OHBE,四边形OGDF都是正方形,
∴FO=OG,HO=OE,
∵阴影部分的面积是10,
∴×OG×OF+×OE×OH=10,
∴OG2+OE2=20,
∴EG2=20,
∴EG=2,
故选:B.
6.解:A、对角线互相垂直且相等的四边形不一定的正方形,不符合题意;
B、对角线互相垂直的矩形是正方形,符合题意;
C、对角线相等的平行四边形是矩形,不符合题意;
D、对角线互相平分且垂直的四边形是菱形,不符合题意;
故选:B.
7.解:菱形,矩形,正方形都具有的性质为对角线互相平分.
故选:D.
8.解:设正方形EFGB的边长为a,
根据题意得:S=a2+16+a(4﹣a)﹣a(a+4)﹣×4×4=8.
故选:B.
9.解:如图,将△ABE绕点A逆时针旋转90°得到△ADH,
由旋转的性质得,HD=BE,AH=AE,∠DAH=∠BAE,
所以,∠FAH=∠DAH+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=90°﹣∠EAF,
∵∠EAF=45°,
∴∠FAH=90°﹣45°=45°,
∴∠FAH=∠EAF,
在△AEF和△AHF中,
,
∴△AEF≌△AHF(SAS),
∴EF=FH,
∵EC=3,
∴BE=3,
∴HF=3+DF=EF,
∵EF2=FC2+EC2,
∴(3+DF)2=(6﹣DF)2+9,
∴DF=2,
∴FC=CD﹣DF=4,
故选:B.
10.解:在正方形ABCD中,∠BAF=∠D=90°,AB=AD=CD,
∵CE=DF,
∴AD﹣DF=CD﹣CE,即AF=DE,
在△ABF和△DAE中,,
∴△ABF≌△DAE(SAS),
∴AE=BF,故①正确;∠ABF=∠DAE,
∵∠DAE+∠BAO=90°,
∴∠ABF+∠BAO=90°,
在△ABO中,∠AOB=180°﹣(∠ABF+∠BAO)=180°﹣90°=90°,
∴AE⊥BF,故②正确;
假设AO=OE,
∵AE⊥BF(已证),
∴AB=BE(线段垂直平分线上的点到线段两端点的距离相等),
∵在Rt△BCE中,BE>BC,
∴AB>BC,这与正方形的边长AB=BC相矛盾,
所以,假设不成立,AO≠OE,故③错误;
∵△ABF≌△DAE,
∴S△ABF=S△DAE,
∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,
即S△AOB=S四边形DEOF,故④正确;
∵AE⊥BF,
∴∠AOB=90°.
∴∠OAB+∠ABO=90°.
又∵∠AFB+∠ABO=90°,
∴∠BAO=∠AFO,故⑤正确.
故选:C.
二.填空题(共6小题,满分24分)
11.解:∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵DC=DE,
∴DA=DE,
∴∠DAE=∠DEA,故①正确,
∵DA=DC=DE,
∴∠AEC=∠ADC=45°
∵DM⊥AE,
∴∠EHM=90°,
∴∠DMC=45°,故②正确,
如图,作DF⊥DM交PM于F,
∵∠ADC=∠MDF=90°,
∴∠ADM=∠CDF,
∵∠DMF=45°,
∴∠DMF=∠DFM=45°,
∴DM=DF,∵DA=DC,
∴△ADM≌△CDF(SAS),
∴AM=CF,
∴AM+CM=CF+CM=MF=DM,
∴=,故③正确,
若MH=2,则易知AH=MH=HE=2,AM=EM=2,
在Rt△ADH中,DH===1,
∴DM=3,AM+CM=3,
∴CM=CE=,
∴S△DCM=S△DCE,故④错误.
故选:①②③正确.
12.解:如图,过点B作BH⊥EC,交EC的延长线于H,
∴∠H=∠DEC=90°,
∵DE=12,DC=13,
∴EC===5,
∵四边形ABCD是正方形,
∴DC=BC,∠DCB=90°,
∴∠DCE+∠BCH=90°=∠DCE+∠CDE,
∴∠BCH=∠CDE,
在△DCE和△CBH中,
,
∴△DCE≌△CBH(AAS),
∴DE=12=CH,EC=BH=5,
∴EH=17,
∴BE===,
故答案为:.
13.解:如图,过点D作DF⊥OA于点F,
∵四边形ABCD是正方形
∴AD=AB,∠DAB=90°
∴∠DAF+∠BAO=90°,且∠BAO+∠ABO=90°
∴∠DAF=∠ABO,且AD=AB,∠DFA=∠AOB=90°
∴△DFA≌△AOB(AAS)
∴DF=AO=4,OB=AF=3
∴OF=OA+AF=7
∴OD==
故答案为:
14.解:过点D作DE⊥y轴,垂足为E.
∵A的坐标是(0,3),点B的坐标是(﹣4,0),
∴OA=3,OB=4.
∵ABCD为正方形,
∴AB=AD,∠DAB=90°.
∴∠DAE+∠BAO=∠ABO+∠BAO=90°,
∴∠DAE=∠ABO.
在△ABO和△DAE中,
,
∴△ABO≌△DAE.
∴AE=OB=4.
∴OE=AE+AO=4+3=7.
∴△OBD的面积=OB OE=×4×7=14.
故答案为:14.
15.解:将△DAF绕点A顺时针旋转90度到△BAF′位置,
由题意可得出:△DAF≌△BAF′,
∴DF=BF′,∠DAF=∠BAF′,
∴∠EAF′=45°,
在△FAE和△EAF′中,
,
∴△FAE≌△EAF′(SAS),
∴EF=EF′,
∵△ECF的周长=DF+EB+CF+CE=CD+CB=8,
∴AD=4,
∴正方形ABCD的面积为16.
故答案为:16.
16.解:过O作OF⊥BC于F,过A作AM⊥OF于M,
∵∠ACB=90°,
∴∠AMO=∠OFB=90°,∠ACB=∠CFM=∠AMF=90°,
∴四边形ACFM是矩形,
∴AM=CF,AC=MF=3,
∵四边形ABDE为正方形,
∴∠AOB=90°,OA=OB,
∴∠AOM+∠BOF=90°,
又∵∠AMO=90°,
∴∠AOM+∠OAM=90°,
∴∠BOF=∠OAM,
在△AOM和△OBF中,
∴△AOM≌△OBF(AAS),
∴AM=OF,OM=FB,
∴OF=CF,
∵∠CFO=90°,
∴△CFO是等腰直角三角形,
∵OC=6,由勾股定理得:CF=OF=6,
∴BF=OM=OF﹣FM=6﹣3=3,
∴BC=6+3=9.
故答案为:9.
三.解答题(共8小题,满分66分)
17.(1)解:AM=BN;理由如下:
∵四边形ABCD是正方形
∴∠ABM=∠BCN=90°,AB=BC,
在△ABM和△BCN中,,
∴△ABM≌△BCN(SAS),
∴AM=BN;故答案为:
(2)解:AM⊥BN;理由如下:
由(1)得:△ABM≌△BCN,
∴∠BAM=∠NBC,
∵∠NBC+∠ABN=∠ABC=90°,
∴∠BAM+∠ABN=90°,
在△ABP中,∠APB=180°﹣(∠BAM+∠ABN)=90°,
∴AM⊥BN;
故答案为:AM⊥BN.
18.证明:(1)∵四边形ACDE、BAFG都是正方形,
∴AB=AF,AC=AE,∠BAF=∠CAE=90°,
∴∠BAF+∠BAC=∠CAE+∠BAC,
即∠BAE=∠CAF,
在△ABE和△AFC中,,
∴△ABE≌△AFC(SAS),
∴EB=FC;
(2)∵△ABE≌△AFC,
∴∠AEB=∠ACF,
连接CE,设EB、CF相交于O,
则∠OEC+∠OCE=∠OEC+∠ACE+∠BEA=∠ACE+∠AEC=90°,
在△OCE中,∠COE=180°﹣(∠OEC+∠OCE)=180°﹣90°=90°,
∴EB⊥FC.
19.解:(1)如图1,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
∵∠EAF=45°,
∴∠EAF′=∠EAF=45°,
在△AEF和△AEF′中,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又EF′=BE+BF′=BE+DF,
∴EF=BE+DF;
(2)结论EF=BE+DF仍然成立.
理由如下:如图2,将△ADF绕点A顺时针旋转,使AD与AB重合,得到△ABF′,
则△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,∠ABF′=∠D,
又∵∠EAF=∠BAD,
∴∠EAF=∠DAF+∠BAE=∠BAE+∠BAF′,
∴∠EAF=∠EAF′,
又∵∠ABC+∠D=180°,
∴∠ABF′+∠ABE=180°,
∴F′、B、E三点共线,
在△AEF与△AEF′中,
,
∴△AEF≌△AEF′(SAS),
∴EF=EF′,
又∵EF′=BE+BF′,
∴EF=BE+DF;
(3)发生变化.EF、BE、DF之间的关系是EF=BE﹣DF.
理由如下:如图3,将△ADF绕点A顺时针旋转,使AD与AB重合,点F落在BC上点F′处,得到△ABF′,
∴△ADF≌△ABF′,
∴∠BAF′=∠DAF,AF′=AF,BF′=DF,
又∵∠EAF=∠BAD,且∠BAF′=∠DAF,
∴∠F′AE=∠BAD﹣(∠BAF′+∠EAD)=∠BAD﹣(∠DAF+∠EAD)=∠BAD﹣∠FAE=∠FAE,
即∠F′AE=∠FAE,
在△F′AE与△FAE中,,
∴△F′AE≌△FAE(SAS),
∴EF=EF′,
又∵BE=BF′+EF′,
∴EF′=BE﹣BF′,
即EF=BE﹣DF.
20.解:(1)∵△DAE逆时针旋转90°得到△DCM,
∴∠FCM=∠FCD+∠DCM=180°,
∴F、C、M三点共线,
∴DE=DM,∠EDM=90°.
∴∠EDF+∠FDM=90°,
∵∠EDF=45°,∴∠FDM=∠EDF=45°,
∴△DEF≌△DMF(SAS),
∴EF=MF.
(2)设EF=MF=x,
∵AE=CM=2,且BC=6,∴BM=BC+CM=6+2=8,
∴BF=BM﹣MF=BM﹣EF=8﹣x,
∵EB=AB﹣AE=6﹣2=4.
在Rt△EBF中,由勾股定理得EB2+BF2=EF2.
即42+(8﹣x)2=x2,
∴解得:x=5,即FM=5.
∴FC=FM﹣CM=5﹣2=3.
21.(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠A=∠CBF=90°,
∵BE⊥CF,
∴∠ABE+∠AEB=∠ABE+∠BFC=90°,
∴∠BFC=∠AEB.
在△ABE和△BCF中,
.
∴△ABE≌△BCF(AAS);
(2)解:∵△ABE≌△BCF,
∴S△ABE=S△BCF,
∴S△ABE﹣S△BFG=S△BCF﹣S△BFG,
∴S四边形AEGF=S△BGC,
∵四边形AECF的面积为12,
∴S△BCE=12.
∴正方形ABCD的面积是24.
∴BC==2.
22.解:(1)AF=BE,理由如下:
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
在△BAE和△ADF中,
,
∴△BAE≌△ADF(SAS),
∴AF=BE;
(2)由(1)知∴△BAE≌△ADF,
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AOE=∠BOF=90°,
∵点P为BF的中点,
∴OP=BF,
∵BC=AB=CD=5,AE=DF=2,
∴CF=CD﹣DF=5﹣2=3,
∴BF===,
∴OP=.
23.解:连接BP,作EF⊥BC于点F,则∠EFB=90°,
∵正方形的性质可知∠EBF=45°,
∴△BEF为等腰直角三角形,
∵正方形的边长为1,
∴BE=BC=1,
在直角三角形BEF中,sin∠EBF=,
∴BF=EF=BEsin45°=1×=,
∵PM⊥BD,PN⊥BC,
∴S△BPE+S△BPC=S△BEC,
∴BE×PM+BC×PN=BC×EF,
∵BE=BC,
∴PM+PN=EF=.
24.证明:∵四边形ABCD是正方形,
∴AD=CD,∠A=∠DCF=∠ADC=90°,
又∵∠EDF=90°,
∴∠ADC﹣∠EDC=∠EDF﹣∠EDC,
∴∠ADE=∠CDF,
在△ADE与△CDF中,
,
∴△ADE≌△CDF(ASA),
∴DE=DF.
