2021-2022学年 北师大版数学七年级下册3.2 用关系式表示的变量间关系同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年 北师大版数学七年级下册3.2 用关系式表示的变量间关系同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 311.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 08:40:52 | ||
图片预览



文档简介
北师大版数学七年级下同步练习:3.2用关系式表示的变量间关系
一、选择题
小军用 元钱去买单价是 元的笔记本,则他剩余的钱 (元)与他买这种笔记本的本数 之间的关系式是
A. B. C. D.
已知等腰三角形面积是 ,底边和底边上的高分别是 ,,则 与 的函数关系式是
A. B. C. D.
当 时,函数 的值是
A. B. C. D.
已知长方形的周长为 ,其中一边长为 ,面积为 ,则这个长方形的面积 与边长 之间的关系可以表示为
A. B.
C. D.
下列计算中正确的是
A. B.
C. D.
已知汽车油箱内有油 ,每行驶 耗油 ,那么汽车行驶过程中油箱内剩余的油量 与行驶路程 之间的关系式是
A. B. C. D.
已知 , 两地相距 ,小黄从 地到 地,平均速度为 ,若用 表示行走的时间(), 表示余下的路程(),则 关于 的函数解析式是
A. B.
C. D.
小明和他爸爸做了一个试验:由小明从一幢 高的楼顶随手扔下一只苹果,由他爸爸测量有关数据,得到苹果下落的路程和下落的时间有下面的关系:则下列说法错误的是
A.苹果每秒下落的路程不变
B.苹果每秒下落的路程越来越长
C.苹果下落的速度越来越快
D.可以推测,苹果下落 后到达地面
按图 的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为 张,摆放的椅子为 把,则 与 之间的关系式为
A. B. C. D.
如图,在四边形 中,,,.设 的长为 ,四边形 的面积 ,则 与 之间的函数关系式是
A. B. C. D.
如图,在 中,,且 ,设直线 截此三角形所得的阴影部分的面积为 ,则 与 之间的函数关系式为
A. B.
C. D.
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:科学家推测出 ()与 之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为
A. B. C. D.
某油箱容量为 的汽车,加满汽油后行驶了 ,此时油箱中的汽油大约消耗了 ,如果加满汽油后汽车行驶的路程为 ,油箱中剩油量为 ,则 与 之间的函数解析式和自变量的取值范围分别是
A. , B. ,
C. , D. ,
二、填空题
底面半径为 ,高为 的圆柱,两底的面积之和与圆柱的侧面积相等,则 与 的函数关系式为 .
如图,正方形 边长是 , 为 中点, 为正方形 边上的一个动点,动点 从 点出发,沿 运动,到达点 ,若点 经过的路程为自变量 , 的面积为函数 ,则当 时, 的值等于 .
日常生活中,“老人”是一个模糊概念.可用“老人系数”表示一个人的老年化程度,“老人系数”的计算方法如下表:按照这样的规定,“老人系数”为 的人的年龄是 岁.
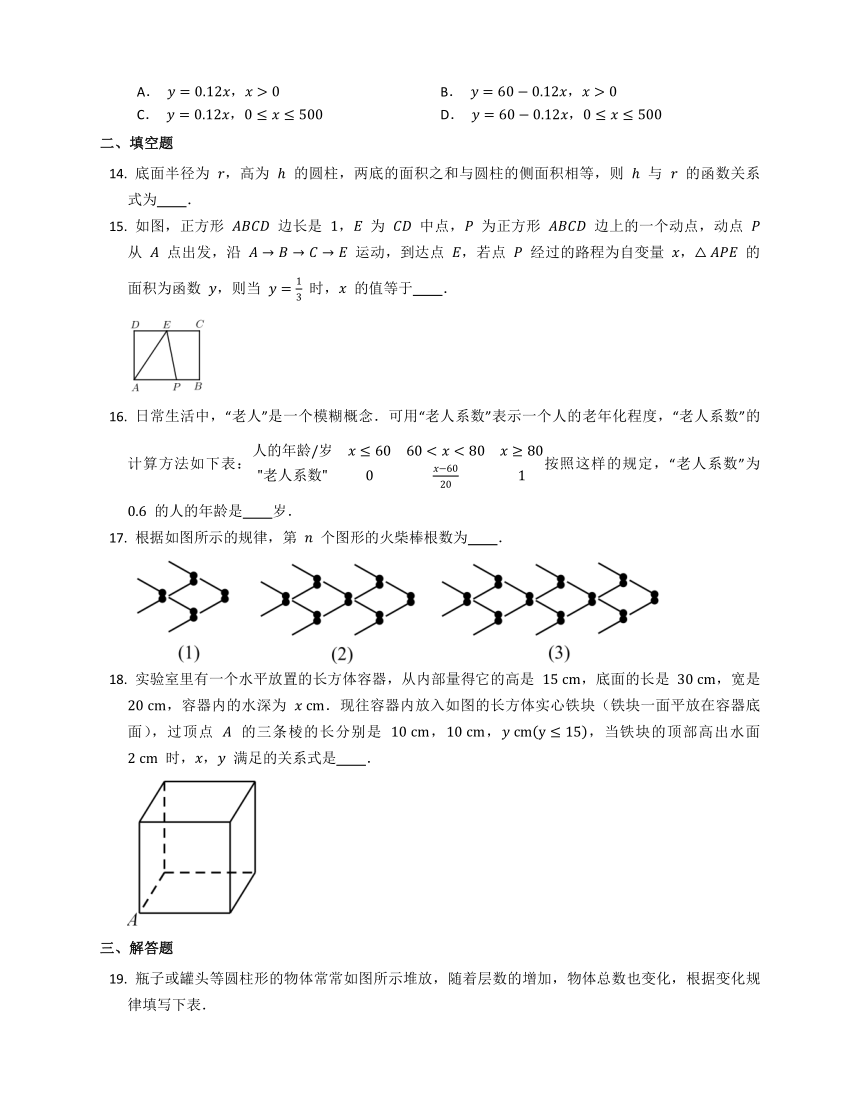
根据如图所示的规律,第 个图形的火柴棒根数为 .
实验室里有一个水平放置的长方体容器,从内部量得它的高是 ,底面的长是 ,宽是 ,容器内的水深为 .现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点 的三条棱的长分别是 ,,,当铁块的顶部高出水面 时,, 满足的关系式是 .
三、解答题
瓶子或罐头等圆柱形的物体常常如图所示堆放,随着层数的增加,物体总数也变化,根据变化规律填写下表.
则 与 的关系式是 ,其中变量是 ,常量是 .
在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁 辆客车前往宁波东站接员工返岗.已知现有A,B两种客车,A型客车的载客量为 人/辆,每辆租金为 元;B型客车的载客量为 人/辆,每辆租金为 元.设租用A型客车为 辆,所需用为 元.
(1) 求 关于 的函数解析式;
(2) 若该企业需要接的员工有 人,请求出租车费用最小值,并写出对应的租车方案.
已知 ,其中 表示当 时对应的函数值,如:
;
;
;
.
请根据该函数反映出的规律解决下列问题.
(1) 求 的值;
(2) 猜想: .
在平面直角坐标系 中,抛物线 过点 .
(1) 求抛物线的对称轴;
(2) 直线 与 轴交于点 ,与该抛物线的对称轴交于点 ,现将点 向左平移一个单位到点 ,如果该抛物线与线段 有交点,结合函数的图象,求 的取值范围.
答案
一、选择题
1.C 2.B 3.D 4.C 5.C 6.C 7.D 8.A 9.D 10.C 11.B 12.B 13.D
二、填空题
14.
15. 或
16.
17.
18. 或
三、解答题
19. ;;;;;;,;,
20.
(1) 设租用A型客车为 辆,则租用B型客车为 辆,由题意得 .
(2) 由题意得解得而费用 .
因为 为整数, 取最小时,费用 最低,
所以 ,.
所以方案为租用A型客车 辆,租用B型客车 辆.
21.
(1)
(2)
22.
(1) 把 代入 得:,
,
抛物线的对称轴为 .
(2) 由()可知,抛物线解析式为 ,对称轴为 ,
抛物线过点 ,.
当 时,,
.
当 时,如图.
由该抛物线与线段 有交点可得:当 时,,
即 ,解得:;
当 时,由题意得:,
,如图.
由该抛物线与线段 有交点可得:当 时,,
即 ,解得:.
综上所述, 的取值范围为 或 .
一、选择题
小军用 元钱去买单价是 元的笔记本,则他剩余的钱 (元)与他买这种笔记本的本数 之间的关系式是
A. B. C. D.
已知等腰三角形面积是 ,底边和底边上的高分别是 ,,则 与 的函数关系式是
A. B. C. D.
当 时,函数 的值是
A. B. C. D.
已知长方形的周长为 ,其中一边长为 ,面积为 ,则这个长方形的面积 与边长 之间的关系可以表示为
A. B.
C. D.
下列计算中正确的是
A. B.
C. D.
已知汽车油箱内有油 ,每行驶 耗油 ,那么汽车行驶过程中油箱内剩余的油量 与行驶路程 之间的关系式是
A. B. C. D.
已知 , 两地相距 ,小黄从 地到 地,平均速度为 ,若用 表示行走的时间(), 表示余下的路程(),则 关于 的函数解析式是
A. B.
C. D.
小明和他爸爸做了一个试验:由小明从一幢 高的楼顶随手扔下一只苹果,由他爸爸测量有关数据,得到苹果下落的路程和下落的时间有下面的关系:则下列说法错误的是
A.苹果每秒下落的路程不变
B.苹果每秒下落的路程越来越长
C.苹果下落的速度越来越快
D.可以推测,苹果下落 后到达地面
按图 的方式摆放餐桌和椅子,照这样的方式维续摆放,如果摆放的餐桌为 张,摆放的椅子为 把,则 与 之间的关系式为
A. B. C. D.
如图,在四边形 中,,,.设 的长为 ,四边形 的面积 ,则 与 之间的函数关系式是
A. B. C. D.
如图,在 中,,且 ,设直线 截此三角形所得的阴影部分的面积为 ,则 与 之间的函数关系式为
A. B.
C. D.
科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:科学家推测出 ()与 之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为
A. B. C. D.
某油箱容量为 的汽车,加满汽油后行驶了 ,此时油箱中的汽油大约消耗了 ,如果加满汽油后汽车行驶的路程为 ,油箱中剩油量为 ,则 与 之间的函数解析式和自变量的取值范围分别是
A. , B. ,
C. , D. ,
二、填空题
底面半径为 ,高为 的圆柱,两底的面积之和与圆柱的侧面积相等,则 与 的函数关系式为 .
如图,正方形 边长是 , 为 中点, 为正方形 边上的一个动点,动点 从 点出发,沿 运动,到达点 ,若点 经过的路程为自变量 , 的面积为函数 ,则当 时, 的值等于 .
日常生活中,“老人”是一个模糊概念.可用“老人系数”表示一个人的老年化程度,“老人系数”的计算方法如下表:按照这样的规定,“老人系数”为 的人的年龄是 岁.
根据如图所示的规律,第 个图形的火柴棒根数为 .
实验室里有一个水平放置的长方体容器,从内部量得它的高是 ,底面的长是 ,宽是 ,容器内的水深为 .现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点 的三条棱的长分别是 ,,,当铁块的顶部高出水面 时,, 满足的关系式是 .
三、解答题
瓶子或罐头等圆柱形的物体常常如图所示堆放,随着层数的增加,物体总数也变化,根据变化规律填写下表.
则 与 的关系式是 ,其中变量是 ,常量是 .
在“前线医护人员”和全国人民的共同努力下,疫情得到了有效控制,宁波各大企业复工复产有序进行.为了实现员工“一站式”返岗,宁波某企业打算租赁 辆客车前往宁波东站接员工返岗.已知现有A,B两种客车,A型客车的载客量为 人/辆,每辆租金为 元;B型客车的载客量为 人/辆,每辆租金为 元.设租用A型客车为 辆,所需用为 元.
(1) 求 关于 的函数解析式;
(2) 若该企业需要接的员工有 人,请求出租车费用最小值,并写出对应的租车方案.
已知 ,其中 表示当 时对应的函数值,如:
;
;
;
.
请根据该函数反映出的规律解决下列问题.
(1) 求 的值;
(2) 猜想: .
在平面直角坐标系 中,抛物线 过点 .
(1) 求抛物线的对称轴;
(2) 直线 与 轴交于点 ,与该抛物线的对称轴交于点 ,现将点 向左平移一个单位到点 ,如果该抛物线与线段 有交点,结合函数的图象,求 的取值范围.
答案
一、选择题
1.C 2.B 3.D 4.C 5.C 6.C 7.D 8.A 9.D 10.C 11.B 12.B 13.D
二、填空题
14.
15. 或
16.
17.
18. 或
三、解答题
19. ;;;;;;,;,
20.
(1) 设租用A型客车为 辆,则租用B型客车为 辆,由题意得 .
(2) 由题意得解得而费用 .
因为 为整数, 取最小时,费用 最低,
所以 ,.
所以方案为租用A型客车 辆,租用B型客车 辆.
21.
(1)
(2)
22.
(1) 把 代入 得:,
,
抛物线的对称轴为 .
(2) 由()可知,抛物线解析式为 ,对称轴为 ,
抛物线过点 ,.
当 时,,
.
当 时,如图.
由该抛物线与线段 有交点可得:当 时,,
即 ,解得:;
当 时,由题意得:,
,如图.
由该抛物线与线段 有交点可得:当 时,,
即 ,解得:.
综上所述, 的取值范围为 或 .
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
