四年级下册数学课件-4.1三角形内角和的探究与运用- 西师大版(共18张PPT)
文档属性
| 名称 | 四年级下册数学课件-4.1三角形内角和的探究与运用- 西师大版(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 855.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 08:08:47 | ||
图片预览




文档简介
(共18张PPT)
三角形内角和的探究与运用
四年级下册第四单元
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天, ∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊!” ∠1说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” ∠2很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
∠1
∠2
∠3
三角形内角和
内角
∠1
∠2
∠3
∠1+∠2+∠3
=180
90o+60o+30o=180o
90o+45o+45o=180o
三角形内角和=180°
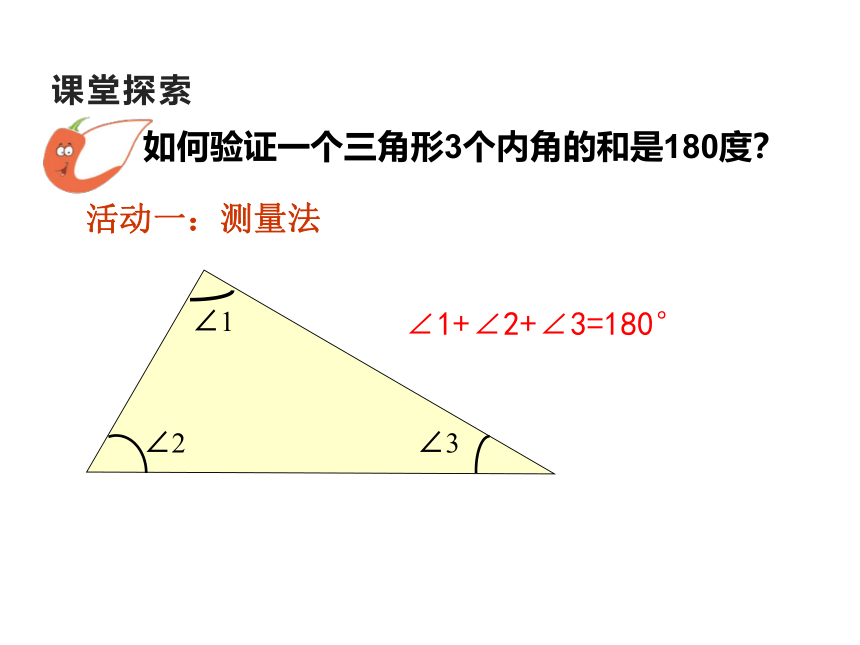
课堂探索
如何验证一个三角形3个内角的和是180度?
∠1+∠2+∠3=180°
活动一:测量法
∠1
∠3
∠2
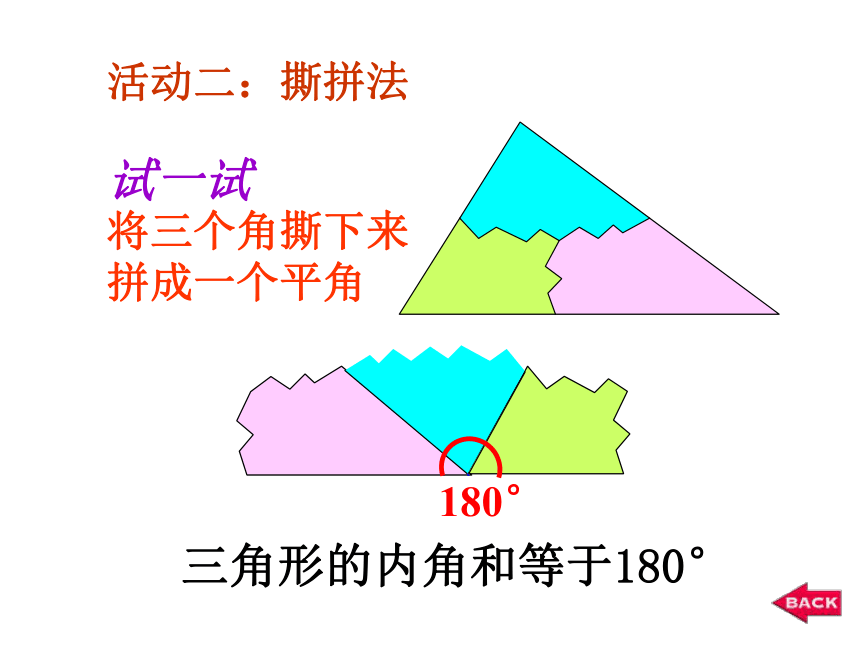
试一试
三角形的内角和等于180°
将三个角撕下来
拼成一个平角
活动二:撕拼法
180°
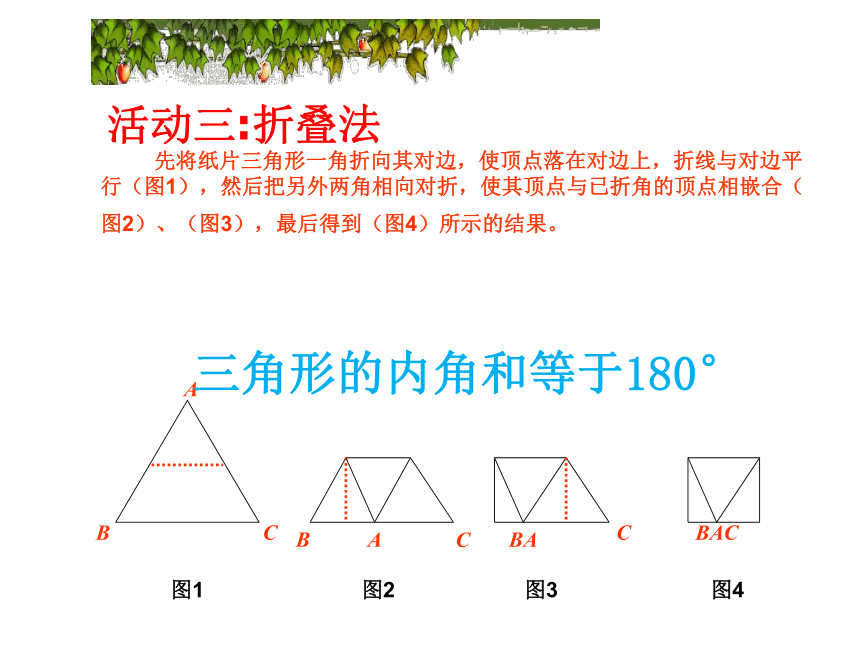
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
活动三:折叠法
三角形的内角和等于180°
课堂探索
用撕拼法,三角形内角和是180°。
测量了几个三角形,三角形内角和是180°。
我用折拼法,三角形内角和也是180 °。
回顾:三角形的内角和是180°
“在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。”
——毕达哥拉斯
课堂练习
只要另两个角的和是( )就可以了。
三角形的一个角是80°,另两个角可能各是多少度?
100
一、如图:∠1=55°,∠2=45°,∠3=?
∠3=180°-55°-45°=80
二、直角三角形中,一个锐角是50°,另一个锐角是多少度?
180°-90°-50°=40°
或 90°-50°=40°
三、一个等腰三角形的顶角是100°,求它的一个底角是多少度?
(180°-100°)÷ 2=40°
四、一个等腰三角形的内角是50°,则另外两个内角分别是多少度?
第一种情况:
底角是50°时,另一个底角也是50°,
顶角是180°-50°×2=80°
第二种情况:
顶角是50°时,两个底角都是:
(180°-50°)÷ 2=65°
五、一个等腰三角形,它的底角的度数是顶角度数的2倍。这个三角形的顶角和一个底角各是多少度?
顶角
底角
底角
180°÷(2+2+1)
=180°÷5
=36°
顶角:36°×1=36°
一个底角:36°×2=72°
六、一个等腰三角形中,已知一个内角是另一个内角的4倍,那么这个三角形的顶角和一个底角各是多少度?
底角是顶角的4倍
顶角是底角的4倍
顶角
底角
底角
180°÷(4+4+1)
=180°÷9
=20°
底角
底角
顶角
180°÷(1+1+4)
=180°÷6
=30°
顶角:20°×1=20°
一个底角:20°×4=80°
一个底角:30°×1=30°
顶角:30°×4=120°
六、一个等腰三角形中,已知一个内角是另一个内角的4倍,那么这个三角形的顶角和一个底角各是多少度?
底角是顶角的4倍
顶角是底角的4倍
顶角
底角
底角
180°÷(4+4+1)
=180°÷9
=20°
底角
底角
顶角
180°÷(1+1+4)
=180°÷6
=30°
顶角:20°×1=20°
一个底角:20°×4=80°
一个底角:30°×1=30°
顶角:30°×4=120°
形状似座山,稳定性能坚,
三竿首尾连,学问不简单。
根据所学的知识,你能想办法求出下列图形的内角和吗?
三角形内角和的探究与运用
四年级下册第四单元
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结。可是有一天, ∠2突然不高兴,发起脾气来,它指着∠1说:“你凭什么度数最大,我也要和你一样大!”“不行啊!” ∠1说:“这是不可能的,否则,我们这个家就再也围不起来了……”“为什么?” ∠2很纳闷。
同学们,你们知道其中的道理吗?
内角三兄弟之争
∠1
∠2
∠3
三角形内角和
内角
∠1
∠2
∠3
∠1+∠2+∠3
=180
90o+60o+30o=180o
90o+45o+45o=180o
三角形内角和=180°
课堂探索
如何验证一个三角形3个内角的和是180度?
∠1+∠2+∠3=180°
活动一:测量法
∠1
∠3
∠2
试一试
三角形的内角和等于180°
将三个角撕下来
拼成一个平角
活动二:撕拼法
180°
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
活动三:折叠法
三角形的内角和等于180°
课堂探索
用撕拼法,三角形内角和是180°。
测量了几个三角形,三角形内角和是180°。
我用折拼法,三角形内角和也是180 °。
回顾:三角形的内角和是180°
“在数学的天地里,重要的不是我们知道什么,而是我们怎么知道的。”
——毕达哥拉斯
课堂练习
只要另两个角的和是( )就可以了。
三角形的一个角是80°,另两个角可能各是多少度?
100
一、如图:∠1=55°,∠2=45°,∠3=?
∠3=180°-55°-45°=80
二、直角三角形中,一个锐角是50°,另一个锐角是多少度?
180°-90°-50°=40°
或 90°-50°=40°
三、一个等腰三角形的顶角是100°,求它的一个底角是多少度?
(180°-100°)÷ 2=40°
四、一个等腰三角形的内角是50°,则另外两个内角分别是多少度?
第一种情况:
底角是50°时,另一个底角也是50°,
顶角是180°-50°×2=80°
第二种情况:
顶角是50°时,两个底角都是:
(180°-50°)÷ 2=65°
五、一个等腰三角形,它的底角的度数是顶角度数的2倍。这个三角形的顶角和一个底角各是多少度?
顶角
底角
底角
180°÷(2+2+1)
=180°÷5
=36°
顶角:36°×1=36°
一个底角:36°×2=72°
六、一个等腰三角形中,已知一个内角是另一个内角的4倍,那么这个三角形的顶角和一个底角各是多少度?
底角是顶角的4倍
顶角是底角的4倍
顶角
底角
底角
180°÷(4+4+1)
=180°÷9
=20°
底角
底角
顶角
180°÷(1+1+4)
=180°÷6
=30°
顶角:20°×1=20°
一个底角:20°×4=80°
一个底角:30°×1=30°
顶角:30°×4=120°
六、一个等腰三角形中,已知一个内角是另一个内角的4倍,那么这个三角形的顶角和一个底角各是多少度?
底角是顶角的4倍
顶角是底角的4倍
顶角
底角
底角
180°÷(4+4+1)
=180°÷9
=20°
底角
底角
顶角
180°÷(1+1+4)
=180°÷6
=30°
顶角:20°×1=20°
一个底角:20°×4=80°
一个底角:30°×1=30°
顶角:30°×4=120°
形状似座山,稳定性能坚,
三竿首尾连,学问不简单。
根据所学的知识,你能想办法求出下列图形的内角和吗?
