2021-2022学年沪科版数学七年级下册6.1平方根、立方根(第2课时立方根)课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年沪科版数学七年级下册6.1平方根、立方根(第2课时立方根)课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 456.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 09:40:51 | ||
图片预览








文档简介
(共21张PPT)
6.1 平方根、立方根
第6章 实数
沪科版数学七年级下
第二课时 立方根
6.求一个数的平方根的运算,叫
如果一个数的平方等于a,那么这个数叫做a的平方根
1. 什么叫平方根
2. 数a的平方根表示为 。
3.一个正数有 平方根,这两个平方根互为 。
4.0的平方根是 。
5.负数 平方根.
两个
相反数
0
没有
知识回顾
开平方
1、一个数的平方根是-7,则它的另一个平方根
是 , 这个数是 .
2、 的平方根是它本身.
3、 .
7
49
0
-0.4
4、 = .
5、 .
9
回顾练习1
填空:
1、64的平方根是8. ( )
2、2的平方根可表示成 .( )
3、(-4)2的算术平方根是-4.( )
判断正误,若错误请说明理由
对
错
错
错
4、 ( )
回顾练习2
说出下列各式的意义,并计算:
回顾练习3
解:
=12
= -0.9
=14
=±
问题:要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:(1)什么数的立方等于-8?
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
设正方体的棱长为X㎝,则
这就是要求一个数,使它的立方等于27.
因为
所以 X=3. 正方体的棱长为3㎝
-2
新知探究
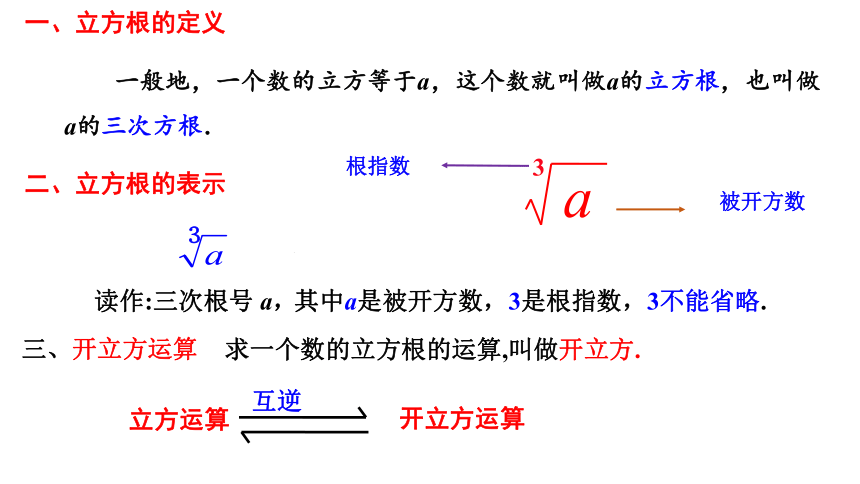
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
3
一、立方根的定义
二、立方根的表示
a
3
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号 a,
新知讲解
三、开立方运算
立方运算
开立方运算
互逆
求一个数的立方根的运算,叫做开立方.
例1、求下列各数的立方根.
(1)
(2)
(3)
解:
(1)∵()3 =
∴
即
(2)∵()3 =
∴-343
即
(3)∵(-0.6)3 =-0.216
∴-0.216
即
例题讲解
根据立方根的意义填空.
因为 23 =8,所以8的立方根是( )
因为( )3 =0.125,所以0.125的立方是( )
因为( )3 =0,所以0的立方根是( )
因为( )3 =-8,所以-8的立方根是( )
因为( )3 =- ,所以- 的立方根是( )
0
2
-2
0
-2
你能看出正数,0,负数的立方根各有什么特点
新知探究
想一想
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
四、立方根的性质
讨论:平方根和立方根的异同点
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
新知探究
= ,
= .
互为相反数的两个数a与-a的立方根的关系
a
3
-a
3
=
-7
-7
=
-8
-8
互为相反数的数的立方根也互为相反数
∴
=
,
=
∴
引伸探究
规律:对于任何数a都有
规律:对于任何数a都有
2
-2
-3
4
0
8
-8
27
-27
0
例2、求下列各式的值.
解:
= -2
= -3
==
==
练一练
1.判断下列说法是否正确,并说明理由
x
(2) 25的平方根是5
x
(3) -64没有立方根
x
(4) -4的平方根是
x
(5) 0的平方根和立方根都是
√
(1)
的立方根是
( )
( )
( )
( )
( )
(1)立方根是它本身的数是 ,
平方根是它本身的数是
1, -1, 0
0
2、填空
练一练
(2) 的平方根是 ,的立方根是
的立方根是 ,
2
-(-1)2的立方根是 ,
(-1)2的平方根是 ,
-1
±1
(4) 的平方根为 .
±2
(5)若一个数的平方根为±8,则这个数的立方根是 。
4
3.你能求出下列各式中的未知数x吗?
(1) x3=729 (2)(x-1)3=125
解:
∴x=9
∴x-1=5
X=6
(3)
(4)
(3)
x=23
(4)
X-2=43
∴X=66
∴x=8
练一练
平方根 立方根
定 义
性 质 正 数
0
负 数
开 方
表 示
如果一个数x 的平方等于a,那么这个数x就叫做a的平方根。
如果一个数x 的立方等于a,那么这个数x就做叫a的立方根。
有两个平方根,互为相反数
0
没有平方根
求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。
,其中a 是被开方数,
根指数2 (省略)
求一个数的立方根的运算叫开
立方;开立方与立方是互逆运算。
有一个负的立方根
0
有一个正的立方根
,其中a 是被开方数,
根指数3 (不能省略)
区别、联系
课堂小结
1.求下列各式的值:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
算术平方根:求一个正数,使它的平方等于被开方数.
平方根:求两个相反数,使它的平方等于被开方数.
立方根:求一个数,使它的立方等于被开方数.
求
提升练习
(1)若x2-9=0,y3+27=0,求x+y的值,
提升练习
2、解下列各题
解:
∵x2-9=0
∴x2=9
∴x = ±
∴x = ±
∵ y3+27=0
∴y3= -27
∴y= =-3
∴ 当x =
x+y=3-3=0
当x = -
x+y=-3-3=0-6
解:
=
已知半径为r 的球,其体积 的计 算公式
为 .如果甲、乙两球 体积
的比为1 :8,则甲、乙两球的半径比为 .
R
r
乙
甲
1 : 2
拓展练习
6.1 平方根、立方根
第6章 实数
沪科版数学七年级下
第二课时 立方根
6.求一个数的平方根的运算,叫
如果一个数的平方等于a,那么这个数叫做a的平方根
1. 什么叫平方根
2. 数a的平方根表示为 。
3.一个正数有 平方根,这两个平方根互为 。
4.0的平方根是 。
5.负数 平方根.
两个
相反数
0
没有
知识回顾
开平方
1、一个数的平方根是-7,则它的另一个平方根
是 , 这个数是 .
2、 的平方根是它本身.
3、 .
7
49
0
-0.4
4、 = .
5、 .
9
回顾练习1
填空:
1、64的平方根是8. ( )
2、2的平方根可表示成 .( )
3、(-4)2的算术平方根是-4.( )
判断正误,若错误请说明理由
对
错
错
错
4、 ( )
回顾练习2
说出下列各式的意义,并计算:
回顾练习3
解:
=12
= -0.9
=14
=±
问题:要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:(1)什么数的立方等于-8?
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?
设正方体的棱长为X㎝,则
这就是要求一个数,使它的立方等于27.
因为
所以 X=3. 正方体的棱长为3㎝
-2
新知探究
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫做a的三次方根.
3
一、立方根的定义
二、立方根的表示
a
3
根指数
被开方数
其中a是被开方数,3是根指数,3不能省略.
读作:三次根号 a,
新知讲解
三、开立方运算
立方运算
开立方运算
互逆
求一个数的立方根的运算,叫做开立方.
例1、求下列各数的立方根.
(1)
(2)
(3)
解:
(1)∵()3 =
∴
即
(2)∵()3 =
∴-343
即
(3)∵(-0.6)3 =-0.216
∴-0.216
即
例题讲解
根据立方根的意义填空.
因为 23 =8,所以8的立方根是( )
因为( )3 =0.125,所以0.125的立方是( )
因为( )3 =0,所以0的立方根是( )
因为( )3 =-8,所以-8的立方根是( )
因为( )3 =- ,所以- 的立方根是( )
0
2
-2
0
-2
你能看出正数,0,负数的立方根各有什么特点
新知探究
想一想
一个正数有一个正的立方根;
一个负数有一个负的立方根,
零的立方根是零。
四、立方根的性质
讨论:平方根和立方根的异同点
被开方数 平方根 立方根
有两个互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
正数
负数
零
新知探究
= ,
= .
互为相反数的两个数a与-a的立方根的关系
a
3
-a
3
=
-7
-7
=
-8
-8
互为相反数的数的立方根也互为相反数
∴
=
,
=
∴
引伸探究
规律:对于任何数a都有
规律:对于任何数a都有
2
-2
-3
4
0
8
-8
27
-27
0
例2、求下列各式的值.
解:
= -2
= -3
==
==
练一练
1.判断下列说法是否正确,并说明理由
x
(2) 25的平方根是5
x
(3) -64没有立方根
x
(4) -4的平方根是
x
(5) 0的平方根和立方根都是
√
(1)
的立方根是
( )
( )
( )
( )
( )
(1)立方根是它本身的数是 ,
平方根是它本身的数是
1, -1, 0
0
2、填空
练一练
(2) 的平方根是 ,的立方根是
的立方根是 ,
2
-(-1)2的立方根是 ,
(-1)2的平方根是 ,
-1
±1
(4) 的平方根为 .
±2
(5)若一个数的平方根为±8,则这个数的立方根是 。
4
3.你能求出下列各式中的未知数x吗?
(1) x3=729 (2)(x-1)3=125
解:
∴x=9
∴x-1=5
X=6
(3)
(4)
(3)
x=23
(4)
X-2=43
∴X=66
∴x=8
练一练
平方根 立方根
定 义
性 质 正 数
0
负 数
开 方
表 示
如果一个数x 的平方等于a,那么这个数x就叫做a的平方根。
如果一个数x 的立方等于a,那么这个数x就做叫a的立方根。
有两个平方根,互为相反数
0
没有平方根
求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。
,其中a 是被开方数,
根指数2 (省略)
求一个数的立方根的运算叫开
立方;开立方与立方是互逆运算。
有一个负的立方根
0
有一个正的立方根
,其中a 是被开方数,
根指数3 (不能省略)
区别、联系
课堂小结
1.求下列各式的值:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
算术平方根:求一个正数,使它的平方等于被开方数.
平方根:求两个相反数,使它的平方等于被开方数.
立方根:求一个数,使它的立方等于被开方数.
求
提升练习
(1)若x2-9=0,y3+27=0,求x+y的值,
提升练习
2、解下列各题
解:
∵x2-9=0
∴x2=9
∴x = ±
∴x = ±
∵ y3+27=0
∴y3= -27
∴y= =-3
∴ 当x =
x+y=3-3=0
当x = -
x+y=-3-3=0-6
解:
=
已知半径为r 的球,其体积 的计 算公式
为 .如果甲、乙两球 体积
的比为1 :8,则甲、乙两球的半径比为 .
R
r
乙
甲
1 : 2
拓展练习
