2021-2022学年华东师大版八年级数学下册第20章数据的整理与初步处理 单元测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学下册第20章数据的整理与初步处理 单元测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 99.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 09:50:24 | ||
图片预览



文档简介
第20章 数据的整理与初步处理 单元测试卷
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 在初中体育中考中,随意抽取某校位同学一分钟跳绳的次数分别为:,,,,,则由这组数据得到的结论错误的是( )
A.平均数为 B.中位数为 C.众数为 D.方差为
2. 某篮球队名场上队员的身高(单位:)是:,,,,.现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员身高的
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
3. 某班抽取名同学参加防震减灾知识竞赛,成绩如下:,,,,,,,.关于这组数据下列表述中错误的是( )
A.众数是 B.平均数是 C.中位数是 D.方差是
4. 小莉读高一的哥哥上学期期考的五科成绩如下表:
科目 语文 数学 英语 物理 化学
成绩
则小莉哥哥五科成绩的平均分是( )
A. B. C. D.
5. 在数据,,,,,,,,中,中位数是( )
A. B. C. D.
6. 七年级同学进行体能测试,一班有个学生,平均成绩分,二班有个学生,平均成绩分,则一、二班所有学生的平均成绩为( )
A. B. C. D.
7. 张明同学是名“气象爱好者”,他记录了今年三月份连续天的最低气温(单位),,,,,,关于这组数据,下列结论不正确的是( )
A.平均数是 B.中位数是 C.众数是 D.方差是
8. 在某校“我的中国梦”演讲比赛中,有名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前名,不仅要了解自己的成绩,还要了解这名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
9. 某次射击比赛中,某运动员次射击成绩(单位:环)分别为:,,,,,,则这些数据的方差为________.
10. 已知一组数据、、、、、的众数为,则这组数据的平均数为________.
11. 小华根据朗诵比赛中位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是________.
12. 甲、乙两人进行飞镖比赛,每人各投次,所得平均环数相等,其中甲所得环数的方差为,乙所得环数如下:,,,,,那么成绩较稳定的是_________.(填“甲”或“乙”)
13. 某企业销售部门有两名经理和名销售员,已知经理的月平均工资为元,销售员的月平均工资为元,则该销售部门的月平均工资为________.
14. 已知:数据,,的平均数为,则数据,,的平均数是________.
15. 已知一组数据,,,,,的中位数为,则其方差为________.
16. 如表是某校女子排球队队员的年龄分布:
年龄
频数
则该校女子排球队队员的平均年龄为________岁.
17. 我市某中学九(1)班为“阳光体育运动”自筹资金购买体育器材,全班名同学筹款情况如下表,则该班同学筹款金额的众数是________元.
筹款金额(元)
人数
三、 解答题 (本题共计 7 小题 ,共计69分 , )
18. 有甲、乙两个箱子,其中甲箱内有颗球,分别标记号码,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出颗球放入乙箱后,乙箱内球的号码的中位数为.若此时甲箱内有颗球的号码小于,有颗球的号码大于,若他们的中位数都为,求的值.
19. 为降低新冠疫情给企业带来的风险,某企业加强了管理,准备采取每天的任务定额和超产有奖的措施,以提高工作效率.下面是该企业名员工过去一天中各自装配机器的数量(单位:台):,,,,,,,,,.
求这组数的平均数、众数和中位数;
管理者为了提高员工的工作效率,又不能挫伤其积极性,应确定每位员工的标准日产量为多少台比较恰当?
20. 某市举行英语口语大赛,现甲、乙两校各人的比赛成绩如下表(分制):
甲校
乙校
甲校成绩的众数是________分,乙校成绩的中位数是________分;
计算甲校的平均成绩和方差;
已知乙校成绩的方差是,则成绩较为整齐的是________校.
21. 某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证元,只限本人当年使用,凭证游泳每次付费元;方式二:不购买会员证,每次游泳付费元.
设小明计划今年夏季游泳次数为(为正整数).
(1)根据题意,填写下表
游泳次数
方式一的总费用/元
方式二的总费用/元
(2)若小明计划今年夏季游泳的总费用为元,则选择哪种付费方式,他游泳的次数比较多?
(3)当,小明选择哪种付费方式更合算?请说明理由.
22. 为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,次打靶命中的环数如右:甲:,,,,; 乙:,,,,.
(1)将下表填写完整:
平 均 数
方 差
甲
________
________
乙
________
(2)若你是教练,根据以上信息,你会选择谁参加射击比赛,理由是什么?
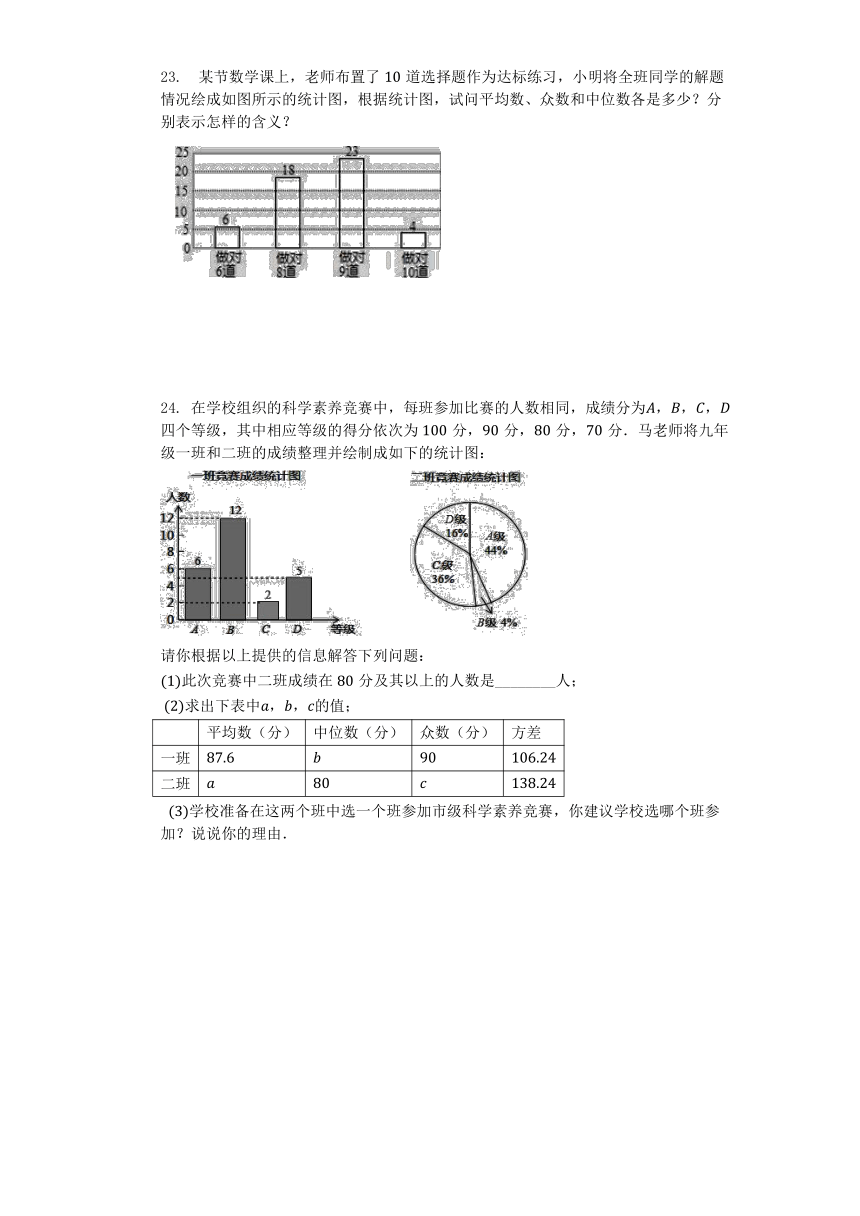
23. 某节数学课上,老师布置了道选择题作为达标练习,小明将全班同学的解题情况绘成如图所示的统计图,根据统计图,试问平均数、众数和中位数各是多少?分别表示怎样的含义?
24. 在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为,,,四个等级,其中相应等级的得分依次为分,分,分,分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
此次竞赛中二班成绩在分及其以上的人数是________人;
求出下表中,,的值;
平均数(分) 中位数(分) 众数(分) 方差
一班
二班
学校准备在这两个班中选一个班参加市级科学素养竞赛,你建议学校选哪个班参加?说说你的理由.
参考答案
第20章 数据的整理与初步处理 单元测试卷
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.D
2.C
3.C
4.C
5.C
6.C
7.D
8.B
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
9.
10.
11.中位数
12.甲
13.元
14.
15.
16.
17.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
18.
【答案】
解:因为他们的中位数都为,所以甲、乙箱内球的数量应该都是偶数,
设在甲箱内球的号码小于的数量是颗,则大于的数量也是颗;
设在乙箱内球的号码小于数量是颗,则大于数量也是颗,
于是在全部颗球中,号码小于数量是颗,大于数量也是颗,即的中位数是,
∴ .
19.
【答案】
解:平均数为:
.
因为这组数据中装配台的最多,
所以众数为.
将这组数据按照从小到大排列为:
,,,,,,,,,,
所以中位数为.
应确定每位员工的标准日产量为台比较恰当.
因为:若规定台,则大多数工人不需要努力就可以完成任务,不利于促进生产.
比较合理的标准日产量应该确定在恰好能使多数人有超过的能力,因此取中位数台比较恰当.
20.
【答案】
,
甲校的平均成绩是:,
则方差是:.
乙
21.
【答案】
解:(1)填表如下:
游泳次数
方式一的总费用/元
方式二的总费用/元
(2)令,解得;
令,解得,
因为,
故小明选择方式一时,游泳的次数比较多.
(3)令,解得;
令,解得;
令,解得,
故当时,小明选择方式二更合算;当时,小明选择方式一,方式二所需费用一样;当时,小明选择方式一更合算.
22.
【答案】
解:,,
解:选择甲参加射击比赛,原因是甲乙两人的平均数一样,甲的方差比较小,根据方差越小越稳定,因此甲比较稳定,所以选择甲
23.
【答案】
平均数,表示该班同学平均每人作对道题多一点;中位数为,是这组数据排序后第和个数据的平均数;众数为,表示
作对道题的人数最多.
24.
【答案】
由一班竞赛成绩统计图可知,
,
二班参加的总人数和一班一样多,
二班参加的人数是:,
,
,
即,,;
选择一班参加,
理由:由表格可知,两个班的平均数相同,
但一班的中位数高于二班,并且一班的方差小于二班,
学生成绩发挥比较稳定,
故选择一班.试卷第1页,总1页
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 , )
1. 在初中体育中考中,随意抽取某校位同学一分钟跳绳的次数分别为:,,,,,则由这组数据得到的结论错误的是( )
A.平均数为 B.中位数为 C.众数为 D.方差为
2. 某篮球队名场上队员的身高(单位:)是:,,,,.现用一名身高为的队员换下场上身高为的队员,与换人前相比,场上队员身高的
A.平均数变小,方差变小
B.平均数变小,方差变大
C.平均数变大,方差变小
D.平均数变大,方差变大
3. 某班抽取名同学参加防震减灾知识竞赛,成绩如下:,,,,,,,.关于这组数据下列表述中错误的是( )
A.众数是 B.平均数是 C.中位数是 D.方差是
4. 小莉读高一的哥哥上学期期考的五科成绩如下表:
科目 语文 数学 英语 物理 化学
成绩
则小莉哥哥五科成绩的平均分是( )
A. B. C. D.
5. 在数据,,,,,,,,中,中位数是( )
A. B. C. D.
6. 七年级同学进行体能测试,一班有个学生,平均成绩分,二班有个学生,平均成绩分,则一、二班所有学生的平均成绩为( )
A. B. C. D.
7. 张明同学是名“气象爱好者”,他记录了今年三月份连续天的最低气温(单位),,,,,,关于这组数据,下列结论不正确的是( )
A.平均数是 B.中位数是 C.众数是 D.方差是
8. 在某校“我的中国梦”演讲比赛中,有名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前名,不仅要了解自己的成绩,还要了解这名学生成绩的( )
A.众数 B.中位数 C.平均数 D.方差
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
9. 某次射击比赛中,某运动员次射击成绩(单位:环)分别为:,,,,,,则这些数据的方差为________.
10. 已知一组数据、、、、、的众数为,则这组数据的平均数为________.
11. 小华根据朗诵比赛中位评委所给的分数作了如下表格:
平均数
中位数
众数
方差
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是________.
12. 甲、乙两人进行飞镖比赛,每人各投次,所得平均环数相等,其中甲所得环数的方差为,乙所得环数如下:,,,,,那么成绩较稳定的是_________.(填“甲”或“乙”)
13. 某企业销售部门有两名经理和名销售员,已知经理的月平均工资为元,销售员的月平均工资为元,则该销售部门的月平均工资为________.
14. 已知:数据,,的平均数为,则数据,,的平均数是________.
15. 已知一组数据,,,,,的中位数为,则其方差为________.
16. 如表是某校女子排球队队员的年龄分布:
年龄
频数
则该校女子排球队队员的平均年龄为________岁.
17. 我市某中学九(1)班为“阳光体育运动”自筹资金购买体育器材,全班名同学筹款情况如下表,则该班同学筹款金额的众数是________元.
筹款金额(元)
人数
三、 解答题 (本题共计 7 小题 ,共计69分 , )
18. 有甲、乙两个箱子,其中甲箱内有颗球,分别标记号码,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出颗球放入乙箱后,乙箱内球的号码的中位数为.若此时甲箱内有颗球的号码小于,有颗球的号码大于,若他们的中位数都为,求的值.
19. 为降低新冠疫情给企业带来的风险,某企业加强了管理,准备采取每天的任务定额和超产有奖的措施,以提高工作效率.下面是该企业名员工过去一天中各自装配机器的数量(单位:台):,,,,,,,,,.
求这组数的平均数、众数和中位数;
管理者为了提高员工的工作效率,又不能挫伤其积极性,应确定每位员工的标准日产量为多少台比较恰当?
20. 某市举行英语口语大赛,现甲、乙两校各人的比赛成绩如下表(分制):
甲校
乙校
甲校成绩的众数是________分,乙校成绩的中位数是________分;
计算甲校的平均成绩和方差;
已知乙校成绩的方差是,则成绩较为整齐的是________校.
21. 某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证元,只限本人当年使用,凭证游泳每次付费元;方式二:不购买会员证,每次游泳付费元.
设小明计划今年夏季游泳次数为(为正整数).
(1)根据题意,填写下表
游泳次数
方式一的总费用/元
方式二的总费用/元
(2)若小明计划今年夏季游泳的总费用为元,则选择哪种付费方式,他游泳的次数比较多?
(3)当,小明选择哪种付费方式更合算?请说明理由.
22. 为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,次打靶命中的环数如右:甲:,,,,; 乙:,,,,.
(1)将下表填写完整:
平 均 数
方 差
甲
________
________
乙
________
(2)若你是教练,根据以上信息,你会选择谁参加射击比赛,理由是什么?
23. 某节数学课上,老师布置了道选择题作为达标练习,小明将全班同学的解题情况绘成如图所示的统计图,根据统计图,试问平均数、众数和中位数各是多少?分别表示怎样的含义?
24. 在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为,,,四个等级,其中相应等级的得分依次为分,分,分,分.马老师将九年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
此次竞赛中二班成绩在分及其以上的人数是________人;
求出下表中,,的值;
平均数(分) 中位数(分) 众数(分) 方差
一班
二班
学校准备在这两个班中选一个班参加市级科学素养竞赛,你建议学校选哪个班参加?说说你的理由.
参考答案
第20章 数据的整理与初步处理 单元测试卷
一、 选择题 (本题共计 8 小题 ,每题 3 分 ,共计24分 )
1.D
2.C
3.C
4.C
5.C
6.C
7.D
8.B
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
9.
10.
11.中位数
12.甲
13.元
14.
15.
16.
17.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
18.
【答案】
解:因为他们的中位数都为,所以甲、乙箱内球的数量应该都是偶数,
设在甲箱内球的号码小于的数量是颗,则大于的数量也是颗;
设在乙箱内球的号码小于数量是颗,则大于数量也是颗,
于是在全部颗球中,号码小于数量是颗,大于数量也是颗,即的中位数是,
∴ .
19.
【答案】
解:平均数为:
.
因为这组数据中装配台的最多,
所以众数为.
将这组数据按照从小到大排列为:
,,,,,,,,,,
所以中位数为.
应确定每位员工的标准日产量为台比较恰当.
因为:若规定台,则大多数工人不需要努力就可以完成任务,不利于促进生产.
比较合理的标准日产量应该确定在恰好能使多数人有超过的能力,因此取中位数台比较恰当.
20.
【答案】
,
甲校的平均成绩是:,
则方差是:.
乙
21.
【答案】
解:(1)填表如下:
游泳次数
方式一的总费用/元
方式二的总费用/元
(2)令,解得;
令,解得,
因为,
故小明选择方式一时,游泳的次数比较多.
(3)令,解得;
令,解得;
令,解得,
故当时,小明选择方式二更合算;当时,小明选择方式一,方式二所需费用一样;当时,小明选择方式一更合算.
22.
【答案】
解:,,
解:选择甲参加射击比赛,原因是甲乙两人的平均数一样,甲的方差比较小,根据方差越小越稳定,因此甲比较稳定,所以选择甲
23.
【答案】
平均数,表示该班同学平均每人作对道题多一点;中位数为,是这组数据排序后第和个数据的平均数;众数为,表示
作对道题的人数最多.
24.
【答案】
由一班竞赛成绩统计图可知,
,
二班参加的总人数和一班一样多,
二班参加的人数是:,
,
,
即,,;
选择一班参加,
理由:由表格可知,两个班的平均数相同,
但一班的中位数高于二班,并且一班的方差小于二班,
学生成绩发挥比较稳定,
故选择一班.试卷第1页,总1页
