2021-2022学年人教版九年级上册及九年级下第26章、第27章数学知识检测试卷(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级上册及九年级下第26章、第27章数学知识检测试卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 671.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 09:53:44 | ||
图片预览

文档简介
2021-2022学年度九年级数学知识滚动检测试卷
(包含内容:九年级上册及九年级下第26章、第27章)
一、单项选择题(每题3分,共30分)
1.将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )
A.y=x2﹣8x+22 B.y=x2﹣8x+14 C.y=x2+4x+10 D.y=x2+4x+2
2.如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按顺时针方向旋转90°后,得到△A′B′C′,则点A'的坐标是( )
A.(﹣5,1) B.(5,﹣1) C.(﹣1,5) D.(1,﹣5)
3.已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C.且 D.且
4.下列事件中是必然事件的是( )
A.抛掷一枚质地均匀的硬币,正面朝上 B.随意翻到一本书的某页,这一页的页码是偶数
C.打开电视机,正在播放广告 D.从两个班级中任选三名学生,至少有两名学生来自同一个班级
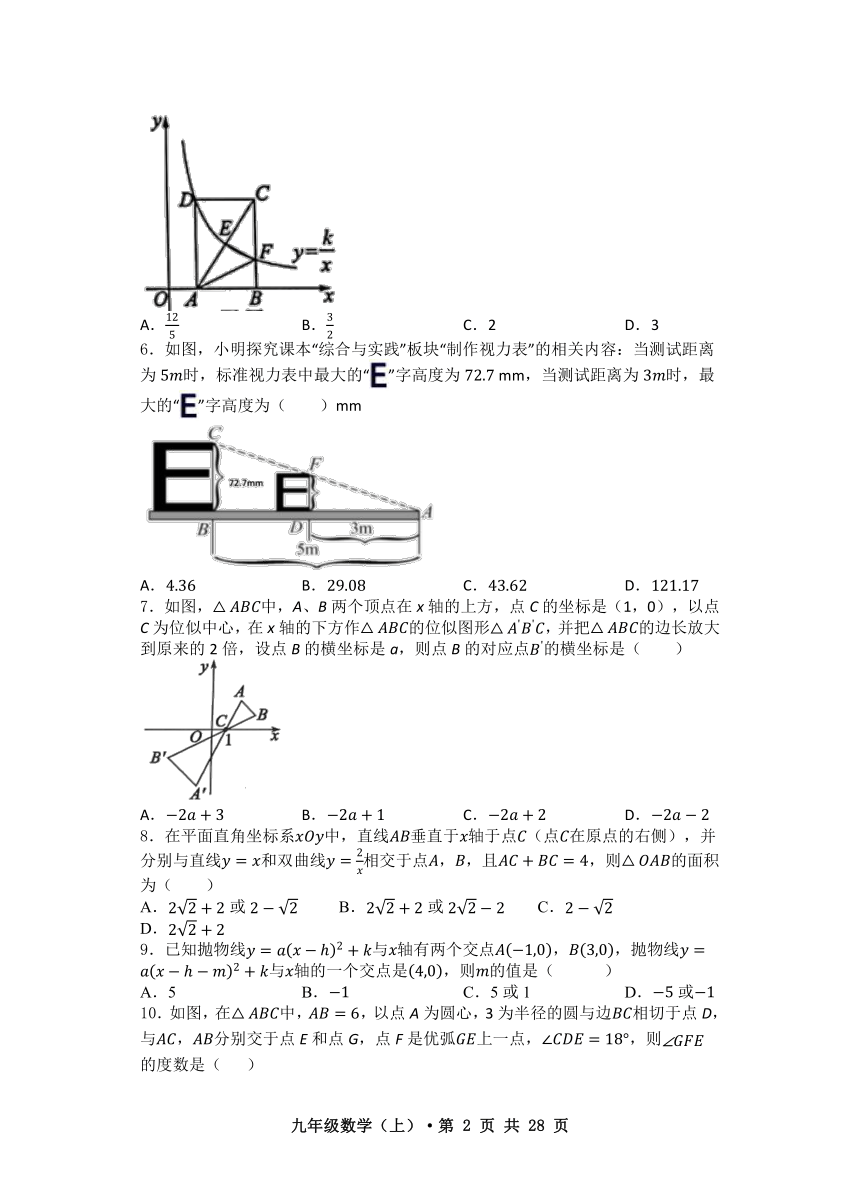
5.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
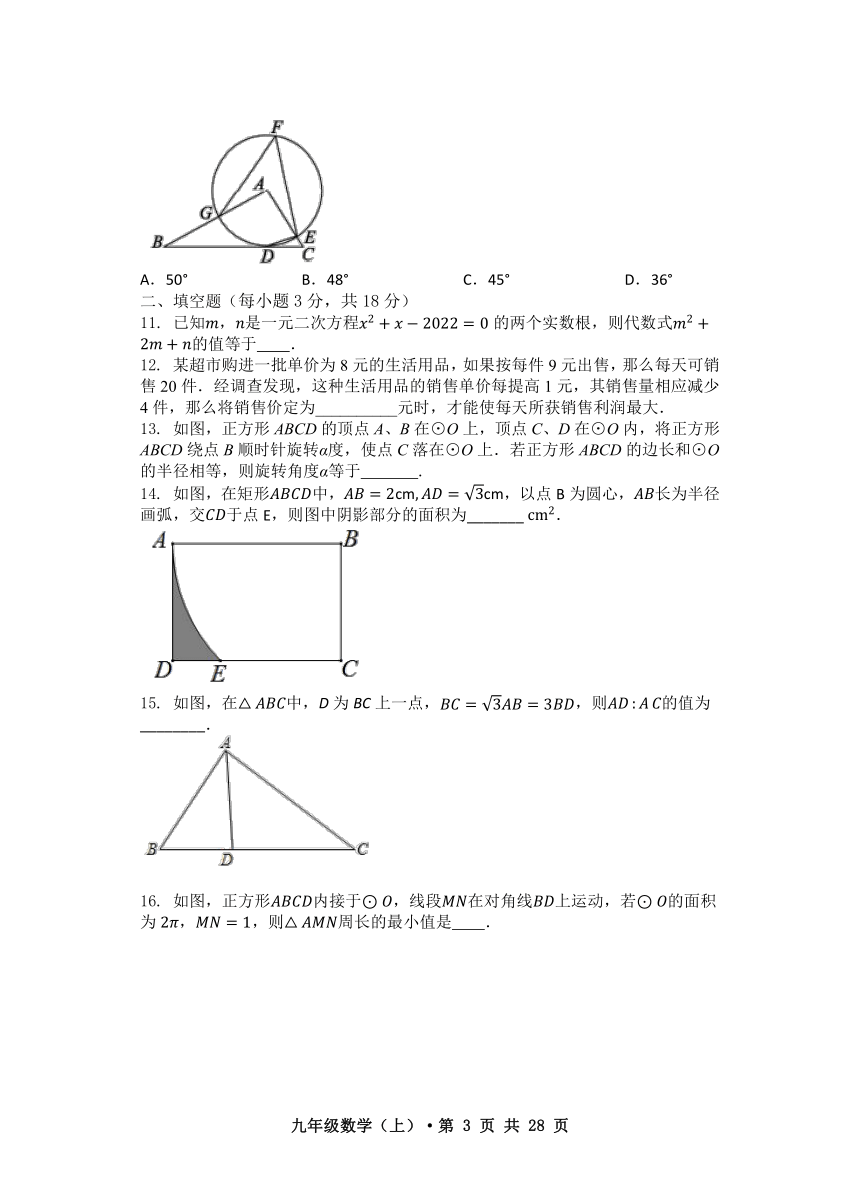
6.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为 mm,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
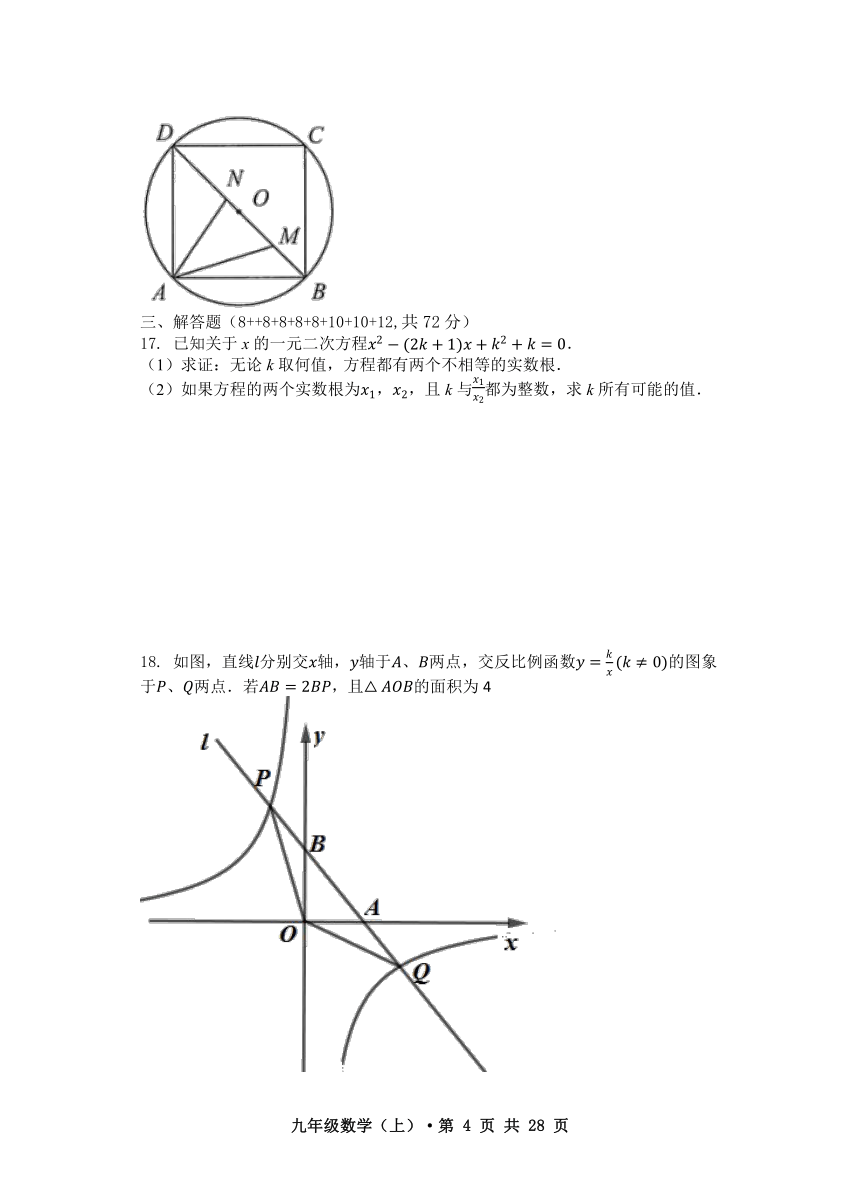
7.如图,中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A. B. C. D.
8.在平面直角坐标系中,直线垂直于轴于点(点在原点的右侧),并分别与直线和双曲线相交于点,,且,则的面积为( )
A.或 B.或 C. D.
9.已知抛物线与轴有两个交点,,抛物线与轴的一个交点是,则的值是( )
A.5 B. C.5或1 D.或
10.如图,在中,,以点A为圆心,3为半径的圆与边相切于点D,与,分别交于点E和点G,点F是优弧上一点,,则的度数是( )
A.50° B.48° C.45° D.36°
二、填空题(每小题3分,共18分)
11. 已知,是一元二次方程的两个实数根,则代数式的值等于 .
12. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
13. 如图,正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于 .
14. 如图,在矩形中,,以点B为圆心,长为半径画弧,交于点E,则图中阴影部分的面积为_______.
15. 如图,在中,D为BC上一点,,则的值为________.
16. 如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是 .
三、解答题(8++8+8+8+8+10+10+12,共72分)
17. 已知关于x的一元二次方程.
(1)求证:无论k取何值,方程都有两个不相等的实数根.
(2)如果方程的两个实数根为,,且k与都为整数,求k所有可能的值.
18. 如图,直线分别交轴,轴于、两点,交反比例函数的图象于、两点.若,且的面积为4
(1)求的值;
(2)当点的横坐标为时,求的面积.
19. 如图,在菱形中,点M,N分别是边,上的点,,.连接,,延长交线段延长线于点E.
(1)求证:;
(2)若,则的长是__________.
20. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
月平均用水量(吨) 3 4 5 6 7
频数(户数) 4 9 10 7
频率 0.08 0.40 0.14
请根据统计表中提供的信息解答下列问题:
(1)填空:______,______,______.
(2)这些家庭中月平均用水量数据的平均数是______,众数是______,中位数是______.
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙丙丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
21. 如图1,在中,,,D为内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.
(1)求证:,;
(2)如图2.连接AF,DC,已知,判断AF与DC的位置关系,并说明理由.
22. 如图,在菱形中,是对角线上一点(),,垂足为,以为半径的分别交于点,交的延长线于点,与交于点.
(1)求证:是的切线;
(2)若是的中点,,.
①求的长;
②求的长.
23. 某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
24. 图1,二次函数的图象交坐标轴于点,,点为轴上一动点.
(1)求二次函数的表达式;
(2)过点作轴分别交线段,抛物线于点,,连接.当时,求的面积;
(3)如图2,将线段绕点逆时针旋转90得到线段.
①当点在抛物线上时,求点的坐标;
②点在抛物线上,连接,当平分时,直接写出点P的坐标.
答案:
一、单项选择题(每题3分,共30分)
1.将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )
A.y=x2﹣8x+22 B.y=x2﹣8x+14 C.y=x2+4x+10 D.y=x2+4x+2
【答案】D
2.如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按顺时针方向旋转90°后,得到△A′B′C′,则点A'的坐标是( )
A.(﹣5,1) B.(5,﹣1) C.(﹣1,5) D.(1,﹣5)
【答案】A
3.已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C.且 D.且
【答案】D
4.下列事件中是必然事件的是( )
A.抛掷一枚质地均匀的硬币,正面朝上 B.随意翻到一本书的某页,这一页的页码是偶数
C.打开电视机,正在播放广告 D.从两个班级中任选三名学生,至少有两名学生来自同一个班级
【答案】D
5.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
【答案】D
6.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为mm,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
【答案】C
7.如图,中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A. B. C. D.
【答案】A
解:设点的横坐标为,
则、间的横坐标的差为,、间的横坐标的差为,
放大到原来的倍得到,
,
解得:.
8.在平面直角坐标系中,直线垂直于轴于点(点在原点的右侧),并分别与直线和双曲线相交于点,,且,则的面积为( )
A.或 B.或 C. D.
【答案】B
解:设点的坐标为,则,
,
,
,
解得或,
经检验,或均为所列方程的根,
(1)当时,,
则的面积为;
(2)当时,,
则的面积为;
综上,的面积为或,
9.已知抛物线与轴有两个交点,,抛物线与轴的一个交点是,则的值是( )
A.5 B. C.5或1 D.或
【答案】C
解:比较抛物线与抛物线,
发现:将前一个抛物线往右平移m个单位后可以得到后一个抛物线的解析式,
∵,与轴的一个交点是,与轴有两个交点,,
∴当前一个抛物线往右平移1个单位时,后一个抛物线与轴的一个交点是,故m=1,
当前一个抛物线往右平移5个单位时,后一个抛物线与轴的一个交点是,故m=5,
10.如图,在中,,以点A为圆心,3为半径的圆与边相切于点D,与,分别交于点E和点G,点F是优弧上一点,,则的度数是( )
A.50° B.48° C.45° D.36°
【答案】B
解:连接AD,则AD=AG=3,
∵BC与圆A相切于点D,
∴∠ADB=∠ADC=90°,
在Rt△ADB中,AB=6,则cos∠BAD==,
∴∠BAD=60°,
∵∠CDE=18°,
∴∠ADE=90°﹣18°=72°,
∵AD=AE,
∴∠ADE=∠AED=72°,
∴∠DAE=180°﹣2×72°=36°,
∴∠GAC=36°+60°=96°,
∴∠GFE=∠GAC=48°,
故选:B.
二、填空题(每小题3分,共18分)
11. 已知,是一元二次方程的两个实数根,则代数式的值等于 .
答案:2021
根据一元二次方程根的定义得到,则,再利用根与系数的关系得到,然后利用整体代入的方法计算.
12. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
【答案】11
解:设销售单价定为元,每天所获利润为元,
则
,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
13. 如图,正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于 .
【答案】α=30°
解:如图所示,连接OA,OB,OG,
由旋转的性质可得,AB=BG,∠ABE=∠CBG=α
∵正方形ABCD的边长和⊙O的半径相等,
∴OA=OB=OG=BG=AB,
∴△OAB和△OBG都是等边三角形,
∴∠OBA=∠OBG=60°,
∵∠ABO+∠OBG=∠ABC+∠CBG=120°,∠ABC=90°(正方形的性质),
∴∠CBG=30°,
∴α=30°,
14. 如图,在矩形中,,以点B为圆心,长为半径画弧,交于点E,则图中阴影部分的面积为_______.
【答案】
解:连接BE,如图所示:
由题意得BE=AB=2cm,
∵四边形ABCD是矩形,
∴,
∵,
∴,
∴∠EBC=30°,∠ABE=60°,
∴,
∴;
故答案为.
15. 如图,在中,D为BC上一点,,则的值为________.
【答案】.
16. 如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是 .
【答案】4
如图所示,
(1)为上一动点,点关于线段的对称点为点,连接,则,过点作的平行线,过点作的平行线,两平行线相交于点,与相交于点M.
四边形是平行四边形
则
(2)找一点, 连接,则,过点作的平行线,连接则.
此时
(1)中周长取到最小值
四边形是平行四边形
四边形是正方形
,
又,,
又
是等腰三角形
,则圆的半径,
三、解答题(8++8+8+8+8+10+10+12,共72分)
17. 已知关于x的一元二次方程.
(1)求证:无论k取何值,方程都有两个不相等的实数根.
(2)如果方程的两个实数根为,,且k与都为整数,求k所有可能的值.
【答案】(1)见解析;(2)0或-2或1或-1
【分析】
(1)计算判别式的值,然后根据判别式的意义得到结论;
(2)先利用因式分解法得出方程的两个根,再结合k与都为整数,得出k的值;
【详解】
解:(1)
∵△=
=
∴无论k取何值, 方程都有两个不相等的实数根.
(2)∵
∴
∴=0
∴,或,
当,时,
∵k与都为整数,
∴k=0或-2
当,时,
∴,
∵k与都为整数,
∴k=1或-1
∴k所有可能的值为0或-2或1或-1
18. 如图,直线分别交轴,轴于、两点,交反比例函数的图象于、两点.若,且的面积为4
(1)求的值;
(2)当点的横坐标为时,求的面积.
【答案】(1)-6;(2)8
解:(1)过作垂直于轴,垂足为,
∴,
∴.
∵,,
∴,,
∴,.
∴,,即.
(2)由(1)知,∴.
∵,∴,∴,.
设直线的解析式为,
将点、代入,得.
解得.
∴直线的解析式为.
联立方程组,解得,,
∴.
∴.
19. 如图,在菱形中,点M,N分别是边,上的点,,.连接,,延长交线段延长线于点E.
(1)求证:;
(2)若,则的长是__________.
【答案】(1)见解析;(2).
【分析】
(1)根据菱形的性质可得,,根据,,可得,利用即可证明;
(2)根据菱形的性质可证明,根据相似的性质可求得的长度,进而可求.
【解析】
解:(1)证明:四边形为菱形,
,,
,,
,
在和中,
,
,
(2)四边形为菱形,
,
,
,
,
,
,
,
,
,
,
,
.
20. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
月平均用水量(吨) 3 4 5 6 7
频数(户数) 4 9 10 7
频率 0.08 0.40 0.14
请根据统计表中提供的信息解答下列问题:
(1)填空:______,______,______.
(2)这些家庭中月平均用水量数据的平均数是______,众数是______,中位数是______.
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙丙丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
【答案】(1)20;0.18;0.20;(2)4.92,4,5;(3)132户;(4),所有等可能结果为(甲,乙)、(甲,丙)、(甲,丁)、(乙,甲)、(乙,丙)、(乙,丁)、(丙,甲)、(丙,乙)、(丙,丁)、(丁,甲)、(丁,乙)(丁,丙)
解:(1)根据题意,被调查样本数为:
∴,,
故答案为:20;0.18;0.20;
(2)平均数是 ,
∵用水量为4吨的共20户,数量最多,
∴众数是4,
∵用水量共50组数据,中间的两个数均为5,
∴中位数是5
故答案为:4.92,4,5;
(3)∵,
∴(户)
∴月平均用水量不超过5吨的约有132户;
(4)画出树状图:
由树状图可以看出,所有可能出现的结果共有12种,即:(甲,乙)、(甲,丙)、(甲,丁)、(乙,甲)、(乙,丙)、(乙,丁)、(丙,甲)、(丙,乙)、(丙,丁)、(丁,甲)、(丁,乙)(丁,丙),这些结果出现的可能性相等.
其中恰好选到甲、丙两户的有2种.
∴(恰好选到甲、丙两户).
21. 如图1,在中,,,D为内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.
(1)求证:,;
(2)如图2.连接AF,DC,已知,判断AF与DC的位置关系,并说明理由.
【答案】(1)见解析;(2),理由见解析
解(1)由旋转的性质,可得∠DAE=90°,AD=AE,
∵∠BAD+∠DAC=∠BAC=90°,∠CAE+∠DAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵
∴,即
∴
∴
∴,即;
(2),理由如下:
∵
∴
由(1)知,
∴A,D,F,E在以DE为直径的圆上,如图,
∵AD=AE
∴弧AD=弧AE,
∴
∴
∴;
22. 如图,在菱形中,是对角线上一点(),,垂足为,以为半径的分别交于点,交的延长线于点,与交于点.
(1)求证:是的切线;
(2)若是的中点,,.
①求的长;
②求的长.
【答案】(1)见解析;(2)①;②
(1)证明:如图,过点作于点,
∵是菱形的对角线,
∴,
∵,,
∴∠OEB=∠OMB=90 ,
∵OB=OB,
∴△OEB≌△OMB(AAS)
∴,
∴是的切线.
(2)解:①如图,
∵是的中点,,
∴.
∵,,
∴,
∴,
∴在Rt△OGH中,
∴∠GHO=30°,∠GOH=60°,
∴∠HOE=120°,
∵,∴,
∴由弧长公式,得到的长:.
②方法一:如图,过点作于点,
∵,
∴,
∴,
∴,
∵DG//NE,DN//GE,∠GEN=90
∴四边形NEGD是矩形,
∴NE=DG=1,BN=3,OE=4,DN=6,
在菱形中,AD=AB,在中,设,
∴,
∴.
方法二:如图,过作于点,
∵,,OE=OH=4,
∴,,,
∴,
∴.
23. 某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
【答案】(1)①,;②10台;(2)分配产销A型车床9台、B型车床5台;或产销A型车床8台、B型车床6台,此时可获得总利润最大值170万元
解:(1)当时,每台就要比17万元少()万元
所以每台获利,也就是()万元
①补全表格如下面:
A型 B型
车床数量/台
每台车床获利/万元 10
②此时,由A型获得的利润是10()万元,
由B型可获得利润为万元,
根据题意:, ,
,∵0≤≤14, ∴,
即应产销B型车床10台;
(2)当0≤≤4时,
当0≤≤4 A型 B型
车床数量/台
每台车床获利/万元 10 17
利润
此时,W=+=,
该函数值随着的增大而增大,当取最大值4时,W最大1=168(万元);
当4<≤14时,
当4<≤14 A型 B型
车床数量/台
每台车床获利/万元 10
利润
则W=+==,
当或时(均满足条件4<≤14),W达最大值W最大2=170(万元),
∵W最大2> W最大1,
∴应分配产销A型车床9台、B型车床5台;或产销A型车床8台、B型车床6台,此时可获得总利润最大值170万元.
24. 图1,二次函数的图象交坐标轴于点,,点为轴上一动点.
(1)求二次函数的表达式;
(2)过点作轴分别交线段,抛物线于点,,连接.当时,求的面积;
(3)如图2,将线段绕点逆时针旋转90得到线段.
①当点在抛物线上时,求点的坐标;
②点在抛物线上,连接,当平分时,直接写出点P的坐标.
【答案】(1);(2);(3)①或;②或.
解:(1)二次函数的图象经过
解得
(2)由,令
解得
当时,
,则
;
(3)如图,当点在轴下方时,过点作于点,
由,令,
解得
,
,
将线段绕点逆时针旋转90得到线段,
,,
设,
点在抛物线上,
解得(舍)
当点在轴上方时,如图,
过点作于点,设
同理可得
点在抛物线上,
解得(舍去),
综上所述,或;
②当不平行于轴时,过点作交于点,过点作于点,如图,
平分,,
,
,
,
当不平行于轴时,重合,
,
当轴时,如图,
此时
则
综上所述,当平方时,点的坐标为或.
九年级数学(上)·第 1 页 共 3 页
(包含内容:九年级上册及九年级下第26章、第27章)
一、单项选择题(每题3分,共30分)
1.将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )
A.y=x2﹣8x+22 B.y=x2﹣8x+14 C.y=x2+4x+10 D.y=x2+4x+2
2.如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按顺时针方向旋转90°后,得到△A′B′C′,则点A'的坐标是( )
A.(﹣5,1) B.(5,﹣1) C.(﹣1,5) D.(1,﹣5)
3.已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C.且 D.且
4.下列事件中是必然事件的是( )
A.抛掷一枚质地均匀的硬币,正面朝上 B.随意翻到一本书的某页,这一页的页码是偶数
C.打开电视机,正在播放广告 D.从两个班级中任选三名学生,至少有两名学生来自同一个班级
5.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
6.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为 mm,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
7.如图,中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A. B. C. D.
8.在平面直角坐标系中,直线垂直于轴于点(点在原点的右侧),并分别与直线和双曲线相交于点,,且,则的面积为( )
A.或 B.或 C. D.
9.已知抛物线与轴有两个交点,,抛物线与轴的一个交点是,则的值是( )
A.5 B. C.5或1 D.或
10.如图,在中,,以点A为圆心,3为半径的圆与边相切于点D,与,分别交于点E和点G,点F是优弧上一点,,则的度数是( )
A.50° B.48° C.45° D.36°
二、填空题(每小题3分,共18分)
11. 已知,是一元二次方程的两个实数根,则代数式的值等于 .
12. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
13. 如图,正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于 .
14. 如图,在矩形中,,以点B为圆心,长为半径画弧,交于点E,则图中阴影部分的面积为_______.
15. 如图,在中,D为BC上一点,,则的值为________.
16. 如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是 .
三、解答题(8++8+8+8+8+10+10+12,共72分)
17. 已知关于x的一元二次方程.
(1)求证:无论k取何值,方程都有两个不相等的实数根.
(2)如果方程的两个实数根为,,且k与都为整数,求k所有可能的值.
18. 如图,直线分别交轴,轴于、两点,交反比例函数的图象于、两点.若,且的面积为4
(1)求的值;
(2)当点的横坐标为时,求的面积.
19. 如图,在菱形中,点M,N分别是边,上的点,,.连接,,延长交线段延长线于点E.
(1)求证:;
(2)若,则的长是__________.
20. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
月平均用水量(吨) 3 4 5 6 7
频数(户数) 4 9 10 7
频率 0.08 0.40 0.14
请根据统计表中提供的信息解答下列问题:
(1)填空:______,______,______.
(2)这些家庭中月平均用水量数据的平均数是______,众数是______,中位数是______.
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙丙丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
21. 如图1,在中,,,D为内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.
(1)求证:,;
(2)如图2.连接AF,DC,已知,判断AF与DC的位置关系,并说明理由.
22. 如图,在菱形中,是对角线上一点(),,垂足为,以为半径的分别交于点,交的延长线于点,与交于点.
(1)求证:是的切线;
(2)若是的中点,,.
①求的长;
②求的长.
23. 某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
24. 图1,二次函数的图象交坐标轴于点,,点为轴上一动点.
(1)求二次函数的表达式;
(2)过点作轴分别交线段,抛物线于点,,连接.当时,求的面积;
(3)如图2,将线段绕点逆时针旋转90得到线段.
①当点在抛物线上时,求点的坐标;
②点在抛物线上,连接,当平分时,直接写出点P的坐标.
答案:
一、单项选择题(每题3分,共30分)
1.将抛物线y=(x﹣1)2+2向左平移3个单位长度,再向下平移4个单位长度所得到的抛物线的解析式为( )
A.y=x2﹣8x+22 B.y=x2﹣8x+14 C.y=x2+4x+10 D.y=x2+4x+2
【答案】D
2.如图,把直角坐标系xOy放置在边长为1的正方形网格中,O是坐标原点,点A、B、C均在格点上,将△ABC绕O点按顺时针方向旋转90°后,得到△A′B′C′,则点A'的坐标是( )
A.(﹣5,1) B.(5,﹣1) C.(﹣1,5) D.(1,﹣5)
【答案】A
3.已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是( )
A. B. C.且 D.且
【答案】D
4.下列事件中是必然事件的是( )
A.抛掷一枚质地均匀的硬币,正面朝上 B.随意翻到一本书的某页,这一页的页码是偶数
C.打开电视机,正在播放广告 D.从两个班级中任选三名学生,至少有两名学生来自同一个班级
【答案】D
5.如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,的面积为1,则k的值为( )
A. B. C.2 D.3
【答案】D
6.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为时,标准视力表中最大的“”字高度为mm,当测试距离为时,最大的“”字高度为( )mm
A. B. C. D.
【答案】C
7.如图,中,A、B两个顶点在x轴的上方,点C的坐标是(1,0),以点C为位似中心,在x轴的下方作的位似图形,并把的边长放大到原来的2倍,设点B的横坐标是a,则点B的对应点的横坐标是( )
A. B. C. D.
【答案】A
解:设点的横坐标为,
则、间的横坐标的差为,、间的横坐标的差为,
放大到原来的倍得到,
,
解得:.
8.在平面直角坐标系中,直线垂直于轴于点(点在原点的右侧),并分别与直线和双曲线相交于点,,且,则的面积为( )
A.或 B.或 C. D.
【答案】B
解:设点的坐标为,则,
,
,
,
解得或,
经检验,或均为所列方程的根,
(1)当时,,
则的面积为;
(2)当时,,
则的面积为;
综上,的面积为或,
9.已知抛物线与轴有两个交点,,抛物线与轴的一个交点是,则的值是( )
A.5 B. C.5或1 D.或
【答案】C
解:比较抛物线与抛物线,
发现:将前一个抛物线往右平移m个单位后可以得到后一个抛物线的解析式,
∵,与轴的一个交点是,与轴有两个交点,,
∴当前一个抛物线往右平移1个单位时,后一个抛物线与轴的一个交点是,故m=1,
当前一个抛物线往右平移5个单位时,后一个抛物线与轴的一个交点是,故m=5,
10.如图,在中,,以点A为圆心,3为半径的圆与边相切于点D,与,分别交于点E和点G,点F是优弧上一点,,则的度数是( )
A.50° B.48° C.45° D.36°
【答案】B
解:连接AD,则AD=AG=3,
∵BC与圆A相切于点D,
∴∠ADB=∠ADC=90°,
在Rt△ADB中,AB=6,则cos∠BAD==,
∴∠BAD=60°,
∵∠CDE=18°,
∴∠ADE=90°﹣18°=72°,
∵AD=AE,
∴∠ADE=∠AED=72°,
∴∠DAE=180°﹣2×72°=36°,
∴∠GAC=36°+60°=96°,
∴∠GFE=∠GAC=48°,
故选:B.
二、填空题(每小题3分,共18分)
11. 已知,是一元二次方程的两个实数根,则代数式的值等于 .
答案:2021
根据一元二次方程根的定义得到,则,再利用根与系数的关系得到,然后利用整体代入的方法计算.
12. 某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为__________元时,才能使每天所获销售利润最大.
【答案】11
解:设销售单价定为元,每天所获利润为元,
则
,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
13. 如图,正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于 .
【答案】α=30°
解:如图所示,连接OA,OB,OG,
由旋转的性质可得,AB=BG,∠ABE=∠CBG=α
∵正方形ABCD的边长和⊙O的半径相等,
∴OA=OB=OG=BG=AB,
∴△OAB和△OBG都是等边三角形,
∴∠OBA=∠OBG=60°,
∵∠ABO+∠OBG=∠ABC+∠CBG=120°,∠ABC=90°(正方形的性质),
∴∠CBG=30°,
∴α=30°,
14. 如图,在矩形中,,以点B为圆心,长为半径画弧,交于点E,则图中阴影部分的面积为_______.
【答案】
解:连接BE,如图所示:
由题意得BE=AB=2cm,
∵四边形ABCD是矩形,
∴,
∵,
∴,
∴∠EBC=30°,∠ABE=60°,
∴,
∴;
故答案为.
15. 如图,在中,D为BC上一点,,则的值为________.
【答案】.
16. 如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是 .
【答案】4
如图所示,
(1)为上一动点,点关于线段的对称点为点,连接,则,过点作的平行线,过点作的平行线,两平行线相交于点,与相交于点M.
四边形是平行四边形
则
(2)找一点, 连接,则,过点作的平行线,连接则.
此时
(1)中周长取到最小值
四边形是平行四边形
四边形是正方形
,
又,,
又
是等腰三角形
,则圆的半径,
三、解答题(8++8+8+8+8+10+10+12,共72分)
17. 已知关于x的一元二次方程.
(1)求证:无论k取何值,方程都有两个不相等的实数根.
(2)如果方程的两个实数根为,,且k与都为整数,求k所有可能的值.
【答案】(1)见解析;(2)0或-2或1或-1
【分析】
(1)计算判别式的值,然后根据判别式的意义得到结论;
(2)先利用因式分解法得出方程的两个根,再结合k与都为整数,得出k的值;
【详解】
解:(1)
∵△=
=
∴无论k取何值, 方程都有两个不相等的实数根.
(2)∵
∴
∴=0
∴,或,
当,时,
∵k与都为整数,
∴k=0或-2
当,时,
∴,
∵k与都为整数,
∴k=1或-1
∴k所有可能的值为0或-2或1或-1
18. 如图,直线分别交轴,轴于、两点,交反比例函数的图象于、两点.若,且的面积为4
(1)求的值;
(2)当点的横坐标为时,求的面积.
【答案】(1)-6;(2)8
解:(1)过作垂直于轴,垂足为,
∴,
∴.
∵,,
∴,,
∴,.
∴,,即.
(2)由(1)知,∴.
∵,∴,∴,.
设直线的解析式为,
将点、代入,得.
解得.
∴直线的解析式为.
联立方程组,解得,,
∴.
∴.
19. 如图,在菱形中,点M,N分别是边,上的点,,.连接,,延长交线段延长线于点E.
(1)求证:;
(2)若,则的长是__________.
【答案】(1)见解析;(2).
【分析】
(1)根据菱形的性质可得,,根据,,可得,利用即可证明;
(2)根据菱形的性质可证明,根据相似的性质可求得的长度,进而可求.
【解析】
解:(1)证明:四边形为菱形,
,,
,,
,
在和中,
,
,
(2)四边形为菱形,
,
,
,
,
,
,
,
,
,
,
,
.
20. 为了倡导“节约用水,从我做起”,某市政府决定对该市直属机关200户家庭用水情况进行调查.市政府调查小组随机抽查了其中部分家庭一年的月平均用水量(单位:吨),调查中发现,每户家庭月平均用水量在3~7吨范围内,并将调查结果制成了如下尚不完整的统计表:
月平均用水量(吨) 3 4 5 6 7
频数(户数) 4 9 10 7
频率 0.08 0.40 0.14
请根据统计表中提供的信息解答下列问题:
(1)填空:______,______,______.
(2)这些家庭中月平均用水量数据的平均数是______,众数是______,中位数是______.
(3)根据样本数据,估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户?
(4)市政府决定从月平均用水量最省的甲、乙丙丁四户家庭中,选取两户进行“节水”经验分享.请用列表或画树状图的方法,求出恰好选到甲、丙两户的概率,并列出所有等可能的结果.
【答案】(1)20;0.18;0.20;(2)4.92,4,5;(3)132户;(4),所有等可能结果为(甲,乙)、(甲,丙)、(甲,丁)、(乙,甲)、(乙,丙)、(乙,丁)、(丙,甲)、(丙,乙)、(丙,丁)、(丁,甲)、(丁,乙)(丁,丙)
解:(1)根据题意,被调查样本数为:
∴,,
故答案为:20;0.18;0.20;
(2)平均数是 ,
∵用水量为4吨的共20户,数量最多,
∴众数是4,
∵用水量共50组数据,中间的两个数均为5,
∴中位数是5
故答案为:4.92,4,5;
(3)∵,
∴(户)
∴月平均用水量不超过5吨的约有132户;
(4)画出树状图:
由树状图可以看出,所有可能出现的结果共有12种,即:(甲,乙)、(甲,丙)、(甲,丁)、(乙,甲)、(乙,丙)、(乙,丁)、(丙,甲)、(丙,乙)、(丙,丁)、(丁,甲)、(丁,乙)(丁,丙),这些结果出现的可能性相等.
其中恰好选到甲、丙两户的有2种.
∴(恰好选到甲、丙两户).
21. 如图1,在中,,,D为内一点,将线段AD绕点A逆时针旋转90°得到AE,连接CE,BD的延长线与CE交于点F.
(1)求证:,;
(2)如图2.连接AF,DC,已知,判断AF与DC的位置关系,并说明理由.
【答案】(1)见解析;(2),理由见解析
解(1)由旋转的性质,可得∠DAE=90°,AD=AE,
∵∠BAD+∠DAC=∠BAC=90°,∠CAE+∠DAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵
∴,即
∴
∴
∴,即;
(2),理由如下:
∵
∴
由(1)知,
∴A,D,F,E在以DE为直径的圆上,如图,
∵AD=AE
∴弧AD=弧AE,
∴
∴
∴;
22. 如图,在菱形中,是对角线上一点(),,垂足为,以为半径的分别交于点,交的延长线于点,与交于点.
(1)求证:是的切线;
(2)若是的中点,,.
①求的长;
②求的长.
【答案】(1)见解析;(2)①;②
(1)证明:如图,过点作于点,
∵是菱形的对角线,
∴,
∵,,
∴∠OEB=∠OMB=90 ,
∵OB=OB,
∴△OEB≌△OMB(AAS)
∴,
∴是的切线.
(2)解:①如图,
∵是的中点,,
∴.
∵,,
∴,
∴,
∴在Rt△OGH中,
∴∠GHO=30°,∠GOH=60°,
∴∠HOE=120°,
∵,∴,
∴由弧长公式,得到的长:.
②方法一:如图,过点作于点,
∵,
∴,
∴,
∴,
∵DG//NE,DN//GE,∠GEN=90
∴四边形NEGD是矩形,
∴NE=DG=1,BN=3,OE=4,DN=6,
在菱形中,AD=AB,在中,设,
∴,
∴.
方法二:如图,过作于点,
∵,,OE=OH=4,
∴,,,
∴,
∴.
23. 某工厂生产并销售A,B两种型号车床共14台,生产并销售1台A型车床可以获利10万元;如果生产并销售不超过4台B型车床,则每台B型车床可以获利17万元,如果超出4台B型车床,则每超出1台,每台B型车床获利将均减少1万元.设生产并销售B型车床台.
(1)当时,完成以下两个问题:
①请补全下面的表格:
A型 B型
车床数量/台 ________
每台车床获利/万元 10 ________
②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元,问:生产并销售B型车床多少台?
(2)当0<≤14时,设生产并销售A,B两种型号车床获得的总利润为W万元,如何分配生产并销售A,B两种车床的数量,使获得的总利润W最大?并求出最大利润.
【答案】(1)①,;②10台;(2)分配产销A型车床9台、B型车床5台;或产销A型车床8台、B型车床6台,此时可获得总利润最大值170万元
解:(1)当时,每台就要比17万元少()万元
所以每台获利,也就是()万元
①补全表格如下面:
A型 B型
车床数量/台
每台车床获利/万元 10
②此时,由A型获得的利润是10()万元,
由B型可获得利润为万元,
根据题意:, ,
,∵0≤≤14, ∴,
即应产销B型车床10台;
(2)当0≤≤4时,
当0≤≤4 A型 B型
车床数量/台
每台车床获利/万元 10 17
利润
此时,W=+=,
该函数值随着的增大而增大,当取最大值4时,W最大1=168(万元);
当4<≤14时,
当4<≤14 A型 B型
车床数量/台
每台车床获利/万元 10
利润
则W=+==,
当或时(均满足条件4<≤14),W达最大值W最大2=170(万元),
∵W最大2> W最大1,
∴应分配产销A型车床9台、B型车床5台;或产销A型车床8台、B型车床6台,此时可获得总利润最大值170万元.
24. 图1,二次函数的图象交坐标轴于点,,点为轴上一动点.
(1)求二次函数的表达式;
(2)过点作轴分别交线段,抛物线于点,,连接.当时,求的面积;
(3)如图2,将线段绕点逆时针旋转90得到线段.
①当点在抛物线上时,求点的坐标;
②点在抛物线上,连接,当平分时,直接写出点P的坐标.
【答案】(1);(2);(3)①或;②或.
解:(1)二次函数的图象经过
解得
(2)由,令
解得
当时,
,则
;
(3)如图,当点在轴下方时,过点作于点,
由,令,
解得
,
,
将线段绕点逆时针旋转90得到线段,
,,
设,
点在抛物线上,
解得(舍)
当点在轴上方时,如图,
过点作于点,设
同理可得
点在抛物线上,
解得(舍去),
综上所述,或;
②当不平行于轴时,过点作交于点,过点作于点,如图,
平分,,
,
,
,
当不平行于轴时,重合,
,
当轴时,如图,
此时
则
综上所述,当平方时,点的坐标为或.
九年级数学(上)·第 1 页 共 3 页
