2021-2022学年华师大版数学八年级上册第14章勾股定理 单元检测(word版含答案)
文档属性
| 名称 | 2021-2022学年华师大版数学八年级上册第14章勾股定理 单元检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 602.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 13:51:27 | ||
图片预览




文档简介
第14章勾股定理 单元评价检测
(120分钟 100分)
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(2020·铜仁中考)已知等边三角形一边上的高为2,则它的边长为 ( )
A.2 B.3 C.4 D.4
2.用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为 ( )
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
3.已知一直角三角形的木板,三边的平方和为12 800 cm2,则斜边长为 ( )
A.80 cm B.30 cm C.90 cm D.120 cm
4.(2021·厦门质检)若实数m,n满足|m-3|+=0,且m,n恰好是Rt△ABC的两条边长,则第三条边长为 ( )
A.5 B. C.5或 D.以上都不对
5.(2021·泉州模拟)如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是 ( )
A.16 B.25 C.144 D.169
6.如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130 m,BC=120 m,若每天凿隧道5 m,则把隧道凿通需要 ( )
A.10天 B.9天 C.8天 D.11天
7.(2021·三明质检)工人师傅从一根长90 cm的钢条上截取一段后恰好与两根长分别为60 cm、100 cm的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为 ( )
A.80 cm B. cm
C.80 cm或 cm D.60 cm
8.△ABC的三边分别为a,b,c,满足c2=a2+b2,c2-2b2=0,则这个三角形有一个角的度数为 ( )
A.135° B.75° C.45° D.30°
9.(2021·宁德质检)如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( )
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
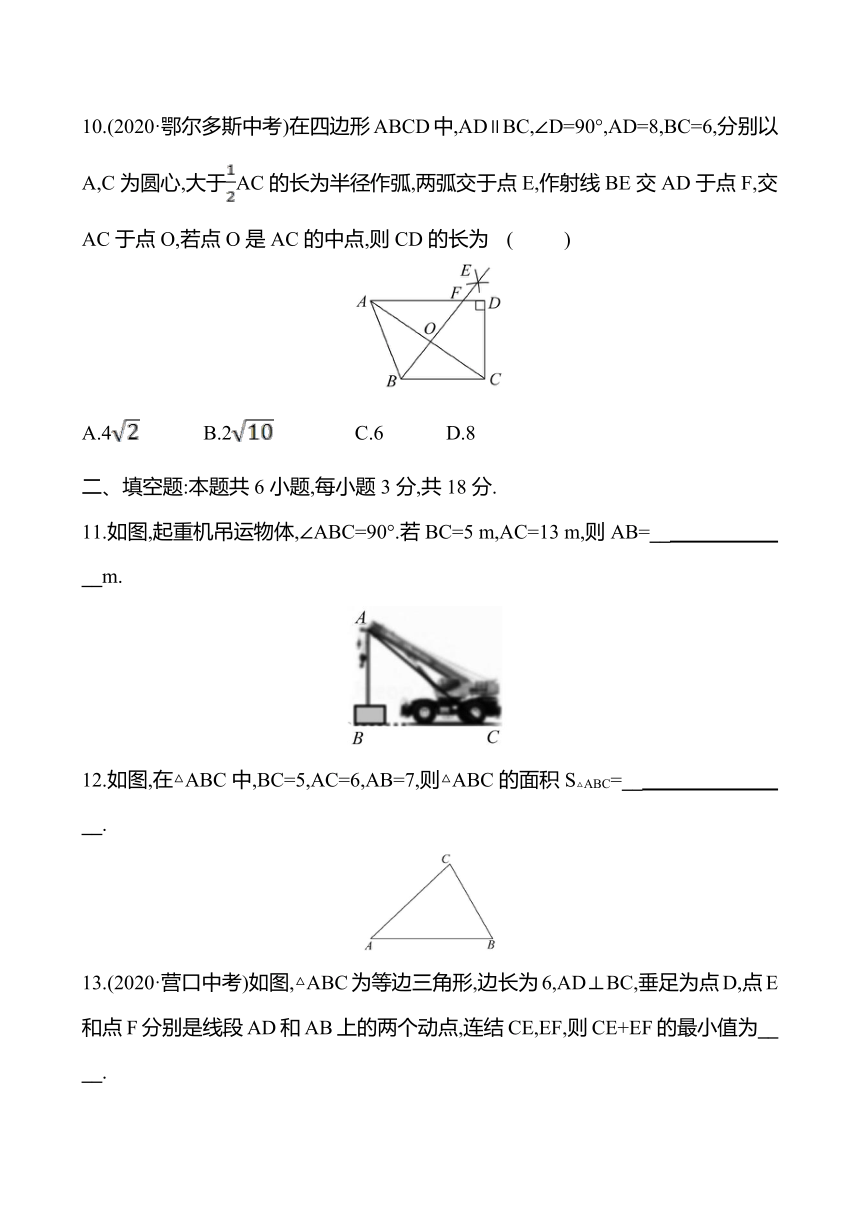
10.(2020·鄂尔多斯中考)在四边形ABCD中,AD∥BC,∠D=90°,AD=8,BC=6,分别以A,C为圆心,大于AC的长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O,若点O是AC的中点,则CD的长为 ( )
A.4 B.2 C.6 D.8
二、填空题:本题共6小题,每小题3分,共18分.
11.如图,起重机吊运物体,∠ABC=90°.若BC=5 m,AC=13 m,则AB=__ __m.
12.如图,在△ABC中,BC=5,AC=6,AB=7,则△ABC的面积S△ABC=__ __.
13.(2020·营口中考)如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连结CE,EF,则CE+EF的最小值为__ __.
14.已知△ABC的三边长为a,b,c,满足a+b=10,ab=18,c=8,则此三角形为__ __三角形.
15.2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为__ __.
16.如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是__ __.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分) 用反证法证明已知a<|a|,求证:a必为负数.
18.(6分)(2021·漳州质检)一写字楼发生火灾,消防车立即赶到距大楼12米的点A处,升起云梯到发生火灾的窗口点C处,已知云梯BC长20米,云梯底部B距地面A为3.2米,问发生火灾的窗口距地面有多少米
19.(6分)如图,一名将军带兵攻打一座城,城墙高23.6米,墙外有一条宽度为7米的护城河,将军军队里的攻城云梯长度均为25米,请你帮将军算一算,这些梯子的长度能否达到城墙的顶端
20.(8分)(2020·温州中考)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
21.(8分)(2021·泉州期末)如图,在5×4的正方形网格中,每个小正方形的边长都是1.
(1)分别求出AB,CD的长度;
(2)在图中作EF,使得EF的长为,以AB,CD,EF三条线段为边能否构成直角三角形,请说明理由.
22.(8分)如图,每个小正方形的边长为1.
(1)求图中格点三角形ABC的面积;
(2)判断△ABC的形状,并证明你的结论.
23.(10分)(2021·福州期末)如图,已知在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q分别为AB,BC边上的动点,点P从点A开始沿A→B方向运动,且速度为每秒1 cm,点Q从点B开始沿B→C方向运动,且速度为每秒2 cm,它们同时出发P到达B或Q到达C,即停止运动;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分 若能够,请求出运动时间;若不能够,请说明理由.
第14章勾股定理 单元评价检测
参考答案
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(2020·铜仁中考)已知等边三角形一边上的高为2,则它的边长为 (C)
A.2 B.3 C.4 D.4
2.用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为 (D)
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
3.已知一直角三角形的木板,三边的平方和为12 800 cm2,则斜边长为 (A)
A.80 cm B.30 cm C.90 cm D.120 cm
4.(2021·厦门质检)若实数m,n满足|m-3|+=0,且m,n恰好是Rt△ABC的两条边长,则第三条边长为 (C)
A.5 B. C.5或 D.以上都不对
5.(2021·泉州模拟)如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是 (B)
A.16 B.25 C.144 D.169
6.如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130 m,BC=120 m,若每天凿隧道5 m,则把隧道凿通需要 (A)
A.10天 B.9天 C.8天 D.11天
7.(2021·三明质检)工人师傅从一根长90 cm的钢条上截取一段后恰好与两根长分别为60 cm、100 cm的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为 (A)
A.80 cm B. cm
C.80 cm或 cm D.60 cm
8.△ABC的三边分别为a,b,c,满足c2=a2+b2,c2-2b2=0,则这个三角形有一个角的度数为 (C)
A.135° B.75° C.45° D.30°
9.(2021·宁德质检)如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 (C)
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
10.(2020·鄂尔多斯中考)在四边形ABCD中,AD∥BC,∠D=90°,AD=8,BC=6,分别以A,C为圆心,大于AC的长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O,若点O是AC的中点,则CD的长为 (A)
A.4 B.2 C.6 D.8
二、填空题:本题共6小题,每小题3分,共18分.
11.如图,起重机吊运物体,∠ABC=90°.若BC=5 m,AC=13 m,则AB=__12__m.
12.如图,在△ABC中,BC=5,AC=6,AB=7,则△ABC的面积S△ABC=__6__.
13.(2020·营口中考)如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连结CE,EF,则CE+EF的最小值为__3__.
14.已知△ABC的三边长为a,b,c,满足a+b=10,ab=18,c=8,则此三角形为__直角__三角形.
15.2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为__27__.
16.如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是__PB2+PA2=2PC2__.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分) 用反证法证明已知a<|a|,求证:a必为负数.
【证明】假设a不是负数,那么a是正数或a是零,
(1)如果a是零,那么a=|a|,这与题设矛盾,所以a不可能是零;
(2)如果a是正数,那么a=|a|,这与题设矛盾,所以a不可能是正数;
综合(1)和(2),知a不可能是正数,也不可能是零.所以a必为负数.
18.(6分)(2021·漳州质检)一写字楼发生火灾,消防车立即赶到距大楼12米的点A处,升起云梯到发生火灾的窗口点C处,已知云梯BC长20米,云梯底部B距地面A为3.2米,问发生火灾的窗口距地面有多少米
【解析】由题意可得:DC===16(m),又∵DH=BA=3.2米,则CH=DC+DH=16+3.2=19.2(m),
答:发生火灾的窗口距地面有19.2米.
19.(6分)如图,一名将军带兵攻打一座城,城墙高23.6米,墙外有一条宽度为7米的护城河,将军军队里的攻城云梯长度均为25米,请你帮将军算一算,这些梯子的长度能否达到城墙的顶端
【解析】能,理由如下:
设这把梯子能够到达的墙的最大高度是h米,则根据勾股定理得:h==24>23.6,
∴一架长为25米的云梯能够到达墙的顶端.
20.(8分)(2020·温州中考)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
【解析】(1)∵AB∥DE,∴∠BAC=∠D,
又∵∠B=∠DCE=90°,AC=DE,∴△ABC≌△DCE(AAS);
(2)∵△ABC≌△DCE,∴CE=BC=5,
∵∠ACE=90°,∴AE===13.
21.(8分)(2021·泉州期末)如图,在5×4的正方形网格中,每个小正方形的边长都是1.
(1)分别求出AB,CD的长度;
(2)在图中作EF,使得EF的长为,以AB,CD,EF三条线段为边能否构成直角三角形,请说明理由.
【解析】(1)AB= = ,CD==3;
(2)如图,EF==,
∵AB2+EF2=5+13=18,CD2=18,
∴AB2+EF2=CD2,
∴以AB,CD,EF三条线为边能构成直角三角形.
22.(8分)如图,每个小正方形的边长为1.
(1)求图中格点三角形ABC的面积;
(2)判断△ABC的形状,并证明你的结论.
【解析】(1)如图,S△ABC=S矩形ADEF-S△ABD-S△EBC-S△AFC
=6×5-×5×5-×3×1-×6×2
=30-12.5-1.5-6
=10;
(2)△ABC是直角三角形.理由如下:
∵AC2=62+22=40,BC2=32+12=10,AB2=52+52=50,
∴AC2+BC2=AB2,
∴∠ACB=90°,即△ABC是直角三角形.
23.(10分)(2021·福州期末)如图,已知在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q分别为AB,BC边上的动点,点P从点A开始沿A→B方向运动,且速度为每秒1 cm,点Q从点B开始沿B→C方向运动,且速度为每秒2 cm,它们同时出发P到达B或Q到达C,即停止运动;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分 若能够,请求出运动时间;若不能够,请说明理由.
【解析】(1)出发2秒后则AP=2,BQ=4,
∴BP=AB-AP=8-2=6,在Rt△BPQ中,∠B=90°,由勾股定理,得PQ==2 cm;
(2)设时间为t1,列方程得2t1=8-1×t1,解得t1=;
答:出发秒钟后,△PQB能形成等腰三角形;
(3)假设直线PQ能把原三角形周长分成相等的两部分,由AB=8 cm,BC=6 cm,
根据勾股定理可知AC=10 cm,即三角形的周长为8+6+10=24 cm,
则有BP+BQ=×24=12,
设时间为t2,列方程得:2t2+(8-1×t2)=12,解得t2=4,
当t2=4时,点Q运动的路程是4×2=8>6,
所以直线PQ不能够把原三角形周长分成相等的两部分.
(120分钟 100分)
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(2020·铜仁中考)已知等边三角形一边上的高为2,则它的边长为 ( )
A.2 B.3 C.4 D.4
2.用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为 ( )
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
3.已知一直角三角形的木板,三边的平方和为12 800 cm2,则斜边长为 ( )
A.80 cm B.30 cm C.90 cm D.120 cm
4.(2021·厦门质检)若实数m,n满足|m-3|+=0,且m,n恰好是Rt△ABC的两条边长,则第三条边长为 ( )
A.5 B. C.5或 D.以上都不对
5.(2021·泉州模拟)如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是 ( )
A.16 B.25 C.144 D.169
6.如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130 m,BC=120 m,若每天凿隧道5 m,则把隧道凿通需要 ( )
A.10天 B.9天 C.8天 D.11天
7.(2021·三明质检)工人师傅从一根长90 cm的钢条上截取一段后恰好与两根长分别为60 cm、100 cm的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为 ( )
A.80 cm B. cm
C.80 cm或 cm D.60 cm
8.△ABC的三边分别为a,b,c,满足c2=a2+b2,c2-2b2=0,则这个三角形有一个角的度数为 ( )
A.135° B.75° C.45° D.30°
9.(2021·宁德质检)如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 ( )
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
10.(2020·鄂尔多斯中考)在四边形ABCD中,AD∥BC,∠D=90°,AD=8,BC=6,分别以A,C为圆心,大于AC的长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O,若点O是AC的中点,则CD的长为 ( )
A.4 B.2 C.6 D.8
二、填空题:本题共6小题,每小题3分,共18分.
11.如图,起重机吊运物体,∠ABC=90°.若BC=5 m,AC=13 m,则AB=__ __m.
12.如图,在△ABC中,BC=5,AC=6,AB=7,则△ABC的面积S△ABC=__ __.
13.(2020·营口中考)如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连结CE,EF,则CE+EF的最小值为__ __.
14.已知△ABC的三边长为a,b,c,满足a+b=10,ab=18,c=8,则此三角形为__ __三角形.
15.2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为__ __.
16.如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是__ __.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分) 用反证法证明已知a<|a|,求证:a必为负数.
18.(6分)(2021·漳州质检)一写字楼发生火灾,消防车立即赶到距大楼12米的点A处,升起云梯到发生火灾的窗口点C处,已知云梯BC长20米,云梯底部B距地面A为3.2米,问发生火灾的窗口距地面有多少米
19.(6分)如图,一名将军带兵攻打一座城,城墙高23.6米,墙外有一条宽度为7米的护城河,将军军队里的攻城云梯长度均为25米,请你帮将军算一算,这些梯子的长度能否达到城墙的顶端
20.(8分)(2020·温州中考)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
21.(8分)(2021·泉州期末)如图,在5×4的正方形网格中,每个小正方形的边长都是1.
(1)分别求出AB,CD的长度;
(2)在图中作EF,使得EF的长为,以AB,CD,EF三条线段为边能否构成直角三角形,请说明理由.
22.(8分)如图,每个小正方形的边长为1.
(1)求图中格点三角形ABC的面积;
(2)判断△ABC的形状,并证明你的结论.
23.(10分)(2021·福州期末)如图,已知在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q分别为AB,BC边上的动点,点P从点A开始沿A→B方向运动,且速度为每秒1 cm,点Q从点B开始沿B→C方向运动,且速度为每秒2 cm,它们同时出发P到达B或Q到达C,即停止运动;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分 若能够,请求出运动时间;若不能够,请说明理由.
第14章勾股定理 单元评价检测
参考答案
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.(2020·铜仁中考)已知等边三角形一边上的高为2,则它的边长为 (C)
A.2 B.3 C.4 D.4
2.用反证法证明命题:“若a,b是整数,ab能被3整除,那么a,b中至少有一个能被3整除”时,假设应为 (D)
A.a,b都能被3整除 B.a不能被3整除
C.a,b不都能被3整除 D.a,b都不能被3整除
3.已知一直角三角形的木板,三边的平方和为12 800 cm2,则斜边长为 (A)
A.80 cm B.30 cm C.90 cm D.120 cm
4.(2021·厦门质检)若实数m,n满足|m-3|+=0,且m,n恰好是Rt△ABC的两条边长,则第三条边长为 (C)
A.5 B. C.5或 D.以上都不对
5.(2021·泉州模拟)如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是 (B)
A.16 B.25 C.144 D.169
6.如图,为修铁路需凿隧道AC,测得∠A+∠B=90°,AB=130 m,BC=120 m,若每天凿隧道5 m,则把隧道凿通需要 (A)
A.10天 B.9天 C.8天 D.11天
7.(2021·三明质检)工人师傅从一根长90 cm的钢条上截取一段后恰好与两根长分别为60 cm、100 cm的钢条一起焊接成一个直角三角形钢架,则截取下来的钢条长应为 (A)
A.80 cm B. cm
C.80 cm或 cm D.60 cm
8.△ABC的三边分别为a,b,c,满足c2=a2+b2,c2-2b2=0,则这个三角形有一个角的度数为 (C)
A.135° B.75° C.45° D.30°
9.(2021·宁德质检)如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是 (C)
A.5≤a≤12 B.5≤a≤13 C.12≤a≤13 D.12≤a≤15
10.(2020·鄂尔多斯中考)在四边形ABCD中,AD∥BC,∠D=90°,AD=8,BC=6,分别以A,C为圆心,大于AC的长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O,若点O是AC的中点,则CD的长为 (A)
A.4 B.2 C.6 D.8
二、填空题:本题共6小题,每小题3分,共18分.
11.如图,起重机吊运物体,∠ABC=90°.若BC=5 m,AC=13 m,则AB=__12__m.
12.如图,在△ABC中,BC=5,AC=6,AB=7,则△ABC的面积S△ABC=__6__.
13.(2020·营口中考)如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连结CE,EF,则CE+EF的最小值为__3__.
14.已知△ABC的三边长为a,b,c,满足a+b=10,ab=18,c=8,则此三角形为__直角__三角形.
15.2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是15,小正方形的面积是3,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,那么图2中最大的正方形的面积为__27__.
16.如图,在△ABC中,∠ACB=90°,AC=BC,点P在斜边AB上,以PC为直角边作等腰直角三角形PCQ,∠PCQ=90°,则PA2,PB2,PC2三者之间的数量关系是__PB2+PA2=2PC2__.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分) 用反证法证明已知a<|a|,求证:a必为负数.
【证明】假设a不是负数,那么a是正数或a是零,
(1)如果a是零,那么a=|a|,这与题设矛盾,所以a不可能是零;
(2)如果a是正数,那么a=|a|,这与题设矛盾,所以a不可能是正数;
综合(1)和(2),知a不可能是正数,也不可能是零.所以a必为负数.
18.(6分)(2021·漳州质检)一写字楼发生火灾,消防车立即赶到距大楼12米的点A处,升起云梯到发生火灾的窗口点C处,已知云梯BC长20米,云梯底部B距地面A为3.2米,问发生火灾的窗口距地面有多少米
【解析】由题意可得:DC===16(m),又∵DH=BA=3.2米,则CH=DC+DH=16+3.2=19.2(m),
答:发生火灾的窗口距地面有19.2米.
19.(6分)如图,一名将军带兵攻打一座城,城墙高23.6米,墙外有一条宽度为7米的护城河,将军军队里的攻城云梯长度均为25米,请你帮将军算一算,这些梯子的长度能否达到城墙的顶端
【解析】能,理由如下:
设这把梯子能够到达的墙的最大高度是h米,则根据勾股定理得:h==24>23.6,
∴一架长为25米的云梯能够到达墙的顶端.
20.(8分)(2020·温州中考)如图,在△ABC和△DCE中,AC=DE,∠B=∠DCE=90°,点A,C,D依次在同一直线上,且AB∥DE.
(1)求证:△ABC≌△DCE;
(2)连结AE,当BC=5,AC=12时,求AE的长.
【解析】(1)∵AB∥DE,∴∠BAC=∠D,
又∵∠B=∠DCE=90°,AC=DE,∴△ABC≌△DCE(AAS);
(2)∵△ABC≌△DCE,∴CE=BC=5,
∵∠ACE=90°,∴AE===13.
21.(8分)(2021·泉州期末)如图,在5×4的正方形网格中,每个小正方形的边长都是1.
(1)分别求出AB,CD的长度;
(2)在图中作EF,使得EF的长为,以AB,CD,EF三条线段为边能否构成直角三角形,请说明理由.
【解析】(1)AB= = ,CD==3;
(2)如图,EF==,
∵AB2+EF2=5+13=18,CD2=18,
∴AB2+EF2=CD2,
∴以AB,CD,EF三条线为边能构成直角三角形.
22.(8分)如图,每个小正方形的边长为1.
(1)求图中格点三角形ABC的面积;
(2)判断△ABC的形状,并证明你的结论.
【解析】(1)如图,S△ABC=S矩形ADEF-S△ABD-S△EBC-S△AFC
=6×5-×5×5-×3×1-×6×2
=30-12.5-1.5-6
=10;
(2)△ABC是直角三角形.理由如下:
∵AC2=62+22=40,BC2=32+12=10,AB2=52+52=50,
∴AC2+BC2=AB2,
∴∠ACB=90°,即△ABC是直角三角形.
23.(10分)(2021·福州期末)如图,已知在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,P,Q分别为AB,BC边上的动点,点P从点A开始沿A→B方向运动,且速度为每秒1 cm,点Q从点B开始沿B→C方向运动,且速度为每秒2 cm,它们同时出发P到达B或Q到达C,即停止运动;设出发的时间为t秒.
(1)出发2秒后,求PQ的长;
(2)从出发几秒钟后,△PQB能形成等腰三角形
(3)在运动过程中,直线PQ能否把原三角形周长分成相等的两部分 若能够,请求出运动时间;若不能够,请说明理由.
【解析】(1)出发2秒后则AP=2,BQ=4,
∴BP=AB-AP=8-2=6,在Rt△BPQ中,∠B=90°,由勾股定理,得PQ==2 cm;
(2)设时间为t1,列方程得2t1=8-1×t1,解得t1=;
答:出发秒钟后,△PQB能形成等腰三角形;
(3)假设直线PQ能把原三角形周长分成相等的两部分,由AB=8 cm,BC=6 cm,
根据勾股定理可知AC=10 cm,即三角形的周长为8+6+10=24 cm,
则有BP+BQ=×24=12,
设时间为t2,列方程得:2t2+(8-1×t2)=12,解得t2=4,
当t2=4时,点Q运动的路程是4×2=8>6,
所以直线PQ不能够把原三角形周长分成相等的两部分.
