2021-2022学年华师大版数学八年级上册第13章全等三角形 单元检测(word版含答案)
文档属性
| 名称 | 2021-2022学年华师大版数学八年级上册第13章全等三角形 单元检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 611.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 13:54:26 | ||
图片预览



文档简介
第13章全等三角形 单元评价检测
(90分钟 100分)
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.为说明命题“若a>b,则a2>b2.”是假命题,所列举反例正确的是 ( )
A.a=5,b=3 B.a=-2,b=-6
C.a=0.2,b=0.1 D.a=-,b=-
2.(2020·河池中考)观察下列作图痕迹,所作CD为△ABC的边AB上的中线是 ( )
3.下列命题是真命题的是 ( )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短
B.互补的角是邻补角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
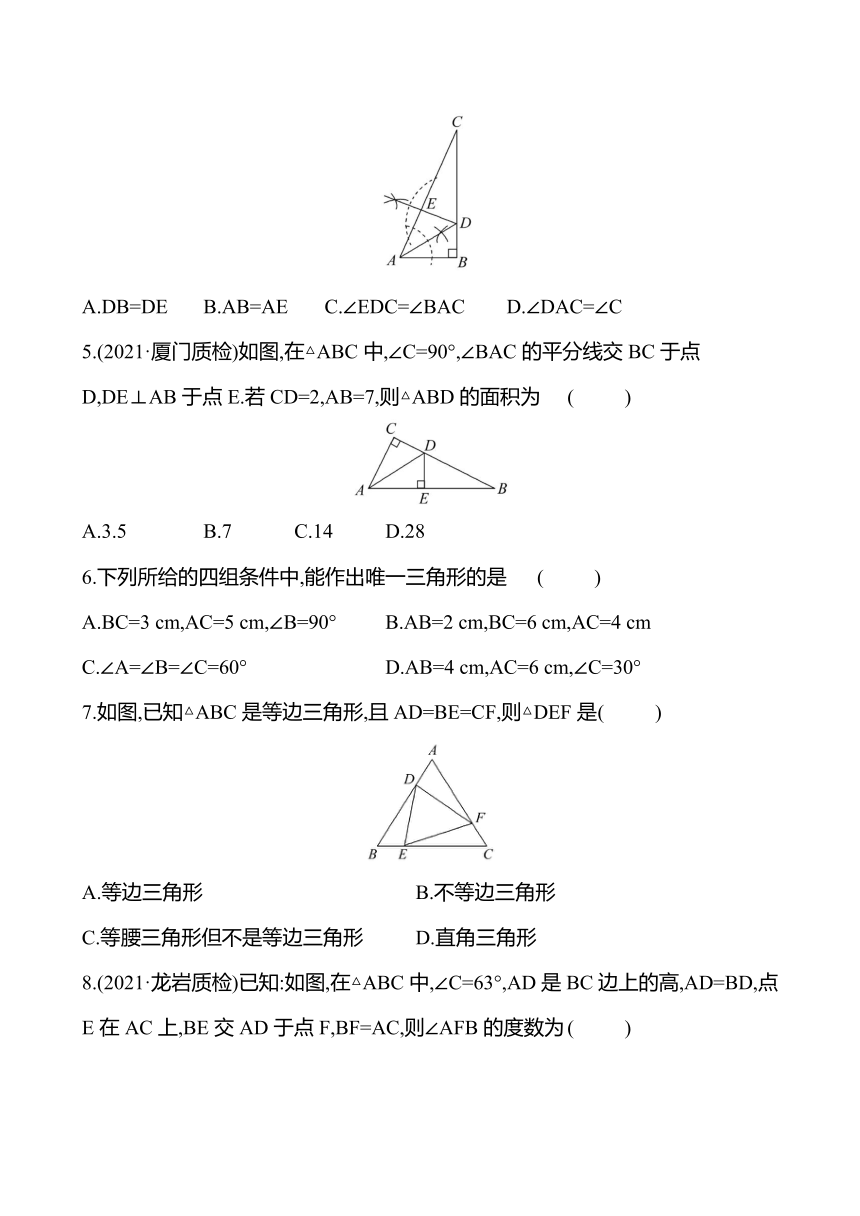
4.(2020·襄阳中考)如图,在Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是 ( )
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
5.(2021·厦门质检)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AB于点E.若CD=2,AB=7,则△ABD的面积为 ( )
A.3.5 B.7 C.14 D.28
6.下列所给的四组条件中,能作出唯一三角形的是 ( )
A.BC=3 cm,AC=5 cm,∠B=90° B.AB=2 cm,BC=6 cm,AC=4 cm
C.∠A=∠B=∠C=60° D.AB=4 cm,AC=6 cm,∠C=30°
7.如图,已知△ABC是等边三角形,且AD=BE=CF,则△DEF是 ( )
A.等边三角形 B.不等边三角形
C.等腰三角形但不是等边三角形 D.直角三角形
8.(2021·龙岩质检)已知:如图,在△ABC中,∠C=63°,AD是BC边上的高,AD=BD,点E在AC上,BE交AD于点F,BF=AC,则∠AFB的度数为 ( )
A.27° B.37° C.63° D.117°
9.如图,在△ABC与△EMN中,BC=MN=a,AC=EM=b,AB=c,∠C=∠M=54°.若∠A=66°,下列结论正确的是 ( )
A.EN=c B.EN=a C.∠E=60° D.∠N=66°
10.(2021·南平期末)如图,已知:∠MON=30°,点A1,A2,A3……在射线ON上,点B1,B2,B3……在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4……均为等边三角形,若OA1=,则△A6B6A7的边长为 ( )
A.6 B.12 C.16 D.32
二、填空题:本题共6小题,每小题3分,共18分.
11.写出命题“直角三角形的两个锐角互余”的逆命题:__ __.
12.若实数x,y满足|x-4|+=0,则以x,y的值为边长的等腰三角形的周长为__ __.
13.(2021·泉州质检)如图,若△ABC≌△DEF,且∠B=60°,∠F-∠D=56°,则∠A=__ __.
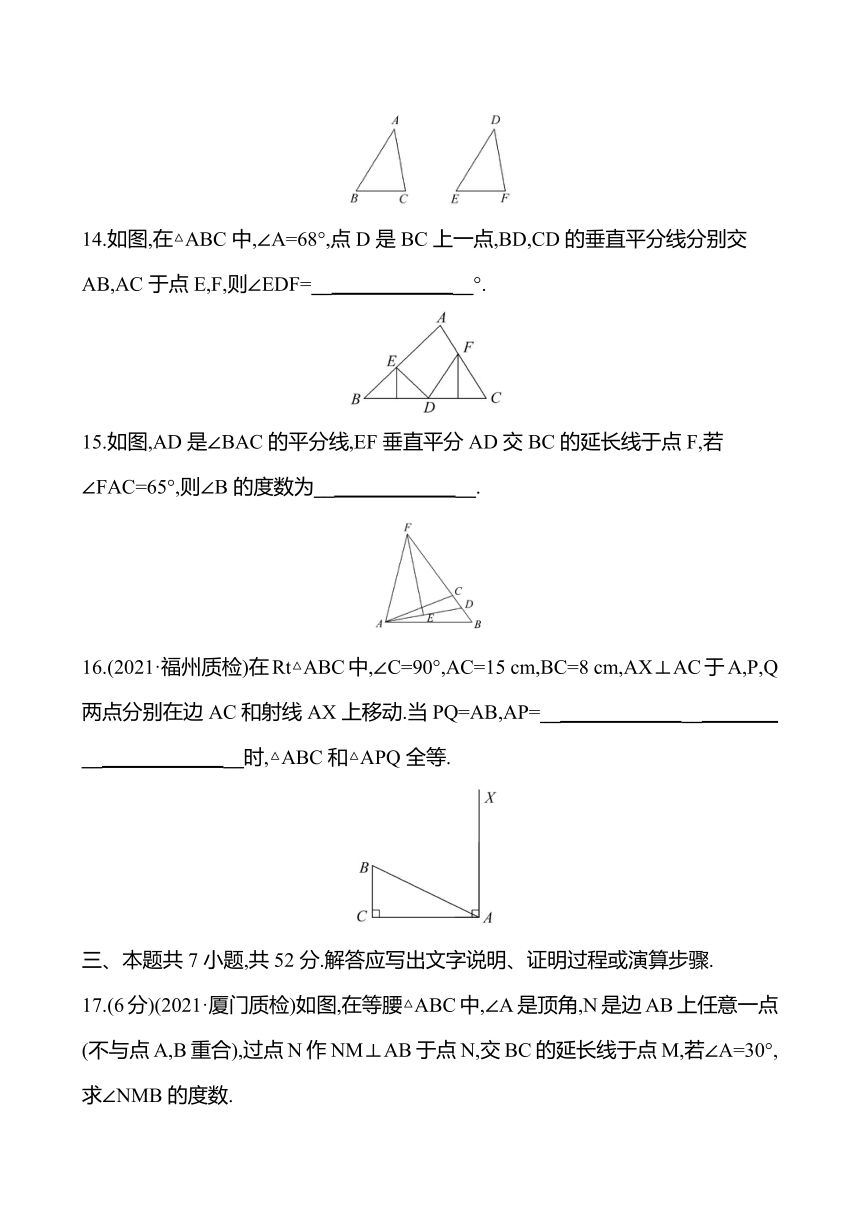
14.如图,在△ABC中,∠A=68°,点D是BC上一点,BD,CD的垂直平分线分别交AB,AC于点E,F,则∠EDF=__ __°.
15.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为__ __.
16.(2021·福州质检)在Rt△ABC中,∠C=90°,AC=15 cm,BC=8 cm,AX⊥AC于A,P,Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=__ __ __ __时,△ABC和△APQ全等.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)(2021·厦门质检)如图,在等腰△ABC中,∠A是顶角,N是边AB上任意一点(不与点A,B重合),过点N作NM⊥AB于点N,交BC的延长线于点M,若∠A=30°,求∠NMB的度数.
18.(6分)(2020·广州中考)如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°.求∠BCA的度数.
19.(8分)(1)完成下面的推理说明:
已知:如图,BE∥CF,BE,CF分别平分∠ABC和∠BCD.求证:AB∥CD.
证明:∵BE,CF分别平分∠ABC和∠BCD(已知),
∴∠1=∠________,∠2=∠________(______________),
∵BE∥CF(________),
∴∠1=∠2(____________________),
∴∠ABC=∠BCD(________),
∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(____________________);
(2)说出(1)的推理中运用了哪两个互逆的真命题.
20.(8分)(2021·宁德质检)如图所示,已知锐角∠AOB及一点P.
(1)过点P作OA,OB的垂线,垂足分别是M,N;(只作图,保留作图痕迹,不写作法)
(2)猜想∠MPN与∠AOB之间的关系,并证明.
21.(8分)如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
(1)求证:AF=DE;
(2)若OM平分∠EOF,求证:OM⊥EF.
22.(8分)(2021·南平模拟) 如图,已知在△ABC中,AB=AC,点D,E分别在AC,AB上,且AD=AE,点F在BC的延长线上,DB=DF.
(1)求证:∠ABD=∠ACE;
(2)求证:CE∥DF.
23.(8分)(2020·凉山州中考)如图,点P、点Q分别是等边△ABC边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连结AQ,CP.求证:△ABQ≌△CAP;
(2)如图1,当点P,点Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点P,点Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数.
第13章全等三角形 单元评价检测
参考答案
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.为说明命题“若a>b,则a2>b2.”是假命题,所列举反例正确的是 (B)
A.a=5,b=3 B.a=-2,b=-6
C.a=0.2,b=0.1 D.a=-,b=-
2.(2020·河池中考)观察下列作图痕迹,所作CD为△ABC的边AB上的中线是 (B)
3.下列命题是真命题的是 (A)
A.连结直线外一点与直线上各点的所有线段中,垂线段最短
B.互补的角是邻补角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
4.(2020·襄阳中考)如图,在Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是 (D)
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
5.(2021·厦门质检)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AB于点E.若CD=2,AB=7,则△ABD的面积为 (B)
A.3.5 B.7 C.14 D.28
6.下列所给的四组条件中,能作出唯一三角形的是 (A)
A.BC=3 cm,AC=5 cm,∠B=90° B.AB=2 cm,BC=6 cm,AC=4 cm
C.∠A=∠B=∠C=60° D.AB=4 cm,AC=6 cm,∠C=30°
7.如图,已知△ABC是等边三角形,且AD=BE=CF,则△DEF是 (A)
A.等边三角形 B.不等边三角形
C.等腰三角形但不是等边三角形 D.直角三角形
8.(2021·龙岩质检)已知:如图,在△ABC中,∠C=63°,AD是BC边上的高,AD=BD,点E在AC上,BE交AD于点F,BF=AC,则∠AFB的度数为 (D)
A.27° B.37° C.63° D.117°
9.如图,在△ABC与△EMN中,BC=MN=a,AC=EM=b,AB=c,∠C=∠M=54°.若∠A=66°,下列结论正确的是 (A)
A.EN=c B.EN=a C.∠E=60° D.∠N=66°
10.(2021·南平期末)如图,已知:∠MON=30°,点A1,A2,A3……在射线ON上,点B1,B2,B3……在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4……均为等边三角形,若OA1=,则△A6B6A7的边长为 (C)
A.6 B.12 C.16 D.32
二、填空题:本题共6小题,每小题3分,共18分.
11.写出命题“直角三角形的两个锐角互余”的逆命题:__两个锐角互余的三角形是直角三角形__.
12.若实数x,y满足|x-4|+=0,则以x,y的值为边长的等腰三角形的周长为__22__.
13.(2021·泉州质检)如图,若△ABC≌△DEF,且∠B=60°,∠F-∠D=56°,则∠A=__32__.
14.如图,在△ABC中,∠A=68°,点D是BC上一点,BD,CD的垂直平分线分别交AB,AC于点E,F,则∠EDF=__68__°.
15.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为__65°__.
16.(2021·福州质检)在Rt△ABC中,∠C=90°,AC=15 cm,BC=8 cm,AX⊥AC于A,P,Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=__8__cm或15__cm__时,△ABC和△APQ全等.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)(2021·厦门质检)如图,在等腰△ABC中,∠A是顶角,N是边AB上任意一点(不与点A,B重合),过点N作NM⊥AB于点N,交BC的延长线于点M,若∠A=30°,求∠NMB的度数.
【解析】∵AB=AC,∴∠B=∠ACB,∴∠B==90°-∠A,
∵MN⊥AB,∴∠BNM=90°,∴∠NMB=90°-∠B=∠A=15°.
18.(6分)(2020·广州中考)如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°.求∠BCA的度数.
【解析】在△ABC与△ADC中,,
∴△ABC≌△ADC(S.A.S.),∴∠D=∠B=80°,∴∠BCA=180°-25°-80°=75°.
19.(8分)(1)完成下面的推理说明:
已知:如图,BE∥CF,BE,CF分别平分∠ABC和∠BCD.求证:AB∥CD.
证明:∵BE,CF分别平分∠ABC和∠BCD(已知),
∴∠1=∠________,∠2=∠________(______________),
∵BE∥CF(________),
∴∠1=∠2(____________________),
∴∠ABC=∠BCD(________),
∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(____________________);
(2)说出(1)的推理中运用了哪两个互逆的真命题.
【解析】(1)∵BE,CF分别平分∠ABC和∠BCD(已知),∴∠1=∠ABC,∠2=∠BCD(角平分线的定义),∵BE∥CF(已知),∴∠1=∠2(两直线平行,内错角相等),
∴∠ABC=∠BCD(等量代换),∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(内错角相等,两直线平行);
答案:(1)ABC BCD 角平分线的定义 已知 两直线平行,内错角相等 等量代换 内错角相等,两直线平行;
(2)两个互逆的真命题为:两直线平行,内错角相等;内错角相等,两直线平行.
20.(8分)(2021·宁德质检)如图所示,已知锐角∠AOB及一点P.
(1)过点P作OA,OB的垂线,垂足分别是M,N;(只作图,保留作图痕迹,不写作法)
(2)猜想∠MPN与∠AOB之间的关系,并证明.
【解析】(1)过点P作OA,OB的垂线PM,PN如图所示:
(2)猜想:∠MPN+∠AOB=180°或∠MPN=∠AOB.
理由:在(1)的左图中,在四边形PMON中,∵∠PMO=∠PNO=90°,
∴∠MPN+∠AOB=180°;在(1)的右图中,∵∠PJM=∠OJN,∠AMJ=∠JNO=90°,∴∠MPN=∠AOB.
21.(8分)如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
(1)求证:AF=DE;
(2)若OM平分∠EOF,求证:OM⊥EF.
【证明】(1)∵BE=CF,∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,,
∴Rt△ABF≌Rt△DCE(H.L.),∴AF=DE;
(2)由(1)得:Rt△ABF≌Rt△DCE,∴∠AFB=∠DEC,∴OE=OF,
∵OM平分∠EOF,∴OM⊥EF.
22.(8分)(2021·南平模拟) 如图,已知在△ABC中,AB=AC,点D,E分别在AC,AB上,且AD=AE,点F在BC的延长线上,DB=DF.
(1)求证:∠ABD=∠ACE;
(2)求证:CE∥DF.
【证明】(1)根据题意得
在△ADB和△AEC中,,
∴△ADB≌△AEC(S.A.S.),∴∠ABD=∠ACE;
(2)∵DB=DF,∴∠DBF=∠F,
∵∠ABC=∠ABD+∠DBC,∠ACB=∠F+∠CDF,
∴∠ABD=∠CDF,∴∠ACE=∠CDF,∴CE∥DF.
23.(8分)(2020·凉山州中考)如图,点P、点Q分别是等边△ABC边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连结AQ,CP.求证:△ABQ≌△CAP;
(2)如图1,当点P,点Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点P,点Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数.
【解析】(1)证明:如图1,∵△ABC是等边三角形,∴∠ABQ=∠CAP=60°,AB=CA,
又∵点P、点Q运动速度相同,∴AP=BQ,
在△ABQ与△CAP中,,
∴△ABQ≌△CAP(S.A.S.);
(2)点P,点Q在AB,BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC是△ACM的外角,∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC,
∵∠BAC=60°,∴∠QMC=60°;
(3)如图2,点P,点Q运动时,∠QMC不变.
理由:同理可得,△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°,
即点P,点Q,AB,BC的延长线上运动时,∠QMC的度数为120°.
(90分钟 100分)
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.为说明命题“若a>b,则a2>b2.”是假命题,所列举反例正确的是 ( )
A.a=5,b=3 B.a=-2,b=-6
C.a=0.2,b=0.1 D.a=-,b=-
2.(2020·河池中考)观察下列作图痕迹,所作CD为△ABC的边AB上的中线是 ( )
3.下列命题是真命题的是 ( )
A.连结直线外一点与直线上各点的所有线段中,垂线段最短
B.互补的角是邻补角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
4.(2020·襄阳中考)如图,在Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是 ( )
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
5.(2021·厦门质检)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AB于点E.若CD=2,AB=7,则△ABD的面积为 ( )
A.3.5 B.7 C.14 D.28
6.下列所给的四组条件中,能作出唯一三角形的是 ( )
A.BC=3 cm,AC=5 cm,∠B=90° B.AB=2 cm,BC=6 cm,AC=4 cm
C.∠A=∠B=∠C=60° D.AB=4 cm,AC=6 cm,∠C=30°
7.如图,已知△ABC是等边三角形,且AD=BE=CF,则△DEF是 ( )
A.等边三角形 B.不等边三角形
C.等腰三角形但不是等边三角形 D.直角三角形
8.(2021·龙岩质检)已知:如图,在△ABC中,∠C=63°,AD是BC边上的高,AD=BD,点E在AC上,BE交AD于点F,BF=AC,则∠AFB的度数为 ( )
A.27° B.37° C.63° D.117°
9.如图,在△ABC与△EMN中,BC=MN=a,AC=EM=b,AB=c,∠C=∠M=54°.若∠A=66°,下列结论正确的是 ( )
A.EN=c B.EN=a C.∠E=60° D.∠N=66°
10.(2021·南平期末)如图,已知:∠MON=30°,点A1,A2,A3……在射线ON上,点B1,B2,B3……在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4……均为等边三角形,若OA1=,则△A6B6A7的边长为 ( )
A.6 B.12 C.16 D.32
二、填空题:本题共6小题,每小题3分,共18分.
11.写出命题“直角三角形的两个锐角互余”的逆命题:__ __.
12.若实数x,y满足|x-4|+=0,则以x,y的值为边长的等腰三角形的周长为__ __.
13.(2021·泉州质检)如图,若△ABC≌△DEF,且∠B=60°,∠F-∠D=56°,则∠A=__ __.
14.如图,在△ABC中,∠A=68°,点D是BC上一点,BD,CD的垂直平分线分别交AB,AC于点E,F,则∠EDF=__ __°.
15.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为__ __.
16.(2021·福州质检)在Rt△ABC中,∠C=90°,AC=15 cm,BC=8 cm,AX⊥AC于A,P,Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=__ __ __ __时,△ABC和△APQ全等.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)(2021·厦门质检)如图,在等腰△ABC中,∠A是顶角,N是边AB上任意一点(不与点A,B重合),过点N作NM⊥AB于点N,交BC的延长线于点M,若∠A=30°,求∠NMB的度数.
18.(6分)(2020·广州中考)如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°.求∠BCA的度数.
19.(8分)(1)完成下面的推理说明:
已知:如图,BE∥CF,BE,CF分别平分∠ABC和∠BCD.求证:AB∥CD.
证明:∵BE,CF分别平分∠ABC和∠BCD(已知),
∴∠1=∠________,∠2=∠________(______________),
∵BE∥CF(________),
∴∠1=∠2(____________________),
∴∠ABC=∠BCD(________),
∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(____________________);
(2)说出(1)的推理中运用了哪两个互逆的真命题.
20.(8分)(2021·宁德质检)如图所示,已知锐角∠AOB及一点P.
(1)过点P作OA,OB的垂线,垂足分别是M,N;(只作图,保留作图痕迹,不写作法)
(2)猜想∠MPN与∠AOB之间的关系,并证明.
21.(8分)如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
(1)求证:AF=DE;
(2)若OM平分∠EOF,求证:OM⊥EF.
22.(8分)(2021·南平模拟) 如图,已知在△ABC中,AB=AC,点D,E分别在AC,AB上,且AD=AE,点F在BC的延长线上,DB=DF.
(1)求证:∠ABD=∠ACE;
(2)求证:CE∥DF.
23.(8分)(2020·凉山州中考)如图,点P、点Q分别是等边△ABC边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连结AQ,CP.求证:△ABQ≌△CAP;
(2)如图1,当点P,点Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点P,点Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数.
第13章全等三角形 单元评价检测
参考答案
一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合要求的.
1.为说明命题“若a>b,则a2>b2.”是假命题,所列举反例正确的是 (B)
A.a=5,b=3 B.a=-2,b=-6
C.a=0.2,b=0.1 D.a=-,b=-
2.(2020·河池中考)观察下列作图痕迹,所作CD为△ABC的边AB上的中线是 (B)
3.下列命题是真命题的是 (A)
A.连结直线外一点与直线上各点的所有线段中,垂线段最短
B.互补的角是邻补角
C.两条直线被第三条直线所截,同旁内角互补
D.过一点有且只有一条直线与已知直线平行
4.(2020·襄阳中考)如图,在Rt△ABC中,∠ABC=90°,根据尺规作图的痕迹判断以下结论错误的是 (D)
A.DB=DE B.AB=AE C.∠EDC=∠BAC D.∠DAC=∠C
5.(2021·厦门质检)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AB于点E.若CD=2,AB=7,则△ABD的面积为 (B)
A.3.5 B.7 C.14 D.28
6.下列所给的四组条件中,能作出唯一三角形的是 (A)
A.BC=3 cm,AC=5 cm,∠B=90° B.AB=2 cm,BC=6 cm,AC=4 cm
C.∠A=∠B=∠C=60° D.AB=4 cm,AC=6 cm,∠C=30°
7.如图,已知△ABC是等边三角形,且AD=BE=CF,则△DEF是 (A)
A.等边三角形 B.不等边三角形
C.等腰三角形但不是等边三角形 D.直角三角形
8.(2021·龙岩质检)已知:如图,在△ABC中,∠C=63°,AD是BC边上的高,AD=BD,点E在AC上,BE交AD于点F,BF=AC,则∠AFB的度数为 (D)
A.27° B.37° C.63° D.117°
9.如图,在△ABC与△EMN中,BC=MN=a,AC=EM=b,AB=c,∠C=∠M=54°.若∠A=66°,下列结论正确的是 (A)
A.EN=c B.EN=a C.∠E=60° D.∠N=66°
10.(2021·南平期末)如图,已知:∠MON=30°,点A1,A2,A3……在射线ON上,点B1,B2,B3……在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4……均为等边三角形,若OA1=,则△A6B6A7的边长为 (C)
A.6 B.12 C.16 D.32
二、填空题:本题共6小题,每小题3分,共18分.
11.写出命题“直角三角形的两个锐角互余”的逆命题:__两个锐角互余的三角形是直角三角形__.
12.若实数x,y满足|x-4|+=0,则以x,y的值为边长的等腰三角形的周长为__22__.
13.(2021·泉州质检)如图,若△ABC≌△DEF,且∠B=60°,∠F-∠D=56°,则∠A=__32__.
14.如图,在△ABC中,∠A=68°,点D是BC上一点,BD,CD的垂直平分线分别交AB,AC于点E,F,则∠EDF=__68__°.
15.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为__65°__.
16.(2021·福州质检)在Rt△ABC中,∠C=90°,AC=15 cm,BC=8 cm,AX⊥AC于A,P,Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=__8__cm或15__cm__时,△ABC和△APQ全等.
三、本题共7小题,共52分.解答应写出文字说明、证明过程或演算步骤.
17.(6分)(2021·厦门质检)如图,在等腰△ABC中,∠A是顶角,N是边AB上任意一点(不与点A,B重合),过点N作NM⊥AB于点N,交BC的延长线于点M,若∠A=30°,求∠NMB的度数.
【解析】∵AB=AC,∴∠B=∠ACB,∴∠B==90°-∠A,
∵MN⊥AB,∴∠BNM=90°,∴∠NMB=90°-∠B=∠A=15°.
18.(6分)(2020·广州中考)如图,AB=AD,∠BAC=∠DAC=25°,∠D=80°.求∠BCA的度数.
【解析】在△ABC与△ADC中,,
∴△ABC≌△ADC(S.A.S.),∴∠D=∠B=80°,∴∠BCA=180°-25°-80°=75°.
19.(8分)(1)完成下面的推理说明:
已知:如图,BE∥CF,BE,CF分别平分∠ABC和∠BCD.求证:AB∥CD.
证明:∵BE,CF分别平分∠ABC和∠BCD(已知),
∴∠1=∠________,∠2=∠________(______________),
∵BE∥CF(________),
∴∠1=∠2(____________________),
∴∠ABC=∠BCD(________),
∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(____________________);
(2)说出(1)的推理中运用了哪两个互逆的真命题.
【解析】(1)∵BE,CF分别平分∠ABC和∠BCD(已知),∴∠1=∠ABC,∠2=∠BCD(角平分线的定义),∵BE∥CF(已知),∴∠1=∠2(两直线平行,内错角相等),
∴∠ABC=∠BCD(等量代换),∴∠ABC=∠BCD(等式的性质),
∴AB∥CD(内错角相等,两直线平行);
答案:(1)ABC BCD 角平分线的定义 已知 两直线平行,内错角相等 等量代换 内错角相等,两直线平行;
(2)两个互逆的真命题为:两直线平行,内错角相等;内错角相等,两直线平行.
20.(8分)(2021·宁德质检)如图所示,已知锐角∠AOB及一点P.
(1)过点P作OA,OB的垂线,垂足分别是M,N;(只作图,保留作图痕迹,不写作法)
(2)猜想∠MPN与∠AOB之间的关系,并证明.
【解析】(1)过点P作OA,OB的垂线PM,PN如图所示:
(2)猜想:∠MPN+∠AOB=180°或∠MPN=∠AOB.
理由:在(1)的左图中,在四边形PMON中,∵∠PMO=∠PNO=90°,
∴∠MPN+∠AOB=180°;在(1)的右图中,∵∠PJM=∠OJN,∠AMJ=∠JNO=90°,∴∠MPN=∠AOB.
21.(8分)如图,∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
(1)求证:AF=DE;
(2)若OM平分∠EOF,求证:OM⊥EF.
【证明】(1)∵BE=CF,∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,,
∴Rt△ABF≌Rt△DCE(H.L.),∴AF=DE;
(2)由(1)得:Rt△ABF≌Rt△DCE,∴∠AFB=∠DEC,∴OE=OF,
∵OM平分∠EOF,∴OM⊥EF.
22.(8分)(2021·南平模拟) 如图,已知在△ABC中,AB=AC,点D,E分别在AC,AB上,且AD=AE,点F在BC的延长线上,DB=DF.
(1)求证:∠ABD=∠ACE;
(2)求证:CE∥DF.
【证明】(1)根据题意得
在△ADB和△AEC中,,
∴△ADB≌△AEC(S.A.S.),∴∠ABD=∠ACE;
(2)∵DB=DF,∴∠DBF=∠F,
∵∠ABC=∠ABD+∠DBC,∠ACB=∠F+∠CDF,
∴∠ABD=∠CDF,∴∠ACE=∠CDF,∴CE∥DF.
23.(8分)(2020·凉山州中考)如图,点P、点Q分别是等边△ABC边AB、BC上的动点(端点除外),点P、点Q以相同的速度,同时从点A、点B出发.
(1)如图1,连结AQ,CP.求证:△ABQ≌△CAP;
(2)如图1,当点P,点Q分别在AB,BC边上运动时,AQ,CP相交于点M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数;
(3)如图2,当点P,点Q在AB,BC的延长线上运动时,直线AQ,CP相交于M,∠QMC的大小是否变化 若变化,请说明理由;若不变,求出它的度数.
【解析】(1)证明:如图1,∵△ABC是等边三角形,∴∠ABQ=∠CAP=60°,AB=CA,
又∵点P、点Q运动速度相同,∴AP=BQ,
在△ABQ与△CAP中,,
∴△ABQ≌△CAP(S.A.S.);
(2)点P,点Q在AB,BC边上运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,
∵∠QMC是△ACM的外角,∴∠QMC=∠ACP+∠MAC=∠BAQ+∠MAC=∠BAC,
∵∠BAC=60°,∴∠QMC=60°;
(3)如图2,点P,点Q运动时,∠QMC不变.
理由:同理可得,△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC是△APM的外角,∴∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°,
即点P,点Q,AB,BC的延长线上运动时,∠QMC的度数为120°.
