2021-2022学年人教版七年级数学下册 5-3平行线的性质 寒假预习同步测评(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册 5-3平行线的性质 寒假预习同步测评(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 268.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 16:23:03 | ||
图片预览


文档简介
2021-2022学年人教版七年级数学下册《5-3平行线的性质》寒假预习同步测评(附答案)
一.选择题(共8小题,满分40分)
1.直角三角板与两边平行的纸条如图所示放置,下列结论不一定正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠2+∠4=90° D.∠1=∠4
2.如图,AB∥CD,∠MBN=3∠ABM,∠MDN=3∠CDM,∠N=160°,则∠M为( )
A.45° B.50° C.60° D.65°
3.如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )
A.5 B.6 C.7 D.8
4.如图,在四边形ABCD中,AB=AC=BD,AC与BD相交于H,且AC⊥BD.
①AB∥CD;②△ABD≌△BAC;③AB2+CD2=AD2+CB2;④∠ACB+∠BDA=135°.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
5.如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )
A.60° B.65° C.72° D.75°
6.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
7.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是( )
A.x+y+z=180° B.x﹣z=y C.y﹣x=z D.y﹣x=x﹣z
8.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
二.填空题(共8小题,满分40分)
9.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠BAC=90°),其中A,B两点分别落在直线m,n上,若∠2=52°,则∠1的度数为 .
10.如图所示,AB∥CD,∠1=56°,∠2=56°,则直线EF与GH的位置关系为 .
11.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 .
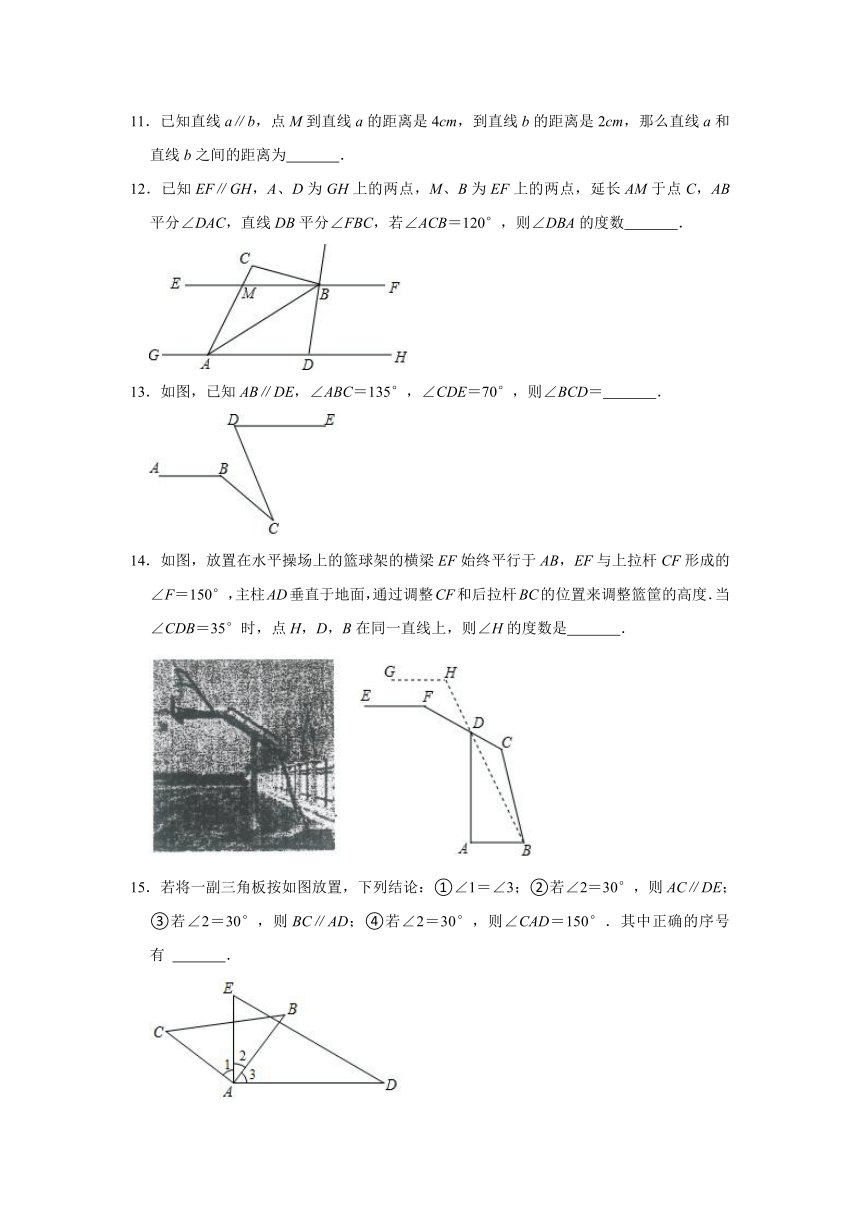
12.已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=120°,则∠DBA的度数 .
13.如图,已知AB∥DE,∠ABC=135°,∠CDE=70°,则∠BCD= .
14.如图,放置在水平操场上的篮球架的横梁EF始终平行于AB,EF与上拉杆CF形成的∠F=150°,主柱AD垂直于地面,通过调整CF和后拉杆BC的位置来调整篮筐的高度.当∠CDB=35°时,点H,D,B在同一直线上,则∠H的度数是 .
15.若将一副三角板按如图放置,下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④若∠2=30°,则∠CAD=150°.其中正确的序号有 .
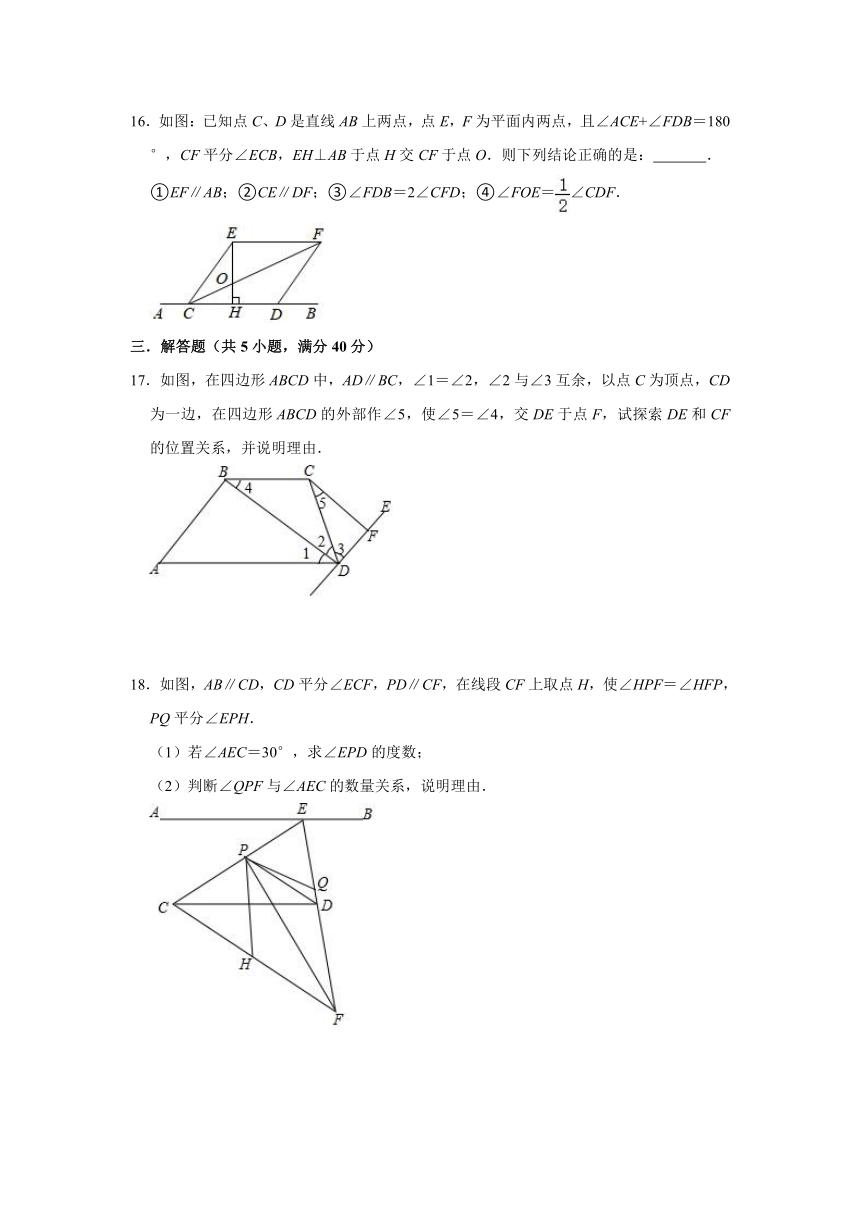
16.如图:已知点C、D是直线AB上两点,点E,F为平面内两点,且∠ACE+∠FDB=180°,CF平分∠ECB,EH⊥AB于点H交CF于点O.则下列结论正确的是: .
①EF∥AB;②CE∥DF;③∠FDB=2∠CFD;④∠FOE=∠CDF.
三.解答题(共5小题,满分40分)
17.如图,在四边形ABCD中,AD∥BC,∠1=∠2,∠2与∠3互余,以点C为顶点,CD为一边,在四边形ABCD的外部作∠5,使∠5=∠4,交DE于点F,试探索DE和CF的位置关系,并说明理由.
18.如图,AB∥CD,CD平分∠ECF,PD∥CF,在线段CF上取点H,使∠HPF=∠HFP,PQ平分∠EPH.
(1)若∠AEC=30°,求∠EPD的度数;
(2)判断∠QPF与∠AEC的数量关系,说明理由.
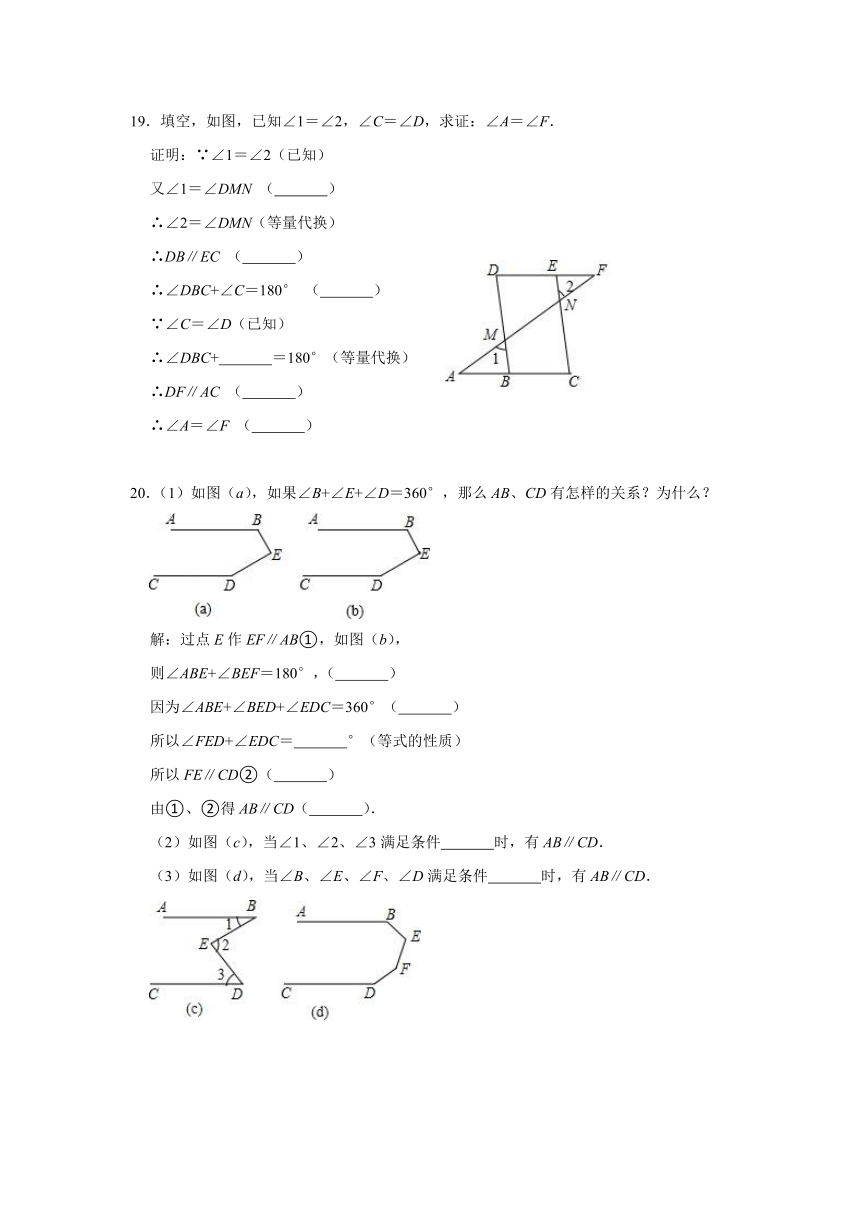
19.填空,如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.
证明:∵∠1=∠2(已知)
又∠1=∠DMN ( )
∴∠2=∠DMN(等量代换)
∴DB∥EC ( )
∴∠DBC+∠C=180° ( )
∵∠C=∠D(已知)
∴∠DBC+ =180°(等量代换)
∴DF∥AC ( )
∴∠A=∠F ( )
20.(1)如图(a),如果∠B+∠E+∠D=360°,那么AB、CD有怎样的关系?为什么?
解:过点E作EF∥AB①,如图(b),
则∠ABE+∠BEF=180°,( )
因为∠ABE+∠BED+∠EDC=360°( )
所以∠FED+∠EDC= °(等式的性质)
所以FE∥CD②( )
由①、②得AB∥CD( ).
(2)如图(c),当∠1、∠2、∠3满足条件 时,有AB∥CD.
(3)如图(d),当∠B、∠E、∠F、∠D满足条件 时,有AB∥CD.
21.如图,点A、B分别在直线CM、DN上,CM∥DN.
(1)如图1,连接AB,则∠CAB+∠ABD= ;
(2)如图2,点P1是直线CM、DN内部的一个点,连接AP1、BP1.求证:∠CAP1+∠AP1B+∠P1BD=360°;
(3)如图3,点P1、P2是直线CM、DN内部的一个点,连接AP1、P1P2、P2B.试求∠CAP1+∠AP1P2+∠P1P2B+∠P2BD的度数;
(4)若按以上规律,猜想并直接写出∠CAP1+∠AP1P2+…∠P5BD的度数(不必写出过程).
参考答案
一.选择题(共8小题,满分40分)
1.解:∵直尺的两边互相平行,
∴∠1=∠2,∠3=∠4,
∵三角板的直角顶点在直尺上,
∴∠2+∠4=90°,
∴A,B,C正确.
故选:D.
2.解:如图所示,过N作NE∥AB,则
∵AB∥CD,
∴AB∥NE∥CD,
∴∠ABN+∠BND+∠CDN=180°×2=360°,
又∵∠BND=160°,
∴∠ABN+∠CDN=200°,
又∵∠MBN=3∠ABM,∠MDN=3∠CDM,
∴∠MBN+∠MDN=×200°=150°,
∴四边形BMDN中,∠M=360°﹣150°﹣160°=50°,
故选:B.
3.解:∵FM平分∠EFD,
∴∠EFM=∠DFM=∠CFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF=∠AEF,
∵EM平分∠BEF,
∴∠BEM=∠FEM=∠BEF,
∴∠GEF+∠FEM=(∠AEF+∠BEF)=90°,即∠GEM=90°,
∠FEM+∠EFM=(∠BEF+∠CFE),
∵AB∥CD,
∴∠EGF=∠AEG,∠CFE=∠AEF
∴∠FEM+∠EFM=(∠BEF+∠CFE)=(BEF+∠AEF)=90°,
∴在△EMF中,∠EMF=90°,
∴∠GEM=∠EMF,
∴EG∥FM,
∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.
故选:C.
4.解:在四边形ABCD中,∠ABD与∠BAC不一定相等,
故①AB∥CD;②△ABD≌△BAC都不一定成立,
∵AC⊥BD,
∴Rt△CDH中,CD2=DH2+CH2;
Rt△ABH中,AB2=AH2+BH2;
Rt△ADH中,AD2=DH2+AH2;
Rt△BCH中,BC2=CH2+BH2;
∴AB2+CD2=AD2+CB2,故③正确;
∵AC⊥BD,
∴∠ABH+∠BAH=90°,
又∵AB=AC=BD,
∴等腰△ABC中,∠ACB=(180°﹣∠BAC),
等腰△ABD中,∠ADB=(180°﹣∠ABD),
∴∠ACB+∠BDA=(180°﹣∠BAC)+(180°﹣∠ABD)
=180°﹣(∠ABH+∠BAH)
=180°﹣45°
=135°,故④正确.
综上所述,真命题的个数是2个,
故选:B.
5.解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=2∠2,设∠2=x,则∠AEF=∠1=∠FEA′=2x,
∴5x=180°,
∴x=36°,
∴∠AEF=2x=72°,
故选:C.
6.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
7.解:如图所示,延长AB交DE于H,
∵BC∥DE,
∴∠ABC=∠AHE=x,
∵CD∥EF,AB∥EG,
∴∠D=∠DEF=z,∠AHE=∠DEG=z+y,
∴∠ABC=∠DEG,即x=z+y,
∴x﹣z=y,
故选:B.
8.解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵直线m∥n,
∴∠1=∠2﹣∠ABC=52°﹣30°=22°.
故答案为:22°.
10.解:∵AB∥CD,∠1=56°,
∴∠3=∠1=56°,
又∵∠2=∠4=56°,
∴∠3=∠4,
∴EF∥GH.
故答案为:EF∥GH.
11.解:分为两种情况:当M在a、b之间时,如在M′点时,直线a和直线b之间的距离是4cm+2cm=6cm;
当M在a、b外时,直线a和直线b之间的距离是4cm﹣2cm=2cm;
故答案为:6cm或2cm.
12.解:如图,∵AB平分∠DAC,EF∥GH,
∴可设∠1=∠2=∠3=α,则∠4=2α,
在△ABC内,∠CBA=180°﹣∠C﹣∠2=60°﹣α,
∵直线BD平分∠FBC,
∴∠6=∠CBF=(∠4+∠C)=(120°+2α)=60°+α,
∴∠DBA=180°﹣∠ABC﹣∠6=180°﹣(60°﹣α)﹣(60°+α)=60°,
故答案为:60°.
13.解:如图,延长CB交ED的延长线于G.
∵AB∥DF,
∴∠1=∠ABC=135°,
∵∠1=∠CDG+∠C,∠CDG=180°﹣∠CDE=110°,
∴∠BCD=135°﹣110°=25°,
故答案为25°.
14.解:过D点作DI∥EF,
∵∠F=150°,
∴∠FDI=30°,
∴∠ADB=180°﹣90°﹣30°﹣35°=25°,
∴∠ABH=90°﹣25°=65°.
∵GH∥AB,
∴∠H=180°﹣65°=115°.
故答案为:115°.
15.解:①∵∠CAB=∠EAD=90°,
∴∠1=∠CAB﹣∠2,∠3=∠EAD﹣∠2,
∴∠1=∠3.
∴①正确.
②∵∠2=30°,
∴∠1=90°﹣30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE.
∴②正确.
③∵∠2=30°,
∴∠3=90°﹣30°=60°,
∵∠B=45°,
∴BC不平行于AD.
∴③错误.
④∵∠2=30°.
∴∠1=60°.
∴∠CAD=∠EAD+∠1=90°+60°=150°.
∴④正确.
综上所述,正确的有①②④.
故答案为:①②④.
16.解:∵∠ACE+∠FDB=180°,
又∠ADF+∠FDB=180°,
∴∠ACE=∠ADF,
∴CE∥DF,
故②符合题意,①不符合题意;
∵CE∥DF,CF平分∠ECB,
∴∠ECF=DFC,∠ECF=∠BCF,
∴∠DFC=∠BCF,
∴∠FDB=∠DFC+∠BCF=2∠CFD,
故③符合题意;
∵EH⊥AB,
∴∠OCH+∠COH=90°,
∴∠FOE=∠COH=90°﹣∠OCH,
又∠CDF=180°﹣(∠DFC+∠DCF)=180°﹣2∠DCF,
∴∠FOE=∠CDF,
故④符合题意.
故答案为:②③④.
三.解答题(共5小题,满分40分)
17.解:DE⊥CF,理由如下:
∵AD∥BC,∠1=∠2,
∴∠1=∠4=∠2,
又∵∠5=∠4,
∴∠5=∠2,
又∵∠2与∠3互余,
∴∠3与∠5互余,
∴∠5+∠3=90°,
∴DE⊥CF.
18.解:(1)∵AB∥CD,
∴∠DCE=∠AEC=30°,
又∵CD平分∠ECF,
∴∠ECF=2∠DCE=60°,
∵PD∥CF,
∴∠EPD=∠ECF=60°;
(2)∵∠HPF=∠HFP,∠CHP是△PHF的外角,
∴∠HPF=∠PHC,
∵PQ平分∠EPH,
∴∠QPH=∠EPH,
∴∠QPF=∠QPH﹣∠FPH
=∠EPH﹣∠PHC
=(∠EPH﹣∠PHC)
=∠ECF
=∠ECD
由AB∥CD可得,∠ECD=∠AEC,
∴∠QPF=∠AEC.
19.证明:∵∠1=∠2(已知)
又∠1=∠DMN (对顶角相等)
∴∠2=∠DMN(等量代换)
∴DB∥EC (同位角相等,两直线平行)
∴∠DBC+∠C=180° (两直线平行,同旁内角互补)
∵∠C=∠D(已知)
∴∠DBC+∠D=180°(等量代换)
∴DF∥AC (同旁内角互补,两直线平行)
∴∠A=∠F (两直线平行,内错角相等)
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;∠D;同旁内角互补,两直线平行;两直线平行,内错角相等.
20.解:(1)
过点E作EF∥AB,如图(b),
则∠ABE+∠BEF=180°,(两直线平行,同旁内角互补)
因为∠ABE+∠BED+∠EDC=360°,(已知 )
所以∠FED+∠EDC=180°,(等式的性质)
所以 FE∥CD,(同旁内角互补,两直线平行)
∴AB∥CD (或平行线的传递性 ).
(2)如图(c),当∠1、∠2、∠3满足条件∠1+∠3=∠2时,有AB∥CD.
理由:过点E作EF∥AB.
∴∠1=∠BEF;
∵∠1+∠3=∠2,∠2=∠BEF+∠DEF,
∴∠3=∠DEF,
∴EF∥CD,
∴AB∥CD(平行线的传递性);
(3)如图(d),当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由:
过点E、F分别作GE∥HF∥CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠E+∠F+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
故答案是:(1)两直线平行,同旁内角互补、已知、180、同旁内角互补,两直线平行或平行线的传递性;
(2)∠1+∠3=∠2;
(3)∠B+∠E+∠F+∠D=540°.
21.解:(1)∵CM∥DN.
∴∠CAB+∠ABD=180°;
(2)点P1作平行于CM和DN的平行线,
∴∠AP1E+∠CAP1=180°,∠EP1B+∠P1BD=180°,
∴∠CAP1+∠AP1B+∠P1BD=∠AP1E+∠CAB+∠EP1B+∠P1BD=180°+180°=360°;
(3)过点P1、P2作平行于CM和DN的平行线,
∴∠AP1E+∠CAP1=180°,∠EP1P2+∠P1P2F=180°,∠FP2B+∠P2BD=180°,
∴∠CAP1+∠AP1P2+∠P1P2B+∠P2BD=∠AP1E+∠CAP1+∠EP1P2+∠P1P2F+∠FP2B+∠P2BD=3×180°=540°;
(4)∠CAP1+∠AP1P2+…∠P5BD=6×180°=1080°.
一.选择题(共8小题,满分40分)
1.直角三角板与两边平行的纸条如图所示放置,下列结论不一定正确的是( )
A.∠1=∠2 B.∠3=∠4 C.∠2+∠4=90° D.∠1=∠4
2.如图,AB∥CD,∠MBN=3∠ABM,∠MDN=3∠CDM,∠N=160°,则∠M为( )
A.45° B.50° C.60° D.65°
3.如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )
A.5 B.6 C.7 D.8
4.如图,在四边形ABCD中,AB=AC=BD,AC与BD相交于H,且AC⊥BD.
①AB∥CD;②△ABD≌△BAC;③AB2+CD2=AD2+CB2;④∠ACB+∠BDA=135°.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
5.如图,ABCD为一长条形纸带,AB∥CD,将ABCD沿EF折叠,A、D两点分别与A′、D′对应,若∠1=2∠2,则∠AEF的度数为( )
A.60° B.65° C.72° D.75°
6.如图,AB∥DE,那么∠BCD=( )
A.180°+∠1﹣∠2 B.∠1+∠2
C.∠2﹣∠1 D.180°+∠2﹣2∠1
7.如图,已知AB∥EG,BC∥DE,CD∥EF,则x、y、z三者之间的关系是( )
A.x+y+z=180° B.x﹣z=y C.y﹣x=z D.y﹣x=x﹣z
8.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
二.填空题(共8小题,满分40分)
9.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置(∠BAC=90°),其中A,B两点分别落在直线m,n上,若∠2=52°,则∠1的度数为 .
10.如图所示,AB∥CD,∠1=56°,∠2=56°,则直线EF与GH的位置关系为 .
11.已知直线a∥b,点M到直线a的距离是4cm,到直线b的距离是2cm,那么直线a和直线b之间的距离为 .
12.已知EF∥GH,A、D为GH上的两点,M、B为EF上的两点,延长AM于点C,AB平分∠DAC,直线DB平分∠FBC,若∠ACB=120°,则∠DBA的度数 .
13.如图,已知AB∥DE,∠ABC=135°,∠CDE=70°,则∠BCD= .
14.如图,放置在水平操场上的篮球架的横梁EF始终平行于AB,EF与上拉杆CF形成的∠F=150°,主柱AD垂直于地面,通过调整CF和后拉杆BC的位置来调整篮筐的高度.当∠CDB=35°时,点H,D,B在同一直线上,则∠H的度数是 .
15.若将一副三角板按如图放置,下列结论:①∠1=∠3;②若∠2=30°,则AC∥DE;③若∠2=30°,则BC∥AD;④若∠2=30°,则∠CAD=150°.其中正确的序号有 .
16.如图:已知点C、D是直线AB上两点,点E,F为平面内两点,且∠ACE+∠FDB=180°,CF平分∠ECB,EH⊥AB于点H交CF于点O.则下列结论正确的是: .
①EF∥AB;②CE∥DF;③∠FDB=2∠CFD;④∠FOE=∠CDF.
三.解答题(共5小题,满分40分)
17.如图,在四边形ABCD中,AD∥BC,∠1=∠2,∠2与∠3互余,以点C为顶点,CD为一边,在四边形ABCD的外部作∠5,使∠5=∠4,交DE于点F,试探索DE和CF的位置关系,并说明理由.
18.如图,AB∥CD,CD平分∠ECF,PD∥CF,在线段CF上取点H,使∠HPF=∠HFP,PQ平分∠EPH.
(1)若∠AEC=30°,求∠EPD的度数;
(2)判断∠QPF与∠AEC的数量关系,说明理由.
19.填空,如图,已知∠1=∠2,∠C=∠D,求证:∠A=∠F.
证明:∵∠1=∠2(已知)
又∠1=∠DMN ( )
∴∠2=∠DMN(等量代换)
∴DB∥EC ( )
∴∠DBC+∠C=180° ( )
∵∠C=∠D(已知)
∴∠DBC+ =180°(等量代换)
∴DF∥AC ( )
∴∠A=∠F ( )
20.(1)如图(a),如果∠B+∠E+∠D=360°,那么AB、CD有怎样的关系?为什么?
解:过点E作EF∥AB①,如图(b),
则∠ABE+∠BEF=180°,( )
因为∠ABE+∠BED+∠EDC=360°( )
所以∠FED+∠EDC= °(等式的性质)
所以FE∥CD②( )
由①、②得AB∥CD( ).
(2)如图(c),当∠1、∠2、∠3满足条件 时,有AB∥CD.
(3)如图(d),当∠B、∠E、∠F、∠D满足条件 时,有AB∥CD.
21.如图,点A、B分别在直线CM、DN上,CM∥DN.
(1)如图1,连接AB,则∠CAB+∠ABD= ;
(2)如图2,点P1是直线CM、DN内部的一个点,连接AP1、BP1.求证:∠CAP1+∠AP1B+∠P1BD=360°;
(3)如图3,点P1、P2是直线CM、DN内部的一个点,连接AP1、P1P2、P2B.试求∠CAP1+∠AP1P2+∠P1P2B+∠P2BD的度数;
(4)若按以上规律,猜想并直接写出∠CAP1+∠AP1P2+…∠P5BD的度数(不必写出过程).
参考答案
一.选择题(共8小题,满分40分)
1.解:∵直尺的两边互相平行,
∴∠1=∠2,∠3=∠4,
∵三角板的直角顶点在直尺上,
∴∠2+∠4=90°,
∴A,B,C正确.
故选:D.
2.解:如图所示,过N作NE∥AB,则
∵AB∥CD,
∴AB∥NE∥CD,
∴∠ABN+∠BND+∠CDN=180°×2=360°,
又∵∠BND=160°,
∴∠ABN+∠CDN=200°,
又∵∠MBN=3∠ABM,∠MDN=3∠CDM,
∴∠MBN+∠MDN=×200°=150°,
∴四边形BMDN中,∠M=360°﹣150°﹣160°=50°,
故选:B.
3.解:∵FM平分∠EFD,
∴∠EFM=∠DFM=∠CFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF=∠AEF,
∵EM平分∠BEF,
∴∠BEM=∠FEM=∠BEF,
∴∠GEF+∠FEM=(∠AEF+∠BEF)=90°,即∠GEM=90°,
∠FEM+∠EFM=(∠BEF+∠CFE),
∵AB∥CD,
∴∠EGF=∠AEG,∠CFE=∠AEF
∴∠FEM+∠EFM=(∠BEF+∠CFE)=(BEF+∠AEF)=90°,
∴在△EMF中,∠EMF=90°,
∴∠GEM=∠EMF,
∴EG∥FM,
∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.
故选:C.
4.解:在四边形ABCD中,∠ABD与∠BAC不一定相等,
故①AB∥CD;②△ABD≌△BAC都不一定成立,
∵AC⊥BD,
∴Rt△CDH中,CD2=DH2+CH2;
Rt△ABH中,AB2=AH2+BH2;
Rt△ADH中,AD2=DH2+AH2;
Rt△BCH中,BC2=CH2+BH2;
∴AB2+CD2=AD2+CB2,故③正确;
∵AC⊥BD,
∴∠ABH+∠BAH=90°,
又∵AB=AC=BD,
∴等腰△ABC中,∠ACB=(180°﹣∠BAC),
等腰△ABD中,∠ADB=(180°﹣∠ABD),
∴∠ACB+∠BDA=(180°﹣∠BAC)+(180°﹣∠ABD)
=180°﹣(∠ABH+∠BAH)
=180°﹣45°
=135°,故④正确.
综上所述,真命题的个数是2个,
故选:B.
5.解:由翻折的性质可知:∠AEF=∠FEA′,
∵AB∥CD,
∴∠AEF=∠1,
∵∠1=2∠2,设∠2=x,则∠AEF=∠1=∠FEA′=2x,
∴5x=180°,
∴x=36°,
∴∠AEF=2x=72°,
故选:C.
6.解:过点C作CF∥AB,如图:
∵AB∥DE,
∴AB∥DE∥CF,
∴∠BCF=∠1①,∠2+∠DCF=180°②,
∴①+②得,∠BCF+∠DCF+∠2=∠1+180°,即∠BCD=180°+∠1﹣∠2.
故选:A.
7.解:如图所示,延长AB交DE于H,
∵BC∥DE,
∴∠ABC=∠AHE=x,
∵CD∥EF,AB∥EG,
∴∠D=∠DEF=z,∠AHE=∠DEG=z+y,
∴∠ABC=∠DEG,即x=z+y,
∴x﹣z=y,
故选:B.
8.解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
二.填空题(共8小题,满分40分)
9.解:∵直线m∥n,
∴∠1=∠2﹣∠ABC=52°﹣30°=22°.
故答案为:22°.
10.解:∵AB∥CD,∠1=56°,
∴∠3=∠1=56°,
又∵∠2=∠4=56°,
∴∠3=∠4,
∴EF∥GH.
故答案为:EF∥GH.
11.解:分为两种情况:当M在a、b之间时,如在M′点时,直线a和直线b之间的距离是4cm+2cm=6cm;
当M在a、b外时,直线a和直线b之间的距离是4cm﹣2cm=2cm;
故答案为:6cm或2cm.
12.解:如图,∵AB平分∠DAC,EF∥GH,
∴可设∠1=∠2=∠3=α,则∠4=2α,
在△ABC内,∠CBA=180°﹣∠C﹣∠2=60°﹣α,
∵直线BD平分∠FBC,
∴∠6=∠CBF=(∠4+∠C)=(120°+2α)=60°+α,
∴∠DBA=180°﹣∠ABC﹣∠6=180°﹣(60°﹣α)﹣(60°+α)=60°,
故答案为:60°.
13.解:如图,延长CB交ED的延长线于G.
∵AB∥DF,
∴∠1=∠ABC=135°,
∵∠1=∠CDG+∠C,∠CDG=180°﹣∠CDE=110°,
∴∠BCD=135°﹣110°=25°,
故答案为25°.
14.解:过D点作DI∥EF,
∵∠F=150°,
∴∠FDI=30°,
∴∠ADB=180°﹣90°﹣30°﹣35°=25°,
∴∠ABH=90°﹣25°=65°.
∵GH∥AB,
∴∠H=180°﹣65°=115°.
故答案为:115°.
15.解:①∵∠CAB=∠EAD=90°,
∴∠1=∠CAB﹣∠2,∠3=∠EAD﹣∠2,
∴∠1=∠3.
∴①正确.
②∵∠2=30°,
∴∠1=90°﹣30°=60°,
∵∠E=60°,
∴∠1=∠E,
∴AC∥DE.
∴②正确.
③∵∠2=30°,
∴∠3=90°﹣30°=60°,
∵∠B=45°,
∴BC不平行于AD.
∴③错误.
④∵∠2=30°.
∴∠1=60°.
∴∠CAD=∠EAD+∠1=90°+60°=150°.
∴④正确.
综上所述,正确的有①②④.
故答案为:①②④.
16.解:∵∠ACE+∠FDB=180°,
又∠ADF+∠FDB=180°,
∴∠ACE=∠ADF,
∴CE∥DF,
故②符合题意,①不符合题意;
∵CE∥DF,CF平分∠ECB,
∴∠ECF=DFC,∠ECF=∠BCF,
∴∠DFC=∠BCF,
∴∠FDB=∠DFC+∠BCF=2∠CFD,
故③符合题意;
∵EH⊥AB,
∴∠OCH+∠COH=90°,
∴∠FOE=∠COH=90°﹣∠OCH,
又∠CDF=180°﹣(∠DFC+∠DCF)=180°﹣2∠DCF,
∴∠FOE=∠CDF,
故④符合题意.
故答案为:②③④.
三.解答题(共5小题,满分40分)
17.解:DE⊥CF,理由如下:
∵AD∥BC,∠1=∠2,
∴∠1=∠4=∠2,
又∵∠5=∠4,
∴∠5=∠2,
又∵∠2与∠3互余,
∴∠3与∠5互余,
∴∠5+∠3=90°,
∴DE⊥CF.
18.解:(1)∵AB∥CD,
∴∠DCE=∠AEC=30°,
又∵CD平分∠ECF,
∴∠ECF=2∠DCE=60°,
∵PD∥CF,
∴∠EPD=∠ECF=60°;
(2)∵∠HPF=∠HFP,∠CHP是△PHF的外角,
∴∠HPF=∠PHC,
∵PQ平分∠EPH,
∴∠QPH=∠EPH,
∴∠QPF=∠QPH﹣∠FPH
=∠EPH﹣∠PHC
=(∠EPH﹣∠PHC)
=∠ECF
=∠ECD
由AB∥CD可得,∠ECD=∠AEC,
∴∠QPF=∠AEC.
19.证明:∵∠1=∠2(已知)
又∠1=∠DMN (对顶角相等)
∴∠2=∠DMN(等量代换)
∴DB∥EC (同位角相等,两直线平行)
∴∠DBC+∠C=180° (两直线平行,同旁内角互补)
∵∠C=∠D(已知)
∴∠DBC+∠D=180°(等量代换)
∴DF∥AC (同旁内角互补,两直线平行)
∴∠A=∠F (两直线平行,内错角相等)
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,同旁内角互补;∠D;同旁内角互补,两直线平行;两直线平行,内错角相等.
20.解:(1)
过点E作EF∥AB,如图(b),
则∠ABE+∠BEF=180°,(两直线平行,同旁内角互补)
因为∠ABE+∠BED+∠EDC=360°,(已知 )
所以∠FED+∠EDC=180°,(等式的性质)
所以 FE∥CD,(同旁内角互补,两直线平行)
∴AB∥CD (或平行线的传递性 ).
(2)如图(c),当∠1、∠2、∠3满足条件∠1+∠3=∠2时,有AB∥CD.
理由:过点E作EF∥AB.
∴∠1=∠BEF;
∵∠1+∠3=∠2,∠2=∠BEF+∠DEF,
∴∠3=∠DEF,
∴EF∥CD,
∴AB∥CD(平行线的传递性);
(3)如图(d),当∠B、∠E、∠F、∠D满足条件∠B+∠E+∠F+∠D=540°时,有AB∥CD.
理由:
过点E、F分别作GE∥HF∥CD.
则∠GEF+∠EFH=180°,∠HFD+∠CDF=180°,
∴∠GEF+∠EFD+∠FDC=360°;
又∵∠B+∠E+∠F+∠D=540°,
∴∠ABE+∠BEG=180°,
∴AB∥GE,
∴AB∥CD;
故答案是:(1)两直线平行,同旁内角互补、已知、180、同旁内角互补,两直线平行或平行线的传递性;
(2)∠1+∠3=∠2;
(3)∠B+∠E+∠F+∠D=540°.
21.解:(1)∵CM∥DN.
∴∠CAB+∠ABD=180°;
(2)点P1作平行于CM和DN的平行线,
∴∠AP1E+∠CAP1=180°,∠EP1B+∠P1BD=180°,
∴∠CAP1+∠AP1B+∠P1BD=∠AP1E+∠CAB+∠EP1B+∠P1BD=180°+180°=360°;
(3)过点P1、P2作平行于CM和DN的平行线,
∴∠AP1E+∠CAP1=180°,∠EP1P2+∠P1P2F=180°,∠FP2B+∠P2BD=180°,
∴∠CAP1+∠AP1P2+∠P1P2B+∠P2BD=∠AP1E+∠CAP1+∠EP1P2+∠P1P2F+∠FP2B+∠P2BD=3×180°=540°;
(4)∠CAP1+∠AP1P2+…∠P5BD=6×180°=1080°.
