人教A版(2019)必修第一册必杀技第四章4.5.3函数模型的应用(word版含解析)
文档属性
| 名称 | 人教A版(2019)必修第一册必杀技第四章4.5.3函数模型的应用(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 801.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 13:09:20 | ||
图片预览




文档简介
人教A版(2019)必修第一册必杀技第四章4.5.3函数模型的应用
一、单选题
1.设集合,,则( )
A.
B.
C.
D.
2.正三棱柱的底面边长为,侧棱长为,为的中点,则与平面所成角的正弦值为( )
A. B. C. D.
3.已知点A(1,3)、B(3,1)、C(-1,0),则△ABC的面积等于 ( )
A.3 B.4 C.5 D.6
4.若f(x)=,则f(–2)的值为
A.0 B.1 C.2 D.–2
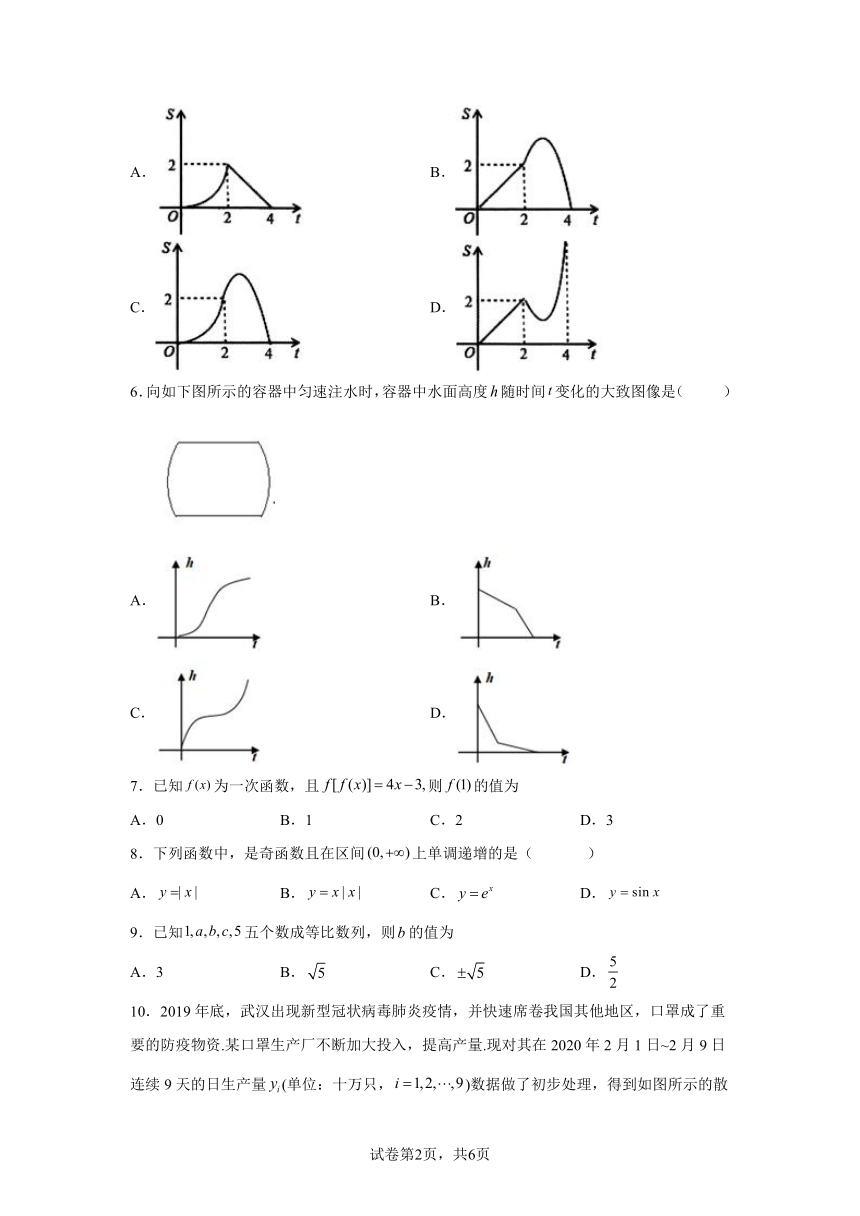
5.如图,直线l的解析式为y=-x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是
A. B.
C. D.
6.向如下图所示的容器中匀速注水时,容器中水面高度随时间变化的大致图像是( )
A. B.
C. D.
7.已知为一次函数,且则的值为
A.0 B.1 C.2 D.3
8.下列函数中,是奇函数且在区间上单调递增的是( )
A. B. C. D.
9.已知五个数成等比数列,则的值为
A.3 B. C. D.
10.2019年底,武汉出现新型冠状病毒肺炎疫情,并快速席卷我国其他地区,口罩成了重要的防疫物资.某口罩生产厂不断加大投入,提高产量.现对其在2020年2月1日~2月9日连续9天的日生产量(单位:十万只,)数据做了初步处理,得到如图所示的散点图.那么不可能作为关于的回归方程类型的是( )
A. B.
C. D.
11.我国工农业总产值从年到年的年间翻了两番,设平均每年的增长率为,则有( )
A. B.
C. D.
12.若某商店将进货单价为元的商品按每件元出售.则每天可销售件.现准备采用提高售价、减少进货量的方法来增加利润.己知这种商品的售价每提高元,销售量就要减少件,那么要保证该商品每天的利润在元以上,售价应定为( )
A.元 B.元到元之间 C.元 D.元到元之间
13.某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系(为自然对数的底数,,为常数).若该食品在的保鲜时间是144小时,在的保鲜时间是36小时,则该食品在的保鲜时间是( )
A.16小时 B.18小时 C.20小时 D.24小时
14.已知函数在上单调递增,则实数的取值范围是( )
A. B. C. D.
15.建造一个容积为2m,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为
A.660 B.760 C.670 D.680
16.某种产品平均每三年降低价格25%,目前售价为640元,则9年后此产品的价格为
A.210 B.240 C.270 D.360
二、双空题
17.若将时钟拨慢5分钟,则分针转了________弧度,时针转了________度.
18.已知函数,则______;若,则实数______.
三、填空题
19.设函数,则________.
20.已知函数与的图象上存在关于轴对称的点,则实数的取值范围是_________.
21.我国古代有一则家喻户晓的神话故事——后羿射日,在《淮南子 本经训》和《山海经 海内经》都有一定记载.如果被射下来的九个太阳中有一个距离地球约3500光年,如果将“3500光年”的单位“光年”换算成以”米”为单位,所得结果的数量级是___________(光年是指光在宇宙真空中沿直线经过一年时间的距离,光速;通常情况下,数量级是指一系列10的幂,例如数字的数量级是3).
22.___________.
23.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品万件时的生产成本为 (万元).一万件售价为万元,为获取更大利润,该企业一个月应生产该商品数量为________万件.
24.已知函数f(x)满足:f(x+y)=f(x)f(y),且当x>y时,f(x)>f(y),请你写出符合上述条件的一个函数f(x)=_______.
四、解答题
25.已知A,B,C是函数图象上的三点,它们的横坐标依次为t,t+2,t+4,其中e=2.71828…为自然对数的底数
(1)求△ABC面积S关于的函数关系式S=g(t);
(2)用单调性的定义证明函数在[0,+∞)上是增函数
26.已知2016年我国国内生产总值为a,设以后每年的年平均增长率为b,试写出x年后国内生产总值y和x之间的函数关系式.
27.已知,,分别是的三个内角,,的对边,且.
(1)求角的值;
(2)若,边上的中线的长为,求.
28.已知函数.
(1)若函数为偶函数,求实数的值;
(2)若,且函数在上单调,求实数的值;
(3)令,若当时,总有,使得,求实数的取值范围.
29.如图,一座小岛距离海岸线上最近的点P的距离是3 km,从点P沿海岸正东12 km处有一个渔村.
(1)假设一个人驾驶的小船的平均速度为,步行的速度是.y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
(2)在(1)的条件下,是否有一个停船的位置使得从小岛到渔村花费的时间最少 说明理由.()
30.一片森林原来面积为2014万亩,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐的面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
31.2013年9月22日,为应对台风“天兔”侵袭,我校食堂做好了充分准备,储备了至少三天的食物,食物在储藏时,有些易于保存,而有些却需要适当处理,如牛奶等,它们的保鲜时间会因储藏时温度的不同而不同,假定保鲜时间与储藏温度间的关系为指数型函数(且),若牛奶放在0℃的冰箱中,保鲜时间约为192时,放在22℃的厨房中,保鲜时间约为42时.
(1)写出保鲜时间(单位:时)关于储藏温度(单位:℃)的函数解析式;
(2)请运用(1)的结论计算,若我校购买的牛奶至少要储藏三天,则储藏时的温度最高约为多少?(精确到整数).(参考数据:)
32.某汽车租赁公司的月收益y(单位:元)与每辆车的月租金x(单位:元)间的关系为,那么,每辆车的月租金为多少元时,租赁公司的月收益最大?最大月收益是多少?
试卷第页,共页
试卷第页,共页
参考答案:
1.C
【解析】
【分析】
先利用补集运算求得B的补集,再利用交集运算求解.
【详解】
因为,
所以,
又,
所以,
故选:C.
2.A
【解析】
【分析】
取的中点,连结,则,则与平面所成角可转化为与平面所成角,过点作于点,则是与平面所成角,由此能求出与平面所成角的正弦值.
【详解】
取的中点,连结,则,
则与平面所成角可转化为与平面所成角,
过点作于点,
由于是正三棱柱,
平面平面,
平面,
是与平面所成角,
由题意,,
,
在中,,
与平面所成角的正弦值为.
故选:A
【点睛】
本题考查了线面角的求法,解题的关键是作出线面角,考查了考生的空间想象能力,属于基础题.
3.C
【解析】
【详解】
设AB边上的高为h,则S△ABC=|AB|·h.|AB|= ,AB边上的高h就是点C到直线AB的距离.AB边所在的直线方程为,即x+y-4=0.点C到直线x+y-4=0的距离为,因此,S△ABC=×2 ×=5.
4.B
【解析】
【分析】
利用函数的解析式知道当x<1时是以2周期的周期函数,故f(﹣2)=f(2),再代入函数解析式即得
【详解】
∵f(x)=,x=–2<1,∴f(–2)=f(0)=f(2),∵x=2>1,∴f(2)=log22=1,故选B.
5.C
【解析】
【分析】
分别计算出和时, S与t之间的函数关系,再结合四个选项即可判断出答案.
【详解】
当时,,
当时,,
分析四个选项可知,选C.
故选:C
【点睛】
本题考查了求分段函数的解析式,考查了函数的图象的识别,属于基础题.
6.C
【解析】
【分析】
因为容器中间凸,所以匀速注水时,开始和结束时水位高度变化快中间时水位高度变化慢,可知选C.
【详解】
结合容器的形状,可知一开始注水时,水高度变化较快当水位接近中部时变慢并持续一段时间,接近上部时,水位高度变快,故选C.
【点睛】
本题主要考查了对函数概念的理解及函数图象的认识,结合生活实践,属于中档题.
7.B
【解析】
【分析】
设,代入得到或,计算得到答案.
【详解】
设
则
或
综上:
故答案选B
【点睛】
本题考查了一次函数的计算,待定系数法是常规方法,需要灵活掌握和应用.
8.B
【解析】
根据题意,依次分析选项中函数的奇偶性与单调性,综合即可得答案.
【详解】
解:根据题意,依次分析选项:
对于A, ,为偶函数,不符合题意;
对于B,,为奇函数,当时,在上单调递增,符合题意;
对于C,为指数函数,不是奇函数,不符合题意;
对于D,为正弦函数,在区间上不是单调函数,不符合题意;
故选:B.
【点睛】
本题考查函数的奇偶性与单调性的判定,关键是掌握常见函数的奇偶性与单调性,属于基础题.
9.B
【解析】
【详解】
试题分析:由题意得,,又,所以,故选B.
考点:等比数列的性质.
10.D
【解析】
【分析】
利用导数的几何意义和导数的单调性判断.
【详解】
对于A,,则,若函数为增函数,则,随着的增大,减小,故满足条件;
对于B,,则,若函数为增函数,则,随着的增大,减小,故满足条件;
对于C,,则,若函数为增函数,则,随着的增大,减小,故满足条件;
对于D,,则,若函数为增函数,则,随着的增大,增大,不满足条件.
故选:D.
11.D
【解析】
【分析】
设的总产值为,我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的倍,然后根据平均增长率的定义列等式即可.
【详解】
本题为增长率模型函数,为指数函数形式.
设年总产值为,由于我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的,则.
故选D.
【点睛】
本题考查平均增长律的定义,根据题意列式是解本题的关键,考查分析问题和解决问题的能力,属于基础题.
12.B
【解析】
【分析】
由题意列出关系式,并解不等式.
【详解】
设售价为,利润为,
则,
由题意,
即,
解得,
即售价应定为元到元之间,
故选:B.
13.B
【解析】
【分析】
根据保鲜时间与储藏温度满足函数关系:,并结合食品在的保鲜时间是144小时,在的保鲜时间是36小时,可求出,然后再将代入,即可得出答案.
【详解】
解:由题可知,保鲜时间与储藏温度满足函数关系:,
则,即,所以,
于是当时,=18(小时).
故选:B.
14.B
【解析】
根据函数在上单调递增,则对称轴求解.
【详解】
因为函数在上单调递增,
所以,
解得.
故选:B
【点睛】
本题主要考查二次函数的单调性的应用,属于基础题.
15.B
【解析】
【详解】
试题分析:依题意可知长方体底面面积为1.
设长方体底面一边长为,则底面另一边长为.
设水池总造价为元,
则
即,当且仅当即时取等号.
故B正确.
考点:1函数解析式;2基本不等式.
16.C
【解析】
【详解】
试题分析:由已知中某种产品平均每三年降低价格25%,目前售价为640元,我们易得9年后此产品共降价3次,代入计算即可得到答案:∵产品平均每三年降低价格25%,故9年后此产品共降价3次,又∵目前售价为640元,∴9年后此产品的价格为640×(1-25%)3=270元,故选C.
考点:本试题主要考查了是函数模型的选择与应用,指数的运算.
点评:其中根据已知判断出9年后此产品共降价3次,是解答本题的关键.
17. 2.5
【解析】
【分析】
利用分针逆时针转一周为60分钟,转过的角度为2π,得到10分钟是一周的六分之一,可得分针转的弧度.推导出1分钟时针逆时针转动0.5°,由此能求出将时钟慢5分钟,时针转动的角的大小.
【详解】
将时钟拨慢5分钟,分针、时针都是按逆时针方向转动,转过的角都是正角,这时,分针转过的角度是,即(弧度),时针转过的角度是.
故答案为,2.5.
【点睛】
本题考查弧度的定义,一周对的角是2π弧度.考查逆时针旋转得到的角是正角.注意任意角定义的合理运用.
18. 0 -3
【解析】
(1)先求f(3)的值,再求的值得解;(2)对a分类讨论解方程得解.
【详解】
(1)由题得f(3),所以.
(2)当a<0时,或,因为a<0,所以;
当a≥0时,,显然无实数解.
所以.
故答案为:(1)0;(2)-3.
【点睛】
本题主要考查分段函数的求值和应用,意在考查学生对这些知识的理解掌握水平.
19.6
【解析】
【分析】
根据分段函数的定义,分别求出和,计算即可求出结果.
【详解】
由题知,,
,
.
故答案为:6.
【点睛】
本题考查了分段函数求函数值的问题,考查了对数的运算.属于基础题.
20.
【解析】
【分析】
函数f(x)与g(x)图象上存在关于y轴对称的点,就是f(﹣x)=g(x)有解,也就是函数y=f(﹣x)与函数y=g(x)有交点,
在同一坐标系内画函数y=f(﹣x)(x>0)与函数y=g(x)=ln(x+a)的图象,结合图象解题.
【详解】
函数f(x)与g(x)图象上存在关于y轴有对称的点,
就是f(﹣x)=g(x)有解,
也就是函数y=f(﹣x)与函数y=g(x)有交点,
在同一坐标系内画函数y=f(﹣x)(x>0)与函数y=g(x)=ln(x+a)的图象:
∴函数y=g(x)=ln(x+a)的图象是把由函数y=lnx的图象向左平移
且平移到过点(0,)后开始,两函数的图象没有有交点,
把点(0,)代入y=ln(x+a)得,lna,∴a,
∴a,
故答案为:.
【点睛】
本题主要考查函数的图象,把方程的根的问题转化为函数图象的交点问题,体现了数形结合的思想.
21.19
【解析】
【分析】
根据题意得到距离地球约3500光年,一年走过的路程为,3500光年走过的路程为计算出结果即可.
【详解】
根据题意得到距离地球约3500光年,一年有秒,光速,
一年走过的路程为
3500光年走过的路程为
数量级为19.
故答案为:19.
22.6
【解析】
【分析】
利用对数运算求解.
【详解】
,
故答案为:6
23.
【解析】
根据题意,可得利润=售价-成本,将利润表示出来,得到关于的二次函数,再根据二次函数性质求解最大值即可.
【详解】
设利润为,则,当时,有最大值,
故答案为:18.
【点睛】
本题是函数的应用题,关键是建立函数的关系式求解,解函数应用题,一般可按照以下步骤进行:
(1)读题:读懂和深刻理解题意,找出等量关系,将应用问题转化为数学问题;
(2)建模:把主要关系近似化、形式化,抽象成数学问题;
(3)求解:化归为常规问题,选择合适的数学方法求解;
(4)评价:对结果进行验证或评估,对错误加以调节,最终将结果应用于现实.
24.(答案不唯一)
【解析】
【分析】
由f(x+y)=f(x)f(y),可得指数函数具有此性质,从而可得函数
【详解】
对于函数,
,
且当x>y时,f(x)>f(y),
所以函数满足条件,
故答案为:(答案不唯一)
25.(1);(2)见解析
【解析】
【分析】
(1)通过面积作差法求出函数的S=g(t)的解析式;
(2)根据函数单调性的定义证明函数的单调性即可.
【详解】
(1)由题意,可知
(2)由(1),知.
考虑函数,任取,且,则
因为,所以,,从而,,
因此.
故在上是增函数,注意到,所以在上是增函数.
【点睛】
本题考查了函数的单调性问题,考查求函数的解析式,是一道中档题
证明函数的单调性用定义法的步骤:①取值;②作差;③变形;④确定符号;⑤下结论
26.
【解析】
【分析】
由每年国内生产总值是上一年的倍得出函数关系式.
【详解】
因为每年的年平均增长率为b,所以年开始,每年国内生产总值是上一年的倍,所以x年后国内生产总值
27.(1);(2)
【解析】
【分析】
(1)利用正弦定理,结合和角的正弦公式,即可求角A的值:
(2)若AB=3,AC边上的中线BD的长为,求出AC,再求△ABC的面积.
【详解】
(1)由及正弦定理得:,
即,
即,
即,
因为,所以,则,又,所以.
(2)在中,,,,由余弦定理得
,所以,所以(负值舍去),
又为中点,所以.
【点睛】
本题考查正弦定理、余弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.
28.(1);(2);(3).
【解析】
【分析】
(1)根据偶函数图象关于轴对称,二次函数的一次项系数为0,可得的值;
(2)根据,可知时,取得最大值,且在,上是单调函数,即,即可求解实数的值.
(3)求解的值域和的值域,可得,即可求解实数的取值范围.
【详解】
(1)函数,为偶函数,
可得,
可得
即实数的值为;
(2)由,可知时,取得最大值,
即,
可得:
且在,上是单调函数,
,即
可得:.
当时,可得,
故得实数的值为.
(3)由,可得.
,,
,,
那么的值域,.
当,时,总有,,使得转化为函数的值域是的值域的子集;
即:当,时,
函数,
其对称轴,开口向下,
当时,即,可得(2);;
可得解:
当时,即可得;或;
此时无解.
当时,即,可得;(2);
此时无解.
综上可得实数的取值范围为,.
29.(1),;(2)当停船位置距离点约时,从小岛到渔村花费的时间最少;理由见解析
【解析】
【分析】
(1)利用路程除以速度可得时间,从而构造出函数关系式;
(2)利用定义法可证得函数在上单调递减,在上单调递增;由此可得当时,所花费时间最少.
【详解】
(1)由题意得:小岛距离点的距离为
一个人从小岛到处所需时间为,从处到渔村所需时间为
,
(2)当时,
,
函数在上单调递减
同理可得:函数在上单调递增
当时,()
当停船位置距离点约时,从小岛到渔村花费的时间最少
【点睛】
本题考查构造函数模型求解实际问题,涉及到最值问题的求解;求解最值问题的关键是能够判断出函数的单调区间,进而根据单调性得到最值点.
30.(1);(2)5;(3)15.
【解析】
【分析】
(1)设每年砍伐面积的百分比为,由指数函数的性质列式求解;
(2)由求解可得;
(3)由求解可得.
【详解】
(1)设每年砍伐面积的百分比为,则,解得;
(2)设到今年为止,该森林已砍伐了年,则,
,,;
(3)设今后最多还能砍伐年,
则,
,,.
答:(1)每年砍伐面积的百分比为;(2)到今年为止,该森林已砍伐了5年;(3)今后最多还能砍伐15年.
【点睛】
思路点睛:本题考查指数函数的应用,解题关键是根据每年砍伐的百分比相同,设百分比为,那么年后,剩余量为.抓住这个模型,通过解指数方程、指数不等式可得.
31.(1);(2)14℃.
【解析】
【分析】
(1)运用代入法进行求解即可;
(2)由(1)的函数解析式,根据题意得到不等式,利用换底公式进行求解即可.
【详解】
(1)设(且),则有,,.
(2)依题意有,
若我校购买的牛奶至少要储藏三天,则储藏时的温度最高约为14℃.
32.4050元,最大月收益307050元
【解析】
将函数化为顶点式,由二次函数的性质即可得出结论.
【详解】
解:,∴当时,.即每辆车的月租金为4050元时,租赁公司的月收益最大,最大月收益是307050元.
【点睛】
本题主要考查了二次函数模型解决实际问题,属于中等题.
试卷第页,共页
试卷第页,共页
一、单选题
1.设集合,,则( )
A.
B.
C.
D.
2.正三棱柱的底面边长为,侧棱长为,为的中点,则与平面所成角的正弦值为( )
A. B. C. D.
3.已知点A(1,3)、B(3,1)、C(-1,0),则△ABC的面积等于 ( )
A.3 B.4 C.5 D.6
4.若f(x)=,则f(–2)的值为
A.0 B.1 C.2 D.–2
5.如图,直线l的解析式为y=-x+4,它与x轴和y轴分别相交于A,B两点.平行于直线l的直线m从原点O出发,沿x轴的正方向以每秒1个单位长度的速度运动.它与x轴和y轴分别相交于C,D两点,运动时间为t秒(0≤t≤4),以CD为斜边作等腰直角三角形CDE(E,O两点分别在CD两侧).若△CDE和△OAB的重合部分的面积为S,则S与t之间的函数关系的图象大致是
A. B.
C. D.
6.向如下图所示的容器中匀速注水时,容器中水面高度随时间变化的大致图像是( )
A. B.
C. D.
7.已知为一次函数,且则的值为
A.0 B.1 C.2 D.3
8.下列函数中,是奇函数且在区间上单调递增的是( )
A. B. C. D.
9.已知五个数成等比数列,则的值为
A.3 B. C. D.
10.2019年底,武汉出现新型冠状病毒肺炎疫情,并快速席卷我国其他地区,口罩成了重要的防疫物资.某口罩生产厂不断加大投入,提高产量.现对其在2020年2月1日~2月9日连续9天的日生产量(单位:十万只,)数据做了初步处理,得到如图所示的散点图.那么不可能作为关于的回归方程类型的是( )
A. B.
C. D.
11.我国工农业总产值从年到年的年间翻了两番,设平均每年的增长率为,则有( )
A. B.
C. D.
12.若某商店将进货单价为元的商品按每件元出售.则每天可销售件.现准备采用提高售价、减少进货量的方法来增加利润.己知这种商品的售价每提高元,销售量就要减少件,那么要保证该商品每天的利润在元以上,售价应定为( )
A.元 B.元到元之间 C.元 D.元到元之间
13.某食品的保鲜时间(单位:小时)与储藏温度(单位:)满足函数关系(为自然对数的底数,,为常数).若该食品在的保鲜时间是144小时,在的保鲜时间是36小时,则该食品在的保鲜时间是( )
A.16小时 B.18小时 C.20小时 D.24小时
14.已知函数在上单调递增,则实数的取值范围是( )
A. B. C. D.
15.建造一个容积为2m,深为2m的长方体无盖水池,如果池底和池壁的造价每平方米分别为120元和80元,则水池的最低造价为
A.660 B.760 C.670 D.680
16.某种产品平均每三年降低价格25%,目前售价为640元,则9年后此产品的价格为
A.210 B.240 C.270 D.360
二、双空题
17.若将时钟拨慢5分钟,则分针转了________弧度,时针转了________度.
18.已知函数,则______;若,则实数______.
三、填空题
19.设函数,则________.
20.已知函数与的图象上存在关于轴对称的点,则实数的取值范围是_________.
21.我国古代有一则家喻户晓的神话故事——后羿射日,在《淮南子 本经训》和《山海经 海内经》都有一定记载.如果被射下来的九个太阳中有一个距离地球约3500光年,如果将“3500光年”的单位“光年”换算成以”米”为单位,所得结果的数量级是___________(光年是指光在宇宙真空中沿直线经过一年时间的距离,光速;通常情况下,数量级是指一系列10的幂,例如数字的数量级是3).
22.___________.
23.生产一定数量的商品的全部费用称为生产成本,某企业一个月生产某种商品万件时的生产成本为 (万元).一万件售价为万元,为获取更大利润,该企业一个月应生产该商品数量为________万件.
24.已知函数f(x)满足:f(x+y)=f(x)f(y),且当x>y时,f(x)>f(y),请你写出符合上述条件的一个函数f(x)=_______.
四、解答题
25.已知A,B,C是函数图象上的三点,它们的横坐标依次为t,t+2,t+4,其中e=2.71828…为自然对数的底数
(1)求△ABC面积S关于的函数关系式S=g(t);
(2)用单调性的定义证明函数在[0,+∞)上是增函数
26.已知2016年我国国内生产总值为a,设以后每年的年平均增长率为b,试写出x年后国内生产总值y和x之间的函数关系式.
27.已知,,分别是的三个内角,,的对边,且.
(1)求角的值;
(2)若,边上的中线的长为,求.
28.已知函数.
(1)若函数为偶函数,求实数的值;
(2)若,且函数在上单调,求实数的值;
(3)令,若当时,总有,使得,求实数的取值范围.
29.如图,一座小岛距离海岸线上最近的点P的距离是3 km,从点P沿海岸正东12 km处有一个渔村.
(1)假设一个人驾驶的小船的平均速度为,步行的速度是.y(单位:h)表示他从小岛到渔村的时间,x(单位:km)表示此人将船停在海岸处A与P点的距离.请将y表示为x的函数,并写出定义域;
(2)在(1)的条件下,是否有一个停船的位置使得从小岛到渔村花费的时间最少 说明理由.()
30.一片森林原来面积为2014万亩,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐的面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的,已知到今年为止,森林剩余面积为原来的.
(1)求每年砍伐面积的百分比;
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
31.2013年9月22日,为应对台风“天兔”侵袭,我校食堂做好了充分准备,储备了至少三天的食物,食物在储藏时,有些易于保存,而有些却需要适当处理,如牛奶等,它们的保鲜时间会因储藏时温度的不同而不同,假定保鲜时间与储藏温度间的关系为指数型函数(且),若牛奶放在0℃的冰箱中,保鲜时间约为192时,放在22℃的厨房中,保鲜时间约为42时.
(1)写出保鲜时间(单位:时)关于储藏温度(单位:℃)的函数解析式;
(2)请运用(1)的结论计算,若我校购买的牛奶至少要储藏三天,则储藏时的温度最高约为多少?(精确到整数).(参考数据:)
32.某汽车租赁公司的月收益y(单位:元)与每辆车的月租金x(单位:元)间的关系为,那么,每辆车的月租金为多少元时,租赁公司的月收益最大?最大月收益是多少?
试卷第页,共页
试卷第页,共页
参考答案:
1.C
【解析】
【分析】
先利用补集运算求得B的补集,再利用交集运算求解.
【详解】
因为,
所以,
又,
所以,
故选:C.
2.A
【解析】
【分析】
取的中点,连结,则,则与平面所成角可转化为与平面所成角,过点作于点,则是与平面所成角,由此能求出与平面所成角的正弦值.
【详解】
取的中点,连结,则,
则与平面所成角可转化为与平面所成角,
过点作于点,
由于是正三棱柱,
平面平面,
平面,
是与平面所成角,
由题意,,
,
在中,,
与平面所成角的正弦值为.
故选:A
【点睛】
本题考查了线面角的求法,解题的关键是作出线面角,考查了考生的空间想象能力,属于基础题.
3.C
【解析】
【详解】
设AB边上的高为h,则S△ABC=|AB|·h.|AB|= ,AB边上的高h就是点C到直线AB的距离.AB边所在的直线方程为,即x+y-4=0.点C到直线x+y-4=0的距离为,因此,S△ABC=×2 ×=5.
4.B
【解析】
【分析】
利用函数的解析式知道当x<1时是以2周期的周期函数,故f(﹣2)=f(2),再代入函数解析式即得
【详解】
∵f(x)=,x=–2<1,∴f(–2)=f(0)=f(2),∵x=2>1,∴f(2)=log22=1,故选B.
5.C
【解析】
【分析】
分别计算出和时, S与t之间的函数关系,再结合四个选项即可判断出答案.
【详解】
当时,,
当时,,
分析四个选项可知,选C.
故选:C
【点睛】
本题考查了求分段函数的解析式,考查了函数的图象的识别,属于基础题.
6.C
【解析】
【分析】
因为容器中间凸,所以匀速注水时,开始和结束时水位高度变化快中间时水位高度变化慢,可知选C.
【详解】
结合容器的形状,可知一开始注水时,水高度变化较快当水位接近中部时变慢并持续一段时间,接近上部时,水位高度变快,故选C.
【点睛】
本题主要考查了对函数概念的理解及函数图象的认识,结合生活实践,属于中档题.
7.B
【解析】
【分析】
设,代入得到或,计算得到答案.
【详解】
设
则
或
综上:
故答案选B
【点睛】
本题考查了一次函数的计算,待定系数法是常规方法,需要灵活掌握和应用.
8.B
【解析】
根据题意,依次分析选项中函数的奇偶性与单调性,综合即可得答案.
【详解】
解:根据题意,依次分析选项:
对于A, ,为偶函数,不符合题意;
对于B,,为奇函数,当时,在上单调递增,符合题意;
对于C,为指数函数,不是奇函数,不符合题意;
对于D,为正弦函数,在区间上不是单调函数,不符合题意;
故选:B.
【点睛】
本题考查函数的奇偶性与单调性的判定,关键是掌握常见函数的奇偶性与单调性,属于基础题.
9.B
【解析】
【详解】
试题分析:由题意得,,又,所以,故选B.
考点:等比数列的性质.
10.D
【解析】
【分析】
利用导数的几何意义和导数的单调性判断.
【详解】
对于A,,则,若函数为增函数,则,随着的增大,减小,故满足条件;
对于B,,则,若函数为增函数,则,随着的增大,减小,故满足条件;
对于C,,则,若函数为增函数,则,随着的增大,减小,故满足条件;
对于D,,则,若函数为增函数,则,随着的增大,增大,不满足条件.
故选:D.
11.D
【解析】
【分析】
设的总产值为,我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的倍,然后根据平均增长率的定义列等式即可.
【详解】
本题为增长率模型函数,为指数函数形式.
设年总产值为,由于我国工农业总产值从年到年的年间翻了两番,说明年的工农业总产值是年工农业总产值的,则.
故选D.
【点睛】
本题考查平均增长律的定义,根据题意列式是解本题的关键,考查分析问题和解决问题的能力,属于基础题.
12.B
【解析】
【分析】
由题意列出关系式,并解不等式.
【详解】
设售价为,利润为,
则,
由题意,
即,
解得,
即售价应定为元到元之间,
故选:B.
13.B
【解析】
【分析】
根据保鲜时间与储藏温度满足函数关系:,并结合食品在的保鲜时间是144小时,在的保鲜时间是36小时,可求出,然后再将代入,即可得出答案.
【详解】
解:由题可知,保鲜时间与储藏温度满足函数关系:,
则,即,所以,
于是当时,=18(小时).
故选:B.
14.B
【解析】
根据函数在上单调递增,则对称轴求解.
【详解】
因为函数在上单调递增,
所以,
解得.
故选:B
【点睛】
本题主要考查二次函数的单调性的应用,属于基础题.
15.B
【解析】
【详解】
试题分析:依题意可知长方体底面面积为1.
设长方体底面一边长为,则底面另一边长为.
设水池总造价为元,
则
即,当且仅当即时取等号.
故B正确.
考点:1函数解析式;2基本不等式.
16.C
【解析】
【详解】
试题分析:由已知中某种产品平均每三年降低价格25%,目前售价为640元,我们易得9年后此产品共降价3次,代入计算即可得到答案:∵产品平均每三年降低价格25%,故9年后此产品共降价3次,又∵目前售价为640元,∴9年后此产品的价格为640×(1-25%)3=270元,故选C.
考点:本试题主要考查了是函数模型的选择与应用,指数的运算.
点评:其中根据已知判断出9年后此产品共降价3次,是解答本题的关键.
17. 2.5
【解析】
【分析】
利用分针逆时针转一周为60分钟,转过的角度为2π,得到10分钟是一周的六分之一,可得分针转的弧度.推导出1分钟时针逆时针转动0.5°,由此能求出将时钟慢5分钟,时针转动的角的大小.
【详解】
将时钟拨慢5分钟,分针、时针都是按逆时针方向转动,转过的角都是正角,这时,分针转过的角度是,即(弧度),时针转过的角度是.
故答案为,2.5.
【点睛】
本题考查弧度的定义,一周对的角是2π弧度.考查逆时针旋转得到的角是正角.注意任意角定义的合理运用.
18. 0 -3
【解析】
(1)先求f(3)的值,再求的值得解;(2)对a分类讨论解方程得解.
【详解】
(1)由题得f(3),所以.
(2)当a<0时,或,因为a<0,所以;
当a≥0时,,显然无实数解.
所以.
故答案为:(1)0;(2)-3.
【点睛】
本题主要考查分段函数的求值和应用,意在考查学生对这些知识的理解掌握水平.
19.6
【解析】
【分析】
根据分段函数的定义,分别求出和,计算即可求出结果.
【详解】
由题知,,
,
.
故答案为:6.
【点睛】
本题考查了分段函数求函数值的问题,考查了对数的运算.属于基础题.
20.
【解析】
【分析】
函数f(x)与g(x)图象上存在关于y轴对称的点,就是f(﹣x)=g(x)有解,也就是函数y=f(﹣x)与函数y=g(x)有交点,
在同一坐标系内画函数y=f(﹣x)(x>0)与函数y=g(x)=ln(x+a)的图象,结合图象解题.
【详解】
函数f(x)与g(x)图象上存在关于y轴有对称的点,
就是f(﹣x)=g(x)有解,
也就是函数y=f(﹣x)与函数y=g(x)有交点,
在同一坐标系内画函数y=f(﹣x)(x>0)与函数y=g(x)=ln(x+a)的图象:
∴函数y=g(x)=ln(x+a)的图象是把由函数y=lnx的图象向左平移
且平移到过点(0,)后开始,两函数的图象没有有交点,
把点(0,)代入y=ln(x+a)得,lna,∴a,
∴a,
故答案为:.
【点睛】
本题主要考查函数的图象,把方程的根的问题转化为函数图象的交点问题,体现了数形结合的思想.
21.19
【解析】
【分析】
根据题意得到距离地球约3500光年,一年走过的路程为,3500光年走过的路程为计算出结果即可.
【详解】
根据题意得到距离地球约3500光年,一年有秒,光速,
一年走过的路程为
3500光年走过的路程为
数量级为19.
故答案为:19.
22.6
【解析】
【分析】
利用对数运算求解.
【详解】
,
故答案为:6
23.
【解析】
根据题意,可得利润=售价-成本,将利润表示出来,得到关于的二次函数,再根据二次函数性质求解最大值即可.
【详解】
设利润为,则,当时,有最大值,
故答案为:18.
【点睛】
本题是函数的应用题,关键是建立函数的关系式求解,解函数应用题,一般可按照以下步骤进行:
(1)读题:读懂和深刻理解题意,找出等量关系,将应用问题转化为数学问题;
(2)建模:把主要关系近似化、形式化,抽象成数学问题;
(3)求解:化归为常规问题,选择合适的数学方法求解;
(4)评价:对结果进行验证或评估,对错误加以调节,最终将结果应用于现实.
24.(答案不唯一)
【解析】
【分析】
由f(x+y)=f(x)f(y),可得指数函数具有此性质,从而可得函数
【详解】
对于函数,
,
且当x>y时,f(x)>f(y),
所以函数满足条件,
故答案为:(答案不唯一)
25.(1);(2)见解析
【解析】
【分析】
(1)通过面积作差法求出函数的S=g(t)的解析式;
(2)根据函数单调性的定义证明函数的单调性即可.
【详解】
(1)由题意,可知
(2)由(1),知.
考虑函数,任取,且,则
因为,所以,,从而,,
因此.
故在上是增函数,注意到,所以在上是增函数.
【点睛】
本题考查了函数的单调性问题,考查求函数的解析式,是一道中档题
证明函数的单调性用定义法的步骤:①取值;②作差;③变形;④确定符号;⑤下结论
26.
【解析】
【分析】
由每年国内生产总值是上一年的倍得出函数关系式.
【详解】
因为每年的年平均增长率为b,所以年开始,每年国内生产总值是上一年的倍,所以x年后国内生产总值
27.(1);(2)
【解析】
【分析】
(1)利用正弦定理,结合和角的正弦公式,即可求角A的值:
(2)若AB=3,AC边上的中线BD的长为,求出AC,再求△ABC的面积.
【详解】
(1)由及正弦定理得:,
即,
即,
即,
因为,所以,则,又,所以.
(2)在中,,,,由余弦定理得
,所以,所以(负值舍去),
又为中点,所以.
【点睛】
本题考查正弦定理、余弦定理的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.
28.(1);(2);(3).
【解析】
【分析】
(1)根据偶函数图象关于轴对称,二次函数的一次项系数为0,可得的值;
(2)根据,可知时,取得最大值,且在,上是单调函数,即,即可求解实数的值.
(3)求解的值域和的值域,可得,即可求解实数的取值范围.
【详解】
(1)函数,为偶函数,
可得,
可得
即实数的值为;
(2)由,可知时,取得最大值,
即,
可得:
且在,上是单调函数,
,即
可得:.
当时,可得,
故得实数的值为.
(3)由,可得.
,,
,,
那么的值域,.
当,时,总有,,使得转化为函数的值域是的值域的子集;
即:当,时,
函数,
其对称轴,开口向下,
当时,即,可得(2);;
可得解:
当时,即可得;或;
此时无解.
当时,即,可得;(2);
此时无解.
综上可得实数的取值范围为,.
29.(1),;(2)当停船位置距离点约时,从小岛到渔村花费的时间最少;理由见解析
【解析】
【分析】
(1)利用路程除以速度可得时间,从而构造出函数关系式;
(2)利用定义法可证得函数在上单调递减,在上单调递增;由此可得当时,所花费时间最少.
【详解】
(1)由题意得:小岛距离点的距离为
一个人从小岛到处所需时间为,从处到渔村所需时间为
,
(2)当时,
,
函数在上单调递减
同理可得:函数在上单调递增
当时,()
当停船位置距离点约时,从小岛到渔村花费的时间最少
【点睛】
本题考查构造函数模型求解实际问题,涉及到最值问题的求解;求解最值问题的关键是能够判断出函数的单调区间,进而根据单调性得到最值点.
30.(1);(2)5;(3)15.
【解析】
【分析】
(1)设每年砍伐面积的百分比为,由指数函数的性质列式求解;
(2)由求解可得;
(3)由求解可得.
【详解】
(1)设每年砍伐面积的百分比为,则,解得;
(2)设到今年为止,该森林已砍伐了年,则,
,,;
(3)设今后最多还能砍伐年,
则,
,,.
答:(1)每年砍伐面积的百分比为;(2)到今年为止,该森林已砍伐了5年;(3)今后最多还能砍伐15年.
【点睛】
思路点睛:本题考查指数函数的应用,解题关键是根据每年砍伐的百分比相同,设百分比为,那么年后,剩余量为.抓住这个模型,通过解指数方程、指数不等式可得.
31.(1);(2)14℃.
【解析】
【分析】
(1)运用代入法进行求解即可;
(2)由(1)的函数解析式,根据题意得到不等式,利用换底公式进行求解即可.
【详解】
(1)设(且),则有,,.
(2)依题意有,
若我校购买的牛奶至少要储藏三天,则储藏时的温度最高约为14℃.
32.4050元,最大月收益307050元
【解析】
将函数化为顶点式,由二次函数的性质即可得出结论.
【详解】
解:,∴当时,.即每辆车的月租金为4050元时,租赁公司的月收益最大,最大月收益是307050元.
【点睛】
本题主要考查了二次函数模型解决实际问题,属于中等题.
试卷第页,共页
试卷第页,共页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
