人教A版(2019)必修第一册逆袭之路第五章5.7三角函数的应用(word版含解析)
文档属性
| 名称 | 人教A版(2019)必修第一册逆袭之路第五章5.7三角函数的应用(word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-25 15:30:04 | ||
图片预览


文档简介
人教A版(2019)必修第一册逆袭之路第五章5.7三角函数的应用
一、单选题
1.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|)的部分图象如图所示,则f(x)的解析式为( )
A.f(x)=sin(x)﹣1 B.f(x)=2sin(x)﹣1
C.f(x)=2sin(x)﹣1 D.f(x)=2sin(2x)+1
2.已知函数f(x)=sin(2x+),其中为实数,若f(x)≤|f()|对x∈R恒成立,且f()>0,则f(x)的单调递减区间是
A.[kπ,kπ+](k∈Z) B.[kπ–,kπ+](k∈Z)
C.[kπ+,kπ+](k∈Z) D.[kπ–,kπ](k∈Z)
3.已知函数f(x)sincos(ω>0),如果存在实数x0,使得对任意的实数x,都有f(x0﹣2020)≤f(x)≤f(x0)成立,则ω的最大值为( )
A.2020 B.4040 C.1010 D.
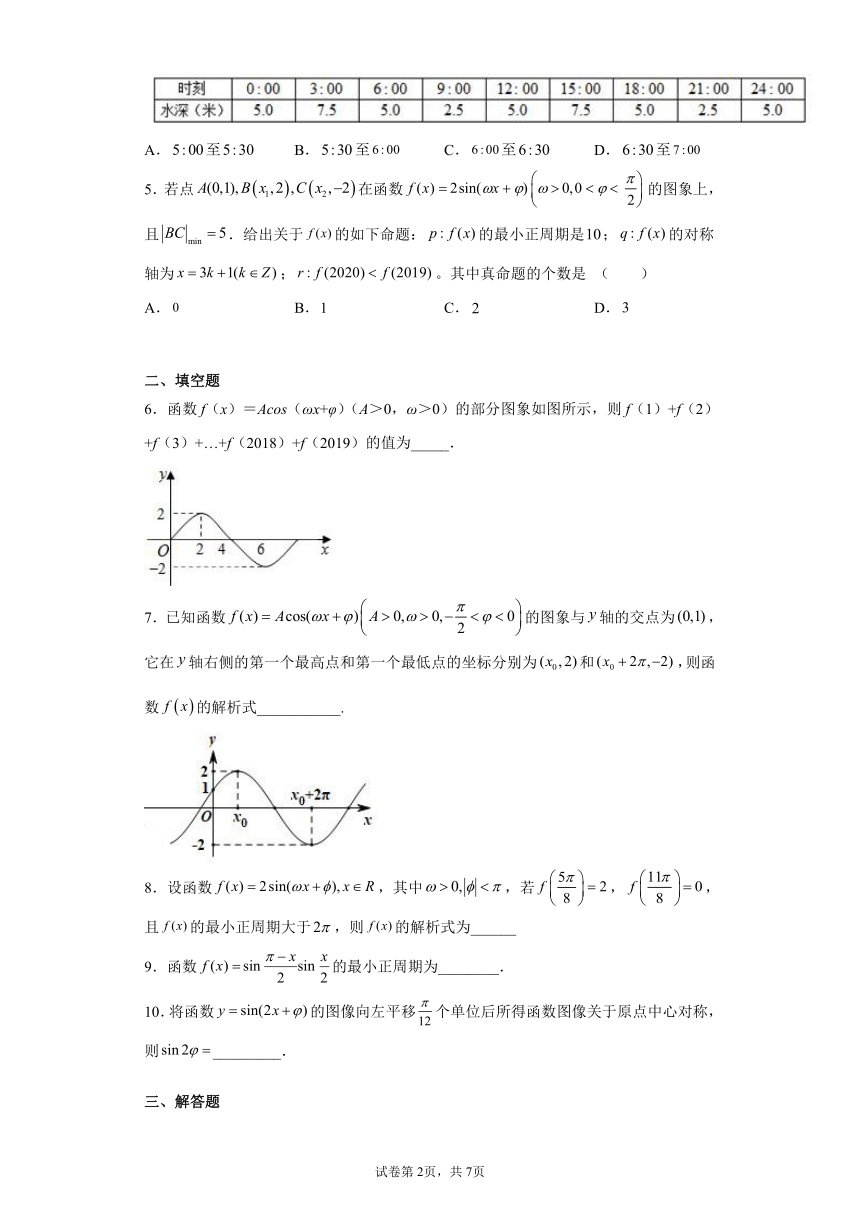
4.海水受日月的引力,在一定的时候发生潮涨潮落,船只一般涨潮时进港卸货,落潮时出港航行,某船吃水深度(船底与水面距离)为米,安全间隙(船底与海底距离)为米,该船在开始卸货,吃水深度以米/小时的速度减少,该港口某季节每天几个时刻的水深如下表所示,若选择()拟合该港口水深与时间的函数关系,则该船必须停止卸货驶离港口的时间大概控制在(要考虑船只驶出港口需要一定时间)
A.至 B.至 C.至 D.至
5.若点在函数的图象上,且.给出关于的如下命题:的最小正周期是;的对称轴为;。其中真命题的个数是 ( )
A. B. C. D.
二、填空题
6.函数f(x)=Acos(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2018)+f(2019)的值为_____.
7.已知函数的图象与轴的交点为,它在轴右侧的第一个最高点和第一个最低点的坐标分别为和,则函数的解析式___________.
8.设函数,其中,若,,且的最小正周期大于,则的解析式为______
9.函数的最小正周期为________.
10.将函数的图像向左平移个单位后所得函数图像关于原点中心对称,则_________.
三、解答题
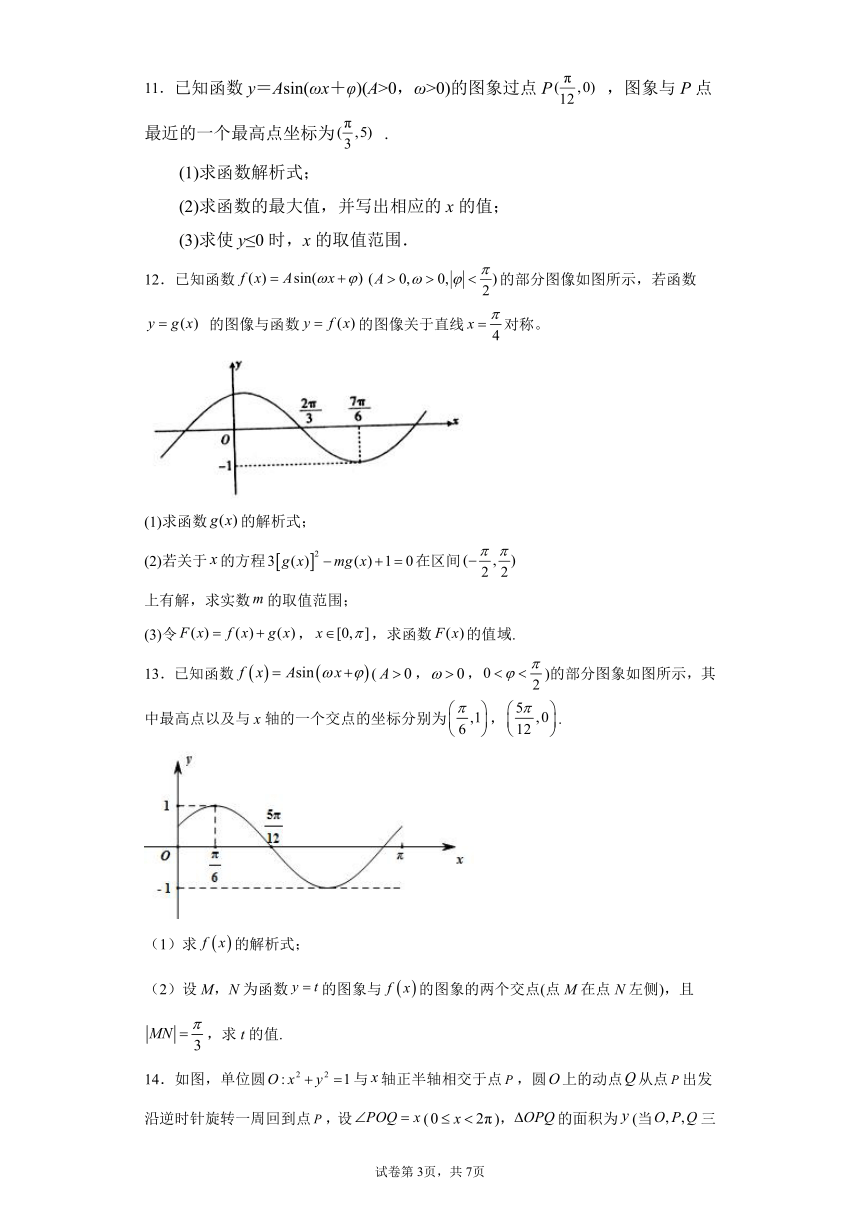
11.已知函数y=Asin(ωx+φ)(A>0,ω>0)的图象过点P ,图象与P点最近的一个最高点坐标为 .
(1)求函数解析式;
(2)求函数的最大值,并写出相应的x的值;
(3)求使y≤0时,x的取值范围.
12.已知函数的部分图像如图所示,若函数 的图像与函数的图像关于直线对称。
(1)求函数的解析式;
(2)若关于的方程在区间
上有解,求实数的取值范围;
(3)令,,求函数的值域.
13.已知函数(,,)的部分图象如图所示,其中最高点以及与x轴的一个交点的坐标分别为,.
(1)求的解析式;
(2)设M,N为函数的图象与的图象的两个交点(点M在点N左侧),且,求t的值.
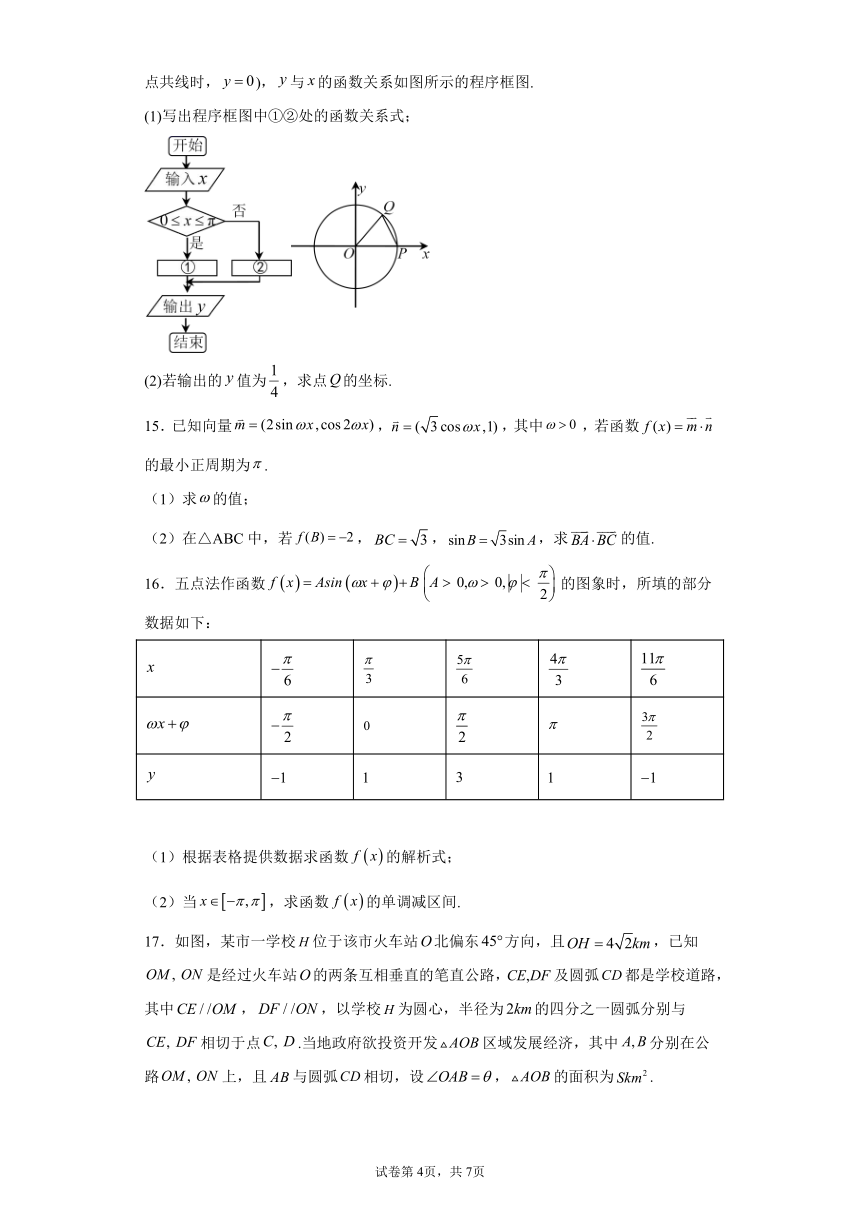
14.如图,单位圆与轴正半轴相交于点,圆上的动点从点出发沿逆时针旋转一周回到点,设(),的面积为(当三点共线时,),与的函数关系如图所示的程序框图.
(1)写出程序框图中①②处的函数关系式;
(2)若输出的值为,求点的坐标.
15.已知向量,,其中,若函数的最小正周期为.
(1)求的值;
(2)在△ABC中,若,,,求的值.
16.五点法作函数的图象时,所填的部分数据如下:
(1)根据表格提供数据求函数的解析式;
(2)当,求函数的单调减区间.
17.如图,某市一学校位于该市火车站北偏东方向,且,已知是经过火车站的两条互相垂直的笔直公路,CE,DF及圆弧都是学校道路,其中,,以学校为圆心,半径为的四分之一圆弧分别与相切于点.当地政府欲投资开发区域发展经济,其中分别在公路上,且与圆弧相切,设,的面积为.
(1)求关于的函数解析式;
(2)当为何值时,面积为最小,政府投资最低?
18.已知函数.任取,若函数在区间上的最大值为,最小值为,记.
(1)求函数的最小正周期及对称轴方程;
(2)当时,求函数的解析式;
(3)设函数,,其中实数为参数,且满足关于的不等式有解.若对任意,存在,使得成立,求实数的取值范围.
19.已知函数.
(1)若,求;
(2)求的周期,单调递增区间.
20.在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南方向300km的海面P处,并以20km/h的速度向西偏北方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
21.借助计算器或计算机,用二分法求方程的近似解(精确到).
22.已知函数的图象如图所示.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度,得到函数设,求函数上的最大值.
23.如图为一个观览车示意图.该观览车圆半径为米,圆上最低点与地面距离为米,秒转动一圈,图中与地面垂直.设从开始转动,逆时针转动角到,设点与地面距离为.
(1)当时,求的值;
(2)若经过秒到达,求与的函数解析式.
24.已知椭圆,A是椭圆的右顶点,B是椭圆的上顶点,直线与椭圆交于M、N两点,且M点位于第一象限.
(1)若,证明:直线和的斜率之积为定值;
(2)若,求四边形的面积的最大值.
25.函数的部分图象如图所示.
(1)求函数的解析式;
(2)求函数的单调增区间.
26.张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元及以上,顾客就少付元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
(1)若顾客一次购买松子和腰果各1千克,需要支付180元,试求x的值.
(2)在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,试求x的最大值.
27.如图是函数的一段图像.
(1)求此函数解析式;
(2)分析一下该函数图像可以由函数的图像经过怎样的变换得到.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【分析】
由已知列式求得的值,再由周期求得的值,利用五点作图的第二个点求得的值,即可得到答案.
【详解】
由题意,根据三角函数的图象,可得,解得,
又由,解得,则,
又由五点作图的第二个点可得:,解得,
所以函数的解析式为,故选D.
【点睛】
本题主要考查了由的部分图象求解函数的解析式,其中解答中熟记三角函数的五点作图法,以及三角函数的图象与性质是解答的关键,着重考查了推理与运算能力,属于中档试题.
2.C
【分析】
由题意可得2φ=kπ,k∈z,即 φ=kπ,k∈z①,再由f()=sin(φ)>0 ②,求得φ=0,可得f(x)=sin2x.令2kπ2x≤2kπ,k∈z,求得x的范围,可得函数的减区间.
【详解】
由题意可得函数f(x)=sin(2x+φ)的图象关于直线x=对称,故有2×+φ=kπ+,k∈Z,即φ=kπ,k∈Z①.又f()=sin(+φ)>0②,由①②可得φ=2kπ,k∈Z,
∴f(x)=sin2x.令2kπ+≤2x≤2kπ+,k∈Z,解得kπ+≤x≤kπ+,k∈Z,
故函数的减区间为[kπ+,kπ+],k∈Z,
故选:C.
【点睛】
本题主要考查正弦函数的图象性质,考查对称性及单调性,准确计算是关键,属于中档题.
3.A
【分析】
利用辅助角公式对函数化简可得f(x)sincos2sin(),由对任意的实数x,都有f(x0﹣2020)≤ f(x)≤ f(x0)成立可得,两端点值分别为函数的最小值和最大值,要使得ω 最大,只要周期最大,当2020,周期最大,代入即可求得解.
【详解】
利用辅助角公式对函数化解可得f (x)sincos2sin(),
由对任意的实数x,对任意的实数x,都有f(x0﹣2020)≤ f(x)≤ f(x0)成立;
可得f(x0),f(x0-2020),分别为函数的最大值和最小值,
要使得ω最大,只要周期最大,
当2020即T=4040=2ω时,周期最大,此时ω=2020.
故选:A.
【点睛】
本题考查了三角函数辅助角公式的应用及三角函数的性质的应用,解题的关键是根据条件求得函数的最小值和最大值,属于中档题.
4.C
【解析】
由题意得,函数的周期为,振幅,所以,
又因为达到最大值,
所以由,可得,
所以,所以函数的表达式为,
令,解得,所以在可安全离港,故选C.
5.C
【分析】
因为在函数的图象上,可求得,根据,,可求得,即可求得,逐项判断命题,即可求得答案.
【详解】
在函数的图象上
即 ,
又
,
,
对于命题,
命题为假命题;
对于命题,对称轴为,
命题为真命题;
对于命题,,
命题为真命题.
故正确命题个数为:
故选:C.
【点睛】
本题解题关键是掌握正弦函数的图象特征和三角函数的基础知识,考查了分析能力和计算能力,属于中档题.
6.2+2
【分析】
先由图像求得余弦型函数的解析式,然后再由函数的周期性化简,进而求解.
【详解】
由图象可得:A=2,周期T=4(4-2)=8,∴ω,由图象过点(2,2),
即,得,则
由T=8,则
,
∵,
则
2sin2sin2sin2+2.
故答案为:.
【点睛】
本题考查了数形结合求余弦型函数解析式,考查了余弦型函数周期性的应用,属于一般难度的题.
7.
【分析】
由三角函数图像与性质求出,,,,即得的解析式.
【详解】
由图像可知且,故,由知,
又由轴右侧的第一个最高点和第一个最低点的坐标可知,,
故,故.
故答案为:.
【点睛】
本题考查了三角函数的图像与解析式,属于基础题.
8.
【分析】
根据最小正周期大于,可得T的取值范围,结合两个定点的特征,即可求得周期.将一个最大值的坐标代入,即可求得的值,进而得函数的解析式.
【详解】
因为的最小正周期大于
所以,即
因为,
所以
则
由周期公式可得
所以
因为,代入可得
即
因为
所以当时,解得
综上可知,函数的解析式为
故答案为:
【点睛】
本题考查了三角函数的周期性及函数解析式的求法,求的值时选择代入最高或者最低点,属于基础题.
9.2
【解析】
故函数的最小正周期
即答案为
10.
【分析】
先根据函数平移变换得平移后的解析式为,再根据其图象关于原点中心对称得,进而计算得.
【详解】
解:根据题意得函数的图像向左平移个单位后得到的函数解析式为:,
由函数图象关于原点中心对称,
故,即
所以.
故答案为:
【点睛】
三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母而言.
函数是奇函数 ;
函数是偶函数;
函数是奇函数;
函数是偶函数.
11.(1) (2) (3)
【解析】
试题分析:(1)由最高点可得A=5,由图象与P点最近的距离可得四分之一个周期,解得ω,最后根据最大值求φ(2)由正弦函数性质确定最大值取法: ,解方程可得x的值;(3)利用正弦函数性质解三角不等式可得2kπ-π≤2x- ≤2kπ,即得x的取值范围.
试题解析:解:(1)由题意知=-=,∴T=π.
∴ω==2,由ω·+φ=0,得φ=-,又A=5,
∴y=5sin.
(2)函数的最大值为5,此时2x-=2kπ+ (k∈Z).∴x=kπ+ (k∈Z)
(3)∵5sin≤0,
∴2kπ-π≤2x-≤2kπ(k∈Z).
∴kπ-≤x≤kπ+ (k∈Z).
点睛:已知函数的图象求解析式
(1).
(2)由函数的周期求
(3)利用“五点法”中相对应的特殊点求
12.(1);(2);(3).
【解析】
试题分析:
(1)利用题意分别求得 可得函数的解析式为;
(2)利用题意结合二次型复合函数的性质可得实数的取值范围是;
(3)整理函数的解析式,结合角的范围可得函数的值域为.
试题解析:
(1)由图可知,,
,,,,
由于,故即.
。
(2),,即.
又,,
①当时,;
②当时,;
③当时,;
综上,实数的取值范围是
(3) ,
。
又,,,
即,
函数函数的值域为。
点睛:已知f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象求其解析式时,A比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:
(1)由即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0,则令ωx0+φ=0(或ωx0+φ=π),即可求出φ.
(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.
13.(1);(2).
【分析】
(1)由周期求出,取点求出,进而得出的解析式;
(2)设,,解方程,得出,再由求出t的值.
【详解】
解:(1)由题意易知,周期,所以,所以.
将最高点代入中可得
得,即.
又因为,所以,所以.
(2)设,,则
所以
所以,所以,即
所以.
【点睛】
方法点睛:由图象求函数的解析式时,有如下步骤:
1、由最值得出的值;
2、由周期结合得出;
3、取点求出.
14.(1)见解析;(2)见解析
【解析】
【分析】
(1)通过实际问题得到与的函数关系为分段函数,从而判断出程序框填的结果.
(2)分类讨论时和时两种情形下的点Q坐标,从而得到答案.
【详解】
(1)当时,,
当时,
函数的解析式为,
故程序框图中①②处的函数关系式分别是,
(2)时,令,即,或,点的坐标为或
时,令,即,或,点的坐标为或
故点的坐标为
【点睛】
本题主要考查算法框图,三角函数的运用,意在考查学生的数形结合思想,分析实际问题的能力.
15.(1)1;(2)
【分析】
(1),利用三角函数的周期性可求ω的值.
(2)根据f(B)的值,求得B,由正弦定理求得A,最后求得C,利用向量的数量积公式求得答案.
【详解】
(1)
∵的最小正周期为,∴,∴.
(2)设△ABC中角A,B,C所对的边分别是a,b,c.
∵,∴,即,解得.
∵,∴,∵,∴,∴,,
∵,∴,,∴,∴.
【点睛】
本题主要考查了三角函数图象与性质,向量的数量积运算,三角函数恒等变换的应用.综合考查了学生分析问题和运算能力.
16.(1);(2).
【解析】
分析:(1)由表中的最大值和最小值可得的值,通过,可求,根据对称中心点坐标可知,图象过代入求解,可得函数的解析式;(2)结合函数图象:当时,函数的减区间是.
详解:由表中的最大值为3,最小值为﹣1,可得A=,
由=T,则T=2π.∴,
∵y=2sin(ωx+φ)的最大值是2,故得B=3﹣2=1.
此时函数f(x)=2sin(x+φ)+1.
∵图象过(﹣)带入可得:﹣1=2sin(+φ)+1,
可得:φ=﹣,(k∈Z).
解得:φ=,∵φ,∴φ=﹣.
故得函数f(x)的解析式为f(x)=2sin(x﹣)+1 .
(2)结合函数图象:当时,函数的减区间是.
点睛: 已知三角函数的性质求解析式的步骤:利用最值求出 ,利用最值点或零点的间隔先求出周期,用周期公式求出,利用特殊点求出,正确求是解题的关键.求解析时求参数是确定函数解析式的关键,由特殊点求时,一定要分清特殊点是“五点法”的第几个点.
17.(1);(2).
【分析】
(1)以点为坐标原点建立如图所示的平面直角坐标系,则,在中,设,又,故,,进而表示直线的方程,由直线与圆相切构建关系化简整理得,即可表示OA,OB,最后由三角形面积公式表示面积即可;
(2)令,则,由辅助角公式和三角函数值域可求得t的取值范围,进而对原面积的函数用含t的表达式换元,再令进行换元,并构建新的函数,由二次函数性质即可求得最小值.
【详解】
解:(1)以点为坐标原点建立如图所示的平面直角坐标系,则,在中,设,又,故,.
所以直线的方程为,即.
因为直线与圆相切,
所以.
因为点在直线的上方,
所以,
所以式可化为,解得.
所以,.
所以面积为.
(2)令,则,
且,
所以,.
令,,所以在上单调递减.
所以,当,即时,取得最大值,取最小值.
答:当时,面积为最小,政府投资最低.
【点睛】
本题考查三角函数的实际应用,应优先结合实际建立合适的数学模型,再按模型求最值,属于难题.
18.(1)最小正周期为,对称轴方程为;(2);(3).
【分析】
(1)由正弦型函数的周期公式可求得函数的最小正周期,解方程,可得出函数的对称轴方程;
(2)对实数的取值进行分类讨论,分析函数在区间上的单调性,求得、,即可求得的表达式;
(3)利用已知条件求得,分析可知函数在的值域是函数在的值域的子集,分、两种情况讨论,将问题转化为,综合可得出实数的取值范围.
【详解】
(1)函数的最小正周期为,
解方程,可得,
故函数的对称轴方程为;
(2)分以下几种情况讨论:
①当时,,,
当时,,
此时函数在区间上单调递减,在上单调递增,
所以,,,
则;
②当时,,,
当时,,
此时函数在区间上单调递减,在上单调递增,
所以,,,
则;
③当时,,,
当时,,
此时函数在上单调递增,则,,
则.
综上所述,;
(3)因为函数的最小正周期为,所以,,,
则,
所以,函数是以为周期的周期函数,研究函数的性质,只需研究函数在时的性质即可.
仿照(2)可得,
当时,;
当时,;
当时,.
所以,当时,,同理可知当时,.
作出函数的图象如下图所示:
所以,函数的值域为,
因为,则,所以,,
对任意的,存在,使得成立,
即函数在的值域是函数在的值域的子集,
因为.
当时,因为函数在上单调递减,在上单调递增,
所以,,
因为函数在上单调递增,
所以,,所以,,解得;
当时,因为函数在上单调递减,所以,,
,
所以,函数在上单调递减,在上单调递增,
所以,,所以,,即,
因为,则,令,则,
作出函数与函数的图象如下图所示:
有图可知,当时,;当时,.
此时,,解得.
综上所述,实数的取值范围是.
【点睛】
结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数,,,.
(1)若,,有成立,则;
(2)若,,有成立,则;
(3)若,,有成立,则;
(4)若,,有成立,则的值域是的值域的子集.
19.(1);(2)见解析
【分析】
(1)分子分母同除1,利用,把分母变形,然后分子分母同除 ,利用齐次式求,(2)利用辅助角公式把f(x)化为的形式,再利用正余弦函数的单调性求单调区间.
【详解】
(1)
,
(2)
周期为
由
可得
所以递增区间.
【点睛】
本题考查三角函数齐次式的应用,三角函数辅助角公式以及求单调区间,解题关键是转化为齐次式,属于基础题.
20.12小时后该城市开始受到台风的侵袭
【详解】
设在t时刻台风中心位于点Q,此时|OP|=300,|PQ|=20t,
台风侵袭范围的圆形区域半径为10t+60,
由,可知,
cos∠OPQ=cos(θ-45o)= cosθcos45o+sinθsin45o=
在 △OPQ中,由余弦定理,得
=
=
若城市O受到台风的侵袭,则有|OQ|≤r(t),即
,
整理,得,解得12≤t≤24,
答:12小时后该城市开始受到台风的侵袭.
21.0.5.
【分析】
先构造函数,求函数的定义域,根据函数的单调性可以确定函数零点的个数,取特殊值确定作为计算的初始区间,然后列表运用二分法求方程的近似解的方法,结合要求精确到,求出方程的近似解.
【详解】
令,函数的定义域为.
因为函数在上是增函数,所以至多有一个零点.
又因为,,所以方程在内有唯一一个实数解.
用二分法逐次计算,列表如下:
区间 中点的值 中点函数值(或近似值)
由于区间内的所有值,若精确到0.1,都是0.5,所以0.5是方程精确到0.1的近似解.
【点睛】
本题考查了二分法的应用. 本题中利用函数的单调性确定了初始区间,也可以在平面直角坐标系中画出函数与函数的图象,根据图象确定初始区间..
22.(1);(2).
【分析】
(1)根据图像可得振幅,最小正周期,则.
由,又,则易求得,即可得解.
(2)利用辅助角公式可得:
,再根据定义域即可得解.
【详解】
(1)由图象可得,
最小正周期,则.
由,
又,则易求得,
所以;
(2)由题意知,
所以
,
因为,所以,
所以.
【点睛】
本题考查了利用三角函数图像求解析式,考查了辅助角公式,在解题过程中注意各个量的对应关系,以及相关量的取值范围,整体难度不大,属于中档题.
23.
(1);
(2).
【分析】
(1)以圆心为原点,建立平面直角坐标系,利用三角函数的定义写出点的坐标,再代入进行求值;
(2)根据点在圆上运动的周期求出角速度,再写出与的函数解析式即可.
(1)
解:以圆心为原点,建立平面直角坐标系(如图所示),
则以为始边、为终边的角为,
故点的坐标为,
所以,
当时,
(米).
(2)
解:点在圆上转动的周期为60秒,
所以角速度为,
故秒转过的弧度数为,
所以与的函数解析式为:
().
24.(1)证明见解析;(2).
【分析】
(1)设,则,利用两点的斜率公式以及点在椭圆上可得定值;
(2)联立直线与椭圆方程,求出到的距离和到的距离,利用根与系数的关系可得面积的最大值.
【详解】
(1)证明:设,则,
∵,,∴,,
∵在椭圆上,∴
∴为定值.
(2)设,依题意:,点在第一象限,∴.
联立:得:,
∴,,
设到的距离为,到的距离为,
∴,,
∴.
又∵
(当时取等号),
∴.
∴四边形的面积的最大值为
25.(1);(2)
【分析】
(1)根据三角函数的图像可得以及周期,根据周期公式求出,再由求出即可求解.
(2)根据正弦函数的单调递增区间,整体代入解不等式即可.
【详解】
(1)由三角函数的图像可得,,
由,解得,
又,即,
所以,所以,
解得,
因为,所以,
所以.
(2)由(1),
则,
解得,
所以函数的单调增区间为.
【点睛】
本题考查了由三角函数的图像求解析式、求三角函数的单调区间,考查了基本运算求解能力,属于基础题.
26.(1)10;(2)18.
【分析】
(1)根据题意求出总价后可得优惠价;
(2)设是总价,据题意,在时,列出不等式,解之可得,注意分类讨论.
【详解】
(1)顾客一次购买松子和腰果各1千克,总价为元,支付元(元);
(2)设订单总价为,若,没有优惠,符合题意,
若,则,,而,所以,又,所以,最大值为.
27.(1);(2)变换情况见解析.
【分析】
(1)由求,由求,再代入点求,即可求得解析式;
(2)利用三角函数的图像变换可得解.
【详解】
(1)由图像知,解得,
由,,.
当时,,,又,,
所以所求函数解析式为.
(2)把函数图像上的所有点,向左平移个单位,得到图像,
然后把函数图像上的所有点,纵坐标保持不变,横坐标缩短为原来的,得到的图像,
再把函数图像上的所有点,横坐标保持不变,纵坐标变为原来的,得到的图像,
最后把函数图像上的所有点,向下平移1个单位,得到的图像.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知函数f(x)=Asin(ωx+φ)+B(A>0,ω>0,|φ|)的部分图象如图所示,则f(x)的解析式为( )
A.f(x)=sin(x)﹣1 B.f(x)=2sin(x)﹣1
C.f(x)=2sin(x)﹣1 D.f(x)=2sin(2x)+1
2.已知函数f(x)=sin(2x+),其中为实数,若f(x)≤|f()|对x∈R恒成立,且f()>0,则f(x)的单调递减区间是
A.[kπ,kπ+](k∈Z) B.[kπ–,kπ+](k∈Z)
C.[kπ+,kπ+](k∈Z) D.[kπ–,kπ](k∈Z)
3.已知函数f(x)sincos(ω>0),如果存在实数x0,使得对任意的实数x,都有f(x0﹣2020)≤f(x)≤f(x0)成立,则ω的最大值为( )
A.2020 B.4040 C.1010 D.
4.海水受日月的引力,在一定的时候发生潮涨潮落,船只一般涨潮时进港卸货,落潮时出港航行,某船吃水深度(船底与水面距离)为米,安全间隙(船底与海底距离)为米,该船在开始卸货,吃水深度以米/小时的速度减少,该港口某季节每天几个时刻的水深如下表所示,若选择()拟合该港口水深与时间的函数关系,则该船必须停止卸货驶离港口的时间大概控制在(要考虑船只驶出港口需要一定时间)
A.至 B.至 C.至 D.至
5.若点在函数的图象上,且.给出关于的如下命题:的最小正周期是;的对称轴为;。其中真命题的个数是 ( )
A. B. C. D.
二、填空题
6.函数f(x)=Acos(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(2018)+f(2019)的值为_____.
7.已知函数的图象与轴的交点为,它在轴右侧的第一个最高点和第一个最低点的坐标分别为和,则函数的解析式___________.
8.设函数,其中,若,,且的最小正周期大于,则的解析式为______
9.函数的最小正周期为________.
10.将函数的图像向左平移个单位后所得函数图像关于原点中心对称,则_________.
三、解答题
11.已知函数y=Asin(ωx+φ)(A>0,ω>0)的图象过点P ,图象与P点最近的一个最高点坐标为 .
(1)求函数解析式;
(2)求函数的最大值,并写出相应的x的值;
(3)求使y≤0时,x的取值范围.
12.已知函数的部分图像如图所示,若函数 的图像与函数的图像关于直线对称。
(1)求函数的解析式;
(2)若关于的方程在区间
上有解,求实数的取值范围;
(3)令,,求函数的值域.
13.已知函数(,,)的部分图象如图所示,其中最高点以及与x轴的一个交点的坐标分别为,.
(1)求的解析式;
(2)设M,N为函数的图象与的图象的两个交点(点M在点N左侧),且,求t的值.
14.如图,单位圆与轴正半轴相交于点,圆上的动点从点出发沿逆时针旋转一周回到点,设(),的面积为(当三点共线时,),与的函数关系如图所示的程序框图.
(1)写出程序框图中①②处的函数关系式;
(2)若输出的值为,求点的坐标.
15.已知向量,,其中,若函数的最小正周期为.
(1)求的值;
(2)在△ABC中,若,,,求的值.
16.五点法作函数的图象时,所填的部分数据如下:
(1)根据表格提供数据求函数的解析式;
(2)当,求函数的单调减区间.
17.如图,某市一学校位于该市火车站北偏东方向,且,已知是经过火车站的两条互相垂直的笔直公路,CE,DF及圆弧都是学校道路,其中,,以学校为圆心,半径为的四分之一圆弧分别与相切于点.当地政府欲投资开发区域发展经济,其中分别在公路上,且与圆弧相切,设,的面积为.
(1)求关于的函数解析式;
(2)当为何值时,面积为最小,政府投资最低?
18.已知函数.任取,若函数在区间上的最大值为,最小值为,记.
(1)求函数的最小正周期及对称轴方程;
(2)当时,求函数的解析式;
(3)设函数,,其中实数为参数,且满足关于的不等式有解.若对任意,存在,使得成立,求实数的取值范围.
19.已知函数.
(1)若,求;
(2)求的周期,单调递增区间.
20.在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南方向300km的海面P处,并以20km/h的速度向西偏北方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
21.借助计算器或计算机,用二分法求方程的近似解(精确到).
22.已知函数的图象如图所示.
(1)求的解析式;
(2)将函数的图象向右平移个单位长度,得到函数设,求函数上的最大值.
23.如图为一个观览车示意图.该观览车圆半径为米,圆上最低点与地面距离为米,秒转动一圈,图中与地面垂直.设从开始转动,逆时针转动角到,设点与地面距离为.
(1)当时,求的值;
(2)若经过秒到达,求与的函数解析式.
24.已知椭圆,A是椭圆的右顶点,B是椭圆的上顶点,直线与椭圆交于M、N两点,且M点位于第一象限.
(1)若,证明:直线和的斜率之积为定值;
(2)若,求四边形的面积的最大值.
25.函数的部分图象如图所示.
(1)求函数的解析式;
(2)求函数的单调增区间.
26.张军自主创业,在网上经营一家干果店,销售的干果中有松子、开心果、腰果、核桃价格依次为120元/千克、80元/千克、70元/千克、40元千克,为增加销量,张军对这四种干果进行促销:一次购买干果的总价达到150元及以上,顾客就少付元.每笔订单顾客网上支付成功后,张军会得到支付款的80%.
(1)若顾客一次购买松子和腰果各1千克,需要支付180元,试求x的值.
(2)在促销活动中,为保证张军每笔订单得到的金额均不低于促销前总价的七折,试求x的最大值.
27.如图是函数的一段图像.
(1)求此函数解析式;
(2)分析一下该函数图像可以由函数的图像经过怎样的变换得到.
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.D
【分析】
由已知列式求得的值,再由周期求得的值,利用五点作图的第二个点求得的值,即可得到答案.
【详解】
由题意,根据三角函数的图象,可得,解得,
又由,解得,则,
又由五点作图的第二个点可得:,解得,
所以函数的解析式为,故选D.
【点睛】
本题主要考查了由的部分图象求解函数的解析式,其中解答中熟记三角函数的五点作图法,以及三角函数的图象与性质是解答的关键,着重考查了推理与运算能力,属于中档试题.
2.C
【分析】
由题意可得2φ=kπ,k∈z,即 φ=kπ,k∈z①,再由f()=sin(φ)>0 ②,求得φ=0,可得f(x)=sin2x.令2kπ2x≤2kπ,k∈z,求得x的范围,可得函数的减区间.
【详解】
由题意可得函数f(x)=sin(2x+φ)的图象关于直线x=对称,故有2×+φ=kπ+,k∈Z,即φ=kπ,k∈Z①.又f()=sin(+φ)>0②,由①②可得φ=2kπ,k∈Z,
∴f(x)=sin2x.令2kπ+≤2x≤2kπ+,k∈Z,解得kπ+≤x≤kπ+,k∈Z,
故函数的减区间为[kπ+,kπ+],k∈Z,
故选:C.
【点睛】
本题主要考查正弦函数的图象性质,考查对称性及单调性,准确计算是关键,属于中档题.
3.A
【分析】
利用辅助角公式对函数化简可得f(x)sincos2sin(),由对任意的实数x,都有f(x0﹣2020)≤ f(x)≤ f(x0)成立可得,两端点值分别为函数的最小值和最大值,要使得ω 最大,只要周期最大,当2020,周期最大,代入即可求得解.
【详解】
利用辅助角公式对函数化解可得f (x)sincos2sin(),
由对任意的实数x,对任意的实数x,都有f(x0﹣2020)≤ f(x)≤ f(x0)成立;
可得f(x0),f(x0-2020),分别为函数的最大值和最小值,
要使得ω最大,只要周期最大,
当2020即T=4040=2ω时,周期最大,此时ω=2020.
故选:A.
【点睛】
本题考查了三角函数辅助角公式的应用及三角函数的性质的应用,解题的关键是根据条件求得函数的最小值和最大值,属于中档题.
4.C
【解析】
由题意得,函数的周期为,振幅,所以,
又因为达到最大值,
所以由,可得,
所以,所以函数的表达式为,
令,解得,所以在可安全离港,故选C.
5.C
【分析】
因为在函数的图象上,可求得,根据,,可求得,即可求得,逐项判断命题,即可求得答案.
【详解】
在函数的图象上
即 ,
又
,
,
对于命题,
命题为假命题;
对于命题,对称轴为,
命题为真命题;
对于命题,,
命题为真命题.
故正确命题个数为:
故选:C.
【点睛】
本题解题关键是掌握正弦函数的图象特征和三角函数的基础知识,考查了分析能力和计算能力,属于中档题.
6.2+2
【分析】
先由图像求得余弦型函数的解析式,然后再由函数的周期性化简,进而求解.
【详解】
由图象可得:A=2,周期T=4(4-2)=8,∴ω,由图象过点(2,2),
即,得,则
由T=8,则
,
∵,
则
2sin2sin2sin2+2.
故答案为:.
【点睛】
本题考查了数形结合求余弦型函数解析式,考查了余弦型函数周期性的应用,属于一般难度的题.
7.
【分析】
由三角函数图像与性质求出,,,,即得的解析式.
【详解】
由图像可知且,故,由知,
又由轴右侧的第一个最高点和第一个最低点的坐标可知,,
故,故.
故答案为:.
【点睛】
本题考查了三角函数的图像与解析式,属于基础题.
8.
【分析】
根据最小正周期大于,可得T的取值范围,结合两个定点的特征,即可求得周期.将一个最大值的坐标代入,即可求得的值,进而得函数的解析式.
【详解】
因为的最小正周期大于
所以,即
因为,
所以
则
由周期公式可得
所以
因为,代入可得
即
因为
所以当时,解得
综上可知,函数的解析式为
故答案为:
【点睛】
本题考查了三角函数的周期性及函数解析式的求法,求的值时选择代入最高或者最低点,属于基础题.
9.2
【解析】
故函数的最小正周期
即答案为
10.
【分析】
先根据函数平移变换得平移后的解析式为,再根据其图象关于原点中心对称得,进而计算得.
【详解】
解:根据题意得函数的图像向左平移个单位后得到的函数解析式为:,
由函数图象关于原点中心对称,
故,即
所以.
故答案为:
【点睛】
三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母而言.
函数是奇函数 ;
函数是偶函数;
函数是奇函数;
函数是偶函数.
11.(1) (2) (3)
【解析】
试题分析:(1)由最高点可得A=5,由图象与P点最近的距离可得四分之一个周期,解得ω,最后根据最大值求φ(2)由正弦函数性质确定最大值取法: ,解方程可得x的值;(3)利用正弦函数性质解三角不等式可得2kπ-π≤2x- ≤2kπ,即得x的取值范围.
试题解析:解:(1)由题意知=-=,∴T=π.
∴ω==2,由ω·+φ=0,得φ=-,又A=5,
∴y=5sin.
(2)函数的最大值为5,此时2x-=2kπ+ (k∈Z).∴x=kπ+ (k∈Z)
(3)∵5sin≤0,
∴2kπ-π≤2x-≤2kπ(k∈Z).
∴kπ-≤x≤kπ+ (k∈Z).
点睛:已知函数的图象求解析式
(1).
(2)由函数的周期求
(3)利用“五点法”中相对应的特殊点求
12.(1);(2);(3).
【解析】
试题分析:
(1)利用题意分别求得 可得函数的解析式为;
(2)利用题意结合二次型复合函数的性质可得实数的取值范围是;
(3)整理函数的解析式,结合角的范围可得函数的值域为.
试题解析:
(1)由图可知,,
,,,,
由于,故即.
。
(2),,即.
又,,
①当时,;
②当时,;
③当时,;
综上,实数的取值范围是
(3) ,
。
又,,,
即,
函数函数的值域为。
点睛:已知f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象求其解析式时,A比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:
(1)由即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0,则令ωx0+φ=0(或ωx0+φ=π),即可求出φ.
(2)代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.
13.(1);(2).
【分析】
(1)由周期求出,取点求出,进而得出的解析式;
(2)设,,解方程,得出,再由求出t的值.
【详解】
解:(1)由题意易知,周期,所以,所以.
将最高点代入中可得
得,即.
又因为,所以,所以.
(2)设,,则
所以
所以,所以,即
所以.
【点睛】
方法点睛:由图象求函数的解析式时,有如下步骤:
1、由最值得出的值;
2、由周期结合得出;
3、取点求出.
14.(1)见解析;(2)见解析
【解析】
【分析】
(1)通过实际问题得到与的函数关系为分段函数,从而判断出程序框填的结果.
(2)分类讨论时和时两种情形下的点Q坐标,从而得到答案.
【详解】
(1)当时,,
当时,
函数的解析式为,
故程序框图中①②处的函数关系式分别是,
(2)时,令,即,或,点的坐标为或
时,令,即,或,点的坐标为或
故点的坐标为
【点睛】
本题主要考查算法框图,三角函数的运用,意在考查学生的数形结合思想,分析实际问题的能力.
15.(1)1;(2)
【分析】
(1),利用三角函数的周期性可求ω的值.
(2)根据f(B)的值,求得B,由正弦定理求得A,最后求得C,利用向量的数量积公式求得答案.
【详解】
(1)
∵的最小正周期为,∴,∴.
(2)设△ABC中角A,B,C所对的边分别是a,b,c.
∵,∴,即,解得.
∵,∴,∵,∴,∴,,
∵,∴,,∴,∴.
【点睛】
本题主要考查了三角函数图象与性质,向量的数量积运算,三角函数恒等变换的应用.综合考查了学生分析问题和运算能力.
16.(1);(2).
【解析】
分析:(1)由表中的最大值和最小值可得的值,通过,可求,根据对称中心点坐标可知,图象过代入求解,可得函数的解析式;(2)结合函数图象:当时,函数的减区间是.
详解:由表中的最大值为3,最小值为﹣1,可得A=,
由=T,则T=2π.∴,
∵y=2sin(ωx+φ)的最大值是2,故得B=3﹣2=1.
此时函数f(x)=2sin(x+φ)+1.
∵图象过(﹣)带入可得:﹣1=2sin(+φ)+1,
可得:φ=﹣,(k∈Z).
解得:φ=,∵φ,∴φ=﹣.
故得函数f(x)的解析式为f(x)=2sin(x﹣)+1 .
(2)结合函数图象:当时,函数的减区间是.
点睛: 已知三角函数的性质求解析式的步骤:利用最值求出 ,利用最值点或零点的间隔先求出周期,用周期公式求出,利用特殊点求出,正确求是解题的关键.求解析时求参数是确定函数解析式的关键,由特殊点求时,一定要分清特殊点是“五点法”的第几个点.
17.(1);(2).
【分析】
(1)以点为坐标原点建立如图所示的平面直角坐标系,则,在中,设,又,故,,进而表示直线的方程,由直线与圆相切构建关系化简整理得,即可表示OA,OB,最后由三角形面积公式表示面积即可;
(2)令,则,由辅助角公式和三角函数值域可求得t的取值范围,进而对原面积的函数用含t的表达式换元,再令进行换元,并构建新的函数,由二次函数性质即可求得最小值.
【详解】
解:(1)以点为坐标原点建立如图所示的平面直角坐标系,则,在中,设,又,故,.
所以直线的方程为,即.
因为直线与圆相切,
所以.
因为点在直线的上方,
所以,
所以式可化为,解得.
所以,.
所以面积为.
(2)令,则,
且,
所以,.
令,,所以在上单调递减.
所以,当,即时,取得最大值,取最小值.
答:当时,面积为最小,政府投资最低.
【点睛】
本题考查三角函数的实际应用,应优先结合实际建立合适的数学模型,再按模型求最值,属于难题.
18.(1)最小正周期为,对称轴方程为;(2);(3).
【分析】
(1)由正弦型函数的周期公式可求得函数的最小正周期,解方程,可得出函数的对称轴方程;
(2)对实数的取值进行分类讨论,分析函数在区间上的单调性,求得、,即可求得的表达式;
(3)利用已知条件求得,分析可知函数在的值域是函数在的值域的子集,分、两种情况讨论,将问题转化为,综合可得出实数的取值范围.
【详解】
(1)函数的最小正周期为,
解方程,可得,
故函数的对称轴方程为;
(2)分以下几种情况讨论:
①当时,,,
当时,,
此时函数在区间上单调递减,在上单调递增,
所以,,,
则;
②当时,,,
当时,,
此时函数在区间上单调递减,在上单调递增,
所以,,,
则;
③当时,,,
当时,,
此时函数在上单调递增,则,,
则.
综上所述,;
(3)因为函数的最小正周期为,所以,,,
则,
所以,函数是以为周期的周期函数,研究函数的性质,只需研究函数在时的性质即可.
仿照(2)可得,
当时,;
当时,;
当时,.
所以,当时,,同理可知当时,.
作出函数的图象如下图所示:
所以,函数的值域为,
因为,则,所以,,
对任意的,存在,使得成立,
即函数在的值域是函数在的值域的子集,
因为.
当时,因为函数在上单调递减,在上单调递增,
所以,,
因为函数在上单调递增,
所以,,所以,,解得;
当时,因为函数在上单调递减,所以,,
,
所以,函数在上单调递减,在上单调递增,
所以,,所以,,即,
因为,则,令,则,
作出函数与函数的图象如下图所示:
有图可知,当时,;当时,.
此时,,解得.
综上所述,实数的取值范围是.
【点睛】
结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化:
一般地,已知函数,,,.
(1)若,,有成立,则;
(2)若,,有成立,则;
(3)若,,有成立,则;
(4)若,,有成立,则的值域是的值域的子集.
19.(1);(2)见解析
【分析】
(1)分子分母同除1,利用,把分母变形,然后分子分母同除 ,利用齐次式求,(2)利用辅助角公式把f(x)化为的形式,再利用正余弦函数的单调性求单调区间.
【详解】
(1)
,
(2)
周期为
由
可得
所以递增区间.
【点睛】
本题考查三角函数齐次式的应用,三角函数辅助角公式以及求单调区间,解题关键是转化为齐次式,属于基础题.
20.12小时后该城市开始受到台风的侵袭
【详解】
设在t时刻台风中心位于点Q,此时|OP|=300,|PQ|=20t,
台风侵袭范围的圆形区域半径为10t+60,
由,可知,
cos∠OPQ=cos(θ-45o)= cosθcos45o+sinθsin45o=
在 △OPQ中,由余弦定理,得
=
=
若城市O受到台风的侵袭,则有|OQ|≤r(t),即
,
整理,得,解得12≤t≤24,
答:12小时后该城市开始受到台风的侵袭.
21.0.5.
【分析】
先构造函数,求函数的定义域,根据函数的单调性可以确定函数零点的个数,取特殊值确定作为计算的初始区间,然后列表运用二分法求方程的近似解的方法,结合要求精确到,求出方程的近似解.
【详解】
令,函数的定义域为.
因为函数在上是增函数,所以至多有一个零点.
又因为,,所以方程在内有唯一一个实数解.
用二分法逐次计算,列表如下:
区间 中点的值 中点函数值(或近似值)
由于区间内的所有值,若精确到0.1,都是0.5,所以0.5是方程精确到0.1的近似解.
【点睛】
本题考查了二分法的应用. 本题中利用函数的单调性确定了初始区间,也可以在平面直角坐标系中画出函数与函数的图象,根据图象确定初始区间..
22.(1);(2).
【分析】
(1)根据图像可得振幅,最小正周期,则.
由,又,则易求得,即可得解.
(2)利用辅助角公式可得:
,再根据定义域即可得解.
【详解】
(1)由图象可得,
最小正周期,则.
由,
又,则易求得,
所以;
(2)由题意知,
所以
,
因为,所以,
所以.
【点睛】
本题考查了利用三角函数图像求解析式,考查了辅助角公式,在解题过程中注意各个量的对应关系,以及相关量的取值范围,整体难度不大,属于中档题.
23.
(1);
(2).
【分析】
(1)以圆心为原点,建立平面直角坐标系,利用三角函数的定义写出点的坐标,再代入进行求值;
(2)根据点在圆上运动的周期求出角速度,再写出与的函数解析式即可.
(1)
解:以圆心为原点,建立平面直角坐标系(如图所示),
则以为始边、为终边的角为,
故点的坐标为,
所以,
当时,
(米).
(2)
解:点在圆上转动的周期为60秒,
所以角速度为,
故秒转过的弧度数为,
所以与的函数解析式为:
().
24.(1)证明见解析;(2).
【分析】
(1)设,则,利用两点的斜率公式以及点在椭圆上可得定值;
(2)联立直线与椭圆方程,求出到的距离和到的距离,利用根与系数的关系可得面积的最大值.
【详解】
(1)证明:设,则,
∵,,∴,,
∵在椭圆上,∴
∴为定值.
(2)设,依题意:,点在第一象限,∴.
联立:得:,
∴,,
设到的距离为,到的距离为,
∴,,
∴.
又∵
(当时取等号),
∴.
∴四边形的面积的最大值为
25.(1);(2)
【分析】
(1)根据三角函数的图像可得以及周期,根据周期公式求出,再由求出即可求解.
(2)根据正弦函数的单调递增区间,整体代入解不等式即可.
【详解】
(1)由三角函数的图像可得,,
由,解得,
又,即,
所以,所以,
解得,
因为,所以,
所以.
(2)由(1),
则,
解得,
所以函数的单调增区间为.
【点睛】
本题考查了由三角函数的图像求解析式、求三角函数的单调区间,考查了基本运算求解能力,属于基础题.
26.(1)10;(2)18.
【分析】
(1)根据题意求出总价后可得优惠价;
(2)设是总价,据题意,在时,列出不等式,解之可得,注意分类讨论.
【详解】
(1)顾客一次购买松子和腰果各1千克,总价为元,支付元(元);
(2)设订单总价为,若,没有优惠,符合题意,
若,则,,而,所以,又,所以,最大值为.
27.(1);(2)变换情况见解析.
【分析】
(1)由求,由求,再代入点求,即可求得解析式;
(2)利用三角函数的图像变换可得解.
【详解】
(1)由图像知,解得,
由,,.
当时,,,又,,
所以所求函数解析式为.
(2)把函数图像上的所有点,向左平移个单位,得到图像,
然后把函数图像上的所有点,纵坐标保持不变,横坐标缩短为原来的,得到的图像,
再把函数图像上的所有点,横坐标保持不变,纵坐标变为原来的,得到的图像,
最后把函数图像上的所有点,向下平移1个单位,得到的图像.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
