5.2 平抛运动 同步练习(word版含答案)
文档属性
| 名称 | 5.2 平抛运动 同步练习(word版含答案) | 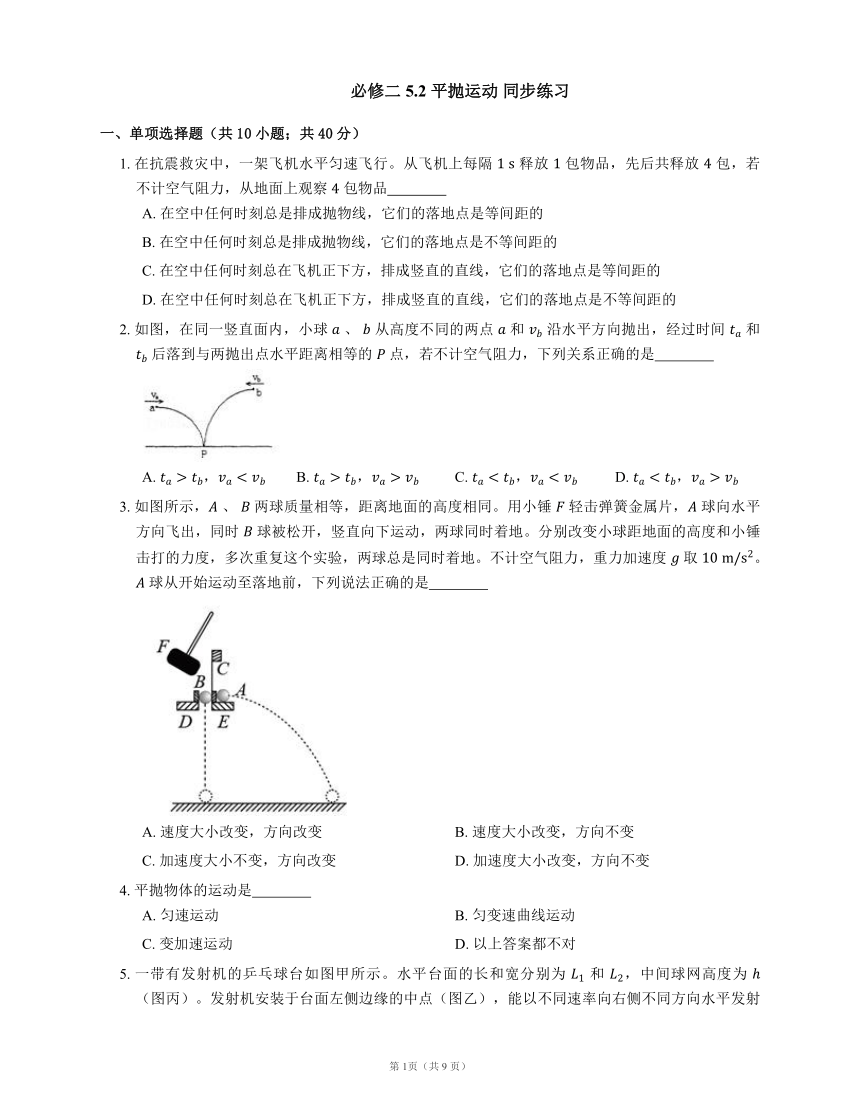 | |
| 格式 | docx | ||
| 文件大小 | 183.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-21 07:21:44 | ||
图片预览


文档简介
必修二 5.2 平抛运动 同步练习
一、单项选择题(共10小题;共40分)
1. 在抗震救灾中,一架飞机水平匀速飞行。从飞机上每隔 释放 包物品,先后共释放 包,若不计空气阻力,从地面上观察 包物品
A. 在空中任何时刻总是排成抛物线,它们的落地点是等间距的
B. 在空中任何时刻总是排成抛物线,它们的落地点是不等间距的
C. 在空中任何时刻总在飞机正下方,排成竖直的直线,它们的落地点是等间距的
D. 在空中任何时刻总在飞机正下方,排成竖直的直线,它们的落地点是不等间距的
2. 如图,在同一竖直面内,小球 、 从高度不同的两点 和 沿水平方向抛出,经过时间 和 后落到与两抛出点水平距离相等的 点,若不计空气阻力,下列关系正确的是
A. , B. , C. , D. ,
3. 如图所示, 、 两球质量相等,距离地面的高度相同。用小锤 轻击弹簧金属片, 球向水平方向飞出,同时 球被松开,竖直向下运动,两球同时着地。分别改变小球距地面的高度和小锤击打的力度,多次重复这个实验,两球总是同时着地。不计空气阻力,重力加速度 取 。 球从开始运动至落地前,下列说法正确的是
A. 速度大小改变,方向改变 B. 速度大小改变,方向不变
C. 加速度大小不变,方向改变 D. 加速度大小改变,方向不变
4. 平抛物体的运动是
A. 匀速运动 B. 匀变速曲线运动
C. 变加速运动 D. 以上答案都不对
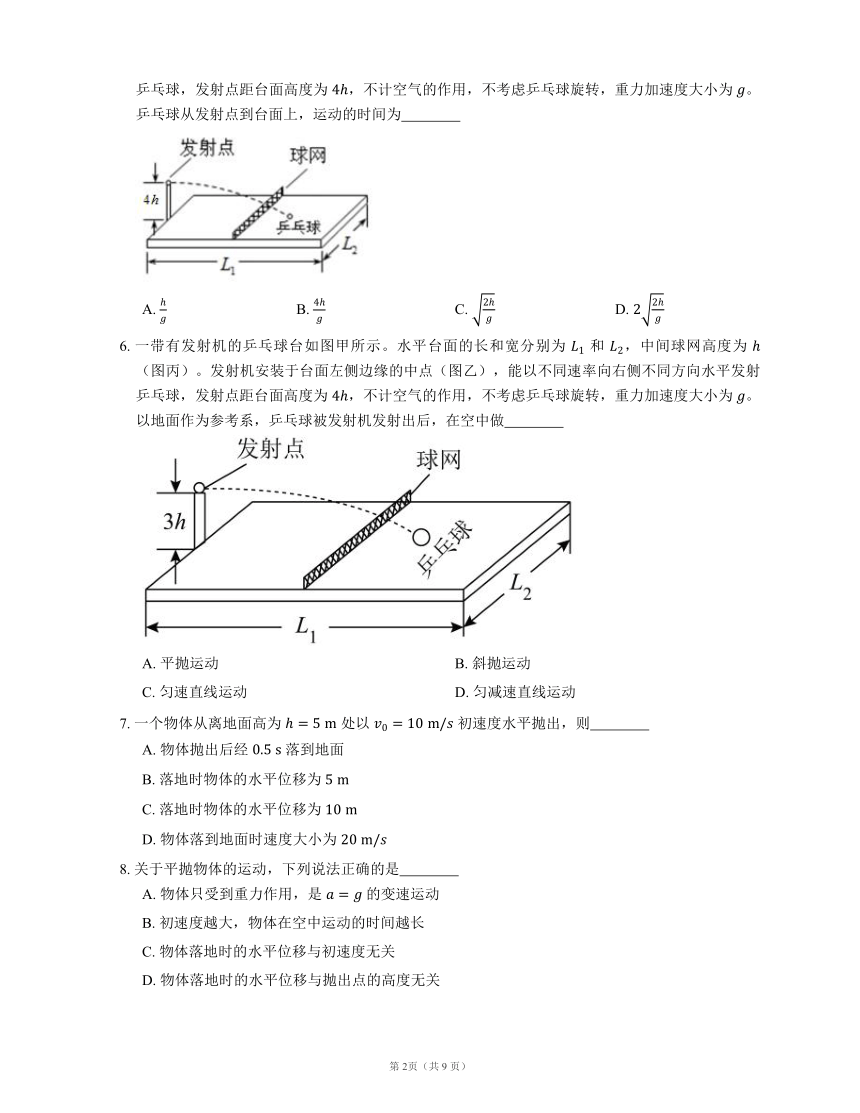
5. 一带有发射机的乒乓球台如图甲所示。水平台面的长和宽分别为 和 ,中间球网高度为 (图丙)。发射机安装于台面左侧边缘的中点(图乙),能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为 ,不计空气的作用,不考虑乒乓球旋转,重力加速度大小为 。乒乓球从发射点到台面上,运动的时间为
A. B. C. D.
6. 一带有发射机的乒乓球台如图甲所示。水平台面的长和宽分别为 和 ,中间球网高度为 (图丙)。发射机安装于台面左侧边缘的中点(图乙),能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为 ,不计空气的作用,不考虑乒乓球旋转,重力加速度大小为 。以地面作为参考系,乒乓球被发射机发射出后,在空中做
A. 平抛运动 B. 斜抛运动
C. 匀速直线运动 D. 匀减速直线运动
7. 一个物体从离地面高为 处以 初速度水平抛出,则
A. 物体抛出后经 落到地面
B. 落地时物体的水平位移为
C. 落地时物体的水平位移为
D. 物体落到地面时速度大小为
8. 关于平抛物体的运动,下列说法正确的是
A. 物体只受到重力作用,是 的变速运动
B. 初速度越大,物体在空中运动的时间越长
C. 物体落地时的水平位移与初速度无关
D. 物体落地时的水平位移与抛出点的高度无关
9. 铯原子钟是精确的计时仪器,图 中铯原子从 点以 的初速度在真空中做平抛运动,到达竖直平面 所用时间为 ;图 中铯原子在真空中从 点做竖直上抛运动,到达最高点 再返回 点,整个过程所用时间为 , 点到竖直平面 、 点到 点的距离均为 ,重力加速度取 ,则 为
A. B. C. D.
10. 如图所示,自水平地面上方高 处以速度 水平抛出一小球,小球到达地面时速度与水平方向的夹角为 。将小球移至高 处,以速度 水平抛出,小球到达地面时速度与水平方向的夹角也为 ,不计空气阻力,则 与 的关系为
A. B. C. D.
二、填空题(共5小题;共20分)
11. 平抛运动:初速度沿 方向的抛体运动。
12. 在距地面高 的低空有一小型飞机以 的速度水平飞行,假定从飞机上释放一物体, 取 ,不计空气阻力,那么物体落地时间是 ,它在下落过程中发生的水平位移是 ;落地前瞬间的速度大小为 。
13. 判断下列说法的正误。
平抛运动的物体初速度越大,下落得越快。
14. 用频闪照相技术拍下的两小球运动的频闪照片如图所示.拍摄时,光源的频闪频率为 , 球从 点水平抛出的同时, 球自 点开始下落,背景的小方格为相同的正方形.重力加速度 取 ,不计阻力.
(1)根据照片显示的信息,下列说法中正确的是 。
A.只能确定 球的运动是自由落体运动
B.不能确定 球沿竖直方向的运动是自由落体运动
C.只能确定 球沿水平方向的运动是匀速直线运动
D.可以断定 球的运动是水平方向的匀速直线运动和竖直方向的自由落体运动的合成
(2)根据照片信息可求出 球的水平速度大小为 ;当 球与 球运动了 时它们之间的距离最小.
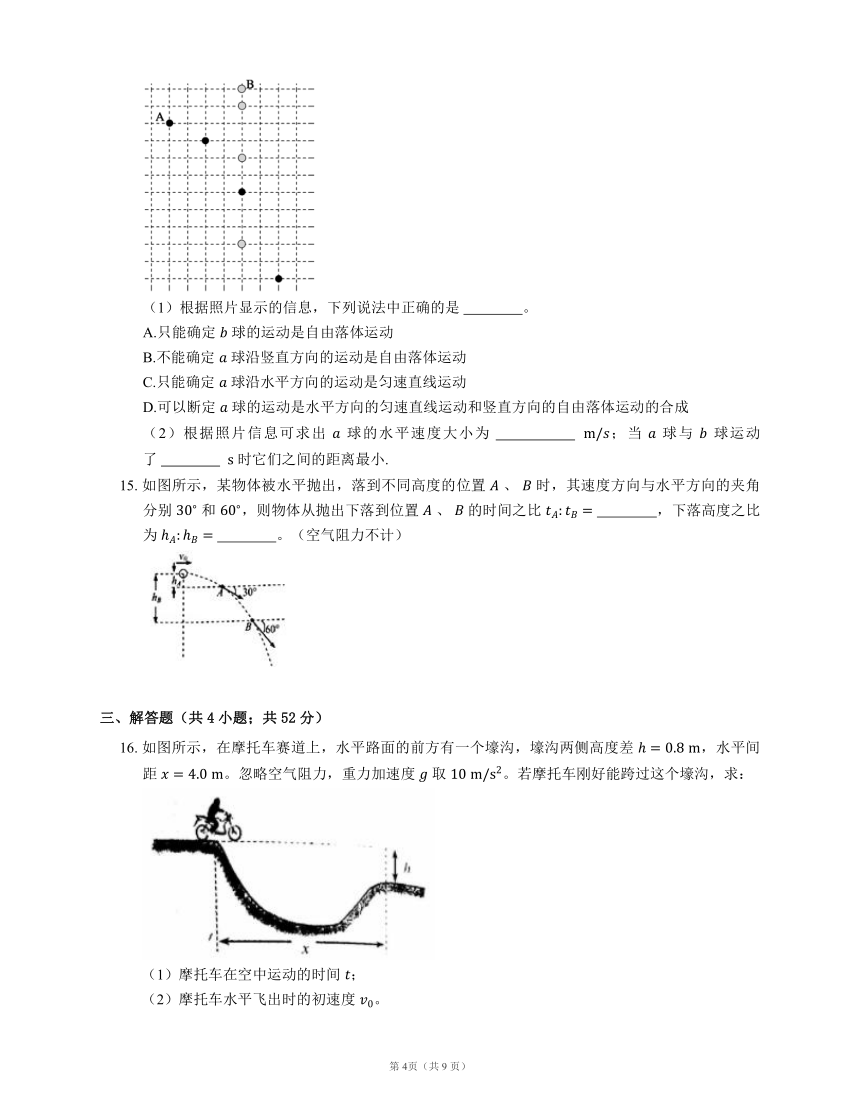
15. 如图所示,某物体被水平抛出,落到不同高度的位置 、 时,其速度方向与水平方向的夹角分别 和 ,则物体从抛出下落到位置 、 的时间之比 ,下落高度之比为 。(空气阻力不计)
三、解答题(共4小题;共52分)
16. 如图所示,在摩托车赛道上,水平路面的前方有一个壕沟,壕沟两侧高度差 ,水平间距 。忽略空气阻力,重力加速度 取 。若摩托车刚好能跨过这个壕沟,求:
(1)摩托车在空中运动的时间 ;
(2)摩托车水平飞出时的初速度 。
17. 把一小球从离地面高 处,以 的初速度水平抛出,不计空气阻力(),求:
(1)小球在空中飞行的时间;
(2)小球落地点离抛出点的水平距离;
(3)小球落地时的速度。
18. 一个物体从离地面 高的地方以 的速度水平抛出, 求:
(1)物体下落的时间;
(2)小球落地点离抛出点的水平距离;
(3)落地时的速度大小;
(4)落地时的速度方向。
19. 抛体运动在各类体育运动项目中很常见,如乒乓球运动。现讨论乒乓球发球问题,设球台长 、网高 ,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力。(设重力加速度为 )
(1)若球在球台边缘 点正上方高度为 处以速度 ,水平发出,落在球台的 点(如图实线所示),求 点距 点的距离 。
(2)若球在 点正上方以速度 水平发出,恰好在最高点时越过球网落在球台的 (如图虚线所示),求 的大小。
(3)若球在 正上方水平发出后,球经反弹恰好越过球网且刚好落在对方球台边缘 ,求发球点距 点的高度 。
答案
第一部分
1. C
【解析】因为不计空气阻力,物品在水平方向将保持和飞机一致的匀速运动,因而 包物品在空中任何时刻总在飞机正下方,排成竖直的直线;因为飞机高度一致,物品做平抛运动的时间一致,水平速度一致,间隔时间一致,所以它们的落地点是等间距的。
2. D
【解析】平抛运动的运动时间是由竖直的高度决定的,由于 的高度比 的小 ,
由于 的水平的位移相等,而 ,所以 ,所以D正确。
3. A
4. B
【解析】平抛运动的物体只受重力,轨迹为曲线,所以平抛运动的物体做匀变速曲线运动。
5. D
【解析】乒乓球做平抛运动,则竖直方向是自由落体运动,则
可得乒乓球从发射点到台面上,运动的时间为
故选D。
6. A
【解析】乒乓球被发射机发射出后,有水平方向的速度,竖直方向受到重力,因此在空中做平抛运动,故选A。
7. C
8. A
【解析】平抛运动的物体只受重力的作用,是 的匀变速运动,选项A正确;根据 可知,高度越大,物体在空中运动的时间越长,选项B错误;根据 可知,物体落地时的水平位移与初速度和抛出点的高度都有关,选项CD错误;故选A。
9. C
【解析】铯原子做平抛运动,水平方向上做匀速直线运动,即
,
解得 ,
铯原子做竖直上抛运动,抛至最高点用时 ,逆过程可视为自由落体,即
,
解得
,
则
。
10. B
【解析】小球做平抛运动,落地时:
第一种情况有:
第二种情况有:
联立两式解得:
第二部分
11. 水平
12. ;;
【解析】由 ,得:,代入数据得:,
水平位移 ,代入数据得:
,
,,
故 ,
代入数据得 。
13.
14. (1)D
(2)1;
【解析】(1)因为相邻两照片间的时间间隔相等,水平位移相等,知小球在水平方向上做匀速直线运动,竖直方向上的运动规律与 球运动规律相同,知竖直方向上做自由落体运动.
故D正确,A、B、C错误.故选D。
(2)根据
所以
所以平抛运动的初速度
因为两球在竖直方向上都做自由落体运动,所以竖直方向上位移之差恒定,当小球 运动到与 在同一竖直线上时,距离最短,则 。
15. ;
【解析】将 、 点速度分解
联立 得
在竖直方向,根据速度位移关系式有:
联立 得:
第三部分
16. (1)
【解析】物体在竖直方向上做自由落体运动,
解得
(2)
【解析】物体在水平方向上做匀速直线运动,
解得
17. (1)
【解析】根据 ,
小球飞行的时间 ;
(2)
【解析】落地点离抛出点的水平距离为 ;
(3) ,速度方向与水平方向的夹角为
【解析】小球落地时的竖直分速度为 ,
则小球落地时的速度大小为 ,
设落地时速度方向与水平方向的夹角为 ,则 ,
解得 。
18. (1)
【解析】平抛运动的物体在竖直方向上做自由落体运动,根据 得 。
(2)
【解析】水平距离为 。
(3)
【解析】落地时竖直分速度为 ,
所以落地时速度为 。
(4) 与水平方向夹角为
【解析】与水平方向夹角 的正切值为
得 。
19. (1)
【解析】设发球时飞行时间为 ,根据平抛运动有
解得 。
(2)
【解析】设发球高度为 ,飞行时间为 ,同理有
且
得 。
(3)
【解析】设球从恰好越过球网到最高点的时间为 ,水平距离为 ,根据抛体运动的特点及反弹的对称性,知反弹到最高点的水平位移为 。则反弹到越过球网的水平位移为 ,所以图中的 。在水平方向上做匀速直线运动,所以从越过球网到最高点所用的时间和从反弹到最高点的时间比为 。
对反弹到最高点的运动采取逆向思维,根据水平方向上的运动和竖直方向上的运动具有等时性,知越过球网到最高点竖直方向上的时间和反弹到最高点在竖直方向上的时间比为 。根据 得,知越过球网到最高点竖直方向上的位移和反弹到最高点的位移为 ,即 ,解得 。
第1页(共1 页)
一、单项选择题(共10小题;共40分)
1. 在抗震救灾中,一架飞机水平匀速飞行。从飞机上每隔 释放 包物品,先后共释放 包,若不计空气阻力,从地面上观察 包物品
A. 在空中任何时刻总是排成抛物线,它们的落地点是等间距的
B. 在空中任何时刻总是排成抛物线,它们的落地点是不等间距的
C. 在空中任何时刻总在飞机正下方,排成竖直的直线,它们的落地点是等间距的
D. 在空中任何时刻总在飞机正下方,排成竖直的直线,它们的落地点是不等间距的
2. 如图,在同一竖直面内,小球 、 从高度不同的两点 和 沿水平方向抛出,经过时间 和 后落到与两抛出点水平距离相等的 点,若不计空气阻力,下列关系正确的是
A. , B. , C. , D. ,
3. 如图所示, 、 两球质量相等,距离地面的高度相同。用小锤 轻击弹簧金属片, 球向水平方向飞出,同时 球被松开,竖直向下运动,两球同时着地。分别改变小球距地面的高度和小锤击打的力度,多次重复这个实验,两球总是同时着地。不计空气阻力,重力加速度 取 。 球从开始运动至落地前,下列说法正确的是
A. 速度大小改变,方向改变 B. 速度大小改变,方向不变
C. 加速度大小不变,方向改变 D. 加速度大小改变,方向不变
4. 平抛物体的运动是
A. 匀速运动 B. 匀变速曲线运动
C. 变加速运动 D. 以上答案都不对
5. 一带有发射机的乒乓球台如图甲所示。水平台面的长和宽分别为 和 ,中间球网高度为 (图丙)。发射机安装于台面左侧边缘的中点(图乙),能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为 ,不计空气的作用,不考虑乒乓球旋转,重力加速度大小为 。乒乓球从发射点到台面上,运动的时间为
A. B. C. D.
6. 一带有发射机的乒乓球台如图甲所示。水平台面的长和宽分别为 和 ,中间球网高度为 (图丙)。发射机安装于台面左侧边缘的中点(图乙),能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为 ,不计空气的作用,不考虑乒乓球旋转,重力加速度大小为 。以地面作为参考系,乒乓球被发射机发射出后,在空中做
A. 平抛运动 B. 斜抛运动
C. 匀速直线运动 D. 匀减速直线运动
7. 一个物体从离地面高为 处以 初速度水平抛出,则
A. 物体抛出后经 落到地面
B. 落地时物体的水平位移为
C. 落地时物体的水平位移为
D. 物体落到地面时速度大小为
8. 关于平抛物体的运动,下列说法正确的是
A. 物体只受到重力作用,是 的变速运动
B. 初速度越大,物体在空中运动的时间越长
C. 物体落地时的水平位移与初速度无关
D. 物体落地时的水平位移与抛出点的高度无关
9. 铯原子钟是精确的计时仪器,图 中铯原子从 点以 的初速度在真空中做平抛运动,到达竖直平面 所用时间为 ;图 中铯原子在真空中从 点做竖直上抛运动,到达最高点 再返回 点,整个过程所用时间为 , 点到竖直平面 、 点到 点的距离均为 ,重力加速度取 ,则 为
A. B. C. D.
10. 如图所示,自水平地面上方高 处以速度 水平抛出一小球,小球到达地面时速度与水平方向的夹角为 。将小球移至高 处,以速度 水平抛出,小球到达地面时速度与水平方向的夹角也为 ,不计空气阻力,则 与 的关系为
A. B. C. D.
二、填空题(共5小题;共20分)
11. 平抛运动:初速度沿 方向的抛体运动。
12. 在距地面高 的低空有一小型飞机以 的速度水平飞行,假定从飞机上释放一物体, 取 ,不计空气阻力,那么物体落地时间是 ,它在下落过程中发生的水平位移是 ;落地前瞬间的速度大小为 。
13. 判断下列说法的正误。
平抛运动的物体初速度越大,下落得越快。
14. 用频闪照相技术拍下的两小球运动的频闪照片如图所示.拍摄时,光源的频闪频率为 , 球从 点水平抛出的同时, 球自 点开始下落,背景的小方格为相同的正方形.重力加速度 取 ,不计阻力.
(1)根据照片显示的信息,下列说法中正确的是 。
A.只能确定 球的运动是自由落体运动
B.不能确定 球沿竖直方向的运动是自由落体运动
C.只能确定 球沿水平方向的运动是匀速直线运动
D.可以断定 球的运动是水平方向的匀速直线运动和竖直方向的自由落体运动的合成
(2)根据照片信息可求出 球的水平速度大小为 ;当 球与 球运动了 时它们之间的距离最小.
15. 如图所示,某物体被水平抛出,落到不同高度的位置 、 时,其速度方向与水平方向的夹角分别 和 ,则物体从抛出下落到位置 、 的时间之比 ,下落高度之比为 。(空气阻力不计)
三、解答题(共4小题;共52分)
16. 如图所示,在摩托车赛道上,水平路面的前方有一个壕沟,壕沟两侧高度差 ,水平间距 。忽略空气阻力,重力加速度 取 。若摩托车刚好能跨过这个壕沟,求:
(1)摩托车在空中运动的时间 ;
(2)摩托车水平飞出时的初速度 。
17. 把一小球从离地面高 处,以 的初速度水平抛出,不计空气阻力(),求:
(1)小球在空中飞行的时间;
(2)小球落地点离抛出点的水平距离;
(3)小球落地时的速度。
18. 一个物体从离地面 高的地方以 的速度水平抛出, 求:
(1)物体下落的时间;
(2)小球落地点离抛出点的水平距离;
(3)落地时的速度大小;
(4)落地时的速度方向。
19. 抛体运动在各类体育运动项目中很常见,如乒乓球运动。现讨论乒乓球发球问题,设球台长 、网高 ,乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力。(设重力加速度为 )
(1)若球在球台边缘 点正上方高度为 处以速度 ,水平发出,落在球台的 点(如图实线所示),求 点距 点的距离 。
(2)若球在 点正上方以速度 水平发出,恰好在最高点时越过球网落在球台的 (如图虚线所示),求 的大小。
(3)若球在 正上方水平发出后,球经反弹恰好越过球网且刚好落在对方球台边缘 ,求发球点距 点的高度 。
答案
第一部分
1. C
【解析】因为不计空气阻力,物品在水平方向将保持和飞机一致的匀速运动,因而 包物品在空中任何时刻总在飞机正下方,排成竖直的直线;因为飞机高度一致,物品做平抛运动的时间一致,水平速度一致,间隔时间一致,所以它们的落地点是等间距的。
2. D
【解析】平抛运动的运动时间是由竖直的高度决定的,由于 的高度比 的小 ,
由于 的水平的位移相等,而 ,所以 ,所以D正确。
3. A
4. B
【解析】平抛运动的物体只受重力,轨迹为曲线,所以平抛运动的物体做匀变速曲线运动。
5. D
【解析】乒乓球做平抛运动,则竖直方向是自由落体运动,则
可得乒乓球从发射点到台面上,运动的时间为
故选D。
6. A
【解析】乒乓球被发射机发射出后,有水平方向的速度,竖直方向受到重力,因此在空中做平抛运动,故选A。
7. C
8. A
【解析】平抛运动的物体只受重力的作用,是 的匀变速运动,选项A正确;根据 可知,高度越大,物体在空中运动的时间越长,选项B错误;根据 可知,物体落地时的水平位移与初速度和抛出点的高度都有关,选项CD错误;故选A。
9. C
【解析】铯原子做平抛运动,水平方向上做匀速直线运动,即
,
解得 ,
铯原子做竖直上抛运动,抛至最高点用时 ,逆过程可视为自由落体,即
,
解得
,
则
。
10. B
【解析】小球做平抛运动,落地时:
第一种情况有:
第二种情况有:
联立两式解得:
第二部分
11. 水平
12. ;;
【解析】由 ,得:,代入数据得:,
水平位移 ,代入数据得:
,
,,
故 ,
代入数据得 。
13.
14. (1)D
(2)1;
【解析】(1)因为相邻两照片间的时间间隔相等,水平位移相等,知小球在水平方向上做匀速直线运动,竖直方向上的运动规律与 球运动规律相同,知竖直方向上做自由落体运动.
故D正确,A、B、C错误.故选D。
(2)根据
所以
所以平抛运动的初速度
因为两球在竖直方向上都做自由落体运动,所以竖直方向上位移之差恒定,当小球 运动到与 在同一竖直线上时,距离最短,则 。
15. ;
【解析】将 、 点速度分解
联立 得
在竖直方向,根据速度位移关系式有:
联立 得:
第三部分
16. (1)
【解析】物体在竖直方向上做自由落体运动,
解得
(2)
【解析】物体在水平方向上做匀速直线运动,
解得
17. (1)
【解析】根据 ,
小球飞行的时间 ;
(2)
【解析】落地点离抛出点的水平距离为 ;
(3) ,速度方向与水平方向的夹角为
【解析】小球落地时的竖直分速度为 ,
则小球落地时的速度大小为 ,
设落地时速度方向与水平方向的夹角为 ,则 ,
解得 。
18. (1)
【解析】平抛运动的物体在竖直方向上做自由落体运动,根据 得 。
(2)
【解析】水平距离为 。
(3)
【解析】落地时竖直分速度为 ,
所以落地时速度为 。
(4) 与水平方向夹角为
【解析】与水平方向夹角 的正切值为
得 。
19. (1)
【解析】设发球时飞行时间为 ,根据平抛运动有
解得 。
(2)
【解析】设发球高度为 ,飞行时间为 ,同理有
且
得 。
(3)
【解析】设球从恰好越过球网到最高点的时间为 ,水平距离为 ,根据抛体运动的特点及反弹的对称性,知反弹到最高点的水平位移为 。则反弹到越过球网的水平位移为 ,所以图中的 。在水平方向上做匀速直线运动,所以从越过球网到最高点所用的时间和从反弹到最高点的时间比为 。
对反弹到最高点的运动采取逆向思维,根据水平方向上的运动和竖直方向上的运动具有等时性,知越过球网到最高点竖直方向上的时间和反弹到最高点在竖直方向上的时间比为 。根据 得,知越过球网到最高点竖直方向上的位移和反弹到最高点的位移为 ,即 ,解得 。
第1页(共1 页)
