人教版九下 26.2 实际问题与反比例函数 第1课时(word版含答案)
文档属性
| 名称 | 人教版九下 26.2 实际问题与反比例函数 第1课时(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 359.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 17:01:56 | ||
图片预览


文档简介
九下_第26章 反比例函数_26.2 实际问题与反比例函数(第1课时)
一、选择题(共4小题;共20分)
1. 当路程 一定时,速度 与时间 之间的函数关系是
A. 正比例函数 B. 反比例函数 C. 一次函数 D. 二次函数
2. 已知圆柱的侧面积是 ,若圆柱的底面半径为 ,高为 ,则 与 的函数关系图象大致是下图中的
A. B.
C. D.
3. 某村的粮食产量为 吨( 为常数),该村平均每人占有粮食 吨,人口数为 ,则 与 之间的函数关系图象为下图中的
A. B.
C. D.
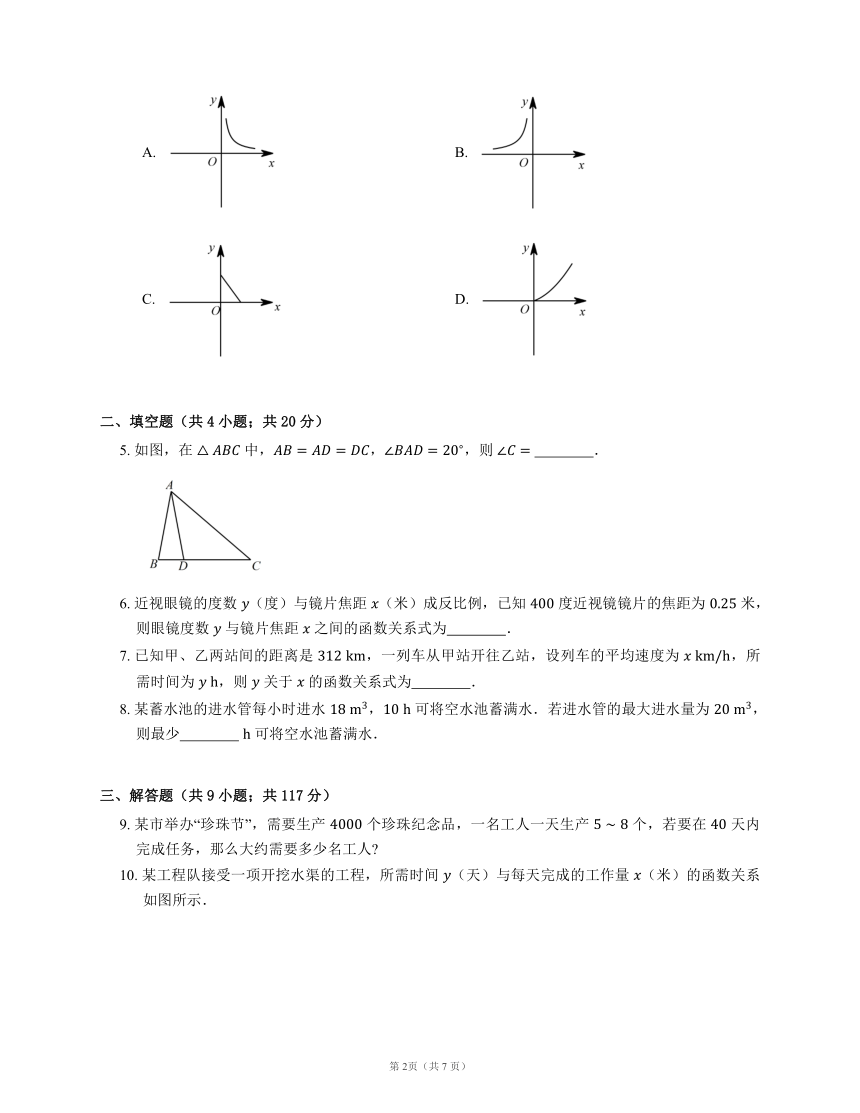
4. 某市一数学课外兴趣小组的同学每人制作了一个面积为 的长方形学具进行展示,设长方形的宽为 ,长为 ,那么这些同学所制作的长方形的长 与宽 之间的函数关系的图象大致是下图中的
A. B.
C. D.
二、填空题(共4小题;共20分)
5. 如图,在 中,,,则 .
6. 近视眼镜的度数 (度)与镜片焦距 (米)成反比例,已知 度近视镜镜片的焦距为 米,则眼镜度数 与镜片焦距 之间的函数关系式为 .
7. 已知甲、乙两站间的距离是 ,一列车从甲站开往乙站,设列车的平均速度为 ,所需时间为 ,则 关于 的函数关系式为 .
8. 某蓄水池的进水管每小时进水 , 可将空水池蓄满水.若进水管的最大进水量为 ,则最少 可将空水池蓄满水.
三、解答题(共9小题;共117分)
9. 某市举办“珍珠节”,需要生产 个珍珠纪念品,一名工人一天生产 个,若要在 天内完成任务,那么大约需要多少名工人
10. 某工程队接受一项开挖水渠的工程,所需时间 (天)与每天完成的工作量 (米)的函数关系如图所示.
(1)共需开挖水渠多少米
(2)如果为了防汛工作的需要,必须在 天内完成任务,那么每天至少完成多少米 (结果保留一位小数)
11. 将油箱注满 升油后,轿车可行驶的总路程 (千米) 与平均耗油量 (升/千米) 之间是反比例函数关系 ( 是常数,).已知某轿车油箱注满油后,以平均耗油量为每千米 升的速度行驶,可行驶 千米.
(1)求该轿车可行驶的总路程 与平均耗油量 之间的函数解析式.
(2)当平均耗油量为 升/千米时,该轿车可以行驶多少千米
12. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.如图所示是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 变化的函数图象,其中 段是双曲线 的一部分.根据图中的信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为 的时间有多少小时
(2)求 的值.
(3)当 时,大棚内的温度为多少摄氏度
13. 一辆汽车从甲地开往乙地,随着汽车的平均速度 的变化,所需时间 的变化情况如图所示.
(1)甲、乙两地相距多少千米
(2)写出 与 之间的函数关系式.
(3)当汽车的平均速度为 时,所需时间为多少
(4)如果准备 内(含 )到达,那么汽车的平均速度至少为多少
14. 某空调厂的装配车间计划组装 台空调.
(1)从组装空调开始,每天组装的台数 (单位:台/天)与生产的时间 (单位:天)之间有怎样的函数关系
(2)原计划用 个月时间(每月以 天计算)完成,由于气温提前升高,厂家决定这批空调提前 天上市,那么装配车间每天至少要组装多少台空调
15. 客运总站售票大厅为方便旅客购票,同时又节约成本,常根据客流量决定开放售票窗口数,假定每个窗口平均每小时可以售票 张,开放 个售票窗口时,需要 个小时才能使当天购票的旅客全部买到票.
(1)当天一共售出多少张票
(2)设开放 个售票窗口时,需要 小时才能使当天购票的旅客全部买到票,试求出 与 之间的函数关系式.
(3)如果准备在 小时内使当天购票的旅客全部买到票,那么至少要开放几个售票窗口
16. 某商场出售一批进价为 元的贺卡,在市场营销中发现,这种商品的日销售单价 (元)与日销售量 (个)之间的关系如下:
(1)根据表中数据在平面直角坐标系中描出实数对 的对应点;
(2)猜测并确定 与 之间的函数关系式;
(3)设经营这种贺卡的销售利润为 元,试求出 与 之间的函数关系式.若物价局规定这种贺卡的售价不能超过 元/个,请你求出当日销售单价定为多少元时,才能获得最大日销售利润.
17. 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 (毫克)与时间 (时)成正比,药物释放完毕后, 与 的函数关系式为 ( 为常数),如图所示.根据图中提供的信息解答下列问题:
(1)写出从药物释放开始, 与 之间的两个函数关系式及相应的自变量的取值范围.
(2)据测定,当空气中每立方米的含药量降低到 毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时,学生才能进入教室
答案
第一部分
1. B
2. C
3. D
4. A
第二部分
5.
【解析】,,
.
是 的外角,
.
.
.
6.
7.
8.
【解析】蓄水池的最大蓄水量为 ,.
第三部分
9. 设需要工人 名,每人每天生产 个,
根据题意,得
即
因为 ,所以 ,即 .
因为 是正整数,所以大约需要 名工人.
10. (1) 设 .
因为当 时,,
所以 ,所以 ,
所以共需开挖水渠 米.
(2) 当 时,,则 ,
所以每天至少完成约 米.
11. (1) 由题意知 (升).
所以 .
(2) 当 时,.
因此该轿车可以行驶 千米.
12. (1) 恒温系统在这天保持大棚内温度为 的时间有 .
(2) 点 在双曲线 上,
,
.
(3) 当 时,,
当 时,大棚内的温度为 .
13. (1) 设甲、乙两地相距 .
由题图知 ,
把 , 代入,得 ,
.
故甲、乙两地相距 .
(2) 由()知 .
(3) 把 代入 ,得 .
故当汽车的平均速度为 时,所需时间为 .
(4) 当 时,代入 中,得 .
故汽车的平均速度至少为 时,可在 内到达.
14. (1) 由题意,得 .
(2) 把 代入,得 .
故每天至少组装 台空调,方可提前 天上市.
15. (1) 当天一共售票数为 (张).
(2) 根据题意有 ,
.
(3) 当 时,,
即至少要开放 个售票窗口.
16. (1) 描点如图.
(2) 根据图象猜测 与 成反比例函数关系.设 ,把点 的坐标代入 ,得 .
所以 .
把点 ,, 的坐标代入上式均成立.
所以 与 之间的函数关系式为 .
(3) .
当 时, 有最大值,
故当日销售单价定为 元时,才能获得最大日销售利润.
17. (1) 将点 的坐标代入函数关系式 ,解得 ,
,
将 代入 ,得 ,
药物释放完毕后, 与 的函数关系式为 ,
设药物释放过程中, 与 的函数关系式为 ,
将点 的坐标代入 ,得 ,
药物释放过程中, 与 的函数关系式为 .
(2) 解不等式 ,得 ,
至少需要经过 小时,学生才能进入教室.
第1页(共1 页)
一、选择题(共4小题;共20分)
1. 当路程 一定时,速度 与时间 之间的函数关系是
A. 正比例函数 B. 反比例函数 C. 一次函数 D. 二次函数
2. 已知圆柱的侧面积是 ,若圆柱的底面半径为 ,高为 ,则 与 的函数关系图象大致是下图中的
A. B.
C. D.
3. 某村的粮食产量为 吨( 为常数),该村平均每人占有粮食 吨,人口数为 ,则 与 之间的函数关系图象为下图中的
A. B.
C. D.
4. 某市一数学课外兴趣小组的同学每人制作了一个面积为 的长方形学具进行展示,设长方形的宽为 ,长为 ,那么这些同学所制作的长方形的长 与宽 之间的函数关系的图象大致是下图中的
A. B.
C. D.
二、填空题(共4小题;共20分)
5. 如图,在 中,,,则 .
6. 近视眼镜的度数 (度)与镜片焦距 (米)成反比例,已知 度近视镜镜片的焦距为 米,则眼镜度数 与镜片焦距 之间的函数关系式为 .
7. 已知甲、乙两站间的距离是 ,一列车从甲站开往乙站,设列车的平均速度为 ,所需时间为 ,则 关于 的函数关系式为 .
8. 某蓄水池的进水管每小时进水 , 可将空水池蓄满水.若进水管的最大进水量为 ,则最少 可将空水池蓄满水.
三、解答题(共9小题;共117分)
9. 某市举办“珍珠节”,需要生产 个珍珠纪念品,一名工人一天生产 个,若要在 天内完成任务,那么大约需要多少名工人
10. 某工程队接受一项开挖水渠的工程,所需时间 (天)与每天完成的工作量 (米)的函数关系如图所示.
(1)共需开挖水渠多少米
(2)如果为了防汛工作的需要,必须在 天内完成任务,那么每天至少完成多少米 (结果保留一位小数)
11. 将油箱注满 升油后,轿车可行驶的总路程 (千米) 与平均耗油量 (升/千米) 之间是反比例函数关系 ( 是常数,).已知某轿车油箱注满油后,以平均耗油量为每千米 升的速度行驶,可行驶 千米.
(1)求该轿车可行驶的总路程 与平均耗油量 之间的函数解析式.
(2)当平均耗油量为 升/千米时,该轿车可以行驶多少千米
12. 我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为 的条件下生长最快的新品种.如图所示是某天恒温系统从开启到关闭及关闭后,大棚内温度 随时间 变化的函数图象,其中 段是双曲线 的一部分.根据图中的信息解答下列问题:
(1)恒温系统在这天保持大棚内温度为 的时间有多少小时
(2)求 的值.
(3)当 时,大棚内的温度为多少摄氏度
13. 一辆汽车从甲地开往乙地,随着汽车的平均速度 的变化,所需时间 的变化情况如图所示.
(1)甲、乙两地相距多少千米
(2)写出 与 之间的函数关系式.
(3)当汽车的平均速度为 时,所需时间为多少
(4)如果准备 内(含 )到达,那么汽车的平均速度至少为多少
14. 某空调厂的装配车间计划组装 台空调.
(1)从组装空调开始,每天组装的台数 (单位:台/天)与生产的时间 (单位:天)之间有怎样的函数关系
(2)原计划用 个月时间(每月以 天计算)完成,由于气温提前升高,厂家决定这批空调提前 天上市,那么装配车间每天至少要组装多少台空调
15. 客运总站售票大厅为方便旅客购票,同时又节约成本,常根据客流量决定开放售票窗口数,假定每个窗口平均每小时可以售票 张,开放 个售票窗口时,需要 个小时才能使当天购票的旅客全部买到票.
(1)当天一共售出多少张票
(2)设开放 个售票窗口时,需要 小时才能使当天购票的旅客全部买到票,试求出 与 之间的函数关系式.
(3)如果准备在 小时内使当天购票的旅客全部买到票,那么至少要开放几个售票窗口
16. 某商场出售一批进价为 元的贺卡,在市场营销中发现,这种商品的日销售单价 (元)与日销售量 (个)之间的关系如下:
(1)根据表中数据在平面直角坐标系中描出实数对 的对应点;
(2)猜测并确定 与 之间的函数关系式;
(3)设经营这种贺卡的销售利润为 元,试求出 与 之间的函数关系式.若物价局规定这种贺卡的售价不能超过 元/个,请你求出当日销售单价定为多少元时,才能获得最大日销售利润.
17. 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 (毫克)与时间 (时)成正比,药物释放完毕后, 与 的函数关系式为 ( 为常数),如图所示.根据图中提供的信息解答下列问题:
(1)写出从药物释放开始, 与 之间的两个函数关系式及相应的自变量的取值范围.
(2)据测定,当空气中每立方米的含药量降低到 毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时,学生才能进入教室
答案
第一部分
1. B
2. C
3. D
4. A
第二部分
5.
【解析】,,
.
是 的外角,
.
.
.
6.
7.
8.
【解析】蓄水池的最大蓄水量为 ,.
第三部分
9. 设需要工人 名,每人每天生产 个,
根据题意,得
即
因为 ,所以 ,即 .
因为 是正整数,所以大约需要 名工人.
10. (1) 设 .
因为当 时,,
所以 ,所以 ,
所以共需开挖水渠 米.
(2) 当 时,,则 ,
所以每天至少完成约 米.
11. (1) 由题意知 (升).
所以 .
(2) 当 时,.
因此该轿车可以行驶 千米.
12. (1) 恒温系统在这天保持大棚内温度为 的时间有 .
(2) 点 在双曲线 上,
,
.
(3) 当 时,,
当 时,大棚内的温度为 .
13. (1) 设甲、乙两地相距 .
由题图知 ,
把 , 代入,得 ,
.
故甲、乙两地相距 .
(2) 由()知 .
(3) 把 代入 ,得 .
故当汽车的平均速度为 时,所需时间为 .
(4) 当 时,代入 中,得 .
故汽车的平均速度至少为 时,可在 内到达.
14. (1) 由题意,得 .
(2) 把 代入,得 .
故每天至少组装 台空调,方可提前 天上市.
15. (1) 当天一共售票数为 (张).
(2) 根据题意有 ,
.
(3) 当 时,,
即至少要开放 个售票窗口.
16. (1) 描点如图.
(2) 根据图象猜测 与 成反比例函数关系.设 ,把点 的坐标代入 ,得 .
所以 .
把点 ,, 的坐标代入上式均成立.
所以 与 之间的函数关系式为 .
(3) .
当 时, 有最大值,
故当日销售单价定为 元时,才能获得最大日销售利润.
17. (1) 将点 的坐标代入函数关系式 ,解得 ,
,
将 代入 ,得 ,
药物释放完毕后, 与 的函数关系式为 ,
设药物释放过程中, 与 的函数关系式为 ,
将点 的坐标代入 ,得 ,
药物释放过程中, 与 的函数关系式为 .
(2) 解不等式 ,得 ,
至少需要经过 小时,学生才能进入教室.
第1页(共1 页)
