人教版九年级数学下册27.2.2 相似三角形的性质同步练习 (word版含答案)
文档属性
| 名称 | 人教版九年级数学下册27.2.2 相似三角形的性质同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 408.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 17:59:28 | ||
图片预览

文档简介
九下_第27章 相似_27.2 相似三角形_27.2.2 相似三角形的性质
一、选择题(共2小题;共10分)
1. 如图所示是一束平行的太阳光从教室窗户 射入的平面示意图,光线与地面所成角 , 在教室地面的影长 ,若窗户的下沿到教室地面的距离 ,则窗户的上沿到教室地面的距离 为
A. B. C. D.
2. 如图所示,小明在 时测得某树的影长为 , 时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为
A. B. C. D.
二、填空题(共6小题;共30分)
3. 如图,在 中,,,则 .
4. 一斜坡长 ,高为 ,将一重物从斜坡下起点处推到斜坡上 处停下,停下地点的高度为 .
5. 如图,小明在打网球时使球恰好能过网,而且落在离网 的位置上,则球拍击球的高度 为 .
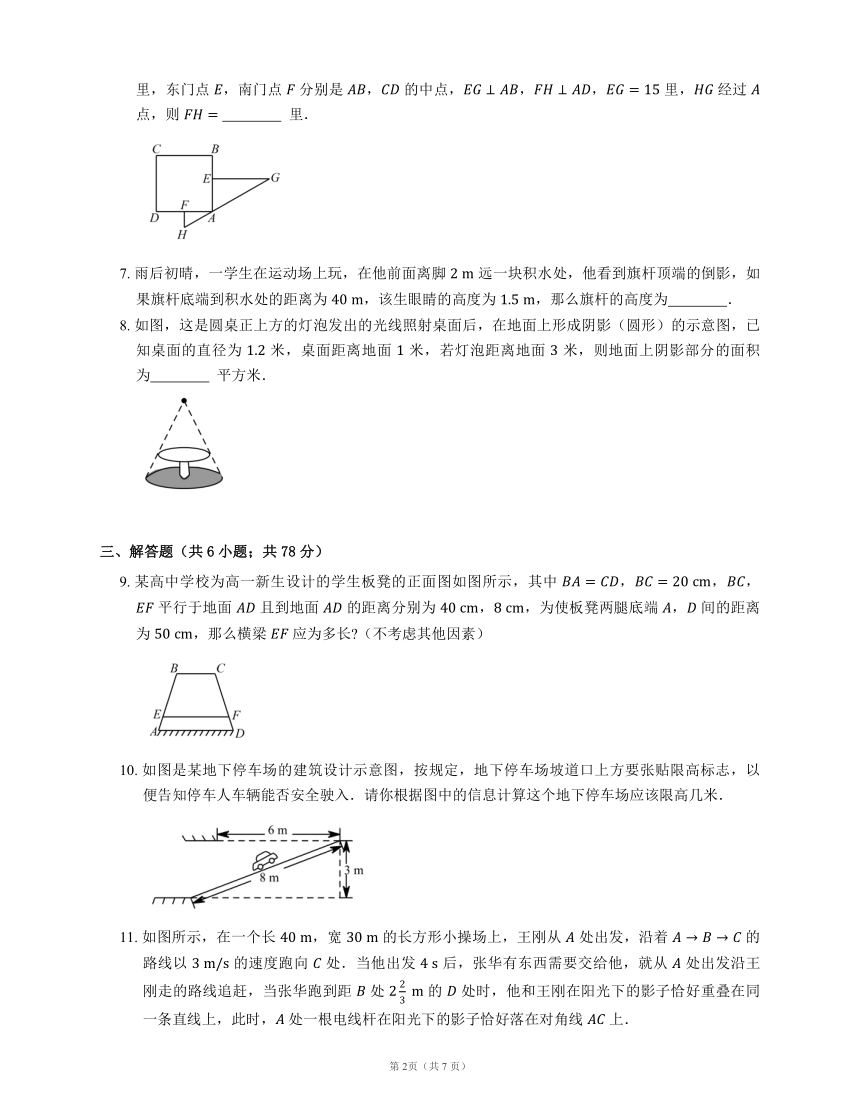
6. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木 ”这句话摘自《九章算术》,意思是说:如图,矩形 ,东边城墙 长 里,南边城墙 长 里,东门点 ,南门点 分别是 , 的中点,,, 里, 经过 点,则 里.
7. 雨后初晴,一学生在运动场上玩,在他前面离脚 远一块积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为 ,该生眼睛的高度为 ,那么旗杆的高度为 .
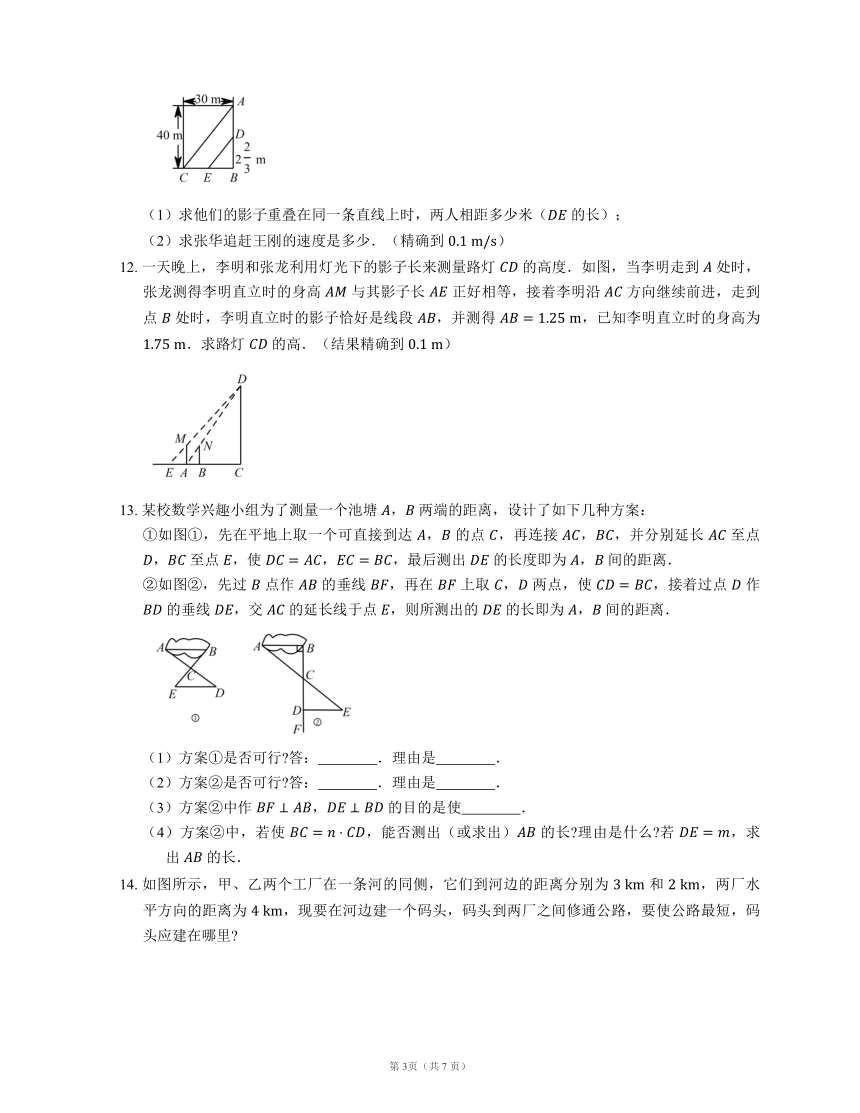
8. 如图,这是圆桌正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为 米,桌面距离地面 米,若灯泡距离地面 米,则地面上阴影部分的面积为 平方米.
三、解答题(共6小题;共78分)
9. 某高中学校为高一新生设计的学生板凳的正面图如图所示,其中 ,,, 平行于地面 且到地面 的距离分别为 ,,为使板凳两腿底端 , 间的距离为 ,那么横梁 应为多长 (不考虑其他因素)
10. 如图是某地下停车场的建筑设计示意图,按规定,地下停车场坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入.请你根据图中的信息计算这个地下停车场应该限高几米.
11. 如图所示,在一个长 ,宽 的长方形小操场上,王刚从 处出发,沿着 的路线以 的速度跑向 处.当他出发 后,张华有东西需要交给他,就从 处出发沿王刚走的路线追赶,当张华跑到距 处 的 处时,他和王刚在阳光下的影子恰好重叠在同一条直线上,此时, 处一根电线杆在阳光下的影子恰好落在对角线 上.
(1)求他们的影子重叠在同一条直线上时,两人相距多少米( 的长);
(2)求张华追赶王刚的速度是多少.(精确到 )
12. 一天晚上,李明和张龙利用灯光下的影子长来测量路灯 的高度.如图,当李明走到 处时,张龙测得李明直立时的身高 与其影子长 正好相等,接着李明沿 方向继续前进,走到点 处时,李明直立时的影子恰好是线段 ,并测得 ,已知李明直立时的身高为 .求路灯 的高.(结果精确到 )
13. 某校数学兴趣小组为了测量一个池塘 , 两端的距离,设计了如下几种方案:
①如图①,先在平地上取一个可直接到达 , 的点 ,再连接 ,,并分别延长 至点 , 至点 ,使 ,,最后测出 的长度即为 , 间的距离.
②如图②,先过 点作 的垂线 ,再在 上取 , 两点,使 ,接着过点 作 的垂线 ,交 的延长线于点 ,则所测出的 的长即为 , 间的距离.
(1)方案①是否可行 答: .理由是 .
(2)方案②是否可行 答: .理由是 .
(3)方案②中作 , 的目的是使 .
(4)方案②中,若使 ,能否测出(或求出) 的长 理由是什么 若 ,求出 的长.
14. 如图所示,甲、乙两个工厂在一条河的同侧,它们到河边的距离分别为 和 ,两厂水平方向的距离为 ,现要在河边建一个码头,码头到两厂之间修通公路,要使公路最短,码头应建在哪里
答案
第一部分
1. B
2. B
第二部分
3.
【解析】,,
.
是 的外角,
.
.
.
4.
5.
【解析】由题意知 ,解得 .
6.
【解析】由题意知 ,
,
(里).
7.
【解析】设旗杆的高度为 ,则 ,解得 .
8.
第三部分
9. 过点 作 ,交 于 ,交 于 ,过点 作 于点 ,则 ,设垂足为 .
则 ,
.
由题意知 ,.
,
.
,
即 ,
解得 .
,
即横梁 的长为 .
10. 过 作 ,如图.
,
.
又 ,
,
.
又 ,,.
.
地下停车场应该限高 .
11. (1) 由题意知 ,
所以 ,
所以 .
在 中,,
而 ,,
所以 .
(2) 由()知 ,王刚到达 处所用的时间为 .
张华到达 处所用时间为 .
所以张华追赶王刚的速度为 .
12. 设 的高为 .
,,,
,.
,
.
由 得 ,
,即 ,解得 .
路灯 的高约为 .
13. (1) 可行;由 ,得
(2) 可行;由 ,得
(3)
(4) 能.
理由:
,
,
,
而 ,即 ,
.
若 ,则 .
14. 如图,延长 到 ,使 ,连接 交 于点 ,
则码头应建在点 处.
设 ,则 .
,,
,
,即 ,解得 ,即 .
故码头应建在距 点 的点 处.
第1页(共1 页)
一、选择题(共2小题;共10分)
1. 如图所示是一束平行的太阳光从教室窗户 射入的平面示意图,光线与地面所成角 , 在教室地面的影长 ,若窗户的下沿到教室地面的距离 ,则窗户的上沿到教室地面的距离 为
A. B. C. D.
2. 如图所示,小明在 时测得某树的影长为 , 时又测得该树的影长为 ,若两次日照的光线互相垂直,则树的高度为
A. B. C. D.
二、填空题(共6小题;共30分)
3. 如图,在 中,,,则 .
4. 一斜坡长 ,高为 ,将一重物从斜坡下起点处推到斜坡上 处停下,停下地点的高度为 .
5. 如图,小明在打网球时使球恰好能过网,而且落在离网 的位置上,则球拍击球的高度 为 .
6. “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木 ”这句话摘自《九章算术》,意思是说:如图,矩形 ,东边城墙 长 里,南边城墙 长 里,东门点 ,南门点 分别是 , 的中点,,, 里, 经过 点,则 里.
7. 雨后初晴,一学生在运动场上玩,在他前面离脚 远一块积水处,他看到旗杆顶端的倒影,如果旗杆底端到积水处的距离为 ,该生眼睛的高度为 ,那么旗杆的高度为 .
8. 如图,这是圆桌正上方的灯泡发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图,已知桌面的直径为 米,桌面距离地面 米,若灯泡距离地面 米,则地面上阴影部分的面积为 平方米.
三、解答题(共6小题;共78分)
9. 某高中学校为高一新生设计的学生板凳的正面图如图所示,其中 ,,, 平行于地面 且到地面 的距离分别为 ,,为使板凳两腿底端 , 间的距离为 ,那么横梁 应为多长 (不考虑其他因素)
10. 如图是某地下停车场的建筑设计示意图,按规定,地下停车场坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入.请你根据图中的信息计算这个地下停车场应该限高几米.
11. 如图所示,在一个长 ,宽 的长方形小操场上,王刚从 处出发,沿着 的路线以 的速度跑向 处.当他出发 后,张华有东西需要交给他,就从 处出发沿王刚走的路线追赶,当张华跑到距 处 的 处时,他和王刚在阳光下的影子恰好重叠在同一条直线上,此时, 处一根电线杆在阳光下的影子恰好落在对角线 上.
(1)求他们的影子重叠在同一条直线上时,两人相距多少米( 的长);
(2)求张华追赶王刚的速度是多少.(精确到 )
12. 一天晚上,李明和张龙利用灯光下的影子长来测量路灯 的高度.如图,当李明走到 处时,张龙测得李明直立时的身高 与其影子长 正好相等,接着李明沿 方向继续前进,走到点 处时,李明直立时的影子恰好是线段 ,并测得 ,已知李明直立时的身高为 .求路灯 的高.(结果精确到 )
13. 某校数学兴趣小组为了测量一个池塘 , 两端的距离,设计了如下几种方案:
①如图①,先在平地上取一个可直接到达 , 的点 ,再连接 ,,并分别延长 至点 , 至点 ,使 ,,最后测出 的长度即为 , 间的距离.
②如图②,先过 点作 的垂线 ,再在 上取 , 两点,使 ,接着过点 作 的垂线 ,交 的延长线于点 ,则所测出的 的长即为 , 间的距离.
(1)方案①是否可行 答: .理由是 .
(2)方案②是否可行 答: .理由是 .
(3)方案②中作 , 的目的是使 .
(4)方案②中,若使 ,能否测出(或求出) 的长 理由是什么 若 ,求出 的长.
14. 如图所示,甲、乙两个工厂在一条河的同侧,它们到河边的距离分别为 和 ,两厂水平方向的距离为 ,现要在河边建一个码头,码头到两厂之间修通公路,要使公路最短,码头应建在哪里
答案
第一部分
1. B
2. B
第二部分
3.
【解析】,,
.
是 的外角,
.
.
.
4.
5.
【解析】由题意知 ,解得 .
6.
【解析】由题意知 ,
,
(里).
7.
【解析】设旗杆的高度为 ,则 ,解得 .
8.
第三部分
9. 过点 作 ,交 于 ,交 于 ,过点 作 于点 ,则 ,设垂足为 .
则 ,
.
由题意知 ,.
,
.
,
即 ,
解得 .
,
即横梁 的长为 .
10. 过 作 ,如图.
,
.
又 ,
,
.
又 ,,.
.
地下停车场应该限高 .
11. (1) 由题意知 ,
所以 ,
所以 .
在 中,,
而 ,,
所以 .
(2) 由()知 ,王刚到达 处所用的时间为 .
张华到达 处所用时间为 .
所以张华追赶王刚的速度为 .
12. 设 的高为 .
,,,
,.
,
.
由 得 ,
,即 ,解得 .
路灯 的高约为 .
13. (1) 可行;由 ,得
(2) 可行;由 ,得
(3)
(4) 能.
理由:
,
,
,
而 ,即 ,
.
若 ,则 .
14. 如图,延长 到 ,使 ,连接 交 于点 ,
则码头应建在点 处.
设 ,则 .
,,
,
,即 ,解得 ,即 .
故码头应建在距 点 的点 处.
第1页(共1 页)
