建宁中学五步分层教学法学案--位似图形
文档属性
| 名称 | 建宁中学五步分层教学法学案--位似图形 | 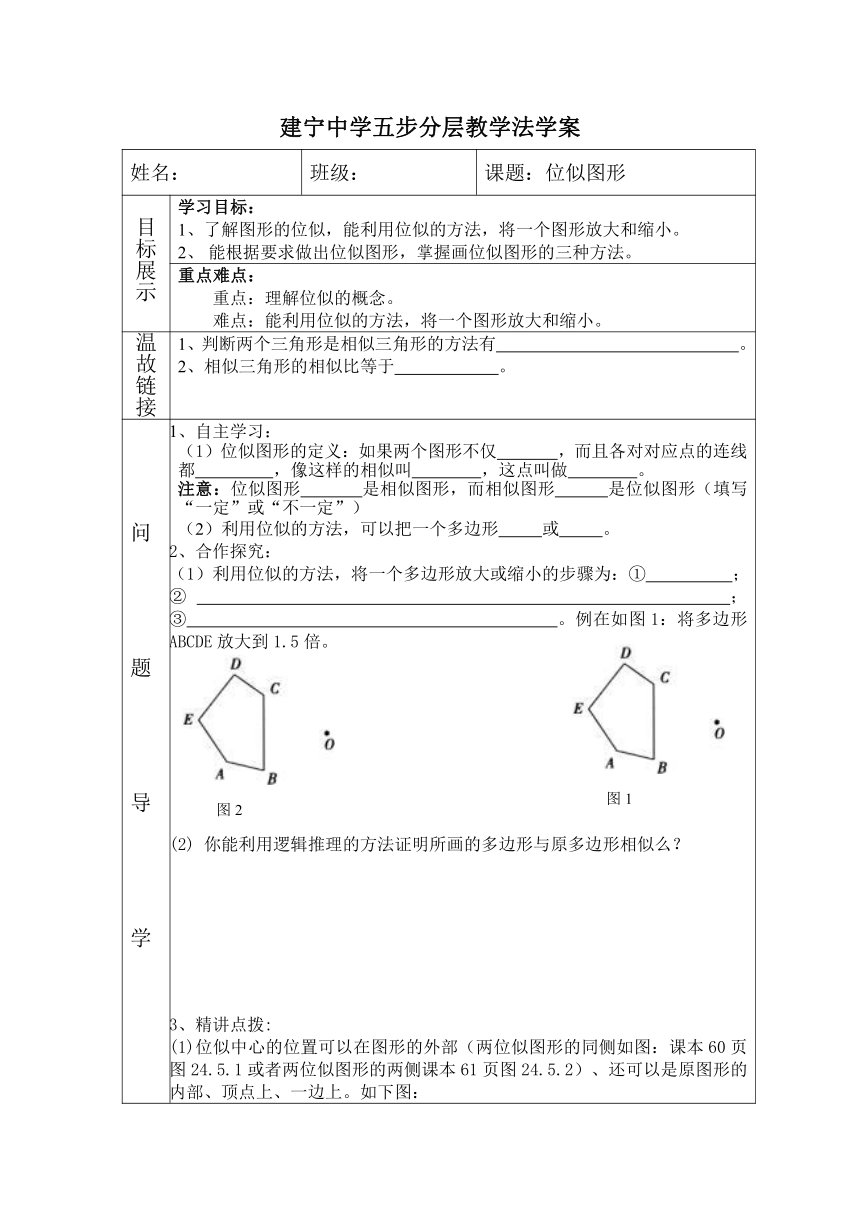 | |
| 格式 | zip | ||
| 文件大小 | 82.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-18 12:40:50 | ||
图片预览

文档简介
建宁中学五步分层教学法学案
姓名:
班级:
课题:位似图形
目
标
展
示
学习目标:
1、了解图形的位似,能利用位似的方法,将一个图形放大和缩小。
2、 能根据要求做出位似图形,掌握画位似图形的三种方法。
重点难点:
重点:理解位似的概念。
难点:能利用位似的方法,将一个图形放大和缩小。
温故链接
1、判断两个三角形是相似三角形的方法有 。
2、相似三角形的相似比等于 。
问
题
导
学
自主学习:
(1)位似图形的定义:如果两个图形不仅 ,而且各对对应点的连线都 ,像这样的相似叫 ,这点叫做 。
注意:位似图形 是相似图形,而相似图形 是位似图形(填写“一定”或“不一定”)
(2)利用位似的方法,可以把一个多边形 或 。
2、合作探究:
(1)利用位似的方法,将一个多边形放大或缩小的步骤为:① ;② ;③ 。例在如图1:将多边形ABCDE放大到1.5倍。
(2) 你能利用逻辑推理的方法证明所画的多边形与原多边形相似么?
3、精讲点拨:
(1)位似中心的位置可以在图形的外部(两位似图形的同侧如图:课本60页图24.5.1或者两位似图形的两侧课本61页图24.5.2)、还可以是原图形的内部、顶点上、一边上。如下图:
(2)位似图形与中心对称图形的联系与区别:
联系:对应点的连线交于一点,对应边 ,对应角 。
区别:位似图形的对应边 ,位似图形的对应点的连线不一定是 。
巩
固
训
练
1、基础达标:
(1)下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等;
B.两个图形如果是位似图形,那么这两个图形不一定相似;
C、两个图形如果是相似图形,那么这两个图形一定位似;
D、两个图形如果是位似图形,那么这两个图形一定相似。
(2)、如果四边形ABCD的位似图形为四边形 A′B′C′D′,且O为位似中心,则下列说法中,正确的是( )
A、O一定在四边形ABCD外 ; B、O不能在四边形ABCD上;
C、若OA:O A′=1:2,则可得到放大两倍的位似形;
D、O在四边形ABCD外时,只能得到放大的位似形;
(3)如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A. B. C. D.
2、能力提升:
(1)如图所示,请你找出这对位似图形的位似中心点O的位置。
(2) 任选一种方法,按下列相似比画出一个三角形的位似图形。
①相似比为0.5 ②相似比为2.5
课后反思
本节课你的收获是: 。
你的疑点是: 。
姓名:
班级:
课题:位似图形
目
标
展
示
学习目标:
1、了解图形的位似,能利用位似的方法,将一个图形放大和缩小。
2、 能根据要求做出位似图形,掌握画位似图形的三种方法。
重点难点:
重点:理解位似的概念。
难点:能利用位似的方法,将一个图形放大和缩小。
温故链接
1、判断两个三角形是相似三角形的方法有 。
2、相似三角形的相似比等于 。
问
题
导
学
自主学习:
(1)位似图形的定义:如果两个图形不仅 ,而且各对对应点的连线都 ,像这样的相似叫 ,这点叫做 。
注意:位似图形 是相似图形,而相似图形 是位似图形(填写“一定”或“不一定”)
(2)利用位似的方法,可以把一个多边形 或 。
2、合作探究:
(1)利用位似的方法,将一个多边形放大或缩小的步骤为:① ;② ;③ 。例在如图1:将多边形ABCDE放大到1.5倍。
(2) 你能利用逻辑推理的方法证明所画的多边形与原多边形相似么?
3、精讲点拨:
(1)位似中心的位置可以在图形的外部(两位似图形的同侧如图:课本60页图24.5.1或者两位似图形的两侧课本61页图24.5.2)、还可以是原图形的内部、顶点上、一边上。如下图:
(2)位似图形与中心对称图形的联系与区别:
联系:对应点的连线交于一点,对应边 ,对应角 。
区别:位似图形的对应边 ,位似图形的对应点的连线不一定是 。
巩
固
训
练
1、基础达标:
(1)下列说法正确的是( )
A.两个图形如果是位似图形,那么这两个图形一定全等;
B.两个图形如果是位似图形,那么这两个图形不一定相似;
C、两个图形如果是相似图形,那么这两个图形一定位似;
D、两个图形如果是位似图形,那么这两个图形一定相似。
(2)、如果四边形ABCD的位似图形为四边形 A′B′C′D′,且O为位似中心,则下列说法中,正确的是( )
A、O一定在四边形ABCD外 ; B、O不能在四边形ABCD上;
C、若OA:O A′=1:2,则可得到放大两倍的位似形;
D、O在四边形ABCD外时,只能得到放大的位似形;
(3)如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心,D,E,F分别是OA,OB,OC的中点,则△DEF与△ABC的面积比是( )
A. B. C. D.
2、能力提升:
(1)如图所示,请你找出这对位似图形的位似中心点O的位置。
(2) 任选一种方法,按下列相似比画出一个三角形的位似图形。
①相似比为0.5 ②相似比为2.5
课后反思
本节课你的收获是: 。
你的疑点是: 。
