建宁中学五步分层教学法学案--梯形的中位线
文档属性
| 名称 | 建宁中学五步分层教学法学案--梯形的中位线 |
|
|
| 格式 | zip | ||
| 文件大小 | 311.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-18 00:00:00 | ||
图片预览

文档简介
建宁中学五步分层教学法学案
姓名:
班级:
课题:梯形的中位线
目
标
展
示
学习目标:在经历观察、操作、探索三角形中位线及重心的基础上,进一步掌握梯形中位线的定义和性质的推理过程。
重点难点:
重点:梯形的中位线性质。
难点:灵活运用梯形的中位线定理解题。
温故链接
1、三角形的中位线是 。
2、三角形的中位线的性质是 。
3、解决有关梯形的问题常做的辅助线有 、 、 。
问
题
导
学
自主学习:
(1)仿照三角形的中位线定义写出梯形的中位线定义:
。
(2)由三角形的中位线的性质定理猜想梯形的中位线的性质定理:
。
2、合作探究:
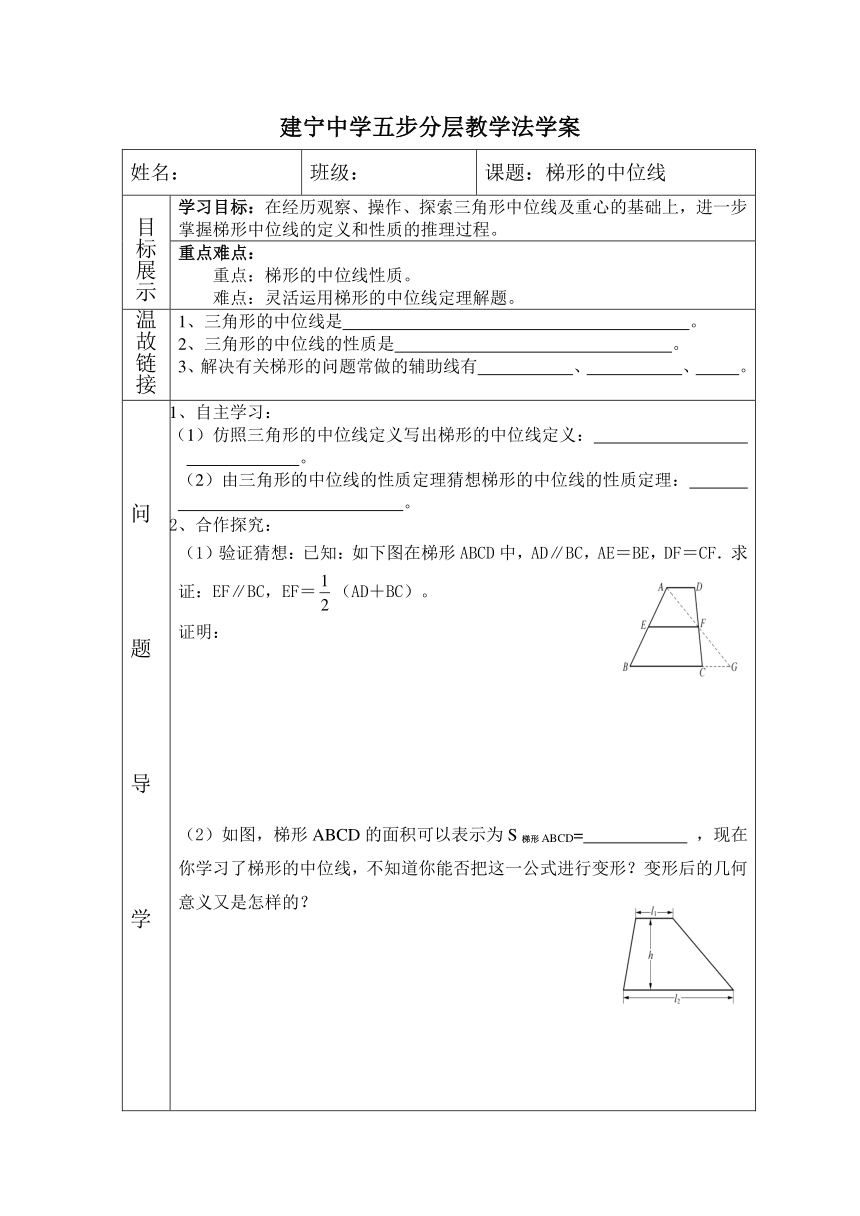
(1)验证猜想:已知:如下图在梯形ABCD中,AD∥BC,AE=BE,DF=CF.求证:EF∥BC,EF=(AD+BC)。
证明:
(2)如图,梯形ABCD的面积可以表示为S梯形ABCD= ,现在你学习了梯形的中位线,不知道你能否把这一公式进行变形?变形后的几何意义又是怎样的?
巩
固
训
练
基础达标:
(1)梯形的中位线长为12cm,上、下底的比是1∶3,那么梯形下底与上底之和是_________;梯形下底与上底之差是_____ 。
(2)如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=0.5m,EE′=0.8m.求BB′、
CC′、DD′的长。
(3)如图所示,直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB的长为b,则图中阴影部分的面积等于________。
(4)如图:DE是△ABC的中位线,F、G分别是BD、CE的中点,如果DE=6,那么FG的长是 。
能力提升:
(1)如图:在△ABC中,BC>AC, 点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF。
①求证:EF∥BC。
②若四边形BDFE的面积为6,求△ABD的面积。
(2)如图:等腰梯形ABCD中,AD∥BC ,点E是线段AD上一个动点(点E与A、D不重合),G、F、H分别是BE、BC、CE的中点。
①试探索四边形EGFH的形状,并说明理由。
②当点E运动到什么位置时,四边形EGFH是菱形?并加以证明。
姓名:
班级:
课题:梯形的中位线
目
标
展
示
学习目标:在经历观察、操作、探索三角形中位线及重心的基础上,进一步掌握梯形中位线的定义和性质的推理过程。
重点难点:
重点:梯形的中位线性质。
难点:灵活运用梯形的中位线定理解题。
温故链接
1、三角形的中位线是 。
2、三角形的中位线的性质是 。
3、解决有关梯形的问题常做的辅助线有 、 、 。
问
题
导
学
自主学习:
(1)仿照三角形的中位线定义写出梯形的中位线定义:
。
(2)由三角形的中位线的性质定理猜想梯形的中位线的性质定理:
。
2、合作探究:
(1)验证猜想:已知:如下图在梯形ABCD中,AD∥BC,AE=BE,DF=CF.求证:EF∥BC,EF=(AD+BC)。
证明:
(2)如图,梯形ABCD的面积可以表示为S梯形ABCD= ,现在你学习了梯形的中位线,不知道你能否把这一公式进行变形?变形后的几何意义又是怎样的?
巩
固
训
练
基础达标:
(1)梯形的中位线长为12cm,上、下底的比是1∶3,那么梯形下底与上底之和是_________;梯形下底与上底之差是_____ 。
(2)如图所示的梯形梯子,AA′∥EE′,AB=BC=CD=DE,A′B′=B′C′=C′D′=D′E′,AA′=0.5m,EE′=0.8m.求BB′、
CC′、DD′的长。
(3)如图所示,直角梯形ABCD的中位线EF的长为a,垂直于底的腰AB的长为b,则图中阴影部分的面积等于________。
(4)如图:DE是△ABC的中位线,F、G分别是BD、CE的中点,如果DE=6,那么FG的长是 。
能力提升:
(1)如图:在△ABC中,BC>AC, 点D在BC上,且DC=AC,∠ACB的平分线CF交AD于F,点E是AB的中点,连结EF。
①求证:EF∥BC。
②若四边形BDFE的面积为6,求△ABD的面积。
(2)如图:等腰梯形ABCD中,AD∥BC ,点E是线段AD上一个动点(点E与A、D不重合),G、F、H分别是BE、BC、CE的中点。
①试探索四边形EGFH的形状,并说明理由。
②当点E运动到什么位置时,四边形EGFH是菱形?并加以证明。
