2021-2022学年山东省济宁市高新区七年级(上)期末数学试卷(五四学制)(Word版含解析)
文档属性
| 名称 | 2021-2022学年山东省济宁市高新区七年级(上)期末数学试卷(五四学制)(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 738.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-21 16:27:44 | ||
图片预览




文档简介
2021-2022学年山东省济宁市高新区七年级第一学期期末数学试卷(五四学制)
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图形中,不是轴对称图形的为( )
A. B.
C. D.
2.的平方根是( )
A.﹣ B. C. D.
3.下列长度的三条线段能组成三角形的是( )
A.3,6,9 B.5,6,8 C.1,2,4 D.5,6,15
4.已知函数y=(m﹣2)+1是一次函数,则m的值为( )
A.± B. C.±2 D.﹣2
5.一次函数y=kx+b的图象如图所示,则点(k,﹣b)在第( )象限内.
A.一 B.二 C.三 D.四
6.已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
7.点P(m+3,m﹣1)在y轴上,则点P的坐标为( )
A.(0,﹣4) B.(5,0) C.(0,5) D.(﹣4,0)
8.如图,以Rt△ABC的三边为直径分别向外作半圆,若斜边AB=3,则图中阴影部分的面积为( )
A.9π B. C. D.3π
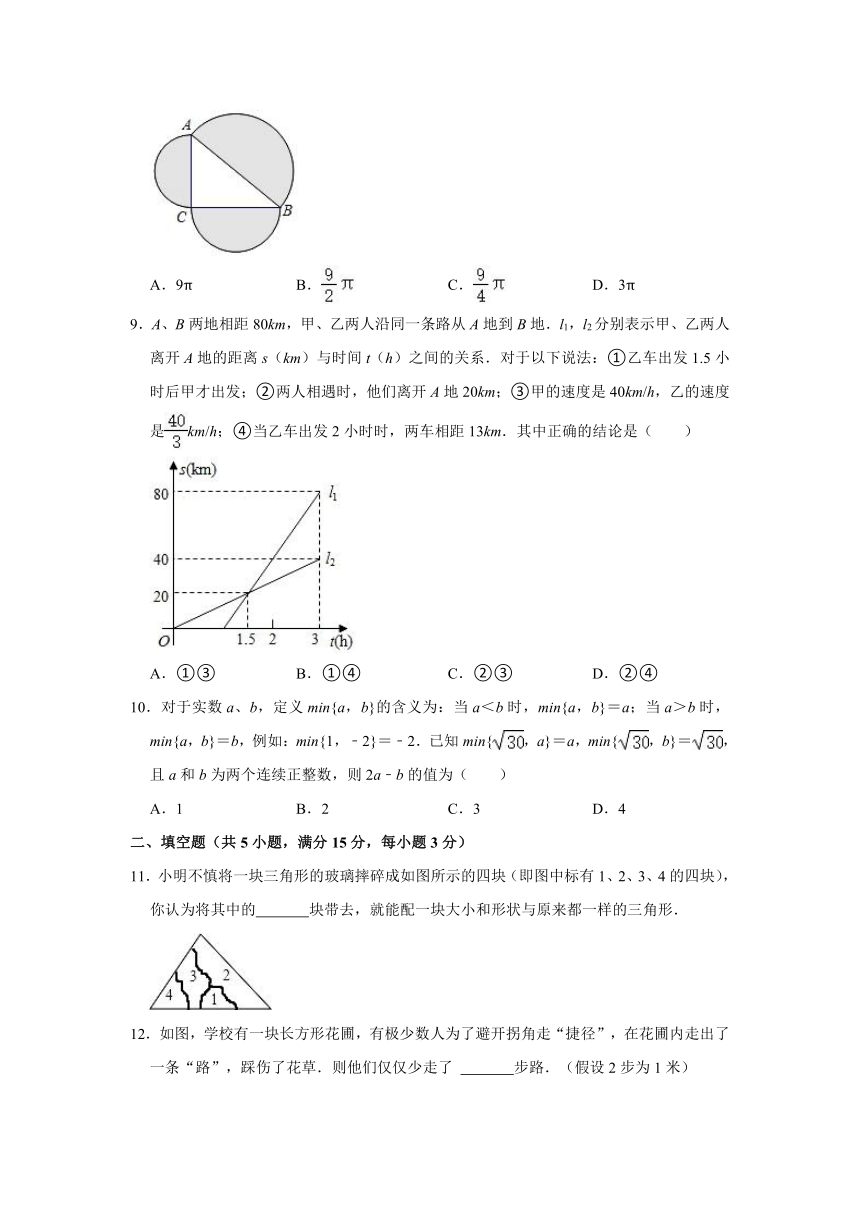
9.A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论是( )
A.①③ B.①④ C.②③ D.②④
10.对于实数a、b,定义min{a,b}的含义为:当a<b时,min{a,b}=a;当a>b时,min{a,b}=b,例如:min{1,﹣2}=﹣2.已知min{,a}=a,min{,b}=,且a和b为两个连续正整数,则2a﹣b的值为( )
A.1 B.2 C.3 D.4
二、填空题(共5小题,满分15分,每小题3分)
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的 块带去,就能配一块大小和形状与原来都一样的三角形.
12.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草.则他们仅仅少走了 步路.(假设2步为1米)
13.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为 .
14.已知a是的整数部分,b是它的小数部分,则(﹣a)3+(b+3)2= .
15.将一次函数y=3x+2的图象进行上下平移,使得平移之后的图象经过点A(4,3),则平移之后图象的解析式为 .
三、解答题(共7小题,满分55分)
16.计算:
(1);
(2).
17.已知x+1的平方根是±2,2x+y﹣2的立方根是2,求x2+y2的算术平方根.
18.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,DE⊥AB于点F,且AB=DE.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
19.一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.
(1)这架云梯的底端距墙角有多远?
(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?
20.如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A2.
(2)求使△APO为等腰三角形的点P的坐标.
21.某电信公司手机通讯有两种收费方式:(A)计时制:0.5元/min;(B)包月制:月租12元,另外通话费按0.2元/min.
(1)写出两种方式每月应缴费用y(元)与通话时间x(min)之间的关系式.
(2)某手机用户平均每个月通话时间为60min,他采用哪种方式较合算?为什么?
(3)如果该用户本月预缴了100元的话费,按包月制算,该用户本月可通话多长时间?
22.如图,已知直线y=﹣x+3与x轴、y轴分别相交于点A、B,将△AOB沿直线CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)过点B作直线BP与x轴交于点P,且使OP=OA,求△ABP的面积.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图形中,不是轴对称图形的为( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:选项A、B、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项C不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:C.
2.的平方根是( )
A.﹣ B. C. D.
【分析】先根据乘方的定义得出(﹣)2=,再利用平方根的概念求解可得.
解:∵(﹣)2=,
∴的平方根是,
故选:C.
3.下列长度的三条线段能组成三角形的是( )
A.3,6,9 B.5,6,8 C.1,2,4 D.5,6,15
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
解:根据三角形的三边关系,得
A、3+6=9,不能组成三角形,不符合题意;
B、6+5=11>8,能组成三角形,符合题意;
C、1+2=3<4,不能够组成三角形,不符合题意;
D、5+6=11<15,不能够组成三角形,不符合题意.
故选:B.
4.已知函数y=(m﹣2)+1是一次函数,则m的值为( )
A.± B. C.±2 D.﹣2
【分析】根据一次函数的定义,自变量的次数为1列方程求出m的值,再根据比例系数k≠0求解得到m≠2,从而得解.
解:由题意得,m2﹣3=1且m﹣2≠0,
解得m=±2且m≠2,
所以m=﹣2.
故选:D.
5.一次函数y=kx+b的图象如图所示,则点(k,﹣b)在第( )象限内.
A.一 B.二 C.三 D.四
【分析】根据一次函数图象的位置确定出k与b的正负,即可作出判断.
解:根据数轴上直线的位置得:k<0,b<0,
∴﹣b>0,
则以k、﹣b为坐标的点(k,﹣b)在第二象限内.
故选:B.
6.已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
【分析】根据一次函数y=3x+a的一次项系数k>0时,函数值随自变量的增大而增大的性质来求解即可.
解:∵一次函数y=3x+a的一次项系数为3>0,
∴y随x的增大而增大,
∵点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,﹣1<4,
∴y1<y2,
故选:A.
7.点P(m+3,m﹣1)在y轴上,则点P的坐标为( )
A.(0,﹣4) B.(5,0) C.(0,5) D.(﹣4,0)
【分析】根据y轴上点的横坐标等于零,可得关于m的方程,解方程可得m的值,根据m的值,可得点的坐标.
解:点P(m+3,m﹣1)在y轴上,得:
m+3=0.
解得m=﹣3,
m﹣1=﹣4,
点P的坐标是(0,﹣4),
故选:A.
8.如图,以Rt△ABC的三边为直径分别向外作半圆,若斜边AB=3,则图中阴影部分的面积为( )
A.9π B. C. D.3π
【分析】利用勾股定理和圆的面积公式解答.
解:根据题意知:AC2+BC2=AB2=9.
图中阴影部分的面积=π×(AC)2+π×(BC)2+π×(AB)2
=π(AC2+BC2+AB2)
=π×(9+9)
=.
故选:C.
9.A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论是( )
A.①③ B.①④ C.②③ D.②④
【分析】根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,从而可以解答本题.
解:由图可得,
乙车出发1.5小时后甲已经出发一段时间,故①错误;
两人相遇时,他们离开A地20km,故②正确;
甲的速度是(80﹣20)÷(3﹣1.5)=40(km/h),乙的速度是40÷3=(km/h),故③正确;
当乙车出发2小时时,两车相距:[20+40×(2﹣1.5)]﹣×2=(km),故④错误;
故选:C.
10.对于实数a、b,定义min{a,b}的含义为:当a<b时,min{a,b}=a;当a>b时,min{a,b}=b,例如:min{1,﹣2}=﹣2.已知min{,a}=a,min{,b}=,且a和b为两个连续正整数,则2a﹣b的值为( )
A.1 B.2 C.3 D.4
【分析】根据a,b的范围,然后再代入求出2a﹣b的值即可.
解:∵min{,a}=a,min{,b}=.
∴a<,b>.
∵a,b是两个连续的正整数.
∴a=5,b=6.
∴2a﹣b=2×5﹣6=4.
故选:D.
二、填空题(共5小题,满分15分,每小题3分)
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的 2 块带去,就能配一块大小和形状与原来都一样的三角形.
【分析】应先假定选择哪块,再对应三角形全等判定的条件进行验证.
解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故答案为:2.
12.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草.则他们仅仅少走了 8 步路.(假设2步为1米)
【分析】在Rt△ABC中,利用勾股定理求出AB的长,根据2步为1米,即可得出少走的步数.
解:∵∠C=90°,AC=6m,BC=8m,
∴AB==10(m),
则(8+6﹣10)×2=8,
∴他们仅仅少走了8步,
故答案为:8.
13.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为 18 .
【分析】根据线段的垂直平分线的性质得到EA=EC,根据三角形的周长公式计算即可.
解:∵DE是△ABC中AC边的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18,
故答案为:18.
14.已知a是的整数部分,b是它的小数部分,则(﹣a)3+(b+3)2= ﹣17 .
【分析】由于3<<4,由此可得的整数部分和小数部分,再进一步代入求得数值即可.
解:∵3<<4,
∴的整数部分=3,小数部分为 ﹣3,
则(﹣a)3+(b+3)2=(﹣3)3+(﹣3+3)2=﹣27+10=﹣17.
故答案为:﹣17.
15.将一次函数y=3x+2的图象进行上下平移,使得平移之后的图象经过点A(4,3),则平移之后图象的解析式为 y=3x﹣9 .
【分析】平移时k的值不变,只有b发生变化.
解:新直线是由一次函数y=3x+2的图象平移得到的,
∴新直线的k=3.可设新直线的解析式为:y=3x+b.
∵经过点(4,3),则3×4+b=3.
解得b=﹣9.
∴平移后图象函数的解析式为y=3x﹣9.
故答案是:y=3x﹣9.
三、解答题(共7小题,满分55分)
16.计算:
(1);
(2).
【分析】(1)直接利用二次根式的性质以及立方根的性质、有理数的乘方运算法则分别化简,进而利用有理数的加减运算法则计算得出答案;
(2)直接利用二次根式的性质以及立方根的性质、绝对值的性质分别化简,进而利用实数的加减运算法则计算得出答案.
解:(1)原式=5﹣4+1
=2;
(2)原式=
=.
17.已知x+1的平方根是±2,2x+y﹣2的立方根是2,求x2+y2的算术平方根.
【分析】根据平方根、立方根的定义即可得到x、y的值,最后代入代数式求解即可.
解:∵x+1的平方根是±2,
∴x+1=4,
∴x=3,
∵2x+y﹣2的立方根是2,
∴2x+y﹣2=8,
把x的值代入解得:
y=4,
∴x2+y2=25,
∴x2+y2的算术平方根为5.
18.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,DE⊥AB于点F,且AB=DE.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
【分析】(1)由“AAS”可证△ACB≌△EBD;
(2)由全等三角形的性质可得BC=DB=12,AC=EB,即可求解.
【解答】(1)证明:∵∠ACB=∠DBC=90°,DE⊥AB,
∴∠DEB+∠ABC=90°,∠A+∠ABC=90°,
∴∠DEB=∠A,
在△ACB和△EBD中,
,
∴△ACB≌△EBD(AAS);
(2)解:∵△ACB≌△EBD,
∴BC=DB,AC=EB,
∵E是BC的中点,
∴,
∵DB=12,BC=DB,
∴BC=12,
∴AC=EB=BC=6.
19.一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.
(1)这架云梯的底端距墙角有多远?
(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?
【分析】(1)在RtADE中,利用勾股定理即可求出DE的长;
(2)首先求出A′E的长,利用勾股定理可求出D′E的长,进而得到DD′=ED′﹣ED的值.
解:(1)在Rt△ADE中,由勾股定理得AE2+DE2=AD2,
即DE2+242=252,
∴DE==7(m),
答:这架云梯的底端距墙角有7 m远;
(2)∵云梯的顶端A下滑了4m至点A′,
∴A′E=AE﹣AA′=24﹣4=20(m),
在Rt△A′ED′中,由勾股定理得A′E2+D′E2=A′D′2,
即202+D′E2=252,
∴D′E==15(m),
∴DD′=ED′﹣ED=15﹣7=8(m),
答:梯子的底端在水平方向也滑动了8m.
20.如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A2.
(2)求使△APO为等腰三角形的点P的坐标.
【分析】(1)利用关于原点对称和y轴对称的点的坐标特征写出点A1,A2的坐标,然后描点;
(2)先计算出OA的长,再分类讨论:当OP=OA或AP=AO或PO=PA时,利用直角坐标系分别写出对应的P点坐标.
解:(1)A1(﹣2,2),A1(﹣2,﹣2),如图,
(2)设P点坐标为(t,0),
OA==2,
当OP=OA时,P点坐标为(﹣2,0)或(2,0);
当AP=AO时,P点坐标为(4,0),
当PO=PA时,P点坐标为(2,0),
综上所述,P点坐标为(﹣2,0)或(2,0)或(4,0)或(2,0).
21.某电信公司手机通讯有两种收费方式:(A)计时制:0.5元/min;(B)包月制:月租12元,另外通话费按0.2元/min.
(1)写出两种方式每月应缴费用y(元)与通话时间x(min)之间的关系式.
(2)某手机用户平均每个月通话时间为60min,他采用哪种方式较合算?为什么?
(3)如果该用户本月预缴了100元的话费,按包月制算,该用户本月可通话多长时间?
【分析】(1)根据收费标准写出函数关系式;
(2)将x=60代入(1)中的两个函数关系式,求出相应的函数值,然后比较大小即可;
(3)在解析式中令y=100,求得x即可.
解:(1)由题意可得,
计时制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.5x,
包月制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.2x+12;
(2)包月制收费方式比较合算,理由如下:
当x=60时,
计时制:每月应缴费用为:0.5×60=30(元),
包月制:每月应缴费用为:0.2×60+12=24(元),
∵30>24,
∴包月制收费方式比较合算;
(3)当y=100时,0.2x+12=100,
解得x=440.
答:该用户本月可通话440min.
22.如图,已知直线y=﹣x+3与x轴、y轴分别相交于点A、B,将△AOB沿直线CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 (4,0) ,点B的坐标为 (0,3) ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)过点B作直线BP与x轴交于点P,且使OP=OA,求△ABP的面积.
【分析】(1)令x=0和y=0即可求出点A,B的坐标;
(2)连接BC,设OC=x,则AC=BC=4﹣x,在Rt△BOC中,利用勾股定理求出x,再利用待定系数法求出直线BC的解析式即可;
(3)先求出点P的坐标,根据三角形的面积公式即可求解.
解:(1)令y=0,则x=4;令x=0,则y=3,
故点A的坐标为(4,0),点B的坐标为(0,3).
故答案为:(4,0),(0,3);
(2)连接BC,
设OC=x,
∵直线CD垂直平分线段AB,
∴AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得x=,
∴OC=,
∴C(,0),
设直线BC的解析式为y=kx+b,
则有,
解得,
∴直线BC的解析式为y=﹣x+3;
(3)如图,
∵点A的坐标为(4,0),
∴OA=4,
∵OP=OA,
∴OP=2,
∴点P的坐标为(2,0),P′(﹣2,0),
∴AP=2,AP′=6,
∴S△ABP=AP OB=×2×3=3;
S△ABP′=AP′ OB=×6×3=9.
综上:△ABP的面积为3或9.
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图形中,不是轴对称图形的为( )
A. B.
C. D.
2.的平方根是( )
A.﹣ B. C. D.
3.下列长度的三条线段能组成三角形的是( )
A.3,6,9 B.5,6,8 C.1,2,4 D.5,6,15
4.已知函数y=(m﹣2)+1是一次函数,则m的值为( )
A.± B. C.±2 D.﹣2
5.一次函数y=kx+b的图象如图所示,则点(k,﹣b)在第( )象限内.
A.一 B.二 C.三 D.四
6.已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
7.点P(m+3,m﹣1)在y轴上,则点P的坐标为( )
A.(0,﹣4) B.(5,0) C.(0,5) D.(﹣4,0)
8.如图,以Rt△ABC的三边为直径分别向外作半圆,若斜边AB=3,则图中阴影部分的面积为( )
A.9π B. C. D.3π
9.A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论是( )
A.①③ B.①④ C.②③ D.②④
10.对于实数a、b,定义min{a,b}的含义为:当a<b时,min{a,b}=a;当a>b时,min{a,b}=b,例如:min{1,﹣2}=﹣2.已知min{,a}=a,min{,b}=,且a和b为两个连续正整数,则2a﹣b的值为( )
A.1 B.2 C.3 D.4
二、填空题(共5小题,满分15分,每小题3分)
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的 块带去,就能配一块大小和形状与原来都一样的三角形.
12.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草.则他们仅仅少走了 步路.(假设2步为1米)
13.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为 .
14.已知a是的整数部分,b是它的小数部分,则(﹣a)3+(b+3)2= .
15.将一次函数y=3x+2的图象进行上下平移,使得平移之后的图象经过点A(4,3),则平移之后图象的解析式为 .
三、解答题(共7小题,满分55分)
16.计算:
(1);
(2).
17.已知x+1的平方根是±2,2x+y﹣2的立方根是2,求x2+y2的算术平方根.
18.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,DE⊥AB于点F,且AB=DE.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
19.一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.
(1)这架云梯的底端距墙角有多远?
(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?
20.如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A2.
(2)求使△APO为等腰三角形的点P的坐标.
21.某电信公司手机通讯有两种收费方式:(A)计时制:0.5元/min;(B)包月制:月租12元,另外通话费按0.2元/min.
(1)写出两种方式每月应缴费用y(元)与通话时间x(min)之间的关系式.
(2)某手机用户平均每个月通话时间为60min,他采用哪种方式较合算?为什么?
(3)如果该用户本月预缴了100元的话费,按包月制算,该用户本月可通话多长时间?
22.如图,已知直线y=﹣x+3与x轴、y轴分别相交于点A、B,将△AOB沿直线CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 ,点B的坐标为 ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)过点B作直线BP与x轴交于点P,且使OP=OA,求△ABP的面积.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.下列四个图形中,不是轴对称图形的为( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
解:选项A、B、D能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项C不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:C.
2.的平方根是( )
A.﹣ B. C. D.
【分析】先根据乘方的定义得出(﹣)2=,再利用平方根的概念求解可得.
解:∵(﹣)2=,
∴的平方根是,
故选:C.
3.下列长度的三条线段能组成三角形的是( )
A.3,6,9 B.5,6,8 C.1,2,4 D.5,6,15
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,进行分析.
解:根据三角形的三边关系,得
A、3+6=9,不能组成三角形,不符合题意;
B、6+5=11>8,能组成三角形,符合题意;
C、1+2=3<4,不能够组成三角形,不符合题意;
D、5+6=11<15,不能够组成三角形,不符合题意.
故选:B.
4.已知函数y=(m﹣2)+1是一次函数,则m的值为( )
A.± B. C.±2 D.﹣2
【分析】根据一次函数的定义,自变量的次数为1列方程求出m的值,再根据比例系数k≠0求解得到m≠2,从而得解.
解:由题意得,m2﹣3=1且m﹣2≠0,
解得m=±2且m≠2,
所以m=﹣2.
故选:D.
5.一次函数y=kx+b的图象如图所示,则点(k,﹣b)在第( )象限内.
A.一 B.二 C.三 D.四
【分析】根据一次函数图象的位置确定出k与b的正负,即可作出判断.
解:根据数轴上直线的位置得:k<0,b<0,
∴﹣b>0,
则以k、﹣b为坐标的点(k,﹣b)在第二象限内.
故选:B.
6.已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
【分析】根据一次函数y=3x+a的一次项系数k>0时,函数值随自变量的增大而增大的性质来求解即可.
解:∵一次函数y=3x+a的一次项系数为3>0,
∴y随x的增大而增大,
∵点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,﹣1<4,
∴y1<y2,
故选:A.
7.点P(m+3,m﹣1)在y轴上,则点P的坐标为( )
A.(0,﹣4) B.(5,0) C.(0,5) D.(﹣4,0)
【分析】根据y轴上点的横坐标等于零,可得关于m的方程,解方程可得m的值,根据m的值,可得点的坐标.
解:点P(m+3,m﹣1)在y轴上,得:
m+3=0.
解得m=﹣3,
m﹣1=﹣4,
点P的坐标是(0,﹣4),
故选:A.
8.如图,以Rt△ABC的三边为直径分别向外作半圆,若斜边AB=3,则图中阴影部分的面积为( )
A.9π B. C. D.3π
【分析】利用勾股定理和圆的面积公式解答.
解:根据题意知:AC2+BC2=AB2=9.
图中阴影部分的面积=π×(AC)2+π×(BC)2+π×(AB)2
=π(AC2+BC2+AB2)
=π×(9+9)
=.
故选:C.
9.A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论是( )
A.①③ B.①④ C.②③ D.②④
【分析】根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,从而可以解答本题.
解:由图可得,
乙车出发1.5小时后甲已经出发一段时间,故①错误;
两人相遇时,他们离开A地20km,故②正确;
甲的速度是(80﹣20)÷(3﹣1.5)=40(km/h),乙的速度是40÷3=(km/h),故③正确;
当乙车出发2小时时,两车相距:[20+40×(2﹣1.5)]﹣×2=(km),故④错误;
故选:C.
10.对于实数a、b,定义min{a,b}的含义为:当a<b时,min{a,b}=a;当a>b时,min{a,b}=b,例如:min{1,﹣2}=﹣2.已知min{,a}=a,min{,b}=,且a和b为两个连续正整数,则2a﹣b的值为( )
A.1 B.2 C.3 D.4
【分析】根据a,b的范围,然后再代入求出2a﹣b的值即可.
解:∵min{,a}=a,min{,b}=.
∴a<,b>.
∵a,b是两个连续的正整数.
∴a=5,b=6.
∴2a﹣b=2×5﹣6=4.
故选:D.
二、填空题(共5小题,满分15分,每小题3分)
11.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的 2 块带去,就能配一块大小和形状与原来都一样的三角形.
【分析】应先假定选择哪块,再对应三角形全等判定的条件进行验证.
解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故答案为:2.
12.如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草.则他们仅仅少走了 8 步路.(假设2步为1米)
【分析】在Rt△ABC中,利用勾股定理求出AB的长,根据2步为1米,即可得出少走的步数.
解:∵∠C=90°,AC=6m,BC=8m,
∴AB==10(m),
则(8+6﹣10)×2=8,
∴他们仅仅少走了8步,
故答案为:8.
13.如图,△ABC中,DE垂直平分边AC,若BC=8,AB=10,则△EBC的周长为 18 .
【分析】根据线段的垂直平分线的性质得到EA=EC,根据三角形的周长公式计算即可.
解:∵DE是△ABC中AC边的垂直平分线,
∴EA=EC,
∴△EBC的周长=BC+BE+EC=BC+BE+EA=BC+BA=18,
故答案为:18.
14.已知a是的整数部分,b是它的小数部分,则(﹣a)3+(b+3)2= ﹣17 .
【分析】由于3<<4,由此可得的整数部分和小数部分,再进一步代入求得数值即可.
解:∵3<<4,
∴的整数部分=3,小数部分为 ﹣3,
则(﹣a)3+(b+3)2=(﹣3)3+(﹣3+3)2=﹣27+10=﹣17.
故答案为:﹣17.
15.将一次函数y=3x+2的图象进行上下平移,使得平移之后的图象经过点A(4,3),则平移之后图象的解析式为 y=3x﹣9 .
【分析】平移时k的值不变,只有b发生变化.
解:新直线是由一次函数y=3x+2的图象平移得到的,
∴新直线的k=3.可设新直线的解析式为:y=3x+b.
∵经过点(4,3),则3×4+b=3.
解得b=﹣9.
∴平移后图象函数的解析式为y=3x﹣9.
故答案是:y=3x﹣9.
三、解答题(共7小题,满分55分)
16.计算:
(1);
(2).
【分析】(1)直接利用二次根式的性质以及立方根的性质、有理数的乘方运算法则分别化简,进而利用有理数的加减运算法则计算得出答案;
(2)直接利用二次根式的性质以及立方根的性质、绝对值的性质分别化简,进而利用实数的加减运算法则计算得出答案.
解:(1)原式=5﹣4+1
=2;
(2)原式=
=.
17.已知x+1的平方根是±2,2x+y﹣2的立方根是2,求x2+y2的算术平方根.
【分析】根据平方根、立方根的定义即可得到x、y的值,最后代入代数式求解即可.
解:∵x+1的平方根是±2,
∴x+1=4,
∴x=3,
∵2x+y﹣2的立方根是2,
∴2x+y﹣2=8,
把x的值代入解得:
y=4,
∴x2+y2=25,
∴x2+y2的算术平方根为5.
18.如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,DE⊥AB于点F,且AB=DE.
(1)求证:△ACB≌△EBD;
(2)若DB=12,求AC的长.
【分析】(1)由“AAS”可证△ACB≌△EBD;
(2)由全等三角形的性质可得BC=DB=12,AC=EB,即可求解.
【解答】(1)证明:∵∠ACB=∠DBC=90°,DE⊥AB,
∴∠DEB+∠ABC=90°,∠A+∠ABC=90°,
∴∠DEB=∠A,
在△ACB和△EBD中,
,
∴△ACB≌△EBD(AAS);
(2)解:∵△ACB≌△EBD,
∴BC=DB,AC=EB,
∵E是BC的中点,
∴,
∵DB=12,BC=DB,
∴BC=12,
∴AC=EB=BC=6.
19.一架云梯长25m,如图那样斜靠在一面墙上,云梯顶端离地面24m.
(1)这架云梯的底端距墙角有多远?
(2)如果云梯的顶端下滑了4m,那么它的底部在水平方向滑动了多少m?
【分析】(1)在RtADE中,利用勾股定理即可求出DE的长;
(2)首先求出A′E的长,利用勾股定理可求出D′E的长,进而得到DD′=ED′﹣ED的值.
解:(1)在Rt△ADE中,由勾股定理得AE2+DE2=AD2,
即DE2+242=252,
∴DE==7(m),
答:这架云梯的底端距墙角有7 m远;
(2)∵云梯的顶端A下滑了4m至点A′,
∴A′E=AE﹣AA′=24﹣4=20(m),
在Rt△A′ED′中,由勾股定理得A′E2+D′E2=A′D′2,
即202+D′E2=252,
∴D′E==15(m),
∴DD′=ED′﹣ED=15﹣7=8(m),
答:梯子的底端在水平方向也滑动了8m.
20.如图,在平面直角坐标系中,已知点A(2,﹣2),点P是x轴上的一个动点.
(1)A1,A2分别是点A关于原点的对称点和关于y轴对称的点,直接写出点A1,A2的坐标,并在图中描出点A1,A2.
(2)求使△APO为等腰三角形的点P的坐标.
【分析】(1)利用关于原点对称和y轴对称的点的坐标特征写出点A1,A2的坐标,然后描点;
(2)先计算出OA的长,再分类讨论:当OP=OA或AP=AO或PO=PA时,利用直角坐标系分别写出对应的P点坐标.
解:(1)A1(﹣2,2),A1(﹣2,﹣2),如图,
(2)设P点坐标为(t,0),
OA==2,
当OP=OA时,P点坐标为(﹣2,0)或(2,0);
当AP=AO时,P点坐标为(4,0),
当PO=PA时,P点坐标为(2,0),
综上所述,P点坐标为(﹣2,0)或(2,0)或(4,0)或(2,0).
21.某电信公司手机通讯有两种收费方式:(A)计时制:0.5元/min;(B)包月制:月租12元,另外通话费按0.2元/min.
(1)写出两种方式每月应缴费用y(元)与通话时间x(min)之间的关系式.
(2)某手机用户平均每个月通话时间为60min,他采用哪种方式较合算?为什么?
(3)如果该用户本月预缴了100元的话费,按包月制算,该用户本月可通话多长时间?
【分析】(1)根据收费标准写出函数关系式;
(2)将x=60代入(1)中的两个函数关系式,求出相应的函数值,然后比较大小即可;
(3)在解析式中令y=100,求得x即可.
解:(1)由题意可得,
计时制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.5x,
包月制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.2x+12;
(2)包月制收费方式比较合算,理由如下:
当x=60时,
计时制:每月应缴费用为:0.5×60=30(元),
包月制:每月应缴费用为:0.2×60+12=24(元),
∵30>24,
∴包月制收费方式比较合算;
(3)当y=100时,0.2x+12=100,
解得x=440.
答:该用户本月可通话440min.
22.如图,已知直线y=﹣x+3与x轴、y轴分别相交于点A、B,将△AOB沿直线CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)点A的坐标为 (4,0) ,点B的坐标为 (0,3) ;
(2)求OC的长度,并求出此时直线BC的表达式;
(3)过点B作直线BP与x轴交于点P,且使OP=OA,求△ABP的面积.
【分析】(1)令x=0和y=0即可求出点A,B的坐标;
(2)连接BC,设OC=x,则AC=BC=4﹣x,在Rt△BOC中,利用勾股定理求出x,再利用待定系数法求出直线BC的解析式即可;
(3)先求出点P的坐标,根据三角形的面积公式即可求解.
解:(1)令y=0,则x=4;令x=0,则y=3,
故点A的坐标为(4,0),点B的坐标为(0,3).
故答案为:(4,0),(0,3);
(2)连接BC,
设OC=x,
∵直线CD垂直平分线段AB,
∴AC=CB=4﹣x,
∵∠BOA=90°,
∴OB2+OC2=CB2,
32+x2=(4﹣x)2,
解得x=,
∴OC=,
∴C(,0),
设直线BC的解析式为y=kx+b,
则有,
解得,
∴直线BC的解析式为y=﹣x+3;
(3)如图,
∵点A的坐标为(4,0),
∴OA=4,
∵OP=OA,
∴OP=2,
∴点P的坐标为(2,0),P′(﹣2,0),
∴AP=2,AP′=6,
∴S△ABP=AP OB=×2×3=3;
S△ABP′=AP′ OB=×6×3=9.
综上:△ABP的面积为3或9.
同课章节目录
